Solved Problems

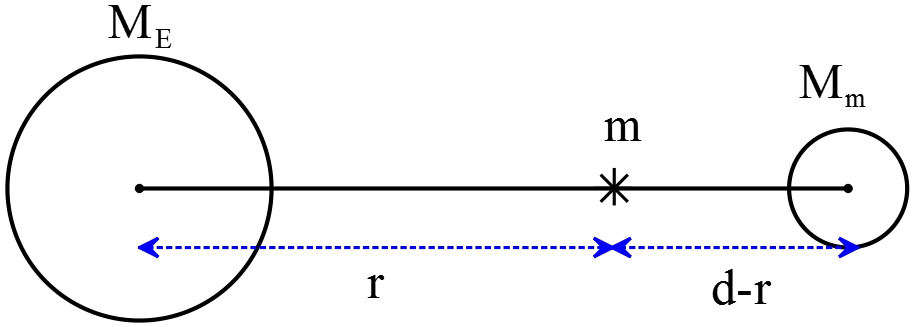
Suppose the desired point to be at distance $r$ from the center of the Earth. Balance gravitational pulls of Earth and the moon on some $m$ placed at this point:
\begin{gather*} G\frac{M_Em}{r^2}=G\frac{M_Mm}{{\left(d-r\right)}^2} \\ \to M_E{\left(d-r\right)}^{2}=M_Mr^{2} \end{gather*} We want to find $r$ in terms of the others. We can rearrange above equation to get the following \[\Big(1-\frac rd \Big)^{2}=\frac{M_M}{M_E}\Big(\frac{r}{d}\Big)^{2}\] Next let $q\equiv \frac{M_M}{M_E}\ ,\ x=\frac{r}{d}$ then we have \begin{gather*} \left(1-x\right)^2=qx^2 \\ \to \left(1-q\right)x^2-2x+1=0 \end{gather*} The above equation is quadratic one, $ax^2+bx+c=0$ with solution \[x=\frac{-a\pm\sqrt{b^2-4ac}}{2a}\]Thus, solution to the above equation is obtained as below \begin{align*} \Rightarrow x_{1,2}&=\frac{2\pm \sqrt{4-4\sqrt{1-q}}}{2\left(1-q\right)} \\ \\ &=\frac{1}{1\pm \sqrt{q}} \end{align*} After substituting, we get the following distances which one is greater than $d$ and the other is greater \[r_{1,2}=\frac{d}{1\pm \sqrt{\frac{M_M}{M_E}}}\]

The gravitational force between satellite and earth provides the centripetal force on the satellite. Therefore, apply Newton's 2${}^{nd}$ law in the radial direction:
\begin{align*} \Sigma F_r&=ma_r \\  F_G &=ma_r \\ G\frac{M_Em}{R^2}&=m\frac{v^2}{R} \\ \Rightarrow R&={\left(\frac{GM_E}{\omega}\right)}^{\frac{1}{3}}\end{align*} 

Recall that in circular motion $v=R\omega=R\frac{2\pi}{T}$, where $T$ is the period of the motion.
For a satellite with period of $24$ hours, the angular velocity is
\begin{gather*} \omega=\frac{2\pi}{T}={\rm \frac{2\pi}{24\,h\times 60\,m \times 60\,s}} \\ \\ \sim \ 7.27\times {10}^{-5}\ \frac{{\rm rad}}{{\rm s}} \end{gather*}
$\Rightarrow R=42150\ {\rm km}$ from center of the Earth.
Since the radius of the earth is about $6400\,{\rm km}$, then the Turksat is about $35750{\rm \ km}$ from the surface of the earth.

Note: an object at a distance $h$ above a planet's surface experiences a gravitational force with the following acceleration \[a_g=G\frac{M}{{\left(R+h\right)}^2}\] which is the consequence of applying newton's second law in the rotational system.

In the above equation, $R$ and $M$ are the planet's radius and mass, respectively. $G$ is the universal gravitational constant. Hence, at the surface level the gravitational acceleration is \begin{align*} a_g&=G\frac{M}{R+h}\\ \\ &=G\frac{M}{R+0}\\ \\ &=22.5\ \end{align*}
Now insert the values to find the $a_g$ at a distance $R$ above the surface.
\begin{align*} a^{'}_g&=G\frac{M}{R+R} \\ \\ &=\frac{1}{2}\left(G\frac{M}{R}\right)\\ \\&=\frac{1}{2}(22.5)\\ \\ &=11.25 \quad {\rm \frac{m}{s^2}}\end{align*} where a prime ($'$) inserted to distinct acceleration at the surface and above the surface.

The gravitational acceleration of an object with mass $M$ at distance $r$ from its center is given by $g=GM/r^2$ so  \begin{align*} g_r &=\frac{1}{10}g_R \\ \\ G\frac{M}{{\left(r+R\right)}^2} &=\frac{1}{10}G\frac{M}{R^2} \\ \\ \Rightarrow 10R^2&={\left(r+R\right)}^2\end{align*} 
Taking the square root of both sides, we obtain two solutions. \begin{align*} \sqrt{10R^2}&=\sqrt{{\left(r+R\right)}^2} \\ \Rightarrow \pm \sqrt{10}R&=r+R \end{align*} Considering both signs and solving for unknown $r$, we get  \[\Rightarrow \left\{ \begin{array}{rcl}+\sqrt{10}R&=&r+R\Rightarrow r=R\left(\sqrt{10}-1\right)=2.16R \\ -\sqrt{10}R&=&r+R\Rightarrow r=-R(\sqrt{10}+1) \end{array}\right.\] The second result is not accepted since $r<0$ !

First, find the gravitational acceleration of the planet, then using the definition of the gravitational acceleration calculate the mass of the planet.

Use the displacement kinematic equation $y=-\frac 12 gt^2 +v_0t+y_0$, and set the initial velocity zero $v_0=0$ since ``the ball is dropped'' means that its initial velocity is zero. Now, solve this equation for $g$, to find its numerical \begin{gather*} y=\frac{1}{2}gt^2+v_0t+y_0\\\\ g=\frac{2y}{t^2}=\frac{2\times 334}{(6.54)^2}=15.61\quad {\rm m/s^2}\end{gather*}
Where we have chosen the initial position of the ball as the base, so $y_0=0$.  

On the other side, the gravitational acceleration is defined as $g=\frac{GM}{R^2}$, where $R$ is the radius of the planet. Solving this for $M$, we will have \begin{align*} M&=\frac{gR^2}{G}\\\\&=\frac{g(1.55R_e)^2}{G}\\\\&=\frac{15.61\times {\left(1.55\times 6.37\times {10}^6\right)}^2}{6.67\times {10}^{-11}}\\\\&=2.28\times{10}^{25}\quad{\rm kg}\end{align*}

The gravitational force between the satellite and the Moon acts as a centripetal force. Recall that in the circular motion we have $F_r=ma_r=mv^2/r$. Therefore, \begin{align*} F_G&=F_r\\\\ \frac{GM_Mm}{r^2}&=\frac{mv^2}{r}\\\\ \Rightarrow v&=\sqrt{\frac{GM_M}{r}}\\\\ &=\sqrt{\frac{GM}{4R_M}}\\\\&=\frac{1}{2}(g_{moon})^{\frac 12}\end{align*}
This was a question on circular motion. For practicing more problems on this topic, read the following:
Uniform circular motion problems

The surface gravity of a planet with mass $M$ and radius $R$ is given by \[a_g=G\frac{M}{R^2}\] And at the height of $h$ above its surface is 
\[a_g=G\frac{M}{{\left(R+h\right)}^2}\] In this problem, we know that $a_g h=\frac{1}{2}a_g(R)$ so
\begin{gather*} G\frac{M}{(R+h)^2}=\frac{1}{2}G\frac{M}{R^2}\\\\ \Rightarrow (R+h)^2=2R^2\end{gather*}
Taking the square root of both sides, we obtain \[R+h=\pm \sqrt{2}R \] The plus sign sign, gives \[R+h=+\sqrt{2}R \Rightarrow h=(\sqrt{2}-1)R\] and the minus sign get \[R+h=-\sqrt{2} \Rightarrow h=-(1+\sqrt{2})R\] Choosing the minus sign doesn't give the correct answer since $h$ is obtained negative. Therefore, the orbital altitude of the Astronauts is $h=0.41\,R$

(a) The gravitational potential energy of two point particles of masses $m$ and $M$ that are separated by a distance of $r$ is given by the following equation \[U=-G\frac{m_1m_2}{r^2}\] 
First, calculate the gravitational potential energy of an infinitesimal element of the ring $dM$ and mass $m$ then integrate it around the ring to find the total potential.
\begin{gather*} dU=-\frac{Gm}{r}dM\\\\ U=-\frac{Gm}{r}\int{dM}=-\frac{GmM}{\sqrt{x^2+a^2}}\end{gather*}
(b) If $x\gg a$, then using the binomial theorem ${\left(1+u\right)}^n=1+nu+\dots \ $ ($\left|u\right|$ must be smaller than $1$), we obtain 
\begin{align*} U&=-\frac{GmM}{\sqrt{x^2+a^2}}\\\\&=-\frac{GmM}{x{\left(1+\frac{a^2}{x^2}\right)}^{\frac{1}{2}}}\\\\&=-\frac{GmM}{x}{\left(1+\frac{a^2}{x^2}\right)}^{\frac{1}{2}}\\\\&=-\frac{GmM}{x}\left(1-\frac{a^2}{2x^2}\right)\end{align*}
(c) To find the force, we differentiate the potential energy \begin{align*} F_x&=-\frac{dU}{dx}\\\\&=GmM\left(-\frac{1}{2}\frac{2x}{{\left(x^2+a^2\right)}^{\frac{3}{2}}}\right)\\\\&=GmM\frac{x}{{\left(x^2+a^2\right)}^{\frac{3}{2}}}\end{align*}
If we assume $x\gg a$ then \begin{align*} GmM\frac{x}{{\left(x^2+a^2\right)}^{\frac{3}{2}}}&=\frac{GmM}{x^2}{\left(1+\frac{a^2}{x^2}\right)}^{-\frac{3}{2}}\\\\&=\frac{GmM}{x^2}\left(1-\frac{3}{2}\frac{a^2}{x^2}+\dots \right)\\\\ &\cong \frac{GmM}{x^2}\end{align*}
(d) \[U\left(x=0\right)=-GmM/a\] 
\[F_x\left(x=0\right)=GmM\left[\frac{x}{{\left(x^2+a^2\right)}^{\frac{3}{2}}}\right]=0\] 
The contribution from $dM$ around the ring cancels the net force on the particle.