- Home
- Physics Problems
- Problems
Solved Problems
A $40\,{\rm g}$ block of ice is cooled to $-78{}^\circ {\rm C}$ and is then added to $560\, {\rm g}$ of water in an $80{\rm g}$ copper calorimeter at a temperature of $25{\rm {}^\circ C}$. Determine the final temperature of the system consisting of the ice, water, and calorimeter.(${{\rm c}}_{ice}=0.5\,\frac{{\rm cal}}{{\rm g.}{\rm{}^\circ\!C}}{\rm \ ,\ }{{\rm c}}_{{\rm water}}=1\frac{{\rm cal}}{{\rm g.K}}\ ,\ c_{Cu}=0.0923\,\frac{{\rm cal}}{{\rm g.K}}$)
The process of melting ice is as follows \begin{gather*} \underbrace{ice}_{\rm -78^\circ C}\xrightarrow{Q_1}\underbrace{ice}_{\rm 0^\circ C}\xrightarrow{Q_2}\underbrace{water}_{\rm 0^\circ C}\xrightarrow{Q_3}\underbrace{water}_{\rm T_f ^\circ C} \end{gather*}
We can calculate the amount of heat absorbed by the ice as
\begin{align*} Q_1&=m_ic_i\Delta T \\\\ &=(40\ {\rm g})\left(0.5\frac{{\rm cal}}{{\rm g.K}}\right)(0-(-78)) \\\\&=1560\, {\rm cal}\end{align*}
\[Q_2=m_iL_f=(40\, {\rm g})\left(80\,\frac{{\rm cal}}{{\rm g}}\right){\rm =3200\, cal}\]
\[Q_3=m_ic_w (T_f-0)=(40)(1)T_f\]
Now calculate the amount of heat released by the calorimeter and the water
\[\underbrace{water+Calo}_{\rm 25^\circ C}\xrightarrow{Q_4}\underbrace{water+Calo}_{\rm T_f ^\circ C} \]
\begin{align*} Q_4&=\left(m_{cal}\,c_{Cu}+m_wc_w\right)\Delta T\\\\&=\left(\underbrace{80\times 0.0923+560\times 1}_{567.384}\right)\left(T_f-25\right)\end{align*}
Since ${\rm -78^\circ C}<T_f<{\rm 25^\circ C}$, so $Q_4<0$.
Set the negative of the heat released equal to the heats absorbed by the ice (by the first law of thermodynamics), to find the final temperature of the system \begin{gather*} \underbrace{Q_1+Q_2+Q_3}_{Q_{gain}}=-\underbrace{Q_4}_{lost}\\\\ 1560+3200+40\,T_f=-(567.384\,T_f-14184.6) \\\\ \Rightarrow T_f=\rm 15.51^\circ C\end{gather*}
How much heat is needed to melt 20 ${\rm kg}$ of a solid material initially at $-10^\circ {\rm C}$? Given: $c_{material}=2500\ {\rm J/(kg\ C^\circ )}$ , $L_{material}=40\times {10}^4\ {\rm J/kg}$
Recall from the specific heat problems that the heat delivered or absorbed during a change in the temperature of an object is $Q=mc\Delta T$. If we have a phase change in the material, then the amount of heat absorbed or delivered is $Q=\pm mL$, where the plus sign is for the melting process and the minus is for condensation. $L$ is called the latent heat and $c$ is the specific heat capacity of that substance.
In the following, The heat and temperature changes of this solid material are as follows
\begin{gather*} \underbrace{\rm -10^\circ C}_{solid} \xrightarrow{Q_1} \underbrace{\rm 0^\circ C}_{Solid}\xrightarrow{Q_2} \underbrace{\rm 0^\circ C}_{fluid} \\\\ Q_1=mc\Delta T=20\times 2500\times (0-(-10))=50\times {10}^4\ {\rm J}\\\\ Q_2=+mL=20\times 40\times {10}^4=800\times {10}^4\quad {\rm J} \end{gather*} Thus, the total heat is the sum of them as \[Q_{total}=Q_1+Q_2=850\times {10}^4 \quad {\rm J}\]
A person pours $330\, {\rm g}$ of water at $50{\rm{}^\circ\,\!C}$ into an $855\, {\rm g}$ aluminum container with an initial temperature of $10{\rm{}^\circ\,\!C}$. The specific heat of aluminum is $900\, {\rm J/(kg.K)}$ and that of the water is $4190\, {\rm J/(kg.K)}$. What is the final temperature of the system, assuming no heat is exchanged with the surroundings?
The heat released by the water is \begin{align*} Q_1&=m_wc_w(T_f-50) \\ &=(0.330)(4190)(T_f-50)\end{align*} And the heat absorbed by the aluminum is \begin{align*} Q_2&=m_{Al}c_{Al}(T_f-10)\\ &=(0.855)(900)(T_f-10)\end{align*} Duo to the conservation of energy the sum of the two heats must be zero, i.e., $\Sigma Q_{tot}=0$ or the negative of heat lost must be equal to the heat gained $-Q_{lost}=Q_{gained}$, therefore \begin{gather*} -(330)(4190)(T_f-50)=(0.855)(900)(T_f-10) \\ \Rightarrow T_f=\rm 35.67^\circ C \end{gather*}
$2\, {\rm kg}$ of ice at $0{\rm{}^\circ\,\!C}$ is dropped into an insulated container with $5\, {\rm kg}$ of water at $80{\rm{}^\circ\,\!C}$.
(a) Find the final temperature.
(b) Find the entropy change of ice.
(c) Find the total change of entropy.
(a) The process of heat lost by the water is \[ \underbrace{water}_{\rm 80^\circ C} \xrightarrow{Q_1} \underbrace{water}_{\rm T_f^\circ C} \]
Since there is no phase transition, we have \[Q_1=m_wc_w\Delta T=5(4186)(T_f-80) \] And the process of melting ice is as follows \[ \underbrace{ice}_{\rm 0^\circ C}\xrightarrow{Q_2}\underbrace{water}_{\rm 0^\circ C}\xrightarrow{Q_3}\underbrace{water}_{\rm T_f^\circ C}\] As one can see, there is a phase change in this process, so as we learned from latent heat of fusion problems, we must use the formula $Q=mL_f$, which yields \begin{align*} Q_2&=m_iL_f\\ &=2(3.33\times {10}^5) \\ &=666\, {\rm kJ} \\\\ Q_3&=m_ic_w(T_f-0)\\ &=2(4186)(T_f-0) \end{align*} The conservation of energy states that, the amount of released and absorbed heat must be equal or the sum of them must be zero, i.e., $Q_{lost}+Q_{gained}=0$ \begin{gather*} Q_1+Q_2+Q_3=0 \\\\ 4186[5(T_f-80)+2(T_f-0)]+666\times {10}^3=0 \\\\ 4186(7T_f-400)+666\times {10}^3=0 \\\\ \Rightarrow \quad \boxed{T_f=\, \rm 34.41^\circ C}\end{gather*}
(b) By definition, the change in entropy of a system is \[\Delta S=\int^f_i{\frac{dQ_{rev}}{T}}\], where $dQ_{rev}$ is the heat absorbed by the system in a reversible process. Therefore, \begin{align*} \Delta S_i &= \int^{fin}_{ini}{\frac{dQ}{T}} \\ \\ &= \int^{water\ 0^\circ C}_{ice\ 0^\circ C}{\frac{dQ}{T}}+\int^{water\ 34.41^\circ C}_{water\ 0^\circ C}{\frac{dQ}{T}} \\ \\ &= \frac{m_iL_f}{273+0^\circ C}+\int^{273+\ 34.41^\circ C}_{273+\ 0^\circ C}{c_wm_i\frac{dT}{T}}\\ \\ &= \frac{m_iL_f}{273}+m_ic_w \ln \left(\frac{273+34.41}{273}\right) \\\\ &= \frac{2\times 333\times {10}^3}{273}+2(4186) \ln \left(\frac{307.41}{273}\right) \\ \\ &=3433.40\,\rm J/K \end{align*} Note: temperatures must be in Kelvins.
(c) First calculate the change in entropy of water and then find the total change of it
\begin{align*} \Delta S_w&=\int^{water\ 34.41^\circ C}_{water\ 80^\circ C}{\frac{dQ}{T}} \\ \\ &=\int^{273+34.41^\circ C}_{273+80^\circ C}{m_wc_w\frac{dT}{T}} \\ \\ &=m_wc_w \ln \left(\frac{307.41}{353}\right) \\\\ &=5(4186) \ln \left(\frac{307.41}{353}\right) \\\\ &=-2894.31\, {\rm J} \end{align*} The minus sign indicates that the entropy of the water has decreased. \begin{align*} \Delta S_{tot}&=\Delta S_i+\Delta S_w \\&=3433.40-2894.31 \\ &=+538.68\,\rm J/K\end{align*} The entropy change of the universe (total system) is positive, as the second law of thermodynamics requires.
At $10^\circ C$, $32\, {\rm g}$ of water is mixed with $430\, {\rm g}$ of ice at $-5^\circ C$.
\begin{gather*} c_w=4190\, \left(\rm \frac{J}{kg\cdot K}\right) \ , \ c_i=2900\, \left(\rm \frac{J}{kg\cdot K}\right) \\\\ L_f=3.34\times 10^5 \, \left(\rm \frac{J}{kg}\right) \end{gather*} (a) What mass of water freezes?
(b) What is the change in entropy of the system?
(a) First, find the final temperature of the system. The heat released from water is
\[ \underbrace{water}_{\rm 10^\circ C} \xrightarrow{Q_1} \underbrace{water}_{\rm T_f^\circ C}\] And the amount of heat released is also calculated as follows \begin{align*} Q_{lost}=Q_1&=m_wc_w\Delta T \\ &=0.032\times 4190(T_f-10)\end{align*} And the heat absorbed by the ice is \[\underbrace{ice}_{\rm -5^\circ C} \xrightarrow{Q_2} \underbrace{ice}_{\rm 0^\circ C} \xrightarrow{Q_3} \underbrace{water}_{\rm 0^\circ C} \xrightarrow{Q_4} \underbrace{water}_{\rm T_f^\circ C} \] Where the heats are found as below \begin{align*} Q_2&=m_ic_i\Delta T\\&=0.430\times 2090(0-(-5))\\&=4493.5, {\rm J} \\\\ Q_3&=m_iL_f\\&=0.430\times 334000 \\&=143620\, {\rm J} \\\\ Q_4&=m_wc_w\Delta T \\ &=0.430\times 4190(T_f-0)\end{align*} Conservation of energy states that $-Q_{lost}=Q_{absorbed}$ \begin{gather*} -134.08(T_f-10)=4493.5+143620+1801.7\left(T_f-0\right) \\\\ \Rightarrow \quad \boxed{T_f<0} \end{gather*} Since the final temperature is negative, so all of the ice does not melt, and instead some of the water freezes (we have a mixture of ice and water), thus $\boxed{T_f=\rm 0^\circ C}$.
To find the amount of water that freezes, equate the heat absorbed by the ice with the heat released by the $m_X\,{\rm kg}$ of water to reaches ice at $0^\circ{\rm C}$ as follows \[ \underbrace{m_X \, water}_{\rm 10^\circ C} \xrightarrow{Q_1} \underbrace{m_X water}_{\rm 0^\circ C} \xrightarrow{Q'_1} \underbrace{m_X\, ice}_{\rm 0^\circ C}\] And the process for the ice is \[\underbrace{ice}_{\rm -10^\circ C} \xrightarrow{Q_2}\underbrace{ice}_{\rm 0^\circ C}\] According to these processes, the heat absorbed by the ice and released by the water are computed as below \begin{align*} Q_{absorbed}&=Q_2=4493.5\, {\rm J} \\\\ Q_{released}&=m_Xc_w\Delta T+m_XL_f \\&=m_X(4190)(0-10)+m_X(-334000) \\ &=-375900m_X \end{align*} Therefore, applying the principle of the conservation of energy gives us \begin{gather*} Q_{absorbed}=-Q_{released} \\\\ 4493.5=375900m_X \\\\ \Rightarrow \quad \boxed{m_X=0.0119\,\rm kg} \end{gather*} Thus, $11.9\ {\rm g}$ of the $32\ {\rm g}$ of water freezes.
Note: the latent heat of freezing is $m\left(-L_f\right)$ since freezing is the opposite process of fusion.
(b) First, find the change in entropy of water and that of ice then combine them. \begin{align*} \Delta S_i &= \int^{fi}_{ini}{\frac{dQ}{T}} \\\\ &=\int^{\rm 0^\circ C+273}_{\rm -10^\circ C+273}{\frac{dQ}{T}}+\int^{water\ \rm 0^\circ C}_{ice\ \rm 0^\circ C}{\frac{dQ}{T}} \\\\ &= m_ic_i \int^{\rm 0^\circ C+273}_{\rm -10^\circ C+273}{\frac{dT}{T}}+\frac{m_iL_f}{273} \\\\ &=m_ic_i \ln T+\frac{m_iL_f}{273} \\\\ &= (0.430)(2090) \ln \left(\frac{273}{263}\right)+\frac{(0.430)(334000)}{273} \\\\ &= \ \boxed{5568.17\, \rm J/K} \end{align*} And the entropy change of ice water is \begin{align*} \Delta S_w &= \int^{water\ \rm 0^\circ C}_{watre\ \rm 10^\circ C}{\frac{dQ}{T}} \\\\ &=\int^{273+\rm 0^\circ C}_{273+\rm 10^\circ C}{\frac{m_wc_wdT}{T}} \\\\ &=m_wc_w \ln \left(\frac{273}{283}\right) \\\\ &=0.032\times 4190\times \ln \left(\frac{273}{283}\right) \\\\ &= \boxed{-4.82\, \rm J/K} \end{align*} Therefore, the total change in entropy of the system is found to be \[ \Delta S_{tot}=\Delta S_w+\Delta S_i= +5563.35\, {\rm J/K}\] Since $\Delta S_{tot}>0$, so the second law of thermodynamics is satisfied.
A chunk of ice with a mass of $20\ {\rm kg}$ falls into the ocean and melts. Initially, and throughout the melting process, it is at a temperature of $\rm 0^\circ C$. The temperature of the very large body of ocean water around it is fixed at $\rm 5^\circ C$.
(a) Calculate the change in the entropy of the ice, as it is converted to the liquid water, still at $\rm 0^\circ C$.
(b) Calculate the change in the entropy of the ocean water as it supplies the heat to melt the ice.
(c) Calculate the total change in entropy, including its sign.
(a) In the section on the latent heat of fusion practice problems we learned the heat that a substance absorbs during a constant temperature process and a change in its phase occurs is calculated by the formula $Q=\pm mL$. In the melting process, we have $Q=+mL_f$. So
\[Q_{ice}=mL_f=20\times (334\times {10}^3)=6.68\times {10}^6\, {\rm J}\]
Now use the entropy definition and find the change in the entropy of the ice
\begin{align*} \Delta S_{ice}&=\frac{\Delta Q_{ice}}{T}\\\\ &=\frac{6.68\times {10}^6}{\rm 0^\circ C+273.15} \\\\ &=24.455\,\rm J/K \end{align*} Note: in the entropy definition, temperatures must be in Kelvins.
(b) Ice requires $Q_{ice}$ to totally melts and this energy has gained from the ocean water. So, by convention, the ocean water has lost $Q_{ocean}=-Q_{ice}$. Using the definition of the entropy change of the ocean water, we obtain
\begin{align*} \Delta S_{ocean}&=\frac{\Delta Q_{ocean}}{T}\\\\ &=\frac{-6.68\times {10}^6}{\rm 5^\circ C+273.15} \\\\ &=-24.016\,\rm J/K \end{align*}
(c) The total change in the entropy of the system of ice + ocean water is the sum of them
\begin{align*} \Delta S_{tot}&=\Delta S_{ice}+\Delta S_{ocean} \\\\ &=24.455+(-24.016) \\\\ &=+439\,\rm J/K \end{align*} As required by the second law of thermodynamics.
What is the entropy change of
(a) A $12\ {\rm g}$ ice cube that melts completely in a bucket of water whose temperature is just above the freezing point of water?
(b) A $5.0\ {\rm g}$ spoonful of water that evaporates completely on a hot plate whose temperature is slightly above the boiling point of water.
(a) The temperature of water and ice cube are $0{\rm{}^\circ\,\!C}$ so there is a change in phase and the heat absorbed by the ice is determined by
\[Q=mL_f=0.012\times 333000=3996\ {\rm J}\]
Now compute the entropy change of the system by the following relation
\[\Delta S=\frac{\Delta Q}{T}=\frac{3996}{0{\rm{}^\circ\,\!C}+273}=14.6\frac{{\rm J}}{{\rm K}}\]
(b) Similarly, $Q=mL_V=0.005\times \left(2256\times {10}^3\right)=11.28\ {\rm kJ}$
\[\Delta S=\frac{\Delta Q}{T}=\frac{11280}{100{\rm{}^\circ\,\!C}+273}=30.2\frac{{\rm J}}{{\rm K}}\]
A student has just purchased a coffee. The cup has $0.3\ {\rm kg}$ of coffee at $70{\rm{}^\circ\,\!C}$. She adds $0.02\ {\rm kg}$ cream at $5{\rm{}^\circ\,\!C}$. In what follows assume coffee and cream have the same thermal properties as water. ($c_w=4186\frac{{\rm J}}{{\rm kg.}{\rm{}^\circ\,\!C}}\ ,\ L_V=2.26\times {10}^6\frac{{\rm J}}{{\rm kg}}\ ,\ \ L_f=33.5\times {10}^4\frac{{\rm J}}{{\rm kg}}\ ,\ \rho=1\ {\rm g/}{{\rm cm}}^{{\rm 3}}$)
(a) What is the temperature of the coffee after adding cream? assume no heat is lost to the outside world at this point.
(b) For this process, is the entropy change of the universe less than, greater than, or equal to zero?
(c) In 1 minute, the coffee cools by $5{\rm{}^\circ\,\!C}$. In this part only, assume heat loss is entirely due to evaporation. What is the mass of the coffee lost in this 1 minute? You can also ignore the cream.
(a) Let $T_f$ be the final temperature. First find the amount of heat released by the coffee
\[coffee\ 70{\rm{}^\circ\,\!C}\xrightarrow{Q_1}coffee\ T_f\]
\[Q_1=m_{co}c\Delta T=0.3\times 4186\left(70-T_f\right)=1255.8\left(T_f-70\right)\]
Now compute the heat that the cream absorbed
\[cream\ 5{\rm{}^\circ\,\!C}\xrightarrow{Q_1}cream\ T_f\]
\[Q_2=m_{cr}c\Delta T=0.02\times 4186\left(T_f-5\right)=83.72(T_f-5)\]
Equal these two heats, due to the first law of thermodynamics, to find the final temperature i.e. $Q_{abs}=-Q_{releas}$
\[\Rightarrow 83.72\left(T_f-5\right)=-1255.8\left(T_f-70\right)\]
\[\Rightarrow T_f=65.9{\rm{}^\circ\,\!C}\]
(b) First, compute the change in entropy of coffee and cream and then calculate the total change in entropy of the universe.
\begin{align*} \Delta S_{cr} &= \int^{T_f}_{T_i}{\frac{{\rm d}{{\rm Q}}_{{\rm in}}}{T}}=\int^{T_f}_{T_i}{\frac{\left(m_{cr}cdT\right)}{T}} \\ &= m_{cr}c{\ln \left(\frac{T_f}{T_i}\right)\ }=0.02\times 4186\times {\ln \left(\frac{65.9{\rm{}^\circ\,\!C}+273}{5{\rm{}^\circ\,\!C}+273}\right)\ }\end{align*}
\[\Rightarrow \Delta S_{cr}=+16.58\,\frac{{\rm J}}{{\rm K}}\]
\begin{align*}\Delta S_{co} &= \int^{T_f}_{T_i}{\frac{dQ_{in}}{T}}=\int^{T_f}_{T_i}{\frac{m_{co}cdT}{T}}\\&= m_{co}c{\ln \left(\frac{T_f}{T_i}\right)\ }=0.3\times 4186\times {\ln \left(\frac{65.9{\rm{}^\circ\,\!C}+273}{70{\rm{}^\circ\,\!C}+273}\right)\ }\end{align*}
\[\Rightarrow \Delta S_{co}=-15.10\ \frac{{\rm J}}{{\rm K}}\]
\[\Delta S_{universe}=\Delta S_{coffee}+\Delta S_{cream}=-15.10+16.58=+1.48\frac{{\rm J}}{{\rm K}}\]
\[{\rm and\ }\Delta {{\rm S}}_{{\rm surrounding}}=0\ \]
So $\Delta S_{universe}>0$ as it should be, since the second law of thermodynamics states that in an irreversible process the entropy change of the universe is always positive or increased. This process is irreversible since there is a spontaneous flow of heat.
(c) Setting the heat released by the coffee equal to $m_x\ {\rm g}$ of coffee absorbs to evaporate.
\[Q=m_{co}c\Delta T=0.3\times 4186\times 5=6280\ {\rm J}\]
\[Q^{'}=m_xL_V\]
\[Q=Q^{'}\Rightarrow 6280=2.26\times {10}^6m_x\Rightarrow m_x=2.77\ {\rm g}\ \]
A $2\ {\rm kg}$ ice at $0\, {\rm ^\circ\, C}$ is dropped into an isolated container with $5\ {\rm kg}$ of water at $80{}^\circ\, {\rm C}$.
(a) Find the final temperature
(b) Find the entropy change of ice.
(c) Find the total change of entropy.
\[(L_f=333\ {\rm kJ/K}, c_w=4186\ {\rm J/(kg.}{\rm{}^\circ\,\!C}{\rm )})\]
Similar to previous problems
(a) $\Sigma Q_i=0\to Q_{water}+Q_{ice}=0$ When there is no phase change, so we have $Q=mc\Delta T$, in the case of a change in phase of matter, $Q=mL_f$ Thus,
\begin{gather*} m_iL_f+m_ic_w(T_{final}-0)+m_wc_w(T_{final}-80)=0 \\\\ \Rightarrow T_{final}=\frac{m_wc_w80-m_iL_f}{\left(m_i+m_w\right)c_w}=34.4^\circ{\rm C}\end{gather*}
(b) The entropy is obtained as below \begin{align*} \Delta S &= \int^{final}_{initial}{\frac{dQ}{T}}\\\\ &=\int^{0{}^\circ\, C\ water}_{ice}{\frac{dQ}{273}}+\int^{273+34.4}_{273}{\frac{dQ}{T}}\\\\&=\frac{m_iL_f}{273}+\int^{273+34.4}_{273}{m_ic_w\frac{dT}{T}}=\frac{m_iL_f}{273}+m_ic_w{\ln \frac{273+34.4}{273}}\\\\&=\frac{2\times 333\times {10}^3}{273}+2\times 4186{\ln \frac{273+34.4}{273}} \end{align*} Therefore, \[\Delta S_{ice}=3433\quad {\rm J/K}\]
Note: in the definition of entropy, $T$ should be in Kelvin.
(c) Now first determine the $\Delta S_{water}$
\begin{align*} \Delta S_{water} &=\int^{273+34.4}_{273+80}{\frac{dQ}{T}}\\\\&=\int^{307.4}_{353}{m_wC_w\frac{dT}{T}}\\\\&= m_wC_w{\ln \left(\frac{307.4}{353}\right)}\\\\&=5\times 4186\,{\ln \left(\frac{307.4}{353}\right)}\\\\&=-2895\quad {\rm \ J/K} \end{align*} Thus, \[\Delta S_{total}=\Delta S_{ice}+\Delta S_{water}=3933-2895=+538\, {\rm J/K}\]
A $100\, {\rm g}$ ice cube is mixed with a $200\,{\rm cm^3}$ of water at $70^\circ {\rm C}$ and allowed to reach thermal equilibrium in a thermally insulated container.
(a) What is the final temperature of the mixer?
(b) What is the change in entropy of the mixing?
(c) How many joules of energy must be added to the mixer to heat it to $100^\circ {\rm C}$ and vaporize it?
(d) Assuming the water vapor at $100^\circ {\rm C}$ is an ideal gas with a density of $18\, {\rm g/mol}$, what volume will it occupy at a pressure of $1\times {10}^5{\rm Pa}$?
(a) Determine the heat lost and gained during these processes. The process of heat lost by the water is as: $water\, 70^\circ {\rm C}\xrightarrow{Q_1}water\, T_f^\circ {\rm C}$
\begin{align*}Q_{lost}&=m_wc_w\Delta T\\\\&=200\times 4.186\times (t_f-70^\circ {\rm C})\end{align*} Heat gained by the ice follows the process: \[ice\, 0^\circ{\rm C}\xrightarrow{Q_2}water\ 0^\circ {\rm C}\xrightarrow{Q_3}water\, T_f^\circ {\rm C}\] So
\begin{align*} Q_{gain}&=\underbrace{m_iL_f}_{Q_2}+\underbrace{m_ic_w\Delta T}_{Q_3}\\\\&=100\times 80+100\times c_w\times (T_f-0)\end{align*}Now using the conservation of energy that is $Q_{gained}=-Q_{lost}$, we obtain \begin{gather*} -200\times 4.186\times (t_f-70^\circ {\rm C})=8000+100\times 4.186\times T_f \\\\ \Rightarrow T_f=40.3^\circ {\rm C} \end{gather*}
(b) The total change in the entropy of the mixing is the sum of the change in the entropy of each of them so $\Delta S_{mixing}=\Delta S_{water}+\Delta S_{ice}$.
\begin{align*} \Delta S_{mixing} &= \int^{T_f}_{T_i}{\frac{\Delta Q_{water}}{T}}+\int^{T_f}_{T_i}{\frac{\Delta Q_{ice}}{T}}\\\\&=\int^{40.3^\circ {\rm C}+273}_{70^\circ {\rm C}+273}{\frac{m_wc_wdT}{T}}+\underbrace{\frac{m_iL_f}{T(0^\circ {\rm C}+273)}+\int^{40.3^\circ {\rm C}+273}_{0^\circ {\rm C}+273}{\frac{m_ic_wdT}{T}}}_{\Delta S_{ice}} \\\\ &=m_wc_w{\left.{\ln T}\right|}^{313.3}_{343}+\frac{m_iL_f}{273}+m_ic_w{\left.{\ln T\ }\right|}^{313.3}_{273}\\\\& =+11.03\quad {\rm J/K}\end{align*}
(c) We want calculate the amount of energy needed to vaporize the $300\, {\rm g}$ of water, so the process is as \[water\, 40.3^\circ {\rm C}\xrightarrow{Q_1} water\, 100^\circ {\rm C}\xrightarrow{Q_2} vapor\, 100^\circ{\rm C}\] Thus,
\begin{align*} Q_{tot}&=\underbrace{m_wc_w\Delta T}_{Q_1}+\underbrace{m_wL_V}_{Q_2}\\\\&=300\times 4.186+\left(100-40.3\right)+300\times 540\\\\& =234\quad {\rm kJ}\end{align*}
(d) Use the ideal gas law, $PV=nRT$, and find the desired quantity.
\begin{align*} V&=\frac{nRT}{P}\\\\&=\left(\frac{300}{18}\right)\frac{8.314\times (100^\circ{\rm C}+273)}{{10}^5}\\\\&=0.517\quad {\rm m^3} \end{align*}
An ice-cube with mass $0.010\ {\rm kg}$ is removed from the freezer and placed into a glass of water. The temperature of the ice-cube before being put into the glass is $-8.5{\rm {}^\circ\, C}$, and the mass of the glass itself (with no water) is $0.100\ {\rm kg}$. The initial temperature of the water in the glass in $20.0{\rm {}^\circ\, C}$, and the final temperature of the water (after the ice cube has all melted and turned to water) is $16.9{\rm {}^\circ\, C}$.
(a) Calculate the entire heat gained by the ice-cube.
(b) By assuming that all of the heat gained by the ice-cube - what you have just calculated in part (a) - equals the heat lost by the glass and the water originally in the glass, calculate the mass of the water which was in the glass.
\[(c_{ice}=2100\frac{{\rm J}}{{\rm kg.}{\rm{}^\circ\,\!C}}\ ,\ \ c_{glass}=840\ \frac{{\rm J}}{{\rm kg.}{\rm{}^\circ\,\!C}}\ ,\ \ L_f=3.33\times {10}^5\frac{{\rm J}}{{\rm kg}}\ \ ,\ \ c_w=4186\ \frac{{\rm J}}{{\rm kg.}{\rm{}^\circ\,\!C}})\]
(a)
\[{\rm ice-8.5}{\rm{}^\circ\,\!C}\xrightarrow{Q_1}{\rm ice\ 0}{\rm{}^\circ\,\!C}\xrightarrow{Q_2}{\rm water\ 0}{\rm{}^\circ\,\!C}\xrightarrow{Q_3}{\rm water\ 16.9}{\rm{}^\circ\,\!C}\]
Heat lost or gained without change in phase is given by $Q=mc\Delta T$ and during phase change is given by $Q=mL$ where $L$ is the latent heat of the substance and $c$ is the specific heat of it. Therefore
\[Q_1=m_{ice}c_{ice}\Delta T_{ice}=\left(0.01\right)\left(2100\right)\left(0-\left(-8.5\right)\right)=178.5\ {\rm J}\]
\[Q_2=m_{ice}L_f=\left(0.01\right)\left(3.335\right)=3330\ {\rm J}\]
\[Q_3=m_{ice}c_w\Delta T=\left(0.01\right)\left(4186\right)\left(16.9\right)=707.4\ {\rm J}\]
The total heat gained by the ice is $Q_{gained}=Q_1+Q_2+Q_3=4216\ {\rm J}$
(b) The total heat lost by the water and glass is
\[({\rm water+glass)\ 20}{\rm{}^\circ\,\!C}\xrightarrow{Q_4}{\rm \ (water+glass)\ }{\rm 16.9}{\rm{}^\circ\,\!C}\]
\[Q_{lost}=Q_4=m_wc_w\Delta T_w+m_gc_g\Delta T_g=\left(m_wc_w+m_gc_g\right)\Delta T\]
Note: the glass and the water experience a similar temperature change i.e. $\Delta T_w=\Delta T_g$
Note: conservation of energy states that the heat gained must be equal to the negative of the heat lost so: $-Q_{lost}=Q_{gained}$
\[\Rightarrow \ \left(m_wc_w+m_gc_g\right)\Delta T=4216\to -\left(m_w\left(4186\right)+0.100\left(840\right)\right)\left(16.9-20\right)=4216\]
\[\therefore m_w=0.305\ {\rm kg}\]
A molten lead of mass ${\rm 0.2\ kg}$ and temperature ${\rm 350{}^\circ\, C}$ is poured into a die-cast made of aluminum. The mass of the cast is ${\rm 0.8\ kg}$ and the initial temperature is ${\rm 25{}^\circ\, C}$.
(a) How much heat is given off as the lead cools from liquid to solid at ${\rm 327{}^\circ\, C}$?~Hint: There are two parts to this calculation; ($i$) the heat given off in going from ${\rm 350{}^\circ\, C}$ to ${\rm 327{}^\circ\, C}$ in the liquid state, and ($ii$) the change in phase at ${\rm 327{}^\circ\, C}$ going from liquid to solid
(b) What is the equilibrium temperature of the system assuming no heat loss?
\[(L_{f-Pb}=2.5\times {10}^4\ {\rm J/kg} \quad, c_{Pb}=450\ {\rm J/(kg.}{\rm{}^\circ\,\!C}{\rm )}\quad, c_{Al}=900\ {\rm J/(kg.}{\rm{}^\circ\,\!C}{\rm )})\]
We can solve this question, from the principles that we learned from the heat practice problems page as below.
(a) The process is as follows \begin{gather*} \underbrace{\rm Pb_{liquid}}_{\rm 350^\circ C} \xrightarrow{Q_1} \underbrace{\rm Pb_{liquid}}_{\rm 327^\circ C} \xrightarrow{Q_2}\underbrace{\rm Pb_{solid}}_{\rm 327^\circ C} \\\\ Q_1=m_{Pb}c_{Pb}\Delta T=0.2\times 450\times (327-350)=-2070\, {\rm J} \\\\ Q_2=m_{Pb}(-L_f)=0.2\times 2.5\times {10}^4=-5000\ {\rm J} \end{gather*} Note: the heat required to change the phase of a given pure substance is $Q=\pm mL$, the minus sign is used when it freezes (heat leaving), and plus sign (heat entering) is used when the material melts. In this case, the lead loses its heat and becomes solid (freeze) so we must use the minus sign.
In the above, the negative indicates that the lead has lost the heat and there is no other significance so the total heat lost going from the liquid lead at $\rm 350^\circ C$ to solid lead at $\rm 327^\circ C$ is \[Q_{total}=\left|Q_1+Q_2\right|=5000+2070=7070\, {\rm J}\]
(b) \begin{gather*} \underbrace{\rm Pb-liquid}_{\rm 350^\circ C} \xrightarrow{Q_1} \underbrace{\rm Pb-liquid}_{\rm 327^\circ C} \xrightarrow{Q_2} \underbrace{\rm Pb-solid}_{\rm 327^\circ C}\xrightarrow{Q_3}\underbrace{\rm Pb-solid}_{\rm T_f} \\\\ Q_3=m_{Pb}c_{Pb}\Delta T=0.2\times 450(T_f-327) \end{gather*} The total heat lost by lead is also found as below \[Q'_{tot}=7070+0.2\times 450(T_f-327)\]
Now calculate the heat that the cast has gained \begin{gather*} \underbrace{cast}_{\rm 25^\circ C}\xrightarrow{Q_{gained}}\underbrace{cast}_{T_f} \\\\ Q_{gained}=m_{Al}c_{Al}\Delta T=0.8\times 900(T_f-25) \end{gather*}
Therefore, according to the conservation of the energy $Q_{gained}=-Q_{lost}$, we have \begin{gather*} 7070+0.2\times 450(T_f-327)=0.8\times 900(T_f-25) \\\\ \Rightarrow T_f=\rm 67^\circ C \end{gather*}
A tank contains $600\ {{\rm m}}^{{\rm 3}}$ of neon at an absolute pressure of $1.01\times {10}^5{\rm \ Pa}$. The temperature of the gas is increased from $300\ {\rm K}$ to $302\ {\rm K}$. What is the increase in the internal energy of the neon?
The given information are $P_i=1.01\times {10}^5{\rm Pa\ ,\ }{{\rm V}}_{{\rm i}}{\rm =600}{{\rm m}}^{{\rm 3}}\ ,\ T_i=300{\rm k}$.
The internal energy of an ideal gas is given by $E_{int}=C_V\Delta T$, where $C_V$ is the heat capacity at constant volume. For an monoatomic gasses ($He, Ne, Ar, Kr, Xe,\dots$) $C_V=\frac{3}{2}nR$ and for all diatomic gasses ($N_2, H_2, O_2,CO,\dots $) $C_V=\frac{5}{2}nR$. Therefore, the change in the internal energy of neon gas (monatomic) is \textit{}
\[\Delta E_{int}=\frac{3}{2}nR\Delta T\]
Since the combination $nR$ is not given, we have used the ideal gas law and replaced it by the following
\[P_iV_i=nR\,T_i\ \Longrightarrow nR=\frac{P_iV_i}{T_i}\]
\[\Delta E_{int}=\frac{3}{2}\left(\frac{P_iV_i}{T_i}\right)\Delta T=\frac{3}{2}\frac{\left(1.01\times {10}^5\right)\left(600\right)}{300}\left(302-300\right)\]
\[\Delta E_{int}=6.06\times {10}^5{\rm J}\]
Important note: the internal energy of an ideal gas depends only on its absolute temperature, not on its pressure or volume.
The temperature of 5 moles of an ideal gas is 200 ${\rm K}$. how much work does the gas do in expanding isothermally to two times its initial volume? Given: ideal gas constant $R=8.31\ {\rm J/(mol\ K)\ }$,
\[{\ln 2\ }=0.7\ ,{\ln \frac{1}{2}\ }=-0.7\ ,{\ln 3\ }=1.1\ ,{\ln \frac{1}{3}\ }=-1.1\ ,{\ln 5\ }=1.6\ ,{\ln \frac{1}{5}\ }=-1.6\]
By definition, the work done on the gas is $W_{on}=-P\Delta V$ and we know that $W_{on}=-W_{by}$ so the work done by the gas in an isothermal expanding is as follows
\[W_{by}=\int{PdV}=\int^{V_f}_{V_i}{nRT\frac{dV}{V}}\]
\[W_{by}=nRT\,{\ln \frac{V_f}{V_i}\ }=5\left(8.31\right)\left(200\right){\ln \frac{2V_i}{V_i}\ }\]
\[W_{by}=8.31\times 1000\times 0.7=5817\ {\rm J\ \ }\Longrightarrow {\rm W\sim \ 6000\ J}\]
In above we have used the ideal gas law $P=nRT/V$.
A gas is initially at (${\rm 20\ Pa,\ 8\ }{{\rm m}}^{{\rm 3}}$) and expands to (${\rm 27\ Pa,\ 12\ }{{\rm m}}^{{\rm 3}}$) .The minimum amount of pressure the gas can be under is ${\rm 9\ Pa}$, and the maximum pressure the gas can be under is ${\rm 40\ Pa}$. Find the minimum amount of work that can be done by the gas in going from its initial state to its final state.
The work done on a gas is defined as the negative of the product of pressure and the 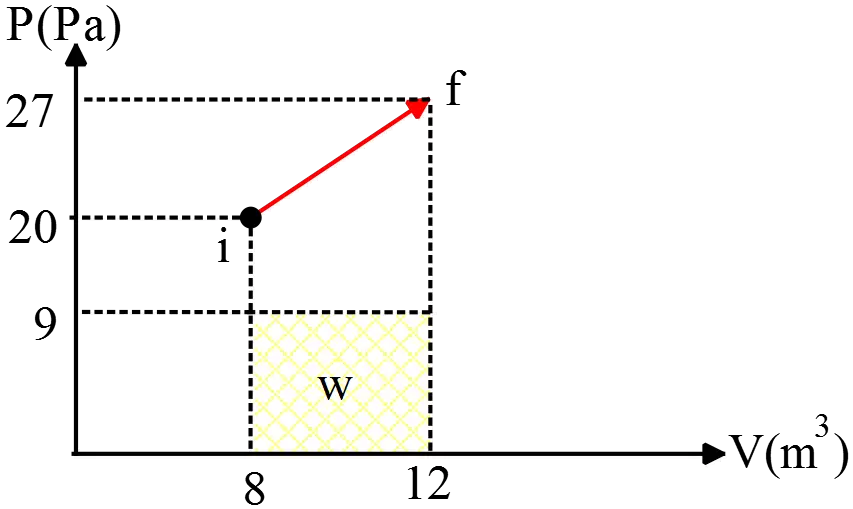 change in the volume of the gas i.e.
change in the volume of the gas i.e.
\[W_{on}=-\int^{V_f}_{V_i}{PdV}\]
By convention, the work done by the gas is negative of the work done on the gas so
\[W_{by}=-W_{on}\]
When a $PV$ diagram has been given, the work done by the gas is the area under the diagram. In this case, the minimum of work is
\[W_{min}=P_{min}\left(V_f-V_i\right)=9\left(12-8\right)=36\ {\rm J}\]
One-mole of an ideal monoatomic gas has the $PV$ diagram as shown in the figure: 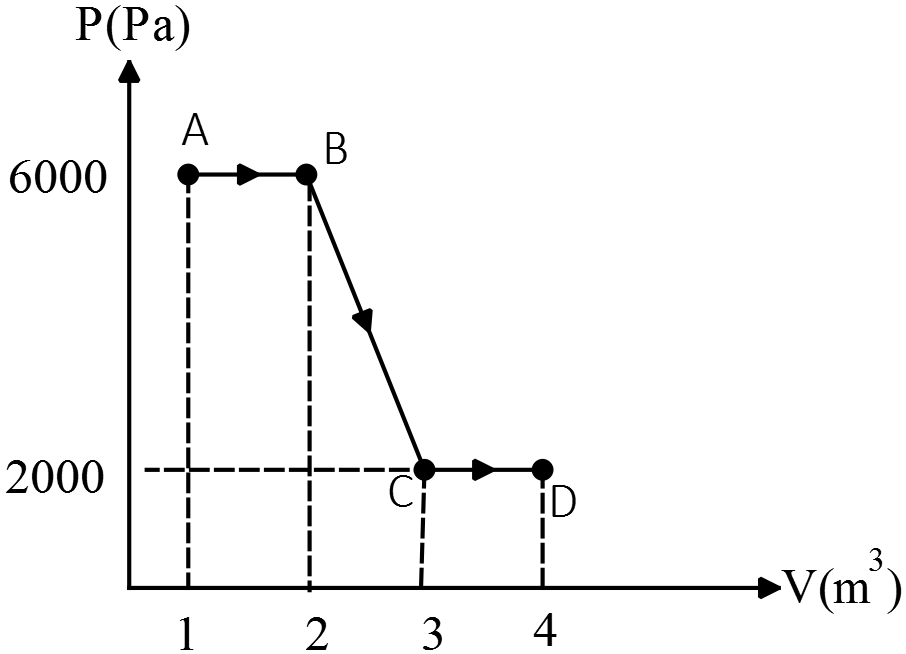
(a) Find the temperature at $A$ and $B$
(b) Find the works $W_{AB},W_{BC},W_{CD}$ done on the gas.
(c) Find the total heat exchanged from $A$ to $D$.
(a) Use the equation of state for an ideal gas, $PV=nRT$
\[T_A=\frac{P_AV_A}{nR}=\frac{6000\times 1}{1\times 8.314}=721.6\ {\rm K}\]
\[T_D=\frac{P_DV_D}{nR}=\frac{6000\times 4}{1\times 8.314}=962.2\ {\rm K}\]
(b) The work done on the system is given by $W_{on}=-P\Delta V$ or its magnitude by the area under the $P-V$ diagram. So
\[W_{AB}=-P\left(V_B-V_A\right)=-6000\left(2-1\right)=-6000\ {\rm J}\]
\[\left|W_{BC}\right|=S_{trapezoid}=\frac{\left(2000+6000\right)\left(3-2\right)}{2}=4000\ {\rm J}\]
Since $\Delta V_{BC}>0\ $so due to $W=-P\Delta V$, the work done on the gas is negative i.e. $W_{BC}=-4000\ {\rm J}$
\[W_{CD}=-P\Delta V_{CD}=-2000\left(4-3\right)=-2000\ {\rm J}\]
(c) Use the first law of thermodynamics i.e. $\Delta U_{int}=W_{on}+Q_{in}$ and that the change in internal energy of an monoatomic ideal gas is ${\Delta U}_{int}=\frac{3}{2}nR\Delta T$, to find the desired heat
\[\frac{3}{2}nR\left({{\rm T}}_{{\rm D}}{\rm -}{{\rm T}}_{{\rm A}}\right){\rm =}{\left({{\rm W}}_{{\rm AD}}\right)}_{on}+Q_{in}\]
\[W_{AD}=W_{AB}+W_{BC}+W_{CD}=-6000-4000-2000=-12000\ {\rm J}\]
\[\Rightarrow \ Q_{in}=\frac{3}{2}nR\left(T_D-T_A\right)-\left(-12000\right)=\frac{3}{2}\left(P_DV_D-P_AV_A\right)+12000\]
\[\Rightarrow Q_{in}=\frac{3}{2}\left(2000\times 4-6000\times 1\right)+12000=+15000\ {\rm J}\]
Where in the third line we have replaced the $nRT$ by $PV$ to avoid uncertainty in the result. Since $Q_{in}>0$ thus the total heat absorbed by the gas.
Problem (17): A heat engine operates using the cycle shown in the figure. The working substance is  2 mol helium gas, which reaches a maximum temperature of $327^{\circ}$. Assume that the helium can be treated as an ideal gas. Process bc is isothermal. The pressure in states a and b is ${10}^5\,{\rm Pa}$ and the pressure in state b is $3\times {10}^5\,{\rm Pa}$.
2 mol helium gas, which reaches a maximum temperature of $327^{\circ}$. Assume that the helium can be treated as an ideal gas. Process bc is isothermal. The pressure in states a and b is ${10}^5\,{\rm Pa}$ and the pressure in state b is $3\times {10}^5\,{\rm Pa}$.
(a) How much heat enters the gas and how much leaves the gas each cycle?
(b) How much work does the engine do each cycle, and what is its efficiency?
(c) Compare this engine efficiency with the maximum possible efficiency attainable with the hot and cold reservoirs used by this thermodynamic cycle.
Solution:
(a) First, find the temperatures of $a,b,c$ states. Because of $PV\sim T$ and maximum attainable temperature is $327^{\circ}$ and $bc$ is isothermal $T_b=T_c=327^{\circ}$ so we have \[P_aV_a<P_bV_b\ or\ P_cV_c\to T_a<T_b=T_c\]Applying the ideal gas law get \begin{align*} \frac{P_a}{T_a}&=\frac{P_b}{T_b}\\ \to T_a&=T_b\frac{P_a}{P_b}\\&=\left(273+373\right)\frac{1\times {10}^5}{3\times {10}^5}\\&=200{\rm K}\end{align*}
Now applying the first law of thermodynamics as $\Delta U_{int}=\rm{\Delta W_{on}+ \Delta Q_{in}}$ we can get the desired heat in each process.
In the process $a\to b$, we have
\[\Delta V_{a\to b}=0 \Rightarrow \Delta W_{a\to b}=-P\Delta V=0 \] Thus, the heat in the process $ab$ is \begin{align*} \Delta U_{a \to b}&=\Delta Q_{a\to b}\\&=nC_{V}\Delta T\\ &=2\left(\frac{3}{2}R\right)(T_b - T_a)\\&=3(8.314)(600-200)\\&=9.97\times10^{3}\,{\rm J}\end{align*} The bc process is isothermal so \begin{gather*}\Delta T_{b\to c}=0\\\Rightarrow \Delta U_{b\to c}=0\\\Rightarrow \Delta Q=-\Delta W\end{gather*} Recall that the work done on a gas in an isothermal process is as below \begin{align*} W_{isothermal}&=-\int{PdV}\\&=-\int^{V_f}_{V_i}{\frac{nRT}{V}dV}\\&=-nRT \ln \frac{V_f}{V_i} \end{align*}Therefore, the rquired heat in the $bc$ process is obtained as \begin{align*} \Delta Q_{b\to c}&=nRT{\ln \frac{V_c}{V_b}\ }\\&=2(8.314)(600){\ln \left(\frac{T_c}{T_b}\frac{P_b}{P_c}\right)\ }\\&=9976.8\,{\ln 3\ }\end{align*} And in the process $ac$ which is an isobaric, we have $\Delta P_{c\to a}=0$, therefore the heat gained or lost in this process is \begin{align*} \Delta Q_{c\to a} &= \Delta U_{c\to a}-\Delta W_{c\to a}\\&=\frac{3}{2}nR\left(T_a-T_c\right)+\underbrace{P\left(V_a-V_c\right)}_{nR\left(T_a-T_c\right)}\\&=\frac{5}{2}nR\left(T_a-T_c\right)\\ &=\frac{5}{2}\left(2\right)\left(8.134\right)\left(200-600\right)\\&=-1.66\times {10}^4\ {\rm J} \end{align*}Now the signs of heats determine whether heat absorbed or lost by the system. $\Delta Q_{a\to b}>0$ and $\Delta Q_{b\to c}>0$ so heat enters the gas and $\Delta Q_{c\to a}<0$ so heat leaves the gas.
Note: Change in the internal energy of a monoatomic gas is $\Delta U_{int}=\frac{3}{2}nRT$. Helium is such a gas.
(b) In a cycle $\Delta T=0$ then $\Delta U=\frac{3}{2}nR\Delta T=0$ so $\Delta Q_{cycle}=-\Delta W_{cycle}$. The amount of heat enters the system (gas) is \begin{align*}Q_{in}&=Q_{ab}+Q_{bc}\\&=9.97\times {10}^3+1.1\times {10}^4\\&=2.097\times {10}^4\, {\rm J}\end{align*} and the lost heat is $Q_{out}=Q_{ca}=1.66\times {10}^4\,{\rm J}$Therefore, the change in the heat of the system is as below \begin{align*} \Delta Q_{cycle}&=Q_{net}\\&=Q_{in}-Q_{out}\\&=\left(2.097-1.66\right)\times {10}^4\\&=4.4\times {10}^3\ {\rm J}\end{align*}Thus, the magnitude of the work done on or by the system is obtained as $ \left|\Delta W\right|=4.4\times {10}^3\ {\rm J}$ and consequently, the efficiency of the cycle is
\[e=\frac{W}{Q_{in}}=0.21=21\%\]
(c) Recall that the most efficient heat engine is the Carnot cycle which is obtained as $e_{Carnot}=1-\frac{T_C}{T_H}$
So in a cycle, we have \begin{align*} e_{max}&=e_{Carnot}\\ \\&=1-\frac{T_C}{T_H}\\\\&=1-\frac{200}{600}\\ \\&=\frac{2}{3}\\&=66\%\end{align*}
A cylinder contains 7.1 moles of ideal gas, initially at a temperature of ${\rm 97{}^\circ\, C}$. The cylinder is provided with a frictionless piston, which maintains a constant pressure of $5.5\times {10}^5\ {\rm Pa}$ on the gas. The gas is cooled until its temperature has decreased to $27{\rm{}^\circ\,\!C}$. For the gas $C_V=12.24\ {\rm J/(mol.K)}$. The gas constant $R=8.314\ {\rm J/(mol.K)}$. Calculate:
(a) the work $W$ done by gas
(b) The net change in the internal energy, $\Delta U$, of the gas, and
(c) The heat transfer $Q$.
(a) By definition, the work done on the gas is $W_{on}\ =-P\Delta V$, so
\begin{align*} W&=-P\left(\frac{nRT_2}{P}-\frac{nRT_1}{P}\right)\\ \\&=-nR\left(T_2-T_1\right)\\ \\&=-\left(7.1\right)\left(8.314\right)\left(300-370\right)\\ \\&=+4132.058\quad {\rm J}\end{align*} Since the volumes of the gas is unknown, we have used the ideal gas law $V=nRT/P$ .
(b) The change in internal energy of an ideal gas in general is given by \begin{align*}\Delta U_{int}&=nC_V\Delta T\\ &=7.1\times 12.24\left(300-370\right)\\&=-6083.28\quad{\rm J}\end{align*} Note: for ideal gases, the equation above is always valid, even when the volume isn't constant as this case!
(c) Use the first law of thermodynamics to find $Q$ \begin{align*}\Delta U_{int}&=Q_{trans}+W_{on}\\ \Rightarrow \quad Q_{trans}&=-6083.28-\left(+4132.058\right)\\ &=-10215.338\quad {\rm J}\end{align*} Since $Q_{trans}<0$ so the heat lost by the gas.
In a constant-volume process $1000\ {\rm J}$ of heat is transferred to $1.0\ {\rm mol}$ of a monoatomic ideal gas initially at $300\ {\rm K}$. Find: ($C_V=\frac{3}{2}R$)
(a) The work done on the gas
(b) The change in the internal energy of the gas
(c) The final temperature.
(a) Given data: $Q_{in}=1000\ {\rm J}$ , $T_i=300{\rm \ K}$, $W_{on}=?$
By definition, $W_{on}=-P\Delta V=0\ $since $\Delta V=0$
(b) Use the first law of thermodynamics as $\Delta U_{int}=Q_{in}+W_{on}$
\[\Delta U_{int}=+1000+0=+1000\ {\rm J}\]
(c) The heat transferred in a constant volume by a system is given by $Q=nC_V\Delta T$
\[\Rightarrow \ +1000=\left(1\right)\frac{3}{2}\left(8.314\right)\left(T_f-300\right)\Rightarrow T_f=380.18\ {\rm K}\]
A $2\ {\rm mol}$ sample of an ideal diatomic gas is taken through the cycle shown in the figure. The process BC is an isothermal expansion. Calculate: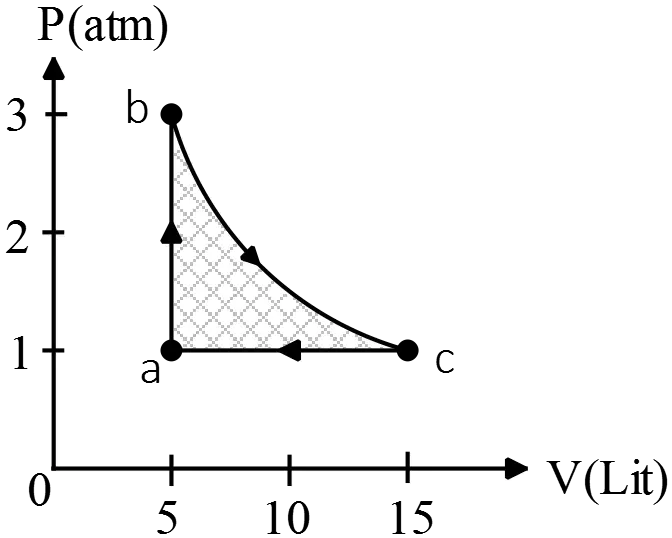
(a) The energy added to the gas by heat
(b) The energy exhausted from the gas by heat
(c) The net work done on the gas
(d) The efficiency of the cycle.
(a) Use the first law of thermodynamics to find the heat exchanged of each process.
BC is isothermal i.e.$\Delta T=0$, thus \begin{gather*} \Delta U_{int}=nC_V\Delta T=0 \\ \\ {\left(\Delta U_{int}\right)}_{BC}={\left(Q_{in}+W_{on}\right)}_{BC}\\ \\ \Rightarrow 0=Q_{in}+W_{on}\end{gather*}
\begin{align*}Q_{BC}=-W_{BC}&=-\left(-\int{PdV}\right)\\ \\&=\int^{V_f}_{V_i}{\frac{nRT}{V}dV}\\ \\&=\underbrace{nRT}_{PV}{\ln \frac{V_f}{V_i}\ }\end{align*}Thus, the heat in the BC part is computed as below \begin{align*} Q_{BC}&=P_BV_B{\ln \frac{V_C}{V_B}\ }\\ \\&=\left(3\times 1.01\times {10}^5{\rm Pa}\right)\left(5\times {10}^{-3}{{\rm m}}^{{\rm 3}}\right){\ln \frac{15}{5}}\\ \\&=+1664.39\ {\rm J}\end{align*} For the $CA$ process, we have \begin{gather*}\Delta P=0 \\ \\ Q_{CA}=nC_P\Delta T_{CA}=\left(\frac{7}{2}R\right)n\left(T_A-T_C\right)\end{gather*} Therefore,\begin{align*} Q_{CA}&=\frac{7}{2}\left(P_AV_A-P_CV_C\right)\\ \\ &=\frac{7}{2}\left(5\times 1-15\times 1\right)\left({\rm atm.L}\right)\\ \\&=-35\left({\rm 1.01\times }{{\rm 10}}^{{\rm 5}}{\rm Pa.}(10^{-3}\,{\rm m^3})\right)\\ \\&=-3535\ {\rm J} \end{align*} For the isochoric process $AB$, we have \begin{gather*} \Delta V=0 \\ \\ Q_{AB}=nC_V\Delta T_{AB}=n\left(\frac{5}{2}R\right)\left(T_B-T_A\right)\end{gather*} Therefore, \begin{align*} Q_{AB}&=\frac{5}{2}\left(P_BV_B-P_AV_A\right)\\ \\&=\frac{5}{2}\left(3-1\right){\rm atm\times 5L=25\quad atm.L} \\ \\ &=25\left(1.01\times {10}^5\right)\left({10}^{-3}\right) \\ \\&=+2525\quad {\rm J}\end{align*}
By convention, if $Q_{in}>0$ then heat transferred into the system (gas).Therefore, the total heat absorbed by the gas is $Q_h=Q_{AB}+Q_{BC}=2525+1664.39=4189.39\ {\rm J}$
Note: in above, instead of calculating temperatures of each point, we have used the ideal gas law to convert $nRT$ into $PV$. (Since the data is given in terms of $P$ and $V$)
Note: for an diatomic gas $C_V=\frac{5}{2}R$ and in general $C_P=C_V+R=\frac{7}{2}R$.
(b) By convention, if $Q_{in}<0$ then the heat released from the gas into the surrounding thus in this case $Q_c=Q_{CA}=-3535\ {\rm J}$
(c) Gas absorbed the $Q_h$ from hot reservoir, does work $W_{net}$ and gives up $Q_c$ to the cold reservoir so due to the 2${}^{nd}$ law of thermodynamics we have \begin{align*} \left|W_{net}\right|&=\left|Q_h\right|-\left|Q_c\right|\\&=4189.39-3535\\&=654.39\quad {\rm J}\end{align*}
(d) The thermal efficiency of a heat engine is defined as the work done by the engine $W_{net}$ divided by the heat absorbed during one cycle i.e. \begin{align*} e&=\frac{W_{net}}{\left|Q_h\right|}\\ \\&=1-\frac{\left|Q_c\right|}{\left|Q_h\right|}\\ \\&=1-\frac{3535}{4189.39}\\ \\&=15.6\,\% \end{align*}
(a) One liter of a gas with $\gamma=1.3\ $is at $273{\rm K}$ and $1.0\ {\rm atm}$ pressure. It is suddenly compressed adiabatically to half its original volume. Find its final pressure and temperature
(b) The gas is now cooled back to $273\ {\rm K}$ at constant pressure. What is its final volume?
Given data: $T_1=273\ {\rm K\ ,\ }{{\rm P}}_{{\rm 1}}=1\ {\rm atm\ ,\ \ }{{\rm V}}_{{\rm 1}}{\rm =1\ lit\ ,\ }{{\rm V}}_{{\rm 2}}{\rm =0.5\ lit\ ,\ \ }{{\rm P}}_{{\rm 2}}{\rm =?,\ \ }{{\rm T}}_{{\rm 2}}{\rm =?\ \ }$
(a) In the adiabatic process the equation of state is $PV^\gamma={\rm constant}$ or $TV^{\gamma-1}={\rm constant}$. So
\[P_1V^\gamma_1=P_2V^\gamma_2\Rightarrow P_2=P_1{\left(\frac{V_1}{V_2}\right)}^\gamma=\left(1\right){\left(\frac{1}{0.5}\right)}^{1.3}=2.46\ {\rm atm}\]
\[T_1V^{\gamma-1}_1=T_2V^{\gamma-1}_2\Rightarrow T_2=T_1{\left(\frac{V_1}{V_2}\right)}^{\gamma-1}=273{\left(\frac{1}{0.5}\right)}^{1.3-1}=336.1\ {\rm K}\]
(b) Use the ideal gas law $PV=nRT$ between these points to find the final volume
\[\frac{P_2V_2}{T_2}=\frac{P_fV_f}{T_f}\Rightarrow V_f=V_2\left(\frac{T_f}{T_2}\right)=\left(0.5\right)\left(\frac{273}{336.1}\right)=0.406\ {\rm lit}\]
One mole of an ideal diatomic gas goes from $a$ to $c$ along the diagonal path in the 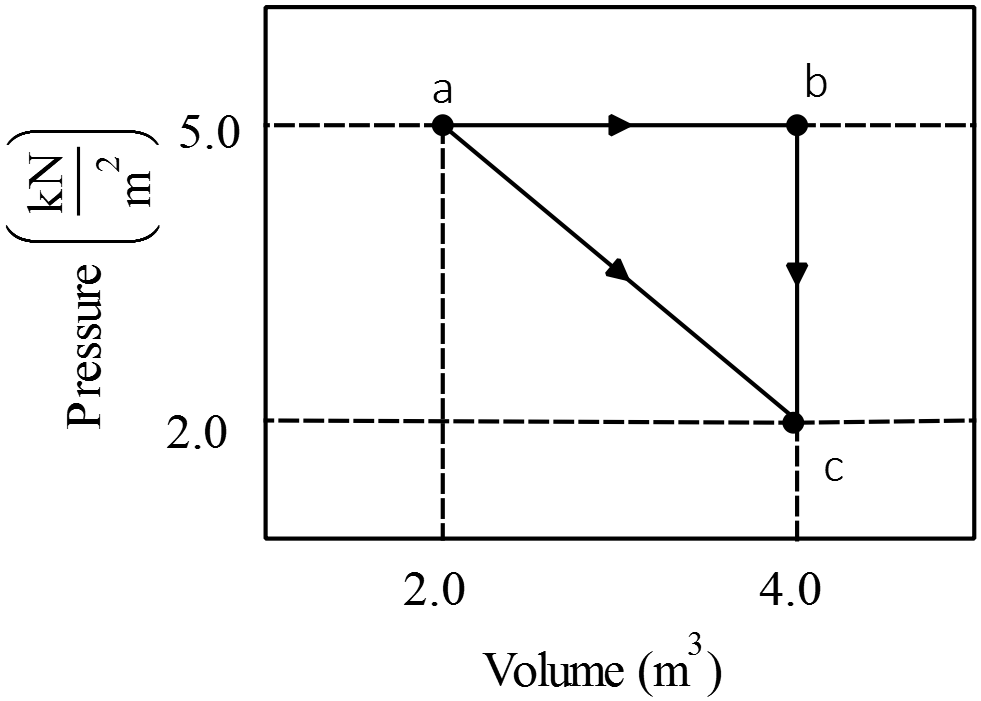 figure below. During the transition,
figure below. During the transition,
(a) What is the change in internal energy of the gas
(b) How much energy is added to the gas as heat?
(c) How much heat is required if the gas goes from $a$ to $c$ along the indirect path $abc$?
(d) What is total heat absorbed by the gas? And what is total work done on the gas?
(a) Use the definition of the internal energy as $U_{int}=nC_V\Delta T$. Recall that for an ideal diatomic gas $C_V=\frac{5}{2}R$ so
\[\Delta U_{int}=\frac{5}{2}nR\left(T_c-T_a\right)\xrightarrow{ideal\ gas\ law}\Delta U_{int}=\frac{5}{2}\left(P_cV_c-P_aV_a\right)\]
\[\Rightarrow \Delta U_{int}\left(a\to c\right)=\frac{5}{2}\left(2000\times 4-5000\times 2\right)=-5000\ {\rm J}\]
Note: the change in internal energy of a system is independent of the path and only dependent on the initial and final temperatures of the system, as the formula shows this fact.
(b) See part (d), $Q\left(a\to c\right)=+2000\ {\rm J}$
(c) See part (d), $Q\left(a\to b\to c\right)=Q_1+Q_2=35000-30000=+5000\ {\rm J}$
(d) To solve this part, calculate work and heat of each process individually.
\[a\to b\ :isobaric\ \left(\Delta P=0\right)\]
\[\ \ W_1=area\ under\ curve=\left(4-2\right)5000=10000\ {\rm J}\]
\begin{align*} Q_1 &=nC_P\Delta T_{ab}=n\ \left(C_V+R\right)\left(T_b-T_a\right)\\ &=\frac{7}{2}\left(P_bV_b-P_aV_a\right)=\frac{7}{2}\left(5000\right)\left(4-2\right)=35000\ {\rm J} \end{align*}
\[b\to c:isochoric\left(\Delta V=0\right),\ \ W_2=-P\Delta V=0\]
\begin{align*} Q_2 &=nC_V\Delta T_{bc}=\frac{3}{2}nR\left(T_c-T_b\right)\\ &=\frac{5}{2}\left(P_cV_c-P_bV_b\right)=\frac{5}{2}\left(2000-5000\right)\left(4\right)=-30000\ {\rm J}\end{align*}
\begin{align*} a\to c\ :W_3=area\ under\ curve(trapezoid)&=\frac{1}{2}(2000+5000)(4-2)\\ &=7000\ {\rm J}\end{align*}
\[Q_3=\Delta U_{int}\left(a\to c\right)-W_3=-5000-\left(-7000\right)=+2000\ {\rm J}\]
Note: since in this case $\Delta V_{ac}>0$ and $\Delta V_{ab}>0\ $so by definition of work done on the gas i.e. $W_{on}=-P\Delta V$, we have $W_3=-7000\ {\rm J}$ and $W_1=-10000\ {\rm J}$
Therefore the total heat added to the system, by convention (i.e. $Q_{in}>0$), is
\begin{gather*} Q_{in}=Q_1=35000{\rm \ J}\\ \\ W_{on}=-10000-7000=-17000\ {\rm J}\end{gather*}
Note: the area under $P-V$ diagram, gives the magnitude of the work done on the gas. To find the correct sign ($\pm $), we must use the formal definition of the work done on the gas that is $W_{on}=-P\Delta V$. If $\Delta V>0$, then $W_{on}<0$ and vice versa.
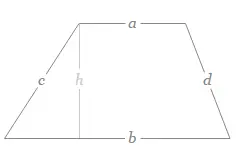
Note: the area of a trapezoid is as follows \[S=\frac{a+b}{2}h\]
When $20.9\ {\rm J}$ was added as heat to a particular ideal gas, the volume of the gas changed from $50.0\ {{\rm cm}}^{{\rm 3}}$ to $100\ {{\rm cm}}^{{\rm 3}}$ while the pressure remained constant at $1.00\ {\rm atm}$.
(a) By how much did the internal energy of the gas change?
If the quantity of gas present is $2.00\times {10}^{-3}{\rm mol}$, find the molar specific heat of the gas at
(b) Constant pressure
(c) Constant volume.
(a) $20.9\ {\rm J}$ heat was added to the gas that is $Q_{in}=+20.9\ {\rm J}$ . First from the definition of the work done on the gas find $W_{on}$, then use the 2${}^{nd}$ law of thermodynamics as $\Delta U_{int}=Q_{in}+W_{on}$ to determine the $\Delta U_{int}$.
\[W_{on}=-P\left(V_2-V_1\right)=-\left(1\times 1.01\times {10}^5{\rm Pa}\right)\left({\rm 100-50}\right)\left({{\rm 10}}^{{\rm -}{\rm 6}}{{\rm m}}^{{\rm 3}}\right){\rm =-5.05\ J}\]
\[\Delta U_{int}=+20.9+\left(-5.05\right)=+15.85\]
(b) Molar specific heat of the gas at constant pressure is defined by $C_P=\frac{1}{n}\frac{\Delta Q}{\Delta T}$ so first find the temperatures of the gas at the given points as
\[T_1=\frac{P_1V_1}{nR}=\frac{\left(1.01\times {10}^5\right)\left(50\times {10}^{-6}\right)}{\left(2\times {10}^{-3}\right)\left(8.314\right)}=303.7\ {\rm K}\]
\[T_2=\frac{P_2V_2}{nR}=\frac{\left(1.01\times {10}^5\right)\left(100\times {10}^{-6}\right)}{\left(2\times {10}^{-3}\right)\left(8.314\right)}=607.4\ {\rm K}\]
Therefore,
\[C_P=\frac{1}{n}\frac{Q_{in}}{T_2-T_1}=\frac{1}{0.002}\left(\frac{20.9}{607.4-303.7}\right)=34.4\frac{{\rm J}}{{\rm mol.K}}\]
(c) Similarly, Molar specific heat of the gas at constant volume is defined by
\[C_V=\frac{1}{n}\frac{\Delta U_{int}}{\Delta T}\]
\[\therefore C_V=\frac{1}{0.002}\left(\frac{15.85}{607.4-303.7}\right)=26.09\ \frac{{\rm J}}{{\rm mol.K}}\]
A Carnot engine operates between $235{\rm{}^\circ\,\!C}$ and $115{\rm{}^\circ\,\!C}$, absorbing $6.30\times {10}^4{\rm J}$ per cycle at the higher temperature.
(a) What is the efficiency of the engine?
(b) How much work per cycle is this engine capable of performing?
(a) Recall that the efficiency of a Carnot engine is given by 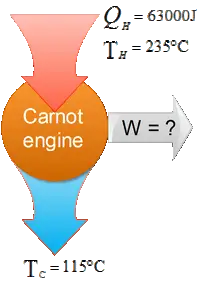
\begin{gather*} e=\frac{W_{net}}{Q_h} \\ {\rm or\ \ } \\ e=1-\frac{\left|Q_c\right|}{\left|Q_h\right|}\ \ \ \ \ {\rm or} \\ e=1-\frac{T_c}{T_h}\end{gather*}
Here, engine takes $Q_h$ from the hot reservoir at temperature $T_h$, does work $W_{net}$ and release $Q_c$ to the cold reservoir at $T_c$.
Therefore, \begin{align*} e&=1-\frac{115{\rm{}^\circ\,\!C}+273}{235{\rm{}^\circ\,\!C}+273} \\& =1-\frac{388}{508}\\&=23.6 \% \end{align*}
Note: temperatures must be in Kelvins.
(b) Use the first equation to find the work done by the engine
\begin{align*}W_{net}&=eQ_h\\&=23.6\times {10}^{-2}\times 6.3\times {10}^4\\ &=14.9\quad {\rm kJ}\end{align*}
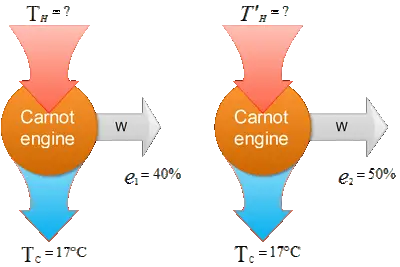
A Carnot engine whose low temperature reservoir is at $17{\rm{}^\circ\,\!C}$ has an efficiency of $40\%$. By how much should the temperature of the high temperature reservoir be increased to increase the efficiency to $50\%$?
The efficiency of a heat engine is defined as the ratio of the work done by the engine to the heat absorbed from the high-temperature reservoir i.e. $e=W/Q_h$. So
Given data: $T_c=17{\rm{}^\circ\,\!C}+273=290{\rm K\ ,\ \ }{{\rm e}}_{{\rm 1}}{\rm =40\%\ \ \ ,\ \ }{{\rm e}}_{{\rm 2}}{\rm =50\%}$
\[e_1=1-\frac{T_c}{T_h}\Rightarrow T_h=\frac{T_c}{1-e_1}=\frac{290}{1-0.40}=483.3\ {\rm K}\]
\[T^{'}_h=\frac{T_c}{1-e_2}=\frac{290}{1-0.50}=580\ {\rm K}\]
\[\Delta T=T^{'}_h-T_h=96.7\ {\rm K}\]
An ideal gas undergoes a reversible isothermal expansion at $77{\rm{}^\circ\,\!C}$. Increasing its volume from $1.30\ {\rm L}$ to $3.40\ {\rm L}$. The entropy change of the gas is $22\ {\rm J/K}$. How many moles of gas are present?
Note: the work done on the gas in an isothermal expansion is given by $W_{on}=-nRT{\ln \left(\frac{V_f}{V_i}\right)\ }$ and its change in internal energy ($\Delta U_{int}=nC_V\Delta T$) is zero since $\Delta T=0$. So use the first law of thermodynamics to find the heat absorbed by the gas and then use the definition of entropy change to find its value.
\[\Delta U_{int}=W_{on}+Q_{in}\Rightarrow Q_{in}=-W_{on}=nRT\,{\ln \left(\frac{V_f}{V_i}\right)\ }\]
The change in entropy of a system as it goes from one state to another is defined as $\Delta S=\Delta Q_{in}/T$ where $\Delta Q_{in}$ is the heat absorbed by the system in a reversible process.
\[\Rightarrow \Delta S=\frac{nRT\,{\ln \left(\frac{V_f}{V_i}\right)\ }}{T}=nR\,{\ln \frac{V_f}{V_i}\ }\]
\[\Rightarrow \ \ n=\frac{\Delta S}{R\left({\ln \frac{V_f}{V_i}\ }\right)}=\frac{22}{8.314\times {\ln \left(\frac{3.4}{1.3}\right)\ }}=2.75\ {\rm mol}\]
Four moles of an ideal gas undergo a reversible isothermal expansion from volume $V_1$ to volume $V_2=2V_1$ at temperature $T=400\ {\rm K}$. Find:
(a) The work done by the gas
(b) The entropy change of the gas
(c) If the expansion is reversible and adiabatic instead of isothermal, what is the entropy change of the gas?
(a) The work done by the gas in an isothermal process is $W=nRT\,{\ln \frac{\displaystyle V_f}{\displaystyle V_i}\ }$, so
\[W_{by}=4\left(8.314\right)\left(400\right){\ln \left(\frac{2V_1}{V_1}\right)\ }\ \sim \ 9220\ {\rm J}\]
(b) The entropy change of a system is $\Delta S=\Delta Q_{in}/T$, so use the first law of thermodynamics to find the heat absorbed by the gas as
\[{\left(\Delta U_{int}\right)}_{isothermal}=W_{on}+Q_{in}=0\Rightarrow Q_{in}=-W_{on}\]
Recall that the work done on the gas is equal to the minus of the work done by the gas i.e. $W_{on}=-W_{by}$, thus $Q_{in}=-W_{on}=W_{by}$
\[\Delta S=\frac{W_{by}}{T}=\frac{nRT\,{\ln 2\ }}{T}=nR\,{\ln 2\ }=\left(4\right)\left(8.314\right){\ln 2\ }=+23.05\frac{{\rm J}}{{\rm K}}\]
(c) In adiabatic processes the heat exchange is zero i.e. no heat transfers into or out of the system, $Q_{in}=Q_{out}=0$ so using the definition of the entropy change we have
\[\Delta S=\frac{\Delta Q_{in}}{T}=0\]
This is always true for any reversible adiabatic process.
A total work of $1590\ {\rm J}$ is applied to a moveable piston which causes the volume in a cylinder to contract. Assume this cylinder is filled with $84.6\ {\rm mol}$ of an ideal gas, which remains isobaric at a pressure of $8.6\ {\rm atm}$ as the piston moves. If the initial temperature of the gas is $12.6{\rm{}^\circ\,\!C}$, what is the final temperature of the gas (in ${\rm{}^\circ\,\!C}$) after the work is performed?
From the equation of state of an ideal gas, we have $P\Delta V=nR\Delta T$ combine this with the definition of the work done on the gas i.e. $W_{on}=-P\Delta V$ to find the desired temperature.
\[W_{on}=-P\Delta V=-1590\ {\rm J}\]
Since the volume is contracted so the work done on the gas, by convention, is negative i.e. $-1590\ {\rm J}$.
\[P\Delta V=nR\Delta T\to \ -W=nR\left(T_f-T_i\right)\ \]
\begin{align*}\Rightarrow T_f&=-\frac{W}{nR}+T_i\\ &=-\frac{-1590}{\left(84.6\right)\left(8.314\right)}+\left(273+12.6{\rm{}^\circ\,\!C}\right)\\ &=287.86\ {\rm K}\end{align*} Use the relation $T\left(K\right)=273+T\left({\rm{}^\circ\,\!C}\right)$ to convert Kelvins to Celsius as \[ \Rightarrow T\left({\rm{}^\circ\,\!C}\right)=287.86-273=14.86\ {\rm{}^\circ\,\!C} \]
A quantity of neon gas (ideal and monoatomic) is compressed adiabatically in an insulated container from $0.200\ {{\rm m}}^{{\rm 3}}$ to $0.100\ {{\rm m}}^{{\rm 3}}$. The original pressure is $2.00\times {10}^5\ {\rm Pa}$.
(a) What is the final pressure?
(b) The final temperature of the neon gas is $305\ {\rm K}$. What is the initial temperature?
(c) What is the rms speed of the neon atoms in the final state? The mass of a single neon atom is $3.35\times {10}^{-26}\ {\rm k}{\rm g}$.
(d) How much does the internal energy of the gas change in this compression?
(e) How much work is done by the gas during this change?
(a) In a adiabatic process, we have $PV^\gamma={\rm Constant}$. Where $\gamma$ is the ratio of the heat capacities i.e. $\gamma=C_P/C_V$. So between initial and final states we have $P_iV^\gamma_i=P_fV^\gamma_f$
\begin{align*} \Rightarrow P_f&=P_i{\left(\frac{V_i}{V_f}\right)}^\gamma\\ &=\left(2\times {10}^5\right){\left(\frac{0.2}{0.2}\right)}^{\frac{5}{3}}\\ &=6.34\times {10}^5\ {\rm Pa}\end{align*}Recall that in the monatomic case $C_V=\frac{3}{2}R\ $and $C_P=C_V+R=\frac{5}{2}R$.
(b) One of the other relations for an adiabatic process is $TV^{\gamma-1}={\rm Constant}$. Using this between initial and final points $T_iV^{\gamma-1}_i=T_fV^{\gamma-1}_f$ we have
\begin{align*} \Rightarrow T_i&=T_f{\left(\frac{V_f}{V_i}\right)}^{\gamma-1}\\ &=305{\left(\frac{0.1}{0.2}\right)}^{\frac{5}{3}-1}\\ &=192.13\ {\rm K} \end{align*}
(c) The rms speed of a molecule of a gas is related to the absolute temperature by
\[v_{rms}=\sqrt{\frac{3RT}{M}}\quad {\rm or}\quad v_{rms}=\sqrt{\frac{3kT}{m}}\]
Where $M$ is the molar mass of the molecule and $m$ is the mass of the molecule.
\[v_{rms}=\sqrt{\frac{3kT}{m}}=\sqrt{\frac{3\times 1.381\times {10}^{-23}\times 305}{3.35\times {10}^{-26}}}=614.16\frac{{\rm m}}{{\rm s}}\]
(d) The change in the internal energy of a system is given by $\Delta U_{int}=nC_V\Delta T$ that for an ideal monatomic gas is $\Delta U_{int}=\frac{3}{2}nR\Delta T$. Therefore, first compute the number of moles i.e. $n$ as
\begin{gather*} P_iV_i=nRT_i\\ \Rightarrow \left(2\times {10}^5\right)\left(0.2\right)=n\left(8.314\right)\left(192.13\right)\\ \Rightarrow n=25.04\ {\rm mole} \end{gather*} Now substitute $n$ in the definition of the internal energy
\begin{align*} \Delta U_{int}&=\frac{3}{2}nR\left(T_f-T_i\right)\\ &=\frac{3}{2}\left(25.04\right)\left(8.314\right)\left(305-192.13\right)\\ &=3.52\times {10}^4\ {\rm J} \end{align*}
(e) Since the heat exchange in an adiabatic process is zero i.e. $Q_{in}=0$ use first law of thermodynamics to find the work done by the gas
\[\Delta U_{int}=W_{on}+Q_{in}\Rightarrow \Delta U_{int}=W_{on}\]
By convention, $W_{on}=-W_{by}$, thus
\[\Delta U_{int}=-W_{by}\]
\[\therefore \ W_{by}=-3.52\times {10}^4{\rm \ J}\]
The negative sign indicates that the work is done by an external agent on the gas to compress it.
A Carnot cycle is given as shown in the figure.AB and CD are isothermal with 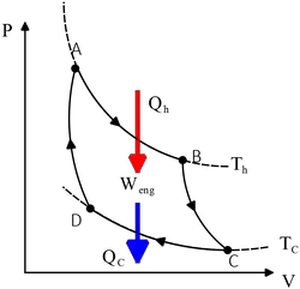 $T_h=500{\rm ^\circ C}$ and $T_c=100{\rm ^\circ C}$.BC and DA are adiabatic. The heat going into the cycle $Q_h$ is $2000\,{\rm J}$.
$T_h=500{\rm ^\circ C}$ and $T_c=100{\rm ^\circ C}$.BC and DA are adiabatic. The heat going into the cycle $Q_h$ is $2000\,{\rm J}$.
(a) Find the heat $Q_c$ leaving the cycle.
(b) Find the work done by the gas in a cycle.
(c) What is the efficiency of this cycle.
(a) We have an important relation for Carnot engine that relate temperatures and heat exchanges as 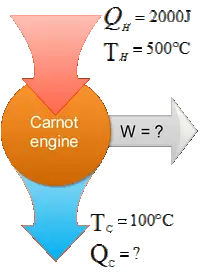
\[\frac{\left|Q_c\right|}{Q_h}=\frac{T_c}{T_h}\] Use this relation to find the heat $Q_c$ released to the cold reservoir.
\begin{align*} \frac{\left|Q_c\right|}{Q_h}=\frac{T_c}{T_h} \\ \Rightarrow \left|Q_c\right|&=Q_h\frac{T_c}{T_h}\\&=2000\, \left(\frac{100+273}{500+273}\right)\\&=965.1\quad {\rm J\ }\end{align*} \[\Rightarrow Q_c=-965.1\quad {\rm J}\] We have inserted, by convention, a negative to indicate that the heat leaves the cycle.
(b) In the Carnot engines (cycles) from first law of thermodynamics, we have
\begin{gather*}W_{net}+\left|Q_c\right|=Q_h \\ \\ \Rightarrow W_{net}=2000-965.1=1034.9\quad{\rm J}\end{gather*}
Where $W_{net}$ is the work done by the engine.
(c) The efficiency of an Carnot engine is given by
\[e=1-\frac{T_c}{T_h}=1-\frac{373}{773}=0.517=51.7\%\]
Consider the frictionless piston system below where gravity is pointing downwards and outside of the piston-gas system is vacuum.The piston mass is $M_p$ and its cross sectional area is $A$. The gas is ideal.
outside of the piston-gas system is vacuum.The piston mass is $M_p$ and its cross sectional area is $A$. The gas is ideal.
(a) Suppose the piston is initially held by hand at a certain initial height, and the initial pressure of the gas at that point is $P_1$. Subsequently, the piston is released and allowed to fall. Write down an inequality expression involving $M_p$ , $A$, $P_1$ , and $g$ which is necessary for the piston to fall. Express your answer in the form ``$P_1<\ \dots .$''.
(b) Suppose during the fall depicted in part (a), heat is drawn out of the gas such that the gas maintains a constant temperature as the piston falls. If the initial height of the piston is $h$, what is the final height of the piston? [Express your final answer in terms of $M_p$ , $A$, $P_1$ , $g$, and $h$.]
(a) To piston fall freely, its weight must be greater than the force provided by the pressure $P_1$ that is $F_1=P_1A$. Therefore,
\[W>F_1\Rightarrow M_Pg>P_1A\]
\[\ \therefore \ P_1<\frac{M_pg}{A}\]
(b) When the force produced ($F_2=P_2A$) by the pressure at later time balanced with the weight of the piston, the system reaches the final equilibrium state, that is $M_pg=P_2A$. Use the ideal gas law $PV=nRT$ between initial and final states to find the final height $h_2$.
\[P_1V_1=Nk_BT=P_2V_2\ {\rm since\ temperature\ is\ constant}\]
\[P_1Ah=P_2Ah_2\]
\[\therefore h_2=\frac{P_1A}{P_2A}h=\frac{P_1A}{M_Pg}h\]
In the last line, we have used the final equilibrium condition.
A projectile with mass ${\rm m}$ can ''escape'' from the surface of a planet if it is launched vertically upward with kinetic energy greater than $mgR_p$ where ${\rm g}$ is the acceleration due to the gravity at the planet's surface and ${{\rm R}}_{{\rm p}}$ is the planet's radius. Ignore the air resistance.
(a) If the planet in the question is the earth, at what temperature does the average translational kinetic energy of the nitrogen molecule (molar mass $28.0\ {\rm g/mol}$) equal that required to escape the earth? What about the hydrogen molecule (molar mass $2.0\ {\rm g/mol}$), $g=9.8\ {\rm m/}{{\rm s}}^{{\rm 2}}$ , $R_E=6380\ {\rm km}$
(c) Repeat part (a) for the moon, which has $g=1.63\ {\rm m/}{{\rm s}}^{{\rm 2}}$ and $R_M=1740\ {\rm km}$. The moon and earth have similar surface temperatures, but the moon has no atmosphere and the earth has no $H_2$ in the atmosphere! Why is this the case?
(c) Repeat part (a) for the sun, which has $g=274.2\ {\rm m/}{{\rm s}}^{{\rm 2}}$ and $R_s=6.96\times {10}^5\ {\rm km}$. What does this say about escaping the sun, especially for those fleet-footed $H_2$ molecules? The surface temperature of the sun is 5800 K.
(a) Average kinetic energy ($\bar{K}$) of a molecule with temperature $T$ is $\bar{K}=\frac{3}{2}k_BT$ so for $N_A$ molecules have: \[N_A\underbrace{\left({\frac{1}{2}mv^2}\right)}_{\bar{K}}=\frac{3}{2}N_Ak_BT=\frac{3}{2}RT\] where $mN_A=M$ is the molar mass.
The criteria for the escape of $N_A$ molecules from the surface of a planet is stated as the kinetic energy $\ge$ potential energy
\[ \frac{3}{2}RT\ge \left(N_Am\right)gR_P\Rightarrow T>\frac{2N_AmgR_P}{3R}\]
Thus the minimum temperature achieved by $N_2$ is \[T_{N_2}=\frac{2(N_Am)gR_E}{3R}=\frac{2MgR_E}{3R}\] Substituting the numerical values into it, gives \begin{align*} T_{N_2}&=\frac{2\times 28\times {10}^{-3}\times 9.8\times 6.38\times {10}^6}{3\times 8.31} \\\\ &=1.4\times {10}^5\,\rm K \\\\ \Rightarrow \quad T_{H_2}&=\frac{2}{28}T_{N_2}\\\\& =1\times {10}^4{\rm K} \end{align*}
(b) First, find the ratio of $gR$ on the moon to the earth, and then substitute it into the minimum temperature achieved by a molecule to escape the surface.\begin{align*} \frac{g_MR_M}{g_ER_E}&=\frac{(1.63)(1740)}{(9.8)(6380)} \\\\ &=4.53\times {10}^{-2} \\\\ T_{N_2}&=\frac{2Mg_MR_M}{3R} \\\\&=\left(4.53\times {10}^{-2}\right)\frac{2Mg_ER_E}{3R} \end{align*} Therefore, the temperature required to escape $N_2$ molecules off the surface of the moon is \[T_{N_2}=4.53\times {10}^{-2}\left(1.40\times {10}^5\right)=6.35\times {10}^3\, {\rm K}\] and with similar calculation for $H_2$ is \[T_{H_2}=4.53\times {10}^{-2}\left(1\times {10}^4\right)=453\ {\rm K}\]
At a given temperature, the escape temperatures of $N_2$ and $H_2$ for the moon are much less than for the earth.
(c) Similar to the previous, \[\frac{g_sR_s}{g_ER_E}=\frac{\left(274.2\right)\left(6.96\times {10}^5\right)}{\left(9.8\right)\left(6380\right)}=3.06\times {10}^3\]
\[T_{N_2}=\left(3.06\times {10}^3\right)\left(1.4\times {10}^5\right)=4.28\times {10}^8\ {\rm K}\]
\[T_{H_2}=\left(3.06\times {10}^3\right)\left(1\times {10}^4\right)=3.06\times {10}^7\ {\rm K}\]
Sun is too big and not hot enough to provide temperature for escaping:
Ratio is $\frac{3.06\times {10}^7}{5800}=5.27\times {10}^3$. Almost nothing escapes.
A heat engine takes $0.350\ {\rm moles}$ of a diatomic ideal gas around the cycle 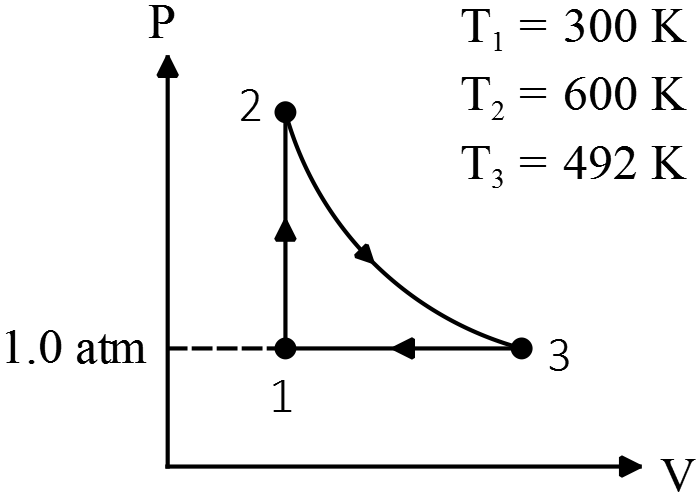 shown in the PV diagram. Process $1\to 2$ is at constant volume $V$ and process $2\to 3$ is adiabatic, and process $3\to 1$ is at a constant pressure P of $1.00\ {\rm atm}$. The value of $?$ for this gas is 1.4
shown in the PV diagram. Process $1\to 2$ is at constant volume $V$ and process $2\to 3$ is adiabatic, and process $3\to 1$ is at a constant pressure P of $1.00\ {\rm atm}$. The value of $?$ for this gas is 1.4
(a) Find the pressure and volume at points 1,2 and 3.
(b) Calculate $Q\ ,\ W$ and $\Delta U$ for each of the three processes.
(c) Find the net work done by the gas in the cycle.
(d) Find the net heat flow into the engine in one cycle, use this result to calculate the thermal efficiency of this engine, and how it compares with the efficiency of a Carnot engine operating between the same $T_1$ and $T_2$?
Note: in an diatomic gas, we have $C_V=\frac{5}{2}R$ and $C_P=C_V+R=\frac{7}{2}$
(a) First, use the equation of state of ideal gas to find the volume of point 1:
\[PV=nRT\to V_1=\frac{nRT_1}{P_1}=\frac{\left(0.350\right)\left(8.31\right)\left(300\right)}{1.01\times {10}^5}=8.62\times {10}^{-3}\ {{\rm m}}^{{\rm 3}}\]
Since in diagram $V_1=V_2$ use the ideal gas law between theses points to find the $P_2$.
\[\frac{P_2V_2}{T_2}=\frac{P_1V_1}{T_1}\to \frac{P_2}{T_2}=\frac{P_1}{T_1}\ \Longrightarrow P_2=\frac{600}{300}\times 1.01\times {10}^5=2\ {\rm atm}\]
Process $1\to 3$ is isobar that is $P_1=P_3$, use again the ideal gas law between them
\[\frac{{P_3V}_3}{T_3}=\frac{P_1V_1}{T_1}\ \ \Longrightarrow V_3=\frac{492}{300}\times \left(8.62\times {10}^{-3}\right)=14.1\times {10}^{-3}\ {{\rm m}}^{{\rm 3}}\]
(b) We know, by definition, the work done on the system is $W_{on}=-P\Delta V$ ,
In $1\to 2$ : $\Delta V=0\ \Longrightarrow W_{1\to 2}=0$
$Q_{1\to 2}=nC_V\Delta T=0.35\times 20.79\times \left(600-300\right)=+2180\ {\rm J}$. Since its value is positive, so by convention, heat flows into the engine. Now use the first law of thermodynamics to find the change in internal energy of the gas.
\[{\left(\Delta U_{int}\right)}_{1\to 2}={\left(Q_{in}\right)}_{1\to 2}+{\left(W_{on}\right)}_{1\to 2}=+2180\ {\rm J}\]
In $2\to 3$:
In an adiabatic process heat exchange is zero so, $Q_{in-out}=0$
\[\Delta U_{int}=nC_V\Delta T=\left(0.35\right)\left(20.79\right)\left(492-600\right)=-780{\rm J}\]
\[\Delta U_{int}=Q_{in}+W_{on}\to W_{on}=\Delta U_{int}-Q_{in}=-780\ {\rm J}\]
In $3\to 1$:
Isobar process so,
\[W_{on}=-P\Delta V=-\left(1.01\times {10}^5\right)\left(8.62-14.1\right)\times {10}^{-3}=+560\ {\rm J}\]
\[Q_{in}=nC_P\Delta T=\left(0.35\right)\left(29.11\right)\left(300-492\right)=-1960\ {\rm J}\]
\[\Delta U_{int}=Q_{in}+W_{on}=-1960+\left(+560\right)=-1400\ {\rm J}\]
Since $Q_{in}<0$, so some heat transferred into the surrounding.
(c) In each cycle the total internal energy of a system is zero since $\Delta U_{int}=nC_V\Delta T=\Delta Q_{in}{\rm +}\Delta W_{on}$ And $\Delta {\rm T=0}$ (we have come back to the initial position!), then $\Delta U_{int}=0$and $\Delta Q_{in}=-\Delta W_{on}$. Therefore, the work done on the gas and heat transferred into the system is as follows
\[W_{net\ on}=W_{1\to 2}+W_{2\to 3}+W_{3\to 1}=0-780+560=-220\ {\rm J}\]
\[Q_{net\ in}=Q_{1\to 2}+Q_{2\to 3}+Q_{3\to 1}=2180+0-1960=+220\ {\rm J}\]
In general, the work done by the gas is the negative of the work done on the gas so
\[W_{on}=-W_{by}\Rightarrow W_{by}=+220\ {\rm J}\]
(d) By convention, if $Q>0$ , then heat transferred into the system. In this problem, only $Q\left(1\to 3\right)>0$, so the net heat flows into the engine is $Q_{in}=2180\ {\rm J}$. The thermal efficiency of a heat engine is defined as the ratio of the net work done by the engine during one cycle to the heat transferred into it at higher temperature during the cycle. Therefore,
\[e=\frac{W_{net}}{Q_H}=\frac{+220}{2180}=0.101\ \sim \ 10.1\%\]
The Carnot engine is the most efficient heat engine that works between $T_h$ and $T_c$ and its efficiency is defined as
\[e_{Carnot}=1-\frac{T_c}{T_H}=1-\frac{300}{600}=0.5=50\%\]
As expected $e_{Carnot}>e$.
You build a heat engine that takes ${\rm 1.00\ mol}$ of an ideal diatomic gas through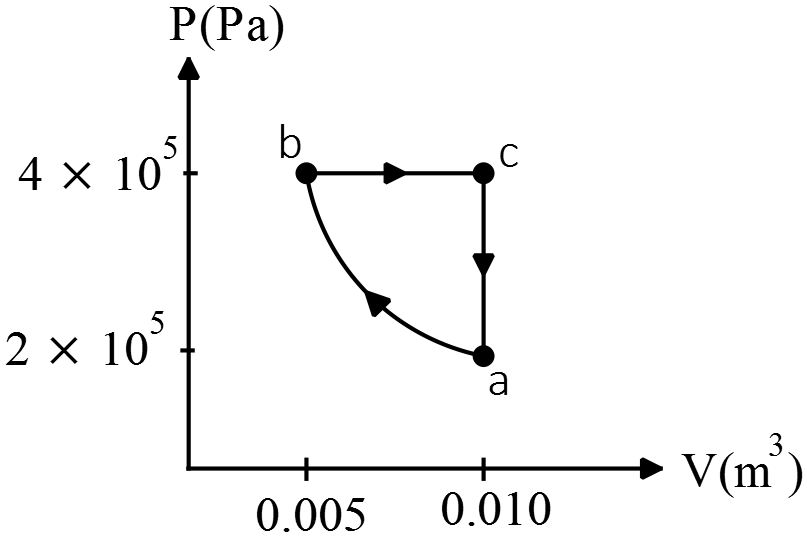 the cycle shown. ($C_V=\frac{5}{2}R\ ,\ C_P=\frac{7}{2}R$)
the cycle shown. ($C_V=\frac{5}{2}R\ ,\ C_P=\frac{7}{2}R$)
(a) Show that the path or segment $ab$ is an isothermal compression.
(b) During which segment of the cycle is the heat absorbed by the gas? During which segment of the cycle is heat rejected by the gas? How do you know this?
(c) Calculate the temperatures at points $a,b$ and $c$.
(d) Calculate the net heat exchanged with the surrounding heat reservoirs, and the net work done by the engine in one cycle, and calculate the thermal efficiency of the engine
(a) In an isothermal process, temperatures between two points are the same. So use the ideal gas law $PV=nRT$ to find $T_a$ and $T_b$.
\[T_a=\frac{P_aV_a}{nR}=\frac{\left(2\times {10}^5\right)\left(0.01\right)}{\left(1\right)\left(8.314\right)}=240.55\ {\rm K}\]
\[T_b=\frac{P_bV_b}{nR}=\frac{\left(4\times {10}^5\right)\left(0.005\right)}{\left(1\right)\left(8.314\right)}=240.55\ {\rm K}\]
Since $T_a=T_b$ so the path $b\to a$ is an isothermal process.
(b) Use the definitions of heat transferred $Q=nC_{V,P}\Delta T$ and work done on the system $W_{on}=-P\Delta V$ to find desired values. Path $ab$ is isothermal. Using first law of thermodynamics $\Delta U_{int}=W_{on}+Q_{in}$ we know that $\Delta U_{int}=0$ so $Q_{in}=-W_{on}=nRT{\ln \frac{V_b}{V_a}\ }\ \ ,\ \ V_a>V_b\ \Longrightarrow \ \ Q_{in}<0$ so heat is rejected.
In $bc$ process $P$ is constant, so $=nC_P\Delta T$ , use the ideal gas law to substitute $\frac{P\Delta V}{R}$ for $n\Delta T$ so $Q=\frac{C_P}{R}P\Delta V$. Since $\Delta V=\left(V_c-V_a\right)>0$ so $Q>0$ and subsequently heat is absorbed.
In $ca$ process $V$ is constant (isochoric process), so $Q=nC_V\Delta T=\frac{C_V}{R}V\Delta P\ ,\ \Delta P<0\ \Longrightarrow Q<0\ $so heat is rejected.
(c) \[T_a=T_b=\frac{P_aV_a}{nR}=\frac{2\times {10}^3}{1\times 8.314}=240.55\ {\rm K}\]
\[T_c=\frac{P_cV_c}{nR}=\frac{4\times {10}^3}{1\times 8.314}=481.11\ {\rm K}\]
(d) In part (c) we have find the temperatures of points, so
\[Q_{bc}=nC_P\Delta {{\rm T}}_{{\rm bc}}{\rm =}\left({\rm 1.0}\right)\left(\frac{{\rm 7}}{{\rm 2}}\right)\left({\rm 8.134}\right)\left({\rm 481.11-240.55}\right){\rm =7.00\times }{{\rm 10}}^{{\rm 3}}\ {\rm J}\]
\[Q_{ca}=nC_V\Delta T_{ca}=\left(1.0\right)\left(\frac{5}{2}\right)\left(8.314\right)\left(240.55-481.11\right)=-5.00\times {10}^3{\rm J}\]
\[Q_{ab}=nRT{\ln \left(\frac{V_b}{V_a}\right)\ }=\left(1.0\right)\left(8.314\right)\left(240.55\right){\ln \left(\frac{0.005}{0.01}\right)\ }=-1.38\times {10}^3\ {\rm J}\]
\[\therefore Q_{total}=+620\ {\rm J}\]
The path $ab$ is isothermal that is $\Delta U_{int}=\frac{3}{2}nR\Delta T={{\rm Q}}_{{\rm in}}{\rm +}{{\rm W}}_{{\rm on}}{\rm =0}$ ,thus the work done on the gas is ${\left(W_{on}\right)}_{ab}=-{\left(Q_{in}\right)}_{ab}=+1.38\times {10}^3\ {\rm J}$. By convention, the work done by the gas is ${(W_{by})}_{ab}=-1.38\times {10}^3{\rm J}$.
\[{\left(W_{on}\right)}_{bc}=-P\Delta V=-\left(4\times {10}^5\right)\left(0.01-0.005\right)=-2000\ {\rm J}\]
\[{\left(W_{on}\right)}_{ca}=-P\Delta V=0\]
\[\therefore {\left(W_{on}\right)}_{net}=1380{\rm -}{\rm 2000=-620}\ {\rm J\ and\ }{\left(W_{by}\right)}_{net}{\rm =+620\ J}\]
\[e=\frac{{\left(W_{by}\right)}_{net}}{Q_H}=\frac{620}{7.01\times {10}^3}=8.84\ \%\]
You have two identical containers, one containing gas A and the other gas B. the masses of these molecules are $m_A=3.3\times {10}^{-27}{\rm kg}$ and $m_B=5.34\times {10}^{-26}{\rm kg}$. Both gases are under the same pressure and are at temperature $T=10{\rm C{}^\circ\, =283\ K}$
(a) Which molecules, A or B have the greatest translational kinetic energy, and which molecules have the greatest ${\rm rms}$ speed $v_{rms}$? Recall the $v_{rms}={\left(\frac{3kT}{m}\right)}^{\frac{1}{2}}$
(b) Which container's temperature A or B should you raise so that both gasses will have the same rms speed $v_{rms}$.
(c) At what temperature will you accomplish this goal? Now which molecule A or B has the greatest translational energy?
(d) For part (c) what is the most probably speed $v_{mp}$ and what is the average speed $v_{ave}$ for the gas with the greatest energy. $v_{mp}={\left(\frac{2kT}{m}\right)}^{\frac{1}{2}}$, and $v_{ave}={\left(\frac{8kT}{pm}\right)}^{\frac{1}{2}}$.
(a) The translational kinetic energy of a monoatomic molecule such as ($H_2,N_2,\dots )$ is $K_{tr}=\frac{1}{2}m\overline{v^2}$ where $\overline{v}$ is the average velocity of the it. This molecule can move in three direction ($x,y,z$) or have three degrees of freedom (DOF). By Equipartition theorem, each of the DOF contributes $\frac{1}{2}k_BT$ to the kinetic energy. therefore, the total translational kinetic energy of $n$ moles of a gas containing $N$ molecules is
\[K_{tr-ave}=N\left(\frac{1}{2}m\overline{v^2}\right)=N\left(\frac{3}{2}k_BT\right)=\frac{3}{2}nRT\]
Where we have used $Nk_B=nN_Ak_B=nR$. ($N_A$ is Avogadro's number). In other words, the absolute temperature is a measure of the translational kinetic energy of the molecules. Since container A and B have the same $T$ so $K_{tr-A}=K_{tr-B}$. In the above equation, the square root of $\overline{v^2}$ is an estimation of the order of magnitude of the speeds of the molecules in the gas, that can be determined by $v_{rms}=\sqrt{\overline{v^2}}=\sqrt{\frac{3RT}{M}}=\sqrt{\frac{3k_BT}{m}}$, where $M=N_Am$ is the molar mass of the molecules. because $v_{rms}\propto \ 1/\sqrt{m}$ and $m_A>m_B$ therefore, the lightest molecule (A) has the greatest $rms$ speed.
(b) Since B is heavier, we need to raise its energy to get the same $v_{rms}$ as A.
(c) We want ${\left(v_{rms}\right)}_A={\left(v_{rms}\right)}_B$
\[\sqrt{\frac{3k_BT_A}{m_A}}=\sqrt{\frac{3k_BT_B}{m_B}}\Rightarrow T_B=\frac{m_B}{m_A}T_A=\frac{5.34\times {10}^{-26}}{3.34\times {10}^{-27}}\left(283\right)=4531\ {\rm K}\]
Therefore, we must raise the temperature of the container B to $4531\ {\rm K}$ so that both of them have the same rms speed. Since translational kinetic energy only depends on the absolute temperature, so the B molecules have the greatest translational energy.
(d) \[v_{rms}=\sqrt{\frac{3kT}{m}}=\sqrt{\frac{3\left(1.38\times {10}^{-23}\right)\left(4531\right)}{5.34\times {10}^{-26}}}=1874\frac{{\rm m}}{{\rm s}}\]
\[v_{mp}=\sqrt{\frac{2}{3}}v_{rms}=0.816\times 1874=1529\frac{{\rm m}}{{\rm s}}\]
\[v_{ave}=\sqrt{\frac{8}{3p}}v_{rms}=0.92\times 1874=1724\frac{{\rm m}}{{\rm s}}\]
The figure shows a $pV$ diagram for an ideal gas in which its absolute temperature at $b$ is one-fourth of its absolute temperature at $a$.
(a) What volume does the gas occupy at point $b$?
(b) How many joules of work were done by or on the gas in the process?
(c) By how much did the internal energy $U$ of the gas change in going from state $a$ to $b$?
(d) By how much did the heat content of the gas change as it went from state $a$ to $b$?
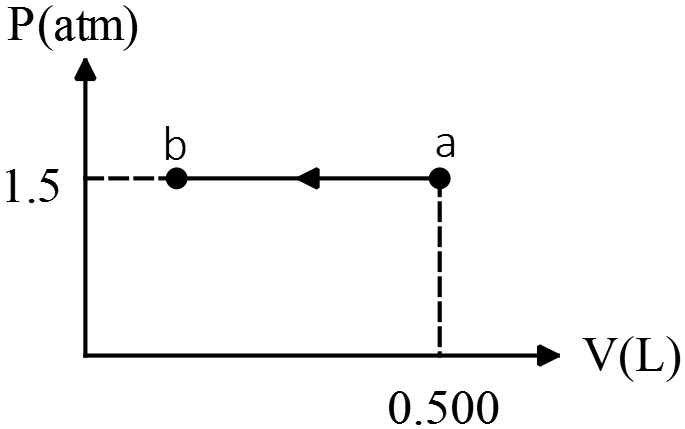
(a) Use the ideal gas law, $PV=nRT$ between a and b.
\[\frac{P_aV_a}{T_a}=\frac{P_bV_b}{T_b}\ \xrightarrow{a\to b\, \text{is isobar process}}\frac{V_a}{T_a}=\frac{V_b}{T_b}\]
\[\Rightarrow V_b=\frac{T_b}{T_a}\ V_a=\frac{1}{4}V_a\]
(b) External work done on the gas is defined as $W_{on}=-P\Delta V=-P\left(V_b-V_a\right)$
\begin{align*} W_{on}&=-P\left(\frac{1}{4}V_a-V_a\right)\\&=\frac{3}{4}PV_a\\&=\frac{3}{4}\ \left(1.5\ {\rm atm}\right)\left(0.5\ {\rm L}\right)\\&=+0.5625{\rm \ (lit.atm)}\end{align*}
In the SI units work must be in Joules, we know that ${\rm Pa.}{{\rm m}}^{{\rm 3}}={\rm J}$ so convert the above value as follows
\[+0.5625{\rm \ }\left({\rm lit.atm}\right){\rm =0.5625}\left({{\rm 10}}^{{\rm -}{\rm 3}}{\rm m^3}\right)\left(1.01\times {10}^5{\rm Pa}\right){\rm =56.81\ J}\]
Since $W>0$ so work done on the gas.
(c)
\begin{align*}U_{int}&=nC_V\Delta T=nC_V\left(T_b-T_a\right)\\&=nC_V\left(\frac{1}{4}-1\right)T_a\\&=-\frac{3}{4}nC_VT_a\\&=-\frac{3}{4}C_V\left(\frac{P_aV_a}{R}\right)\\ &=-\frac{3}{4}\left(\frac{3}{2}R\right)\left(1.5\times \left(1.01\times {10}^5{\rm Pa}\right)\right)\frac{\left(0.5\times {10}^{-3}\ {{\rm m}}^{{\rm 3}}\right)}{R}\\&=-85.85\ {\rm J}\end{align*}
In the third line, we have substituted $PV/R$ for $nT$ (from ideal gas law).
Note: for monoatomic gasses $C_V=\frac{3}{2}R$ and in general $C_P=C_V+R$
(d) From the first law of thermodynamics we have
\[\Delta U_{int}=Q_{in}+W_{on}\to Q_{in}=-85.85-56.81=-142.66\ {\rm J}\]
We are given $1/3$ of a mole of He gas, which is monoatomic. Calculate each of the following for the full path $a\to b\to c$.
(a) The work that is done.
(b) The change in internal energy.
(c) The heat added.
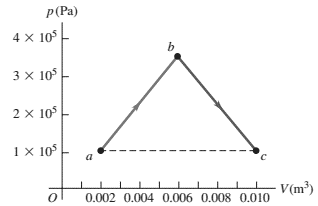
(a) In any process, the work done by the gas is the area under the $P-V$ diagram.
So we must find the sum of the area of triangle and rectangular.
\begin{align*} W_{by} &= S=S_{tri}+S_{rec}\\&=\frac{1}{2}\left(2\times {10}^5\right)\left(0.01-0.002\right)+\left(1\times {10}^5\right)\left(0.01-0.002\right)\\&=1000+800=1800\, {\rm J}\end{align*}
(b) The change in internal energy of a substance is independent of path and only depends on the initial and final temperature of the path. In general, we have $\Delta U_{int}=nC_V\Delta T$ where $C_V$ is the heat capacity at constant volume and for monoatomic molecules is equals to $\frac{3}{2}R$ per mole. So we must first determine the $T_a$ and $T_b$ by using the ideal gas law $PV=nRT$
\begin{align*}\Delta U_{int}&=\frac{3}{2}nR\left(T_c-T_a\right)\\&=\frac{3}{2}nR\left(\frac{P_cV_c}{nR}-\frac{P_aV_a}{nR}\right)\\&=\frac{3}{2}\left(P_cV_c-P_aV_a\right)\\ &=\frac{3}{2}\left(1\times {10}^5\right)\underbrace{\left(0.01-0.002\right)}_{0.008}\\&=1200\quad {\rm J}\end{align*}
(c) Use the first law of thermodynamics as $\Delta U_{int}=W_{on}+Q_{in}$ where $W_{on}$ is the work done on the gas and $Q_{in}$ is the heat transferred into it.
Note: recall that $W_{on}=-W_{by}$
\[\Rightarrow \Delta U_{int}=-W_{by}+Q_{in}\Rightarrow 1200=-1800+Q_{in}\]
\[\Rightarrow Q_{in}=+3000\ {\rm J}\] Since $Q_{in}>0$ so heat absorbed by the gas.
A piston expands using an ideal gas under constant pressure of ${\rm 5\ atm}$ from ${\rm 0.40\ L}$ to ${\rm 0.80\ L}$. Heat then flows out of the piston under constant volume. The pressure is allowed to drop until the temperature is the same as the original temperature.
(a) Draw a PV-diagram for the process above
(b) Calculate the total work done by the process above
(c) Calculate the total heat flow into the system. Hint: First calculate the change in internal energy and then use the first law of thermodynamics.
(a)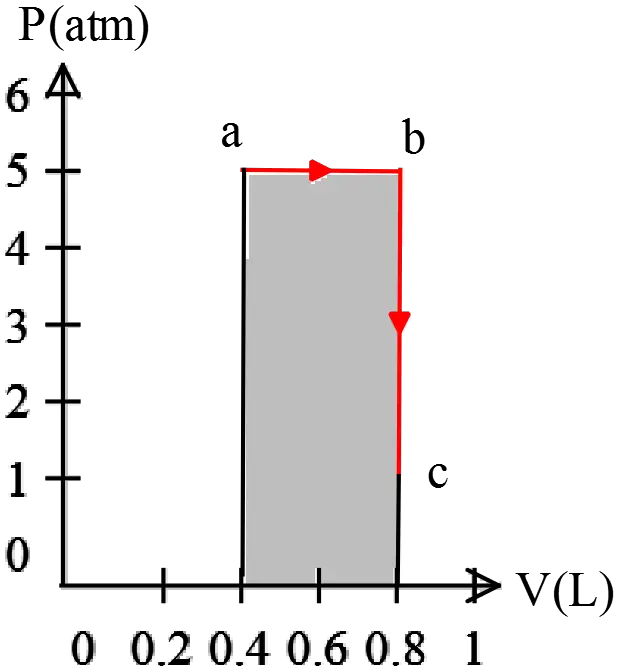
(b) The work done by an ideal gas is $W_{by}=P\Delta V$ where $P$ and $V$ must be in Pa and ${{\rm m}}^{{\rm 3}}$, respectively. ($1\ {\rm atm=1.01\times }{{\rm 10}}^{{\rm 5}}{\rm Pa\ ,\ 1lit=}{{\rm 10}}^{{\rm -}{\rm 3}}\ {{\rm m}}^{{\rm 3}}$)
\begin{align*}
W_{a\to b}&=5{\rm atm}\times \left(0.8-0.4\right){\rm lit}\\
&=\left(5\times 1.01\times {10}^5\right)\left(0.4\times {10}^{-3}\right)=202.6\ {\rm J}
\end{align*}
\[W_{b\to c}=0\ {\rm since}\ \Delta V=0\]
\[\therefore \ \ {\left(W_{by}\right)}_{tot}=W_{a\to b}+W_{b\to c}=202.6\ {\rm J}\]
Note that the work done on the gas is ${\left(W_{on}\right)}_{tot}=-P\Delta V=-202.6\ {\rm J}$
(c) First law of thermodynamics:
The change in the internal energy of a system equals the heat transfer into the system plus the work done on the system i.e. $\Delta U_{int}=Q_{in}+W_{on}$.
Note: the internal energy of an ideal gas is $U_{int}=\frac{3}{2}nRT$ i.e. depends only on the absolute temperature of the gas. Since at the final stage $c$, temperature is the same as initial stage $a$, Thus
\[\Delta U_{int}=\frac{3}{2}nR\left(T_f-T_i\right)=\frac{3}{2}nR\left(0\right){\rm =0}\]
\[{\left(\Delta U_{int}\right)}_{tot}={\left(Q_{in}\right)}_{tot}+{\left(W_{on}\right)}_{tot}=0\Rightarrow {\left(Q_{in}\right)}_{tot}=-{\left(W_{on}\right)}_{tot}\]
\[\therefore \ \ {\left(Q_{in}\right)}_{tot}=+202.6\ {\rm J}\]
Because $Q>0$ then heat transferred into the system.
An air mattress is inflated to a pressure of $110{\rm kPa}$(just a little above atmospheric pressure). When fully inflated, the mattress is $1.8\ {\rm m}$ long, $0.9\ {\rm m}$ wide and $15\ {\rm cm}$ thick. The mattress thickness gets decreased down to $13\ {\rm cm}$ when a person lies on it.
(a) If the length and width stay unchanged, what is the pressure of the air inside mattress when the person in lying on it?
(b) How many moles of air ($n$) are inside the mattress in part (a) if the temperature is $30{\rm{}^\circ\,\!C}$?
(a) Recall that the equation of state for an ideal gas is given by $PV=nRT$ where $n$ is the total mole of the substance and $R$ is the universal gas constant.
Note: if in a problem there are two states then we must use the equation below:
\[\frac{P_1V_1}{T_1}=\frac{P_2V_2}{T_2}\]
Now we have
\[\frac{P_1V_1}{T_1}=\frac{P_2V_2}{T_2}\ {\rm since\ T\ does\ not\ change\ so\ }P_1V_1=P_2V_2\]
\[110\times \left(1.8\times 0.9\times 0.15\right)=P_2\left(1.8\times 0.9\times 0.13\right)\]
\[P_2=\frac{110\times 0.15}{0.13}=126.92\ {\rm kPa}\]
(b) Using the equation of state
\[n=\frac{PV}{RT}=\frac{110\times {10}^3\times \left(1.8\times 0.9\times 0.15\right)}{8.315\times \left(273+30\right)}=10.6\ {\rm mol}\]
Note: in the equation of state $T$ is in kelvins.
One mole of a monoatomic ideal gas is taken through the cycle shown on the P-V diagram. Initially, the gas occupies a volume $V_1=16\times 10^{-3}\,{\rm m^3}$ at a pressure, $P_1=1.31\times 10^5\, {\rm Pa}$. it is expanded at constant pressure$(1\to 2)$ until the volume occupied is $V_2=24\times {10}^{-3}{{\rm m}}^{{\rm 3}}$. The gas is then compressed adiabatically $(2\to 3)$ until it occupies the original volume. The pressure in the gas is brought back to its original value by the isochoric process $(3\to 1)$. All processes are carried out slowly and reversibly.
(a) What is the temperature $T_2$ after the isobaric expansion $(1\to 2)$?
(b) What is the temperature $T_3$ after the adiabatic compression $(2\to 3)$?
(c) What is the heat absorbed by the gas $Q_{12}$ during the isobaric expansion $(1\to 2)$?
(d) Find the total work of the system?
(a) Use the ideal gas equation of state $PV=nRT$
\[\Rightarrow T_2=\frac{P_2V_2}{nR}=\frac{\left(1.31\times {10}^5\right)\left(24\times {10}^{-3}\right)}{1\left(8.314\right)}=378.15{\rm K}\]
(b) For adiabatic expansion and compression the ideal gas equation of state is as follows
\[PV^\gamma=Constant\quad {\rm or}\quad TV^{\gamma-1}=Constant\]
Where $\gamma$ is the ratio of the heat capacities $\gamma=C_P/C_V\ $
Therefore for the process ($2\to 3$) we have $T_2V^{\gamma-1}_2=T_3V^{\gamma-1}_3\Rightarrow T_3=T_2{\left(\frac{V_2}{V_3}\right)}^{\gamma-1}$
\[\Rightarrow \ \ T_3=378.15{\left(\frac{24\times {10}^{-3}}{16\times {10}^{-3}}\right)}^{\frac{5}{3}-1}=491.58\ {\rm K}\]
Note: the heat capacity at constant pressure and constant volume for an ideal monoatomic gas is $C_P=C_V+R=\frac{5}{2}nR$ and $C_V=\frac{3}{2}nR$, respectively.
(c) The amount of heat absorbed by the gas at constant volume or pressure is $Q_V=C_V\Delta T$ or $Q_P=C_P\Delta T$, respectively. First, find the temperature of point 1.
\[T_1=\frac{P_1V_1}{nR}=\frac{\left(1.31\times {10}^5\right)\left(16\times {10}^{-3}\right)}{\left(1\right)\left(8.314\right)}=252.1\]
\[Q_{1\to 2}=C_P\Delta T=\frac{5}{2}nR\Delta T=\frac{5}{2}\left(1\right)\left(8.314\right)\left(T_2-T_1\right)=2619.84\ {\rm J}\]
(d) Use the first law of thermodynamics as $\Delta U_{int}=W_{on}+Q_{in}$, where $W_{on}$ is the work done on the system and $Q_{in}$ stand for the heat transfer into the system.
\[\left(1\to 2\right):isobaric:\ \left\{ \begin{array}{c} W_{on}=-P\Delta V=-\left(1.31\times {10}^5\right)\left(24-16\right)\times {10}^3=-1048\ {\rm J} \\ Q_{in}=2619.84\ {\rm J} \end{array}\right.\]
\[\left(2\to 3\right):adiabatic\left\{ \begin{array}{c}W_{on}=C_V\Delta T=\frac{3}{2}nR\Delta T=\frac{3}{2}(1)(8.314)(491.58-378.15)=1414.65)\ {\rm J} \\ Q_{in}=0 \end{array}\right.\]
\[\left(3\to 1\right):isochoric\left\{ \begin{array}{c}W_{on}=-P\Delta V=0 \\ Q_{in}=C_V\Delta T=\frac{3}{2}\left(1\right)\left(8.314\right)\left(252.1-491.58\right)=-2986.55\ {\rm J} \end{array}\right.\]
\[\Rightarrow \ W_{tot}=W_{1\to 2}+W_{2\to 3}+W_{3\to 1}=-1048+141465+0=\ +366.35\ {\rm J}\ \ \ \]
A sample of Helium (ideal and monoatomic) is placed inside a piston. The walls of the  piston are perfectly insulating and so no heat flows in or out the gas. Initially, the pressure is $1\ {\rm atm}$ and the volume is $1.00\times {10}^{-3}\ {{\rm m}}^{{\rm 3}}$. Now the pressure of the He is doubled, to $2\ {\rm atm}$. ($1\ {\rm atm=1.013\times }{{\rm 10}}^{{\rm 5}}\ {\rm Pa}$).
piston are perfectly insulating and so no heat flows in or out the gas. Initially, the pressure is $1\ {\rm atm}$ and the volume is $1.00\times {10}^{-3}\ {{\rm m}}^{{\rm 3}}$. Now the pressure of the He is doubled, to $2\ {\rm atm}$. ($1\ {\rm atm=1.013\times }{{\rm 10}}^{{\rm 5}}\ {\rm Pa}$).
(a) What is the final volume of the Helium?
(b) The head of the piston has an area of $0.01{{\rm m}}^{{\rm 2}}$. What is the external force that must be exerted on the piston to maintain the Helium in its the compressed ($2\ {\rm atm}$) state?
(a) Because there is no heat flow in this piston that is $Q=0$ thus we have an adiabatic process. Using the equation of state for an adiabatic process i.e. $PV^\gamma=Constant$. Between initial and final states, we obtain
\[P_1V^\gamma_1=P_2V^\gamma_2\Rightarrow V_2={\left(\frac{P_1}{P_2}\right)}^{\frac{1}{\gamma}}V_1\]
\begin{align*}\therefore\ \ V_2&={\left(\frac{1}{2}\right)}^{\frac{1}{\frac{5}{3}}}\left({10}^{-3}\right)\\&=6.6\times {10}^{-4}\ {{\rm m}}^{{\rm 3}}\end{align*} Where $\gamma=\frac{C_P}{C_V}=\frac{\frac{5}{2}nR}{\frac{3}{2}nR}=\frac{5}{3}$
(b) By definition, the pressure due to an external force is $P=\frac{F}{A}$, where $A$ is the cross-sectional area of the object.
In this problem, two forces acting on the piston: external force $F$ and air pressure $P_0$. Since we want the head of the piston maintains fixed so the net force on the piston must be zero.\begin{gather*} \Sigma F_{ex}=0\Rightarrow F+P_0A=PA\Rightarrow F=\left(P-P_0\right)A\\\therefore F=\left(2-1\right)\left(1.013\times {10}^5\right)\left(0.01\right)=1.013\times {10}^3\ {\rm N}\end{gather*}
The figure shows a $50{\rm kg}$ lead cylindrical piston which floats in equilibrium on $0.89\ {\rm mol}$ of compressed air at $30{\rm{}^\circ\,\!C}$. What is the height $h$ of the piston?
$0.89\ {\rm mol}$ of compressed air at $30{\rm{}^\circ\,\!C}$. What is the height $h$ of the piston?
First, draw a free body diagram and then use the equilibrium condition that is $\Sigma F_y=0$ to find the pressure of the piston. 
\[\Sigma F_y=0\Rightarrow P_0A+mg-PA=0\]
\[\Rightarrow P=P_0+\frac{mg}{A}=P_0+\frac{mg}{\pi r^2}\]
\[P=\left(1.01\times {10}^5\right)+\frac{50\times 9.8}{\pi{\left(0.05\right)}^2}=1.633\times {10}^5\ {\rm Pa}\]
Now use the equation of state for the ideal gas confined in the piston i.e. $PV=nRT$
\[\Rightarrow V_{cylinder}=\frac{nRT}{P}=\left(\pi r^2\right)h\Rightarrow h=\frac{nRT}{P\left(\pi r^2\right)}\]
\[\Rightarrow h=\frac{\left(0.89\right)\left(8.314\right)\left(273+30\right)}{\left(1.633\times {10}^5\right)\pi{\left(0.05\right)}^2}=1.748\ {\rm m=174.8\ cm}\]
Note: in the equation of state, the temperature of the gas must be in Kelvins i.e. $T\left(K\right)=273+T({\rm{}^\circ\,\!C})$
An expansion process on an ideal diatomic gas has a linear path between the initial and final states on a $PV$ diagram. The initial pressure is $300\ {\rm kPa}$, the initial volume is $0.090\ {{\rm m}}^{{\rm 3}}$, and the initial temperature is $390{\rm K}$. The final pressure is $80\ {\rm kPa}$ and the final temperature is $300\ {\rm K}$. How much work done by the gas in this process?
First, draw its $PV$ diagram as 
The work done on the gas is defined as $W_{on}=-P\Delta V$ . The work done by the gas is the negative of the work done on the gas i.e.
\[W_{by}=-W_{on}=P\Delta V\]
Or the area under a PV diagram represents the work done by the gas. Therefore, we must calculate the area of the shaded trapezoid in the figure.
\[W_{by}=S_{under}=\frac{\left(P_2+P_1\right)\Delta V}{2}\]
Find the final volume of the gas using $\frac{P_1V_1}{T_1}=\frac{P_2V_2}{T_2}\ $
\[\Rightarrow V_2=\frac{T_2}{T_1}\frac{P_1}{P_2}V_1=\frac{300}{390}\frac{300}{80}\left(0.090\right)=0.260\ {{\rm m}}^{{\rm 3}}\]
\[W_{by}=\frac{\left(80+300\right)\times {10}^3}{2}\ \left(0.260-0.09\right)=32300\ {\rm J}\]
4.8 mol of gas #1 initially has 9000 J of thermal energy. It interacts with 3.4 mol of gas #2, which initially has 5000 J of thermal energy. If both gases are monatomic, what is the change in the thermal energy of gas #1?
The thermal energy is a form of internal energy or the amount of energy needed to increase the temperature of an object which is given by $Q=nC_VT$, $C_V$ is the heat capacity at constant volume. For monoatomic ideal gasses $C_V=\frac{3}{2}R$. Therefore, using equation above, find the initial temperature of the gas
\[Q_1=n_1C_{V1}T_1\Rightarrow T_1=\frac{9000}{\left(4.8\right)\frac{3}{2}\left(8.314\right)}=150.3\ {\rm K}\]
The temperature must be in Kelvins and $R=8.314\ {\rm J/(mol.K)}$.
After mixing the two gasses the combined gas has the thermal energy
\[Q_f=Q_1+Q_2=9000+5000=14000\ {\rm J}\]
Now compute the final temperature of the system as
\[T_f=\frac{Q_f}{\left(n_1+n_2\right)C_V}=\frac{14000}{\left(4.8+3.4\right)\frac{3}{2}(8.314)}=136.9\ {\rm K}\]
Thus, the change in the thermal energy of the gas $\#1$ is
\begin{align*}\Delta Q_1&=n_1C_V\left(T_f-T_1\right)\\ &=\left(4.8\right)\left(\frac{3}{2}\right)\left(8.314\right)\left(136.9-150.3\right)\\&=-802.1\ {\rm J}\end{align*} The negative indicates that the heat is transferred out of the gas $\#1$.
2 moles of Helium (monoatomic) at an initial temperature of 300 K come into contact with 4 moles of Oxygen (diatomic) at an initial temperature of 600 K. What is the final temperature?
Note: In a monoatomic molecule, there are three degrees of freedom (DOF) due to the translational motion.
In a diatomic molecule, in addition to translational symmetry, we have two extra degrees of freedom due to the rotational symmetry, and the two DOF for vibrational symmetry. Therefore, in a diatomic molecule, we have 7 degrees of freedom (DOF).
Equipartition of energy states that each of the DOF contributes $\frac{1}{2}kT$ per molecule (or $\frac{1}{2}RT$ per mol) to the internal energy of the system. Thus ${\left(E_{int}\right)}_{di}=\frac{7}{2}kT$ but in moderate temperatures that the molecule do not vibrate, the internal energy of a diatomic gas is defined by ${\left(E_{int}\right)}_{di}=\frac{5}{2}kT$.
The total internal energy of the combined gas is the sum of each of the internal energies
\begin{align*} {\left(E_{int}\right)}_{tot}&={(E_{int})}_{mono}+{\left(E_{int}\right)}_{di} \\\\ &=\frac{3}{2}n_1RT_1+\frac{5}{2}n_2RT_2 \\\\ {\left(E_{int}\right)}_{tot}&=\left[\frac{3}{2}(2)(300)+\frac{5}{2}(4)(600)\right]\left(8.314\right) \\\\&=5.74\times {10}^4\, {\rm J}\end{align*} Now use the definition of the internal energy to find the final temperature as \begin{gather*} {\left(E_{int}\right)}_{tot}=C_VT_f=\left(\frac{3}{2}n_{He}R+\frac{5}{2}n_{O_2}R\right)T_f\\ \Rightarrow 5.74\times {10}^4=\left(\frac{3}{2}(2)+\frac{5}{2}(4)\right)(8.314)T_f\\ \\ \Rightarrow \quad \boxed{T_f=531\,\rm K}\end{gather*}
The graph in the figure shows a cycle for a heat engine for which $Q_H=50\ {\rm J}$. What is the thermal efficiency of this engine?
is the thermal efficiency of this engine?
The thermal efficiency of a heat engine is defined as the ratio of the magnitude of the work done by the engine to the magnitude of the heat absorbed from the high-temperature reservoir
\[e=\frac{\left|W\right|}{\left|Q_H\right|}\]
Recall that the area under a PV diagram represents the work done by the gas so
\begin{align*} W_{by}&=S_{triangle}\\ &=\frac{1}{2}\left(200\times {10}^{-6}-100\times {10}^{-6}\right)\left(400\times {10}^3-200\times {10}^3\right)\\ &=10\ {\rm J} \end{align*}
So $e=\frac{\left|W\right|}{\left|Q_H\right|}=\frac{10}{50}=0.2=20\%$
An ideal monoatomic ideal gas cools from $455\,{\rm K}$ to $405\,{\rm K}$ at constant volume as $831\ {\rm J}$ of energy is removed from it. How many moles of gas are in the sample?
The amount of heat that a system absorbs or release at a constant volume is determined by
\[Q=nC_V\Delta T\xrightarrow{mono}\ Q=\frac{3}{2}nR\Delta T\]
Where $C_V$is the heat capacity at constant volume and $n$ is the number of moles. So
\[n=\frac{2Q}{3R\Delta T}=\frac{2\times (-831)}{3\times 8.314\times \left(405-455\right)}=1.33\ {\rm mole}\]
Note: the minus sign is due to the heat removed (the gas is cooled) from the sample!
Assuming the radius of diatomic molecules is approximately $1.0\times {10}^{-10}{\rm m}$, for what pressure will the mean free path in room-temperature ($20{\rm{}^\circ\,\!C}$) nitrogen be $4.6{\rm m}$?
The mean free path $\lambda$ of a molecule with diameter $d$ and number of molecules per unit volume $n_V$ is determined by $\lambda=1/\sqrt{2}\left(n_V\pi d^2\right)$. First find the $n_V$ then use the $PV=Nk_BT$ to find the desired pressure.
\[\lambda=\frac{1}{\sqrt{2}\left(n_V\pi d^2\right)}=\frac{1}{\sqrt{2}\left(\frac{N}{V}\right)\pi{\left(2r\right)}^2}\Rightarrow n_V=\frac{N}{V}=\frac{1}{4\sqrt{2}\pi r^2\lambda}\]
\[\left\{ \begin{array}{c} \frac{N}{V}=\frac{1}{4\sqrt{2}\pi r^2\lambda} \\ P=\frac{N}{V}k_BT \end{array}\right.\]
\begin{align*}\Rightarrow P&=\frac{1}{4\sqrt{2}\pi r^2\lambda}k_BT\\&=\frac{\left(1.381\times {10}^{-23}\right)\left(273+20\right)}{4\sqrt{2}\pi{\left({10}^{-10}\right)}^2\left(4.6\right)}\\&=4.95\times {10}^{-3}{\rm Pa}\end{align*}
\[or\ \ 4.95\times {10}^{-3}{\rm Pa}\frac{{\rm 1\ atm}}{{\rm 1.01\times }{{\rm 10}}^{{\rm 5}}{\rm Pa}}{\rm =4.9\times }{{\rm 10}}^{{\rm -}{\rm 8}}\ {\rm atm}\]
A sample of an ideal gas is slowly compressed to one-half its original volume with no change in temperature. What happens to the root-mean-square of the molecules in the sample?
The rms of a molecule of a gas is dependent only on the absolute temperature of the gas and is found by the following relation
\[v_{rms}=\sqrt{\frac{3k_BT}{m}}=\sqrt{\frac{3RT}{M}}\]
Where $M$ is the molar mass of the sample. Since this process is isothermal, the temperature of the gas does not change, so $v_{rms}$ stays the same as the initial speed.
A perfect Carnot engine operates between the temperatures of 300 K and 700 K, drawing 60 kJ of heat from the 700 K reservoir in each cycle. How much heat is dumped into the 300 K reservoir in each cycle?
First, draw a schematic representation of a heat engine as below.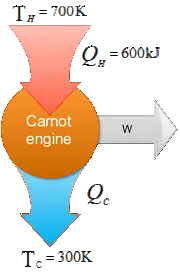
The engine absorbs heat $Q_H$ from the hot reservoir at $T_H$, does work $W$, and releases heat $Q_c$ to the cold reservoir at $T_c$.
Note: the efficiency of the Carnot cycle is defined as
\[e_{Carnot}=1-\frac{Q_c}{Q_H}=1-\frac{T_c}{T_H}\]
Therefore, first calculate the Carnot efficiency of the system then use $e=1-\frac{Q_c}{Q_H}$ to find the heat releases to the cold reservoir $Q_C$.
\begin{gather*} e=1-\frac{T_c}{T_H}=1-\frac{300}{700}=0.571\\ \frac{Q_c}{Q_H}=1-e\Rightarrow Q_c=Q_H\left(1-e\right)\\ \therefore\ \ Q_c=\left(60\times {10}^3\right)\left(1-0.571\right)=25.71\ {\rm J} \end{gather*}
A Carnot refrigerator removes heat from the freezer at $-10{\rm{}^\circ\,\!C}$ and expels it into the room at $20{\rm{}^\circ\,\!C}$. You put a tray with $0.5\ {\rm kg}$ of water at $30{\rm{}^\circ\,\!C}$ into the freezer. ($c_{ice}=2.01\times {10}^3\frac{{\rm J}}{{\rm K.kg}}$, $c_w=4190\frac{{\rm J}}{{\rm K.kg}}$, $L_f=334\times {10}^3\frac{{\rm J}}{{\rm K}}$)
(a) Calculate the performance coefficient of this refrigerator.
(b) Calculate the heat energy extracted from this water when it is cooled and transformed to ice at $-10{\rm{}^\circ\,\!C}$.
(c) Calculate the work done by the compressor of the refrigerator in order to achieve this transformation (of part (b)).
(d) Calculate the heat that the refrigerator expels into the room while achieving this transformation.
(a) A refrigerator is a heat engine run backward that is its engine absorbs heat from the cold reservoir (interior medium) and releases heat to the hot reservoir (surrounding). For any refrigerator, there is a number called Coefficient of Performance (COP) as the ratio of the magnitudes of heat absorbed from the cold reservoir to the work done on the refrigerator i.e. ${\rm COP}={\left|Q\right|}_c/\left|W\right|$. Another version of the COP is, by using the conservation of energy, ${\rm COP}=T_c/(T_H-T_c)$. Therefore, first convert all temperatures into the Kelvins then substitute in above equation
\begin{gather*} T_H\left({\rm K}\right)=273+T\left({\rm{}^\circ\,\!C}\right)=273+20=293\ {\rm K}\\T_c\left({\rm K}\right)=273+T\left({\rm{}^\circ\,\!C}\right)=273-10=263\ {\rm K}\\\Rightarrow {\rm COP=}\frac{293}{293-263}=8.77\end{gather*}
(b) All of the processes are as follows
\[Water\ 30{\rm{}^\circ\,\!C}\xrightarrow{Q_1}water\ 0{\rm{}^\circ\,\!C}\xrightarrow{Q_2}ice\ 0{\rm{}^\circ\,\!C}\xrightarrow{Q_3}ice-10{\rm{}^\circ\,\!C}\]
Now calculate the heats
\begin{gather*} Q_{lost}=\underbrace{m_wc_c\left(0-30{\rm{}^\circ\,\!C}\right)}_{Q_1}+\underbrace{m_wL_f}_{Q_2}+\underbrace{m_wc_{ice}\left(-10{\rm{}^\circ\,\!C}-0\right)}_{Q_3}\\=0.5\times 4190\left(-30\right)+0.5\times \left(-334\times {10}^3\right)+0.5\times \left(2.01\times {10}^3\right)\left(-10\right)=-239900{\rm J} \end{gather*}
Note: freezing of the water is a reverse process of melting of the ice so $Q=-mL_f$.
(c)Use the definition of the COP and find the work done by the refrigerator's engine
\[COP=\frac{\left|Q_c\right|}{\left|W\right|}\Rightarrow W=\frac{239900}{8.77}=27400\ {\rm J}\ \]
(d) During a refrigeration process energy is conserved so using the conservation of energy, we obtain
\begin{gather*} \left|W\right|+\left|Q_c\right|=\left|Q_H\right|\\ \Rightarrow \left|Q_H\right|=27400+239900=267000\ {\rm J} \end{gather*}
An ideal gas initially at 300 K and occupying a volume of 20 L is adiabatically compressed. If its final temperature is 400 K and $\gamma=1.5$, what is its final volume?
Since this process is adiabatic, so its equation of state is
$PV^\gamma=Constant$ or $TV^{\gamma-1}=Constant$. Therefore, use the second equation between points 1 and 2.
\begin{gather*} T_1V^{\gamma-1}_1=T_2V^{\gamma-1}_2\\\Rightarrow {\left(\frac{V_2}{V_1}\right)}^{\gamma-1}=\frac{T_1}{T_2}\\ \Rightarrow V_2={\left(\frac{T_1}{T_2}\right)}^{\frac{1}{\gamma-1}}V_1={\left(\frac{300}{400}\right)}^{\frac{1}{1.5-1}}\left(20\right)\\ =11.25\ {\rm Lit} \end{gather*}
Note: $\gamma$ is the ratio of the heat capacities at constant pressure and volume i.e. $\gamma=C_P/C_V$, which is a dimensionless quantity.
In the PV diagram on the right, 120 J of work was done by 0.12 mol of ideal gas during the adiabatic process $a\to b$. ($1\,{\rm atm}=1.013\times 10^5\,{\rm Pa}$ and $1\,{\rm L}=10^{-3}\,{\rm m^3}$)
(a) How much heat entered or left this gas from $a$ to $b$?
(b) By how much did the internal energy change?
(c) What is the temperature of the gas at $b$?
(a) In adiabatic process, the heat exchange is always zero. So $Q=0$
(b) Using the first law of thermodynamics (energy conservation), we get
\[\Delta U_{int}={{\rm Q}}_{{\rm in}}+W_{on}\]
Where $W_{on}$ is the work done on the system. By convention, the negative of the work done on the system equals the work done by the system. Therefore,
\[\Delta U_{int}=0+W_{on}=-120\ {\rm J}\]
(c) Apply the ideal gas law at point $b$ as follows
\[PV=nRT\ \]
\[\Rightarrow T_b=\frac{P_bV_b}{nR}=\frac{\left(6\times {10}^{-3}\right)\left(1\times 1.013\times {10}^5\right)}{\left(0.12\right)\left(8.314\right)}=609\ {\rm K}\]
A metal rod has a thermal expansion coefficient of $6.44\times {10}^{-5}\ {{\rm{}^\circ\,\!C}}^{-1}$. Initially, the rod has a temperature of $55.6{}^\circ\, {\rm F}$ at some initial length. The rod is heated to $412\,{\rm {}^\circ\, F}$ which causes it length to change by $3.89\ {\rm mm}$. What must have been the initial length of the rod in ${\rm cm}$?
The change in length for a given change in temperature is $\Delta L=L_0a\Delta T$ where $a$ is the coefficient of linear expansion and $T$ is absolute temperature (must be in Kelvins).
In this problem, the temperature has given in Fahrenheit so first must be converted to Celsius as $T\left({}^\circ\, F\right)=\frac{9}{5}T\left({\rm{}^\circ\,\!C}\right)+32$. Since an $1\ {\rm K}$ increase in temperature equals a $1{\rm{}^\circ\,\!C}$ that is $\Delta T_c=\Delta T_K$ use this note to convert the change in Fahrenheit to the change in Celsius as
$\Delta T_c=\frac{5}{9}{\Delta T}_F=\frac{5}{9}(412-55.6)=198{\rm{}^\circ\,\!C}$ since $\Delta T_c=\Delta T_K$ we have $\Delta L=L_0a\Delta T$
\begin{align*} \Rightarrow \ \ L_0&=\frac{\Delta L}{a\Delta T}\\&=\frac{3.89\ {\rm mm}}{\left({\rm 6.44\times }{{\rm 10}}^{{\rm -}{\rm 5}}\right)\left(198\right)}\\&={\rm 305\ mm\times }\left(\frac{{\rm 1cm}}{{\rm 10mm}}\right)\\&={\rm 30.5\ cm}\end{align*}
A metal rod that is 92.2 cm long at $22.2^\circ C$ is observed to be 94.6 cm long at $96.6^\circ C$. What is the coefficient of linear expansion of this metal?
By definition, the coefficient of linear expansion is $a=\Delta L/L_0\Delta T\ $so
\begin{align*} a&=\frac{L-L_0}{L_0\left(T-T_0\right)}\\\\&=\frac{94.6-92.2}{\left(92.2\right)\left(96.6-22.2\right)}\\\\&=3.50\times {10}^{-4}\,^\circ C\end{align*}
The ends of a cylindrical steel rod (with length $L$ and radius $R$) are maintained at two different temperatures. The rod conducts heat from one end to the other at a rate of $20\ {\rm cal/s}$. At what rate would a steel rod (with length 2 and radius 2R) conduct heat between the same two temperatures?
One of the methods of heat transfer is conduction. Let us consider a slab with length $L$ and cross-sectional area $A$ which is located at different temperatures $T_H$ and $T_C$. The rate of heat transfer is computed by the following equation
\[\frac{Q}{t}=kA\frac{T_H-T_C}{L}\]
The given data are $A_2=\pi{\left(2R\right)}^2=4\pi R^2=4A_1\ ,\ \ L_2=2L_1$ so using the conduction equation, we obtain
\[\frac{Q_2}{t}=k\frac{A_2\Delta T}{L_2}=k\frac{4A_1\Delta T}{2L_1}\ \]
\[\Longrightarrow \frac{Q_2}{t}=2\ kA_1\frac{\Delta T}{L_1}=2\frac{Q_1}{t}=2\times 20=40\ {\rm cal/s}\]
Suppose that the insulating qualities of the wall of a house come mainly from a $0.100\ {\rm m}$ layer of brick with thermal conductivity $k_B=10.0\, {\rm J/(s.m.}{\rm{}^\circ\,\!C}{\rm )}$ and a $0.400\, {\rm m}$ layer of insulation with thermal conductivity $k_I=9.00\times {{\rm 10}}^{{\rm -}{\rm 2}}{\rm \ J/(s.m.}{\rm{}^\circ\,\!C}{\rm )}$. The temperature on the side of the brick is $T_B=10.0\,{\rm{}^\circ\,\!C}$ while the temperature on the side of the insulating material is $T_I=30.0{\rm{}^\circ\,\!C}$.
(a) What is the temperature at the interface brick/insulator? 
(b) What is the total rate of heat loss$\ Q/t$ through such a wall, if the total area is $10.0\ {{\rm m}}^{{\rm 2}}$?
(c) A copper water pipe of length $1.00\ {\rm m}$ is moved from inside the house (at ${\rm 30.0}{\rm{}^\circ\,\!C}$) to the outside of the house (at $10.0\ {\rm{}^\circ\,\!C}$). What is the change in the length of this pipe after it adapts to the temperature? The coefficient of thermal linear expansion for copper is $\alpha=\ 1.70\times {10}^{-5}{\left({\rm{}^\circ\,\!C}\right)}^{-1}$ .
(a) The thermal current $dQ/dt$ is the same at the interface so use the following relation for the thermal current through a substance with thermal conductivity $k$
 \begin{gather*}I=\frac{dQ}{dt}=-kA\frac{\Delta T}{\Delta x}\\ {\rm where}\ \Delta T=T_{cooler}-T_{warmer}\end{gather*}
\begin{gather*}I=\frac{dQ}{dt}=-kA\frac{\Delta T}{\Delta x}\\ {\rm where}\ \Delta T=T_{cooler}-T_{warmer}\end{gather*}
Since $I_{B\to I}=I_{I\to B}$ therefore
\begin{gather*} k_B\frac{A\left(T-T_B\right)}{L_B}=K_I\frac{A\left(T_I-T\right)}{L_I}\\\Rightarrow T=\frac{\frac{k_IT_I}{L_B}+\frac{k_BT_B}{L_B}}{\frac{k_B}{L_B}+\frac{k_I}{L_I}}=10.04{\rm{}^\circ\,\!C}\end{gather*}
(b) Since the inner and outer temperature is constant, so no heat accumulated in the wall. Therefore, the heat conducted through the brick must equal to the insulation, that is ${\left(\frac{Q}{t}\right)}_B={\left(\frac{Q}{t}\right)}_I$. Choosing ${\left(\frac{Q}{t}\right)}_I$, we have
\begin{align*} {\left(\frac{Q}{t}\right)}_I&=-k_I\frac{A\left({T-30}{\rm{}^\circ\,\!C}\right)}{l_{I}}\\&=-9\times {10}^{-2}\frac{\left(10\right)\left(10.04{\rm{}^\circ\,\!C}-30{\rm{}^\circ\,\!C}\right)}{0.4}\\&=44.91\ {\rm J}\end{align*}
(c) When we have a temperature drop $\Delta T$ across a length $L_0$, due to the thermal expansion, the change in the length is given by $\Delta L=L_0a\Delta T$. Therefore,
\[\Delta L=\left(1\right)\left(1.7\times {10}^{-5}\right)\left(30-10\right)=3.4\times {10}^{-4}\ {\rm m}\]
A glass windowpane is 1.7 m high, 1.4 m wide, and 2 mm thick. The temperature at the inner surface of the glass is $16{\rm{}^\circ\,\!C}$ and at the outer surface $4{\rm{}^\circ\,\!C}$. How much heat is lost each hour through the window under steady-state conditions?
The heat $Q$ conducted through a bar of length $L$ and cross sectional area $A$  during a time $t$ is given by the
during a time $t$ is given by the
\[Q=k\frac{A\Delta T}{L}t\]
where $k$ is the thermal conductivity of the material and $\Delta T=T_H-T_C$.\begin{align*} Q&=k\frac{A\left(T_H-T_C\right)}{L}t\\ \\&=\left(0.8\right)\frac{\left(1.7\times 1.4\right)\left(16-4\right)}{0.002}\left(60\times 60\right)\\ \\&=4.112\times {10}^7\ {\rm J} \end{align*}
What is the net power that a person loses through radiation if her surface area is $1.2\,{\rm m^2}$, if her emissivity is 0.895, if her skin temperature is 300 K and if she is in a room that is at a temperature of $17^\circ C$?
Note: the net power radiated by an object with surface area $A$ at temperature $T$ to its environment at $T_0$ is determined by the Stefan-Boltzmann law as $P_{net}=e\sigma A(T^4-T^4_0)$ where $e$ is the emissivity of the object and $\sigma$ is Stefan-Boltzmann constant. Therefore,
\[P_{net}=\left(0.895\right)\left(1.2\right)\left(5.6703\times {10}^{-8}\right)\left({300}^4-{290}^4\right)=62.55{\rm W}\]
Note: $T$ must be in Kelvins. ($T\left(K\right)=273+17{\rm{}^\circ\,\!C}=290{\rm K}$)
A woman's body has a surface area of $1.4\,{\rm m^2}$ and her skin temperature is $\rm 27^\circ C$. Her surroundings have a temperature of $\rm 17^\circ C$. (recall that the emissivity can be taken to be 1 for human skin)
(a) Calculate the rate at which she emits heat radiation.
(b) Calculate the rate at which she absorbs heat radiation from the surroundings.
(c) What is the net rate at which she emits heat?
(a) The power radiated by an object with surface area $A$ at absolute temperature $T$ is given by
\[P=Ae\sigma T^4\]
Where $e$ is emissivity and $\sigma$ is the Stefan- Boltzmann constant.
Therefore, we must first find the absolute temperatures of skin and surroundings
\begin{align*} T_{skin}&=273+T(\rm ^\circ C) \\ &=273+27=300\quad \rm K \\\\ P_{emit}&=Ae\sigma T^4 \\&=1.4\times 1\times (5.67\times {10}^{-8}) \times (300)^4 \\ &=643\quad \rm W \end{align*}
(b) Same as the previous part
\begin{align*}T_{surr}&=273+T(\rm ^\circ C) \\&=273+17=290\quad \rm K \\\\ P_{surr}&=AesT^4\\ &=1.4\times 1\times (5.67\times {10}^{-8})\times (290)^4 \\ &=562\quad \rm W \end{align*}
(c) The net power radiated is the difference of them as follows
\begin{align*} P_{net}&=P_{skin}-P_{surr} \\ &=643-562 \\& =81\quad \rm W \end{align*}
A 30000 kg subway train is initially at $20\ {\rm m/s}$. it slows to a stop at a station and stays there long enough for the brakes to cool. All the kinetic energy lost by the train is released as heat into the station, which is $10\ {\rm m}$ high, 20 m wide, and 50 m long. Air has density of $1.2\,{\rm kg/m^3}$ and a heat capacity of $1020\, {\rm J/(kg.K)}$.
(a) Calculate the mass of the air.
(b) Calculate the heat absorbed by the air.
(c) Calculate the change in the temperature of the air due to absorption of this heat.
(a) By definition, mass is equals to the density times the volume.
\[m=\rho V=1.2\times \left(10\times 20\times 50\right)=12000\ {\rm kg}\]
(b) All of the kinetic energy of the train is converted to the heat and is absorbed by the air so
\begin{gather*} K=\frac{1}{2}mv^2=Q\\\Rightarrow Q=K=\frac{1}{2}\left(30000\right){\left(20\right)}^2=6\times {10}^6\ {\rm J} \end{gather*}
(c) Use the equation $Q=mc\Delta T$ to find the change in the temperature due to the heat absorbed by the air.
\[\Delta T=\frac{Q}{m_{air}c}=\frac{6\times {10}^6}{\left(12000\right)\left(1020\right)}=0.49\ {\rm K}\]
Note: since the temperature increment of $1\ {\rm{}^\circ\,\!C}$ is the same as an increment of $1{\rm K}$ so the temperature increase of the air is equal to $0.49\ {\rm{}^\circ\,\!C}$.
The mechanical equivalent of heat is $\rm{1\, cal=4.18\, J}$. The specific heat of water is $\mathrm{1\, cal/g.K}$, and its mass density is $1\,{\rm g/cm^3}$. An electric immersion water heater, rated at $400\,{\rm W}$, should heat a liter of water from ${\rm 10^\circ C}$ to ${\rm 30^\circ C}$ in about:
(a) $12\, \rm s$
(b) $50\, \rm s$
(c) $3.5\, \rm {min}$
(d) $15\, \rm {min}$
(e) $45\, \rm {min}$
In this question, there is a change in the phase of water, so we must use the well-known formula $Q=mc\Delta T$, as we learned on the specific heat practice problems page. First, find the heat required to change the temperature of the water from ${\rm 10^\circ C}$ to ${\rm 30^\circ C}$ and then using the definition of the power determine the time required as follows
Since there is no change in the phase of water and only its temperature is changed so the heat required is calculated as $Q=mc\mathrm{\Delta }T$, where $c$ is the specific heat of the matter. Thus \begin{align*}Q&={\rm (1000 \,g)\left(1\,\frac{cal}{g.K}\right)(30-10)} \\ &={\rm 20\times 10^3 \, cal} \\ &={\rm 20\quad kcal} \end{align*}
Note: the temperature difference of one Kelvin exactly coincides with one Celsius degree.
Power is defined as the ratio of energy to time. In the definition of power, all quantities must be in SI units so we must convert cal to Joules as \begin{gather*} 20000\ \rm{cal\times 4.18\ J=83600\ J} \\\\ P=\frac{Q}{t}\Rightarrow t=\frac{Q}{P}=\frac{83600}{400}=209\rm{s=3.48\ min} \end{gather*}
The correct answer is C.
Most useful formula in Heat:
Relation between Fahrenheit and centigrade:
\[T_C=\frac{5}{9}(T_F-32\,^{\circ}\mathrm{C} )\]
Relation between Kelvins and Celsius:
\[T_K=T_C+273.15\]
Ideal gas law: $PV=nRT$
Ideal gas law between two states with fixed amount of gas:
\[ \frac{P_1V_1}{T_1}=\frac{P_2V_2}{T_2}\]
rms speed of molecules:
\[v_{rms}=\sqrt{\frac{3kT}{m}}=\sqrt{\frac{3RT}{M}}\]
$m$ is the mass of the molecules and $M$ is the molar mass.
Mean free path $\lambda$:
\[\lambda=\frac{1}{\sqrt{2}n_V\pi d^2}\]
$d$= molecule’s diameter, $n_V$= number of molecules per unit volume
Heat capacities:
\[C_V=\frac{3}{2}R \ \ (monatomic \ gas)\]
\[C_V=\frac{5}{2}R \ \ (diatomic \ gas)\]
Relation between $C_V$ and $C_P$:
\[C_P=C_V+R\]
Thermal expansion:
\[\Delta L=\alpha L_0 \Delta T\]
\[\Delta V=\beta V_0 \Delta V\]
Required heat to a temperature change $\Delta T$, without phase change
\[Q=mc\Delta T\]
Required heat to change in phase of a matter:
\[Q=\pm mL\]
$L$ is the heat of fusion $L_f$, vaporization $L_V$
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
