Solved Problems
Let $\vec{A}=2\hat{x}-2\hat{y}$ and $\vec{B}=2\hat{x}+2\hat{y}$. What is the value of the angle that lies between these two vectors?
Solution: Recall that the angle between two vectors $\vec{A}$ and $\vec{B}$ is determined by the following relation\[{\cos \theta \ }=\frac{\vec{A}.\vec{B}}{\left|A\right|\left|B\right|}\]
Where dot denotes the scalar product and $\left|\cdots \right|$ is the magnitude of the vector. Therefore, we have \begin{align*}\cos \theta &=\frac{\left(2\hat{x}-2\hat{y}\right).\left(2\hat{x}+2\hat{y}\right)}{\sqrt{2^2+{\left(-2\right)}^2}\sqrt{2^2+2^2}}\\&=\frac{4-4}{denominator}\\&=0\Rightarrow \theta =90{}^\circ \end{align*}
If two vectors are given as $\vec{A}=-12\,\rm\hat i+8\,\rm\hat j$ and $\vec{B}=24\,\rm\hat i+18\,\rm\hat j$, determine the resultant vector $\vec{R}=2\vec{A}-\frac{1}{3}\vec{B}$, and also find its magnitude ($R\ or\ \left|R\right|$) and direction (angle $\theta $ between vector and horizontal line)
Solution: The calculation of the resultant vector $R$ is straightforward as follows
\begin{align*} \vec{R}&=2\left(-12\,\rm\hat i+8\,\rm\hat j\right)-\frac{1}{3}\left(24\,\rm\hat i+18\,\rm\hat j\right)\\&=-24\,\rm\hat i+16\,\rm\hat j-8\,\rm\hat i-6\,\rm\hat j\end{align*}
\[\therefore \ \ \vec{R}=-32\,\rm\hat i+10\,\rm\hat j\]
The magnitude of vector $\vec{A}$ with vector components $A_x$ and $A_y$ is given by \[\left|\vec{A}\right|=\sqrt{A^2_x+A^2_y}\] And its direction with respect to the horizontal line is \[\theta ={{\tan}^{-1} \left(\left|\frac{A_y}{A_x}\right|\right)\ }\]
Therefore, the magnitude and direction of the resultant vector $\vec{R}$ is
\begin{align*}\left|\vec{R}\right|&=\sqrt{{\left(-32\right)}^2+{\left(10\right)}^2}\\&=33.5\mathrm{m}\\ {\theta }_R&={{\tan}^{-1} \left(\left|\frac{10}{-32}\right|\right)\ }\\&=17.4{}^\circ \end{align*}
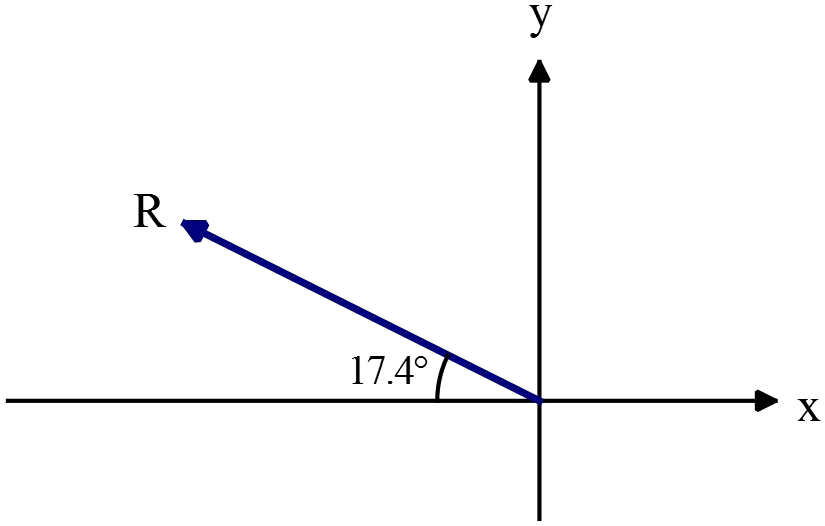
Since $A_y>0$ and $A_x<0$ so the resultant vector $\vec{R}$ lies in the second quadrant of the coordinate system.
Thus $\vec{R}=(33.5\ \mathrm{m,\ 17.4{}^\circ \ north\ of\ west)}$ is shown in the figure below.
Find the angle between the two vectors $\vec{F}=\left(3\,\rm\hat i-4\,\rm\hat j+5\hat{k}\right)\mathrm{N}$ and $\vec{s}=\left(2\,\rm\hat i-3\hat{k}\right)\mathrm{\ N}$.
The angle between two vectors is given by the following relation
\begin{align*}
{\cos \theta \ }&=\frac{\vec{A}.\vec{B}}{\left|A\right|\left|B\right|}\\
&=\frac{\left(3\,\rm\hat i-4\,\rm\hat j+5\hat{k}\right).\left(2\,\rm\hat i-3\hat{k}\right)}{\sqrt{3^2+{\left(-4\right)}^2+5^2}\sqrt{2^2+{\left(-3\right)}^2}}\\
&=\frac{3\times 2+5\times \left(-3\right)}{\sqrt{50}\sqrt{13}}\\
&=110.67{}^\circ
\end{align*}
$\vec{A}.\vec{B}$ is scalar product which is defined as
\begin{align*}
A.B &=\left(A_x\,\rm\hat i+A_y\,\rm\hat j+A_z\hat{k}\right).\left(B_x\,\rm\hat i+B_y\,\rm\hat j+B_z\hat{k}\right)\\
& =A_xB_x\left(\underbrace{\rm\hat i.\rm\hat i}_{1}\right)+A_xB_y\left(\underbrace{\rm\hat i.\,\rm\hat j}_{0}\right)+A_zB_x\left(\underbrace{\hat{k}.\rm\hat i}_{0}\right)+\dots\\
&=A_xB_x+A_yB_y+A_zB_z
\end{align*}
$\left|\vec{A}\right|$ and $\left|\vec{B}\right|$ are the magnitudes of the corresponding vectors $\vec{A}$ and $\vec{B}$ which are defined as
\[\left|\vec{A}\right|=\sqrt{A^2_x+A^2_y+A^2_z}\]
