AP Physics 1: Circular Motion and Gravitation Practice Problems +Answers

Over 20 multiple-choice questions on circular motion and gravitation, featured in the AP Physics 1 exam, are provided with detailed explanations.

AP Physics: Circular Motion Solved Problems

Problem (1): A motorcycle weighing $200\,{\rm kg}$ turning around an unbanked circular track of radius $12.5\,{\rm m}$ at a constant speed of $56\,{\rm km/h}$. What is the magnitude of the net force applied on the motorcycle?

(a) $3.844\times 10^{3}\,\rm N$ (b) $5.0176\times 10^{4}\,\rm N$
(c) $248\rm N$ (d) $3.844\times 10^{4}\,\rm N$

Solution: Because the motorcycle moves around a circular path at a constant speed $v$, it experiences a centripetal force, which is given by the formula: \[F_c=m\frac{v^2}{r}\] Plugging the numerical values into the formula, we get: \[F_c=200\times \frac{(15.5)^2}{12.5}=3844\,{\rm N}\] Usually, the constant speed is given in units of $\rm \frac{km}{h}$. To use the centripetal acceleration or force formula, we must convert the speed into SI units ($\rm \frac ms$) by multiplying by $\frac{10}{36}$. Thus, the given speed in SI units is: \[56\times \frac{10}{36}=15.5\,{\rm m/s}\] Thus, the correct answer is (a).

Problem (2): A $355-\rm g$ ball is fastened at the end of a $1.1-\rm m$ long rope and is whirled in a vertical circle at a constant speed of $3.75\,\rm m/s$. The tensions in the rope when the ball is at the top and the bottom of its path are, respectively, closest to

(a) $2\, ,\, 7$ (b) $8\, ,\, 1$
(c) $1\, ,\, 8$ (d) $1\, ,\, 9$

Solution: The free-body diagram below shows the forces exerted on the ball at the top and the bottom of the path. In both positions, the weight force is always directed downward, but the tension is downward at the top and upward at the bottom. Meanwhile, the centripetal force is always directed toward the center of the circle at each position.

Applying Newton's second law, we have: \begin{gather*} F_c=T+mg \quad \text{top} \\\\ \frac{mv^2}{r}=T+mg \\\\ \Rightarrow T=\frac{0.355\times (3.75)^2}{1.1}-(0.355)(9.8)\\\\ \Rightarrow \boxed{T=1.06\,\rm N} \\\\ F_c=T-mg \quad \text{Bottom}\\\\ \frac{mv^2}{r}=T-mg \\\\ \Rightarrow T=\frac{0.355\times (3.75)^2}{1.1}+(0.355)(9.8) \\\\ \Rightarrow \boxed{T=8.02\,\rm N}\end{gather*} Hence, the correct answer is (c).

Problem (3): A small bead of mass $20\,\rm g$ is attached to the end of light string $120\,\rm cm$-long and is deflected at an angle of $18\circ$. Once the bead is released, what is the speed of the bead in $\rm m/s$?

(a) $1.3$ (b) $3.2$
(c) $0.55$ (d) $3.5$

Solution: When the bead is held in your hand at an arbitrary angle, say $18\deg$, the tension in the string is given by $T\cos\theta=mg$, as shown in the free-body diagram below. After releasing the bead, it moves around a semi-circle under the string's tension. As a consequence, it experiences a centripetal force whose magnitude is: \[T=F_c=\frac{mv^2}{\ell}\] where $\ell$ is the string's length. Substituting the expression for tension from the first equation, $T=\frac{mg}{\cos\theta}$, into the second one and solving for the speed $v$: \begin{align*} \frac{mg}{\cos\theta}&=\frac{mv^2}{\ell}\\\\ \Rightarrow v&=\sqrt{\frac{g\ell}{\cos\theta}}\\\\&=\sqrt{\frac{1.2\times 9.8}{\cos 18^\circ}}\\\\&=3.5\quad\rm m/s\end{align*} Thus, the correct answer is (d).

Problem (4): In a horizontal circle of radius $85\,{\rm cm}$, a constant force of $245\,\rm N$ is applied to a $2.5\,\rm kg$ object as it revolves around the track. The speed of the object (in $\rm m/s$) is closest to

(a) $91.3$ (b) $9.13$
(c) $83.3$ (d) $8330$

Solution: All information required to use the centripetal force formula $F_c=\frac{mv^2}{r}$ is given except the object's speed, $v$. Rearranging the formula to solve for $v$ and substituting the known values, we get: \begin{align*} v&=\sqrt{\frac{rF_c}{m}}\\\\ &= \sqrt{\frac{0.85\times 245}{2.5}}\\\\&=\boxed{9.13\quad \rm m/s}\end{align*} Thus, the correct choice is (b).

Problem (5): At the end of a very light string $2-\rm m$-long, a $500-\rm g$ toy is attached and whirled around a circle on a frictionless surface. Assume the maximum tension that the string can withstand is $350\,\rm N$ without breaking. What is the maximum speed the toy can have in $\rm m/s$ in this situation?

(a) $26$ (b) $37$
(c) $19$ (d) $42$

Solution: The toy whirled around a circular, frictionless path, experiencing an inward centripetal force, provided by the tension in the string. The magnitude of this centripetal force, which equals the tension, is given by: $T=F_c=\frac{mv^2}{r}$. Substituting the numerical values into the above formula and solving for $v$, we have \begin{align*} v^2&=\frac{rT}{m}\\\\&=\frac{2\times 350}{0.5}\\\\&=\sqrt{1400}\\\\ \Rightarrow v&=37.5\quad\rm m/s\end{align*} which is closest to (b).

Problem (6): A race road is designed with a curve of radius $100\,\rm m$ and banked at an angle of $45^\circ$. What maximum speed a race car can have on this road without friction in $\rm m/s$?

(a) $25$ (b) $36$
(c) $31$ (c) $69$

Solution:

Problem (7): A $1000-\rm kg$ motorcycle is moving at a constant speed of $30\,\rm m/s$ around a horizontal unbanked curve whose radius is $100\,\rm m$. To keep the car from sliding, how much friction force is required in $\rm N$?

(a) $9000$ (b) $8000$
(c) $7500$ (d) $6000$

Solution: The motorcycle wants to turn around a circular path, so a centripetal force toward the center of the circle is applied to it. This force, provided by friction, is given by: $F_c=\frac{mv^2}{r}$. Without friction, the motorcycle would slide and deviate from the circular track. Substituting the given numerical values into above, we have \begin{align*} F_c&=\frac{mv^2}{r}\\\\ &=\frac{1000\times 30^2}{100}\\\\&=9000\quad \rm N \end{align*} Thus, the correct answer is (a).

Problem (8): We want to create artificial gravity inside a large rotating hollow cylinder of radius $190\,\rm m$ by rotating it about its longitudinal axis. If we want the magnitude of this artificial gravity to be the same as the normal gravity, the time taken for each rotation of such a system is closest to?

(a) $32\,\rm s$ (b) $28\,\rm s$
(c) $30\,\rm s$ (d) $19\,\rm s$

Solution: Any object in a rotating system experiences a centripetal acceleration whose magnitude is given by $a_c=\frac{v^2}{r}$, where $v$ and $r$ are the tangential constant speed and radius of the circular system (path), respectively.

In this case, we want the magnitude of the artificial gravity to be the same as Earth's gravitational acceleration, which is $g=9.8\,\rm m/s^2$. Substituting this for $a_c$ and solving for $v$, we get the speed required to complete one full circle: \[g=\frac{v^2}{r} \Rightarrow v=\sqrt{gr}\]

We know that each full rotation around a circle of radius $r$ corresponds to traveling a distance equal to the circumference of that circle, i.e., $\ell=2\pi r$. Hence, the time required to complete a full revolution, $T$, is obtained using the definition of average speed $v=\frac{\ell}{t}$, where $t$ is the time taken to cover the distance $\ell$. \[T=\frac{\ell}{v}=\frac{2\pi r}{v}\] Substituting the constant velocity obtained above into this time taken formula, we get: \begin{align*} T&=\frac{2\pi r}{\sqrt{rg}}\\\\ &=2\pi\sqrt{\frac{r}{g}}\\\\ &=2\pi\sqrt{\frac{190}{9.8}}\\\\ &=27.7\quad \rm s\end{align*} In the second line, to eliminate the radical from denominator, we rationalize the fraction by multiplying the numerator and denominator by $\sqrt{r}$. Thus, the correct choice is (b), Because it is closest to the obtained value.

Problem (9): A car moving along a curved track, as shown in the figure below. At the lowest point of the curve, what is the direction of the normal force exerted by the road on the car?

(a) Upward (b) Downward
(c) Forward (d) Backward

a car along a curved road

Solution: When an object is in contact with a surface, the surface exerts a force on the object that is perpendicular to the surface. This force is known as the normal force. At the lowest point of the track, the normal force is directed toward the center of the circular track, which means it is directed upward. Therefore, the correct answer is (a).

Problem (10): A car is moving on a road with many hills and valleys. Assume the radius of these roughnesses to be $R$. At what point on the track, does the driver most likely feel weightlessness?

(a) At the top of the hill when $v=\sqrt{Rg}$.
(b) At the bottom of the valley when $v>\sqrt{Rg}$
(c) At the top of the hill when $v<\sqrt{Rg}$
(d) At the bottom of the valley when $v=\sqrt{Rg}$

Solution: In physics, weightlessness occurs when the object loses contact with the surface, resulting in the normal force becoming zero. At the top of the hill, the normal force is upward, while the weight force is downward. Taking upward as positive and applying Newton's second law, the net force, which is equal to the centripetal force, at the top of the hills is given by: \begin{gather*} mg-F_N=\frac{mv^2}{R} \\\\\Rightarrow F_N=mg-\frac{mv^2}{R}\end{gather*} Similarly, at the bottom of the valley, the net force is: \begin{gather*} F_N-mg=\frac{mv^2}{R} \\\\\Rightarrow F_N=mg+\frac{mv^2}{R}\end{gather*} Keep in mind that the centripetal force is always directed toward the center of the circle; hence, at the hills it is downward, and at the valleys it is upward.

As you can see, the normal force at the valleys can never be zero (it is always the sum of two nonzero forces), but at the hills, it is possible. By setting $F_N=0$ at the hills, we get: \[v=\sqrt{Rg}\] If the car's speed at the top of the hills is equal to this amount, then the driver will experience weightlessness. Hence, the correct answer is (a).

Problem (11): A car is traveling along a curved path of radius $r$ at a constant speed $v$ as shown below. What is the apparent weight of the driver at the bottom of the curved path?

(a) $mg-mv^2/r$ (b) $mg$
(c) $mg+mv^2/r$ (d) none of these

A car is traveling along a curved path of radius r

Solution: the car moves along a circular path, so it undergoes a centripetal force directed toward the center of the circle. As shown in the free-body diagram below, two external forces act on the driver in this position: a downward weight force, and an upward normal force. Taking upward as positive and applying Newton's second law at this point, we have: \begin{gather*} F_N-mg=\frac{mv^2}{r} \\\\ \Rightarrow F_N=mg+\frac{mv^2}{r}\end{gather*} In all AP Physics 1 circular motion problems the apparent weight is synonymous with the normal force. Thus, the correct answer is (c).

Problem (12): A bead is placed on a turntable that is rotating clockwise as in the figure below. Assume after a while, this turntable starts to decrease its spinning speed due to friction in its axis until it ceases. Which arrow best depicts the net force acting on the bead at the instant shown?

(a) $\downarrow$ (b) $\uparrow$
(c) $\searrow$ (d) $\nearrow$
(e) $\rightarrow$

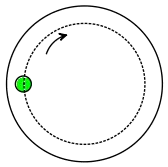
A bead on a turntable

Solution: The bead is rotating, experiencing a centripetal force directed toward the center of the circle. At point $P$, this centripetal force acts rightward.

Simultaneously, the turntable is slowing down, which means an opposing force (such as friction in the axis) must be applied to the bead. At point $P$, the bead's velocity is upward, so the opposing force must be downward to create a deceleration.

Consequently, the resultant of these two force vectors, obtained using the graphical method, is directed downward and to the right ($\searrow$). Hence, the correct answer is (c).

AP Physics: Gravitation Solved Problems

Problem (13): A satellite weighing $M$ takes a time of $T$ to complete a revolution around a planet. Now assume that the satellite had three times as much mass. What changes would occur for the time of circling around the planet at the same altitude?

(a) $2T$ (b) $4T$
(c) $T$ (d) $\frac{T}{2}$

Solution: One of the most common problems on circular motion and gravitation in the AP Physics 1 exam is about whirling a satellite around a planet. In such questions, the inward centripetal force that the satellite experiences is provided by the gravity force between the satellite and the planet. \[\frac{GmM}{r^2}=\frac{mv^2}{r}\] where $m$ and $M$ refer to the masses of satellite and planet, respectively.

Usually, asked for the satellite's speed or period in the orbit. In this question, we consider the case of time orbiting around the planet.

The satellite travels a perimeter of a circle of radius $r$ at a constant speed $v$ in the orbit. This trip takes $T$ which is found using the definition of average speed as below \[T=\frac{2\pi r}{v}\] Substituting this into the previous equation and rearranging it, we get \[T^2=\frac{4\pi^2}{GM}r^3\] This is known as Kepler's third law. As you can see, the mass of the satellite does not appear in the time period formula. Hence, by changing the satellite's mass, its period around the planet does not change. So, the correct answer is (c).

Problem (14): An artificial satellite revolving around the Earth completes each orbit in $120$ minutes. At what altitude is this satellite located in $\rm km$?

(a) $8033$ (b) $9000$
(c) $6033$ (d) $10000$

Solution: The orbital period $T$ of a satellite (or a planet) at altitude $r$ circling around an object of mass $M$ is found using Kepler's third law as below formula \[r^3=\frac{GM}{4\pi^2}T^2\] where with a good approximation we can set, in the AP Physics tests, $\frac{GM}{4\pi^2}=10^{13}$. In this question, the orbital period is given in minutes, which must be converted in seconds by multiplying it by $60$. \[T=120\times 60=7200\,\rm s\] Plugging this into the previous formula and taking the cube root of both sides, we get \begin{align*} r^3 &=\frac{GM}{4\pi^2}T^2\\\\&=10^{13}\times (7200)^2\\\\&=5.184\times 10^{20} \\\\ & \text{Take the cube root of both sides} \\\\ r&=\left(5.184\times 10^{20}\right)^{\frac 13} \\\\ &=8.033\times 10^6\quad\rm m\end{align*} Note that this result is in meters. By dividing it by $1000$ it is converted to $\rm km$. Thus, the answer is $8033\,\rm km$ which is (a).

Problem (15): A satellite with a circular speed of $v$ revolves around a planet of mass $M$. Now assume if the planet had half as much as mass, how would the orbital speed of the satellite change at the same altitude (distance)?

(a) $\frac{v}{\sqrt{2}}$ (b) $\frac{v}{2}$
(c) $\sqrt{2}v$ (d) $2v$

Solution: A satellite moves around a planet in a circular orbit, experiencing an inward centripetal force provided by the gravitational attraction between the Earth and the satellite. Without this gravitational force, the satellite would not be able to orbit. Thus, we have: \begin{gather*} \frac{GmM_E}{r^2}=\frac{mv^2}{r}\\\\ \Rightarrow \quad v=\sqrt{\frac{GM}{r}} \end{gather*} where $m$ is the satellite's mass. As you can see, the satellite's orbital speed is proportional to the square root of the planet's mass, i.e., $v\propto \sqrt{M}$.

Therefore, the ratio the of satellite's speed in two different cases is given by: \begin{gather*} \frac{v'}{v}=\sqrt{\frac{M'}{M}}=\sqrt{\frac{\frac 12 M}{M}}\\\\ \Rightarrow \quad v'=\frac{v}{\sqrt{2}} \end{gather*} where the prime denotes the case when the planet's mass is halved. Hence, if the planet had half as much mass, the satellite's speed in orbit would be a factor of $\frac{v}{\sqrt{2}}$. Therefore, the correct answer is (a).

Problem (16): Assume two planets, say $A$ and $B$, orbiting an unknown star. The planet $A$ is $10$ times farther from the star than planet $B$. The ratio of their speed $\frac{v_A}{v_B}$ is closest to?

(a) $0.4$ (b) $0.2$
(c) $0.3$ (d) $0.5$

Solution: In the previous question, we realized that the speed of an object of mass $m$ orbiting at a distance of $r$ around a mass $M$ is given by \[v=\sqrt{\frac{GM}{r}}\] This formula shows us that the speed in orbit inversely proportional to the square root of the distance from the mass $M$. Thus, their ratio is found to be as below \begin{align*} \frac{v_A}{v_B}&=\sqrt{\frac{r_B}{r_A}}\\\\&=\sqrt{\frac{r_B}{10\,r_B}}\\\\&=\frac{1}{\sqrt{10}}\\\\ &=\boxed{0.31} \end{align*} Hence, the correct answer is (c).

Problem (17): Two bodies attract each other with a force of $F$ gravitationally. Now suppose the masses doubled and the separation between them gets tripled. After these changes, what will the force be?

(a) $4$ (b) $\frac{1}{36}$
(c) $1$ (d) $2$

Solution: According to Newton's universal gravitation law, $F=\frac{m_1 m_2}{r^2}$, the gravitation force between two masses of $m_1$ and $m_2$ is proportional to their product and inversely proportional to the square of the distance between them. Thus, after changes have taken place, the force $F'$ is a factor of as much as the original force $F$ which is found as \begin{align*} \frac{F'}{F}&=\frac{m'_1 m'_2}{m_1 m_2}\times \frac{r^2}{r'^2} \\\\ &=\frac{(\frac 12 m_1)(\frac 12 m_2)}{m_1 m_2}\times \frac{r^2}{(3r)^2}\\\\&=\frac{1}{36}\end{align*} Thus, \[F'=\frac{1}{36}F\] the correct answer is (b).

Problem (18): Consider two small spheres of masses $8\,\rm kg$ and $12\,\rm kg$ that are placed $2\,\rm m$ far away from each other. What is the magnitude of gravitational force between them in $\rm N$? (Take $G=\frac{20}{3}\times 10^{-11}\,\rm \frac{N.m^2}{kg^2}$).

(a) $1.6\times 10^{-8}$ (b) $3.2\times 10^{-8}$
(c) $1.6\times 10^{-9}$ (d) $3.2\times 10^{-9}$

Solution: Two objects of masses $m_1$ and $m_2$ at a center-to-center distance of $r$, attract each other with a gravitational force of magnitude \[F=G\frac{m_1 m_2}{r^2}\] where $\rm G$ is the gravitational constant. Substituting the given values into this formula, we get \begin{align*} F&=G \frac{m_1 m_2}{r^2}\\\\&=\left(\frac{20}{3}\times 10^{-11}\right)\times \frac{8\times 12}{2^2}\\\\&=\boxed{1.6\times 10^{-9}\quad \rm N} \end{align*} Hence, the correct answer is (c).

Problem (19): Two small balls from $20\,\rm m$ from each other, attract one another with a gravitational force of $10^{-8}\rm N$. If one of the balls is $60\,\rm kg$, then what is the mass of the other ball? (Take $G=\frac{20}{3}\times 10^{-11}\,\rm \frac{N.m^2}{kg^2}$)

(a) $10^2$ (b) $10^3$
(c) $5$ (d) $50$

Solution: Apply Newton's law of universal gravitation formula and solve for the unknown mass \begin{gather*} F=G \frac{m_1 m_2}{r^2}\\\\ 10^{-8}=\left(\frac{20}{3}\times 10^{-11}\right)\times \frac{60\times m_2}{20^2} \\\\ \Rightarrow \boxed{m_2=1000\quad\rm kg} \end{gather*} Hence, the correct answer is (b).

Problem (20): The masses of Earth and the Moon are about $5.98\times 10^{24}\rm kg$ and $7.36\times 10^{22}\,\rm kg$, respectively. The separation between them is also $3.84\times 10^8\,\rm m$. The order of magnitude of the gravitational force between those is closest to?

(a) $10^{22}$ (b) $10^{25}$
(c) $10^{28}$ (d) $10^{31}$

Solution: In this problem, the order of magnitude of the force is asked, so it is not necessary to get the full answer. First, determine the order of magnitude of each of the known values, then use the universal gravitation law.

Problem (21): Two small objects of masses $m$ and $2m$ at a distance of $r$ applying a gravitational force of $F$ on each other. How many $F$ times is the magnitude of the gravitational force between two objects of masses $3m$ and $4m$ at a distance of $2r$?

(a) $\frac 13$ (b) $3$
(c) $\frac 23$ (d) $\frac 32$

Solution: According to the universal gravitation law, $F=G\frac{m_1 m_2}{r^2}$, the attraction force between two objects is proportional to the product of their masses and inversely proportional to the square of the distance between them. If we denote the varied masses and distance by prime, then we have \begin{align*} \frac{F'}{F}&=\frac{m'_1}{m_1} \times \frac{m'_2}{m_2} \times \left(\frac{r}{r'}\right)^2 \\\\&=\frac{3m}{m}\times \frac{4m}{2m}\times \left(\frac{r}{2r}\right)^2 \\\\&=3\times 2\times \frac{1}{4}\\\\&=\boxed{\frac 32} \end{align*} Hence, the correct answer is (d).

Problem (22): The plot of the gravitational force between two small objects in terms of distance between them is depicted below. What is $r$ in this plot?

(a) $8$ (b) $12$
(c) $16$ (d) $24$

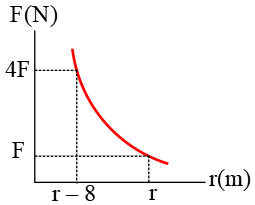
Solution: From the plot, we can find the force between those two masses at an arbitrary distance.

Problem (23): Two similar particles of masses $m$ at a distance of $r$ exert a gravitational force of magnitude $F$ on each other. What percent of the mass of one should be removed and added to the other so that at the previous distance, the magnitude of the gravitational force between them reduces $25\%$?

(a) $75$ (b) $25$
(c) $50$ (d) $33$

Solution: Assume $x$ as much is removed from one and is added to the other. After this manipulation, the masses become $m'_1=m-x$ and $m'_2=m+x$. On the other hand, the force between them $F'$, as a result, gets reduced $25\%$ as much as the original force $F$. This means \[F'=F-0.25F=0.75F\] Now, form their ratio and apply universal gravitation law to find the unknown $x$ \begin{gather*} \frac{F'}{F}=\frac{m'_1}{m_1}\times \frac{m'_2}{m_2} \\\\ \frac 34=\frac{m-x}{m}\times \frac{m+x}{m}\\\\ \frac{3}{4}=\frac{m^2-x^2}{m^2}\\\\ 3m^2=4m^2-4x^2 \\\\ \Rightarrow 4x^2=m^2 \\\\ \Rightarrow x=\frac{m}{2} \end{gather*} This computation shows us that we must subtract by $50\%$ from one and add to the other. Thus, the correct answer is (c).

Problem (24): Imagine a point between the Moon and Earth where if an object is placed there, the net force applied on it from the Moon and Earth is zero. How many times is the distance of that point from the Earth's center relative to the Moon's center? (Take Earth's mass to be $81$ times the Moon's mass).

(a) $9$ (b) $10$
(c) $80$ (d) $81$

Solution: Assume the point lies at a distance of $r_E$ from the Earth and $r_M$ from the Moon. We want at this point the gravitational force on an imaginary mass $m$ is zero. So, the gravitational forces $F_E$ from the Earth and $F_M$ from the Moon on $m$ must be balanced.

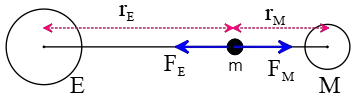
A mass point between the Earth and the Moon

\begin{gather*} F_E=F_M \\\\ \frac{GmM_E}{r_E^2}=\frac{GmM_M}{r_M^2} \\\\ \Rightarrow \frac{M_E}{r_E^2}=\frac{M_M}{r_M^2}\\\\ \rm{set \ M_E=81M_M} \\\\ \Rightarrow \frac{81M_M}{r_E^2}=\frac{M_M}{r_M^2} \\\\ \Rightarrow r_E^2=81\times r_M^2 \\\\ \Rightarrow \boxed{r_E=9r_M}\end{gather*} Hence, the correct answer is (a).

Problem (25): A spacecraft of mass $3\times 10^4\,\rm kg$ is in between the distance of Earth and the Moon. What is the net gravitational force applying on this spacecraft at this location? (Take the Earth's mass, $6\times 10^{24}\,\rm kg$, the Moon's mass $7.5\times 10^{22}\,\rm kg$, the distance between Earth and the Moon $4\times 10^5\,\rm km$, and $G=\frac{20}{3}\times 10^{-11}\,\rm \frac{N.m^2}{kg^2}$)

(a) $303.75$ (b) $296.25$
(c) $607.5$ (d) $592.5$

Solution: The spacecraft is positioned halfway between the Earth and the Moon. Thus, its distance from both is \[d=\frac{4\times 10^5}{2}=2\times 10^5\rm km\] Now, using the universal gravitational law find the force exerted by the Earth and the Moon on the spacecraft.

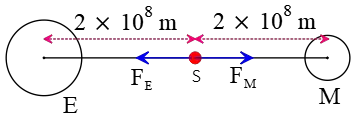
Spacecraft between the Earth and the Moon

\begin{align*} F_E&=G\frac{M_E m}{d^2}\\\\ &=\left(\frac{20}{3}\times 10^{-11}\right)\times \frac{(3\times 10^4)(6\times 10^{24})}{4\times 10^{16}}\\\\&=3\times 10^2 =300\,{\rm N} \\\\ F_M&=G\frac{M_M m}{d^2}\\\\ &=\left(\frac{20}{3}\times 10^{-11}\right)\times \frac{(3\times 10^4)(7.5\times 10^{22})}{4\times 10^{16}}\\\\&=3.75\,{\rm N} \end{align*} These two forces on the spacecraft are in the same line but in opposite direction, so the net force applying on the spacecraft is their subtraction. \begin{align*} F_{net}&=F_E-F_M \\\\ &=300-3.75\\\\&=\boxed{296.25\quad {\rm N}}\end{align*} Thus, the correct answer is (b).

Problem (26): The ESA wants to design a satellite to orbit around Earth $5$ times a day. What would be the radius of its orbit in $\rm m$, neglecting the presence of the Moon? (Assume $G=6.67\times 10^{-11}\,\rm \frac{N.m^2}{kg^2}$, and $M_{earth}=5.97\times 10^{24}\,\rm kg$)

(a) $3.45\times 10^7$ (b) $1.44\times 10^7$
(c) $2.11\times 10^7$ (d) $0.69\times 10^7$

Solution: '' $5$ times a day'' means $5$ full revolution every $24$ hours. Thus, one full revolution takes $\frac{24}{5}$ hours or $\frac{24}{5}\times 3600$ in seconds. This is the time period of this designed satellite. Now, apply Kepler's third law of motion to find the radius of orbit \begin{align*} r^3 &=\frac{GM}{4\pi^2}T^2\\\\&=10^{13}\times \left(\frac{24}{5}\times 3600\right)^2 \\\\ & \text{Take the cube root of both sides} \\\\ r&=1.44\times 10^7\quad \rm m \end{align*} Keep in mind that in all the AP physics gravitation questions, we can set $\rm \frac{GM}{4\pi^2}=10^{13}$ with a good approximation. Thus, the correct answer is (b).

Note: the formula of cube root is \[a=\sqrt[3]{b} \ \text{or} \ a= b^{\frac 13}\]

Author: Dr. Ali Nemati
Published: 1/1/2022