Conservation of Momentum: Problems with Explanations
Here, we want to examine the law of conservation of momentum with numerous solved practice problems. All these solved questions are for high school and college students.
One of the other forms/statements of Newton's second law is written as $F_{net}=\frac{\Delta p}{\Delta t}$ where $F_{net}$ is the net external force acting on a system. $\Delta p$ is the change in the momentum of the system after applying a net force on it.
If $F_{net}=0$ it follows that $\Delta p=0$. That means there is no change in the momentum of the system.
As a result, the momentum of the system stays at all times the same. This statement is expressed as the law of conservation of momentum.
After this very brief introduction, we are going to learn more deeply by solving a ton of practice problems.
The Law of Conservation of Momentum: Problems
Problem (1): A $1500-\rm kg$ car traveling at $7\,\rm m/s$ strikes another car of mass $2000\,\rm m/s$ at rest at a stop light. After colliding, the cars get locked together. What is the final velocity of the cars?
Solution: Take the two cars as a combined system. In this case, the rear car exerts a force on the front car. According to Newton's third law, the front car also applies a force of the same magnitude but in the opposite direction.
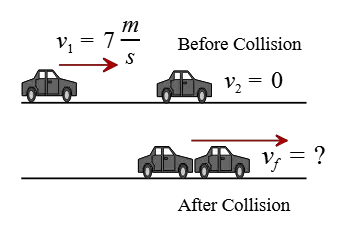
To these two cars, as a whole, no external forces, say friction or force due to pushing by a person, are applied. Those two forces between the cars are called internal forces and cannot change the momentum of an object.
Before the colliding, the front car is at rest, $v_2=0$ and its initial momentum is also $m_2 v_2=0$.
After the colliding, the two cars have a common speed of $v_f$ in the same direction with a combined mass of $m_1+m_2$.
After these explanations, we apply the conservation of momentum as below \begin{gather*} p_{before}=p_{after} \\\\ m_1 v_1 +m_2 v_2= (m_1 + m_2)v_f \end{gather*} This is the mathematical statement of momentum conservation law. Now, solving for the unknown speed $v_f$ yields \begin{align*} v_f &=\frac{m_1 v_1}{m_1 + m_2} \\\\ &=\frac{1500\times 7}{1500+2000} \\\\ &=\boxed{3\quad\rm m/s} \end{align*} Therefore, the two cars stick together and move with a common speed of $3\,\rm m/s$.
Isn’t this content as valuable as a $10 private class? Please support me here.
Problem (2): A $\rm 77-kg$ man holds a $30-\rm N$ rifle and shoots a $4\,\rm g$ bullet with a speed of $450\,\rm m/s$.
(a) With what speed does the rifle recoil?
(b) If the rifle is held firmly by the man, how fast do the man and the rifle recoil?
Solution: In this problem of the conservation law of momentum, we want to understand more about systems.
(a) In this part, we can take the rifle and its bullet as an isolated system meaning that we separate those from the man. Again, aside from the internal forces between the rifle and the bullet, no external forces are acting upon them.
Thus, the net external force is zero and their momentum before and after the shooting is the same, or in other words, the momentum of the system is conserved.
But recall from the section on momentum and impulse problems that momentum is a vector quantity in physics having a magnitude (speed) and a direction.
Thus, the correct form of momentum conservation must be written in the vector form as follows \[\vec{p}_{before}=\vec{p}_{after}\] Now take the right as the positive $x$ direction.
With this choice, the bullet moving to the right has a positive velocity $\vec{v}_b=+v_b$, and the rifle recoils to the left with a negative velocity $\vec{v}_r=-v_r$ where $v_b$ and $v_r$ are the speed (magnitude) of the velocity vectors.
Before shooting, the system (bullet + rifle) is at rest, so its momentum is zero, i.e., $\vec{p}_{before}=0$.
Applying the law of conservation of momentum, we get \begin{gather*} \vec{p}_{before}=\vec{p}_{after} \\\\ 0= m_b\vec{v}_b+m_r \vec{v}_r \\\\ m_b v_b + m_r (-v_r) =0 \\\\ \Rightarrow \, v_r=\frac{m_b v_b}{m_r} \end{gather*} By substituting the numerical values into this, we get the recoiling speed of the rifle as below \begin{align*} v_r &=\frac{0.004\times 450}{3} \\\\ &=\boxed{0.6\,\rm m/s} \end{align*} where the definition of weight, $W=mg$, is used to find the rifle's mass.
Hence, without the help of the shooter, if applicable, the rifle recoil with a speed of $0.6\,\rm m/s$.
(b) Now, extend the system to include the man so our new system is man+rifle+bullet. Again, no external forces are acting on the system so the momentum stays the same.
The system initially is at rest, so its momentum is zero, i.e., $\vec{p}_{before}=0$. After shooting, the shooter and the rifle recoil at a common speed of $\vec{V}_r=-V$ to the left. Therefore, we have \begin{gather*} \vec{p}_{before}=\vec{p}_{after} \\\\ 0= m_b\vec{v}_b+(m_r+m_s) \vec{V} \\\\ m_b v_b + (m_r+m_s)(-V) \\\\ \Rightarrow V=\frac{m_b v_b}{m_r+m_s} \end{gather*} Substituting the known values into this, get\begin{align*} V&=\frac{m_b v_b}{m_r+m_s} \\\\ &=\frac{0.004\times 450}{3+77} \\\\ &=\boxed{0.02\,\rm m/s}\end{align*}
Problem (3): A $15\,\rm g$ bullet moving at a speed of $350\,\rm m/s$ hits a wood block of mass $M=2\,\rm kg$ and remains in it. How fast will the block and bullet move after the collision?
Solution: First of all, in all conservation of momentum problems, consider a system. In this case, the bullet and the block are assumed to be an isolated system. No external forces are acting on them, so the momentum is conserved.
After the collision, those two have a common speed of $V$. Since before and after the collision both the bullet and the wood block travel in the same direction, there is no need to use the vector form of the conservation law of momentum. Hence, we have \begin{gather*} p_{before}=p_{after} \\\\ m_b v_b + Mv_w=(m_b+M)V \\\\ \Rightarrow V=\frac{m_b v_b}{m_b+M} \end{gather*} The wood block is initially at rest so $v_w=0$. Substituting the values into this we get \begin{align*} V&=\frac{m_b v_b}{m_b+M} \\\\ &=\frac{0.015\times 350}{0.015+2} \\\\ &= \boxed{2.6\,\rm m/s}\end{align*}
Problem (4): A $8500-\rm kg$ railroad car traveling at a speed of $24\,\rm m/s$ strikes another $7500\,\rm kg$ car at rest. After striking, the two cars stick together and move with a combined speed of $10\,\rm m/s$. What is the mass of the second car?
Solution: Write the conservation of momentum equation for the $x$-direction as below \begin{gather*} p_i=p_f \\\\ m_1 v_1 + m_2 v_2 =(m_1+m_2)V \end{gather*} where $p_i$ and $p_f$ are the momenta (plural form of momentum) before and after the collision. Substituting the values into this and solving for the unknown mass of the second car $m_2$ yields \begin{gather*} (8500)(24)+(7500)(0)+(8500+7500)V \\\\ \Rightarrow \boxed{V=12.75\,\rm m/s} \end{gather*}
Problem (5): A $80\,\rm kg$ man standing on a negligible friction surface, throws a $48\,\rm g$ stone away from himself in a horizontal direction and gives it a speed of $5\,\rm m/s$. What speed does the man acquire after this action?
Solution: The system is the man + the stone. Since the man standing on a frictionless surface, no external forces act on it. As a result, the momentum of the system must remain constant before and after throwing the stone.
Let $m_1$ and $v_1$ be the man's mass and velocity after throwing the stone and $m_2$ and $v_2$ the stone's mass and velocity. Before throwing the stone, both the man and the stone are at rest, so the initial momentum of the system is zero, $p_i=0$.
Applying the conservation of momentum in the $+x$-direction, we have \begin{gather*} \vec{p}_i=\vec{p}_f \\\\ 0 = m_1 \vec{v}_1+m_2 \vec{v}_2 \\\\ 0=(80) \vec{v}_1+(0.048)(5) \\\\ \Rightarrow \boxed{\vec{v}_1=-0.003\,\rm m/s} \end{gather*} The negative sign on the man's velocity after throwing the stone indicates that the man moves in opposite direction of the stone's velocity, in accordance with Newton's third law of motion.
Thus, the man moves back with a speed of $0.003\,\rm m/s$ toward the negative $x$-direction.
Problem (6): An object has a momentum of $45\,\rm kg\cdot m/s$ and collides with a stationary object and makes it start to move. If the momentum of the first object is reduced to $25\,\rm kg\cdot m/s$, what momentum does the second object gain?
Solution: This is another type of conservation of momentum problem. As you can see, in such cases, the only word is the momenta of objects.
The initial momenta of object are \begin{align*} p_i&=p_{i1}+p_{i2} \\ &=45+0 \end{align*} And similarly, the final momenta are \begin{align*} p_f &=p_{f1}+p_{f2} \\&=25+p_{f2} \end{align*} According to the the laws of conservation of momentum, $p_i=p_f$, where $p_i$ and $p_f$ are the momenta of the objects before and after the collision, hence \begin{gather*} p_i=p_f \\ 45+0=25+p_{f2} \\ \Rightarrow \boxed{p_{f2}=20\,\rm kg\cdot m/s} \end{gather*} Therefore, the second object, initially at rest, absorbs $20\,\rm kg\cdot m/s$ of the first object.
Problem (7): Two freight cars, having a mass of $2.5\times 10^3 \,\rm kg$ collide and stick together. Before the colliding, one is traveling at $3.5\,\rm m/s$ and the other is at rest. What is their final speed?
Solution: Consider the two cars together as an isolated system, meaning that no external forces act on them such as friction.
It was said that the two cars stick together after colliding so they have a common speed, $V$. Applying the laws of conservation of momentum, we get \begin{gather*} p_i=p_f \\\\ m_1 v_1+m_2v_2=(m_1+m_2)V \\\\ \Rightarrow V=\frac{m_1v_1+m_2v_2}{m_1+m_2} \end{gather*} Substitute the given values into this as below \begin{align*} V&=\frac{(2.5\times 10^3)(3.5)+0}{2(2.5\times 10^3)} \\\\ &=\boxed{1.75\,\rm m/s} \end{align*}
Problem (8): A $0.25\,\rm kg$ ball traveling at $5\,\rm m/s$ collides head-on with another ball with a mass of $2\,\rm kg$ that is moving at $8\,\rm m/s$ in the opposite direction. After colliding, the $0.25\,\rm kg$ ball recoils at $15\,\rm m/s$. What is the speed and direction of the second ball after the collision?
Solution: This is a challenging problem on the laws of conservation of momentum. According to this law, equate the initial momenta of the object with the final momenta.
Notice that since the two objects are moving toward each other, the velocity of one of them must be accompanied by a negative sign. Assume the right to be the positive direction.
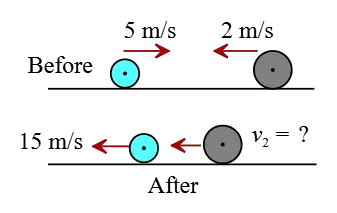
Write the momentum conservation and solve for the final velocity of the second ball $v_{f2}$ as below \begin{gather*} \vec{p}_i=\vec{p}_f \\\\ m_1 \vec{v}_{i1}+m_2 \vec{v}_{i2}=m_1 \vec{v}_{f1}+m_2 \vec{v}_{f2} \\\\ \Rightarrow \vec{v}_{f2}=\frac{m_1 \vec{v}_{i1}+m_2 \vec{v}_{i2}-m_1 \vec{v}_{f1}}{m_2} \end{gather*} Substituting the numerical values into this, gives \begin{align*} \vec{v}_{f2}&=\frac{(0.25)(5)+(2)(-8)-(0.25)(-15)}{2} \\\\ &=\boxed{-5.5\,\rm m/s} \end{align*} The negative sign in the laws of conservation of momentum indicates the object moves in the opposite direction of our assumed positive direction.
Therefore, the second ball, moving initially to the west, after colliding continues its movement in the same direction. This result is reasonable, as the second ball has much greater initial momentum than the first ball.
Consequently, the second ball moves toward the west at about $5.5\,\rm m/s$ after the collision or both the ball moves in the same direction at different speeds.
Problem (9): Two crates of massed $1.5\,\rm kg$ and $2.5\,\rm kg$ are connected together with a light-compressed spring. After releasing the spring, the crates move in opposite directions. The $1.5\,\rm kg$ would also move at $25\,\rm cm/s$ toward the left. What is the velocity of the $2.5\,\rm kg$ crate?
Solution: Assume the two cars and the compressed spring between them to be an isolated system. By choosing this way, no external forces are exerted on the system except the internal forces due to the spring force pushing apart the crate in the opposite direction.
Take the right as the positive direction, so the velocity of $m_1=1.5\,\rm kg$ crate is written as $v_1=-25\,\rm cm/s$. Initially, the crates are at rest, so the initial momentum of the system is zero, i.e., $\vec{p}_i=0$.
Notice that here the velocity is given in $\rm cm/s$ and must be converted into the SI units of velocity $\rm m/s$ as below \begin{align*} v_1 &=-25\,\rm \frac{cm}{s} \times \left(\frac{0.01\,\rm m}{s}\right) \\\\ &=-0.25\,\rm m/s \end{align*}
Applying the momentum conservation and solving the velocity of the $2.5\,\rm kg$ crate gives us \begin{gather*} \vec{p}_i=\vec{p}_f \\\\ 0=m_1 \vec{v}_1+m_2 \vec{v}_2 \\\\ \Rightarrow \vec{v}_2=-\frac{m_1}{m_2}\vec{v}_1 \end{gather*} Substituting the given values get \begin{align*} \vec{v}_2 &=-\left(\frac{1.5}{2.5}\right)(-0.25) \\\\ &=\boxed{0.15\,\rm m/s} \end{align*} The obtained positive result shows that the other crate must be pushed toward the right with a speed of $0.15\,\rm m/s$, as expected.
As an exercise, we convert this speed written in $\rm cm/s$ by multiplying by $100$ into the SI unit of speed $\rm m/s$. \[v_2=15\,\rm m/s\]
Problem (10): A series of stroboscopic photographs, shows a $215\,\rm g$ gulf club moving at $55\,\rm m/s$ immediately before striking a $46\,\rm g$ golf ball on a tee. After the collision, the club moves at $42\,\rm m/s$ in the same direction as before striking. What is the speed of the golf ball after impact?
Solution: If we assume that there are no external forces on the golf club + golf ball (as our system), we can apply the conservation law of momentum to solve this practice problem.
Take the mass and velocity of the golf club as $m_1$ and $v_1$, respectively, and $m_2$ and $v_2$ the golf ball's mass and velocity. We expect, which is reasonable, that the golf club and ball travel in the same direction after colliding, so we can relax the vector form of momentum conservation. \begin{gather*} p_i=p_f \\\\ m_1 v_{1i}+m_2 v_{2i} = m_1 v_{1f}+m_2 v_{2f} \\\\ \Rightarrow v_{2f}=\frac{m_1 (v_{1i}- v_{1f})}{m_2} \end{gather*} where in above we set the initial speed of the golf's ball zero, $v_{2i}=0$. Substituting the numerical values into this, we get \begin{align*} v_{2f}&=\frac{(0.215)(55-42)}{0.046} \\\\ &=\boxed{60.7\,\rm m/s} \end{align*} Therefore, the golf ball start moving at about $60\,\rm m/s$ in the same direction of the golf club.
Problem (11): A $85\,\rm kg$ fisherman jumps from a dock onto a $135\,\rm kg$ rowboat resting on the west side of the dock. Assume just before jumping and leaving the dock, he has a horizontal speed of $4.3\,\rm m/s$ toward the west. What is the final velocity of the boat and the fisherman?
Solution: We take the fisherman and the rowboat as an isolated system and the west as our positive $x$ direction. With this choice, the fisherman's velocity is $\vec{v}_1=4.3\,\rm m/s$. Assuming no external forces (an assumption made in all conservation law problems), we can apply the conservation law of momentum as follows to find their final velocity, $V$. \begin{gather*} \vec{p}_i=\vec{p}_f \\\\ m\vec{v}_1+M\vec{v}_2=(M+m)\vec{V} \\\\ (85)(4.3)+0 = (85+135) \vec{V} \\\\ \Rightarrow \boxed{\vec{V}=-1.6\,\rm m/s} \end{gather*} where the dock's velocity is set zero, $\vec{v}_2=0$. The negative sign shows that the final combination travels in the opposite direction of our chosen coordinate system. Thus, the boat and the fisherman, as a whole, move to the east at a speed of about $1.6\,\rm m/s$.
Problem (12): A $24-\rm kg$ child throws a package out horizontally at a speed of $10\,\rm m/s$ while standing on a $35-\rm kg$ skateboard over a rough frictionless surface. Find the velocity of the skateboard immediately after throwing the package, assuming the child and skateboard were initially at rest.
Solution: the surface is frictionless, so no external forces act on our system including skateboard+package. Hence, the momentum of the system before and after throwing must be the same, or the momentum is conserved.
The system is initially at rest so $p_i=0$. Take the right to be the $+x$ direction and assume the package is thrown to the right, i.e., $\vec{v}_1=10\,\rm m/s$. Let the mass and velocity of the skateboard be $m_2$ and $\vec{v}_2$. Applying the momentum conservation, we get \begin{gather*} \vec{p}_i=\vec{p}_f \\\\ 0=m_1 \vec{v}_1+m_2 \vec{v}_2 \\\\ 0=(24)(10)+(35) \vec{v}_2 \\\\ \Rightarrow \boxed{\vec{v}_2=-6.86\,\rm m/s} \end{gather*} The negative shows that just after throwing the package out toward the right, the skateboard also moves in the opposite direction to conserve the momentum of the system.
Thus, the skateboard travels to the left at a speed of about $6.8\,\rm m/s$.
Problem (13): A $22-\rm g$ bullet fired from a rifle at a speed of $240\,\rm m/s$ penetrates a wooden block of mass $2\,\rm kg$ and exits with a speed of $150\,\rm m/s$. Assume the block is initially stationary on a frictionless surface. With what speed does it move after the bullet emerges?
Solution: Like other momentum conservation law problems, first take a positive direction, say the $+x$ axis. The bullet initially travels in this direction so its velocity is written as $\vec{v}=+240\,\rm m/s$. Now assume the mass and velocity of the block designated by $M$ and $\vec{V}$, respectively, and the emerging velocity of the bullet to be $\vec{v}'=150\,\rm m/s$ in the same direction as the original. According to the laws of conservation of momentum, we have \begin{gather*} \vec{p}_i=\vec{p}_f \\\\ m\vec{v}=m\vec{v}'+M\vec{V} \\\\ \Rightarrow \vec{V}=\frac{m(\vec{v}-\vec{v}')}{M} \end{gather*} Substituting the numerical values into this expression, we will have \begin{align*} \vec{V}&=\frac{(0.022)(240-150)}{2} \\\\ &= \boxed{-0.99\,\rm m/s} \end{align*} Notice that the block is initially at rest, and its initial momentum is zero.
Therefore, the wooden block will return at a speed of $0.99\,\rm m/s$.
Summary:
In this complete guide, we solved some problems about the law of conservation of momentum.
We learned that when there is no net external force on an isolated system, the momentum of the system before and after some event, like an explosion or collision, remains constant. \[\vec{p}_i=\vec{p}_f\]
An isolated system is also defined as a system in which no external forces, such as gravitational force or friction, act on the system.
Author: Dr. Ali Nemati
Published: 9/3/2022
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
