Converging (Convex) Lens Problems with Answers For High Schools
A converging (or convex) lens is defined as an optical instrument that converges a group of rays parallel to the optical axis to a point on the other side of the lens.
The image distance $d_i$ and object distance $d_o$ are related together by the thin-lens equation \[\frac 1f=\frac 1d_o+\frac 1d_i\] where $f$ is the focal length of the lens.
The orientation and size of the image are also found by the magnification formula \[M=-\frac{d_i}{d_o}=\frac{h_i}{h_o}\] where $h_i, h_o$ are the heights of the image and object, respectively.
Sign conventions for converging lenses:
(1) The focal length is always positive.
(2) For a real image, the image distance is positive, and it is negative for a virtual one.
(3) The absolute value of the magnification shows the amount of change in image size relative to the object.
(4) A negative magnification ($M<0$) is an indication of an inverted image, and for $M>0$, we have an upright image.
Converging (convex) Lens Problems:
Problem (1): A candle is placed at a distance of 30 cm from a converging lens having a focal length of 10 cm.
(a) At what distance from the lens is the candle's image formed?
(b) Is this image real or virtual?
(c) Is this image upright or inverted?
(d) Draw a ray diagram for this configuration and verify the above results.
Solution: The known data is: the object distance $d_o=30\,{\rm cm}$ and the focal length $f=+10\,{\rm cm}$. All that is needed is to use the thin-lens equation and magnification formula.
(a) Solving the thin-lens equation below for the unknown image distance $d_i$, we have \begin{align*} \frac 1f&=\frac 1d_o+\frac 1d_i \\\\ \frac 1{10}&=\frac{1}{30}+\frac{1}{d_i}\\\\\Rightarrow \frac{1}{d_i}&=\frac{1}{10}-\frac{1}{30}\\\\&=\frac{3-1}{30}=\frac{2}{30} \end{align*} Inverting the above expression, get the image distance as $d_i=+15\,{\rm cm}$.
(b) Because the image distance was obtained positively, the candle's image is real and formed on the backside of the lens.
In other words, the image is formed on the opposite side of the lens where the object is present. This is the definition of a real image formed by a converging (convex) lens.
(c) The magnification formula for a thin lens, which is negative of the ratio of image distance to object distance, gets the orientation of the image formed. \[M=-\frac{d_i}{d_o}\]
A negative magnification, $M<0$, indicates an inverted image, and for $M>0$, an upright image is formed.
In this example problem, we have \[M=-\frac{d_i}{d_o}=-\frac{+15}{30}=-0.5\] A negative magnification is obtained, so the candle's image is inverted.
(d) All the above results are also obtained by a ray diagram shown below.
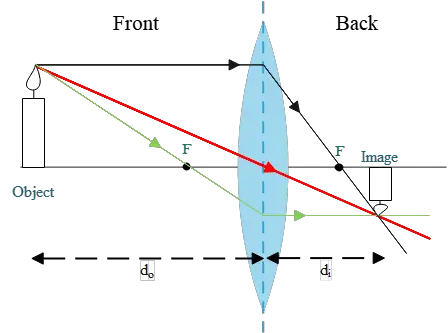
Problem (2): An object, 12 cm tall, is placed 4 cm in front of a converging (double convex) lens having a focal length of 12 cm.
(a) Locate the image graphically by drawing a ray diagram.
(b) Find the image distance.
(c) Determine the image size and its orientation
Solution: Given quantities are
Object height $h_o=12\,{\rm cm}$,
Object distance $d_o=4\,{\rm cm}$,
Focal length $f=+12\,{\rm cm}$,
(a) By substituting the above data into the thin lens equation, and solving for the unknown image distance, we get \begin{align*} \frac 1f&=\frac 1d_o+\frac 1d_i \\\\ \frac 1{12}&=\frac{1}{4}+\frac{1}{d_i}\\\\\Rightarrow \frac{1}{d_i}&=\frac{1}{12}-\frac{1}{4}\\\\&=\frac{1-3}{12}=\frac{-2}{12} \end{align*} Then, the image distance is $d_i=-6\,{\rm cm}$. It is negative, so we conclude that the image is virtual and formed behind the lens at a distance of 6 cm from it.
The ray-tracing diagram for this configuration is also drawn below.
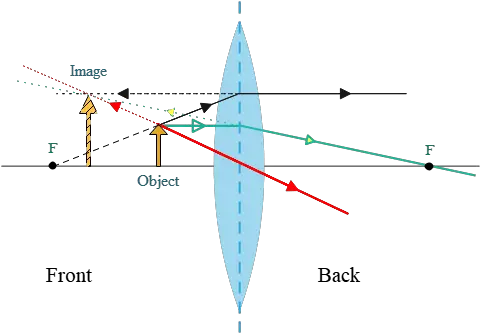
(b) The magnification formula for the lens gives the orientation and size of the image formed. Recall that the magnification formula for thin lenses is written as below \[M=-\frac{d_i}{d_o}=\frac{h_i}{h_o}\] where $h_i$ and $h_o$ are the heights of the image and distance. Therefore, \begin{align*} -\frac{d_i}{d_o}&=\frac{h_i}{h_o} \\ \\ -\frac{-6}{4}&=\frac{h_i}{12}\\\\ \Rightarrow h_i&=-18\quad {\rm cm}\end{align*} There are two notes about this result. First, the minus sign indicates the orientation of the image, which is inverted.
And the other is its absolute value, which, in this case, is greater than one.
Consequently, the image formed is inverted and larger in size.
The lesson that we learned from this example problem is that a converging lens is a magnifying glass when an object is placed within its focal length.
Problem (3): A person who wants to be able to see an ant holds it 4 cm from a 6 cm-focal-length magnifying glass.
(a) Find the magnification of the lens used in the magnifying glass?
(b) Explain how a ray diagram is sketched.
Solution: Known data are object distance and focal length, $d_o=4\,{\rm}$ and $f=+6\,{\rm cm}$, respectively.
(a) Using the thin lens equation and solving for the image distance, we get \begin{align*} \frac 1f&=\frac 1d_o+\frac 1d_i \\\\ \frac 1{6}&=\frac{1}{4}+\frac{1}{d_i}\\\\\Rightarrow \frac{1}{d_i}&=\frac{1}{6}-\frac{1}{4}\\\\&=\frac{2-3}{12}=\frac{-1}{12} \end{align*} By solving the above expression, we have $d_i=-12\,{\rm cm}$. It is negative, so the image is virtual and formed on the side where the object is present, which is in front of the lens!
Lateral magnification is negative of the ratio of the image distance to the object distance, $M=-d_i/d_o$.
This formula has two parts: one is its absolute value, which says how much an object gets magnified or de-magnified
The other is its sign, which clarifies the orientation of the image relative to the object, i.e., whether the image is upright or inverted.
Therefore, using this magnification formula, we can find both the orientation and the size of the image formed. \[M=-\frac{d_i}{d_o}=-\frac{-12}{4}=+3\]
Hence, the image is three times as large as the object and upright because $M$ is a positive number.
(b) Drawing a ray-tracing diagram also verifies the above result. To sketch such a diagram we need the following ingredients:
(i) An arrow is a representative of the object.
(ii) An optical axis and a converging lens.
(iii) Three special rays, as below, emanating from a point on the object, say the tip of an arrow.
The first is parallel to the axis and refracts through the far focal point.
The second is through the focal point and exits parallel to the axis.
The third is through the center of the lens without any deflection.
The keynote is that all refracted rays must converge to a point. If the exit rays diverge, then we must trace back those rays to meet each other at a point.
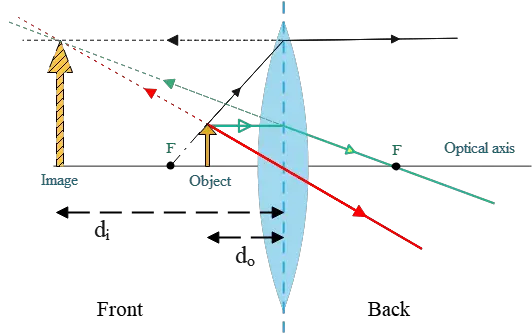
As you can see, all exit rays diverge in this problem, but their tracing back converges and makes the tip of the arrow, which is the image location.
Problem (4): We place an object at a distance of 50 cm from our eyes. (a) Where should a converging lens of focal length 10 cm be placed to again form an image on our retina's eyes? (b) What is the magnification of this lens?
Solution: Here, the only parameter given is the distance between the object and its image. Recall that images can be formed in front of or behind a converging lens.
Once the image is virtual, formed in front of the lens, the distance between the image and object is written as $d_i-d_o$ (see the figures of the previous problems).
But when the image is real, it is formed behind the lens, so the distance between the image and the object is $d_i+d_o$.
Another important note is that a real image is always formed on a screen, say a blank canvas or our eye's retina.
(a) All the above things together say that $d_i+d_o=50\,{\rm cm}$ and hence $d_i=50-d_o$. The focal length is also $f=+10\,{\rm cm}$. Using the thin lens equation, we have \begin{align*} \frac 1f&=\frac 1d_o+\frac 1d_i \\\\ \frac 1{10}&=\frac{1}{d_o}+\frac{1}{50-d_o}\\\\\Rightarrow \frac{1}{d_i}&=\frac{1}{d_o}-\frac{1}{50-d_o}\\\\&=\frac{50}{d_o(50-d_o)}\end{align*} Rearranging the above expression, we get a quadratic equation with the form of $ax^2+bx+c=0$ whose solutions are as below \[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\] Solving the above equation for the object distance $d_o$, we have \[d_o=\frac{-(-50)\pm\sqrt{(-50)^2-4(1)(500)}}{2(1)}\] Simplifying the above, gives $d_o=13.82\,{\rm cm}$ or $d_o=36.18\,{\rm cm}$. Thus, the converging lens should be placed at a distance of about 14 cm or 36 cm from the object.
(b) Using the magnification formula, we have \[M_1=-\frac{d_i}{d_o}=-\frac{50-13.82}{13.82}=-2.61\]
or when the lens is placed 36.18 cm in front of the lens, gives a magnification of \[M_1=-\frac{d_i}{d_o}=-\frac{50-36.18}{36.18}=-0.38\] In both cases, the negative magnification shows an inverted image formed on the retina.
Author: Ali Nemati
Date Published: 5/22/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
