Dielectrics: Solved Problems for AP Physics C Exam
In this article, you will learn how to solve dielectric problems in a step-by-step strategy. All these solved questions are helpful for the AP Physics C exam as well.
Dielectric Practice Problems
Problem (1): A pair of circular plates with a radius of $5\,\rm cm$ separated by $2\,\rm mm$ is filled with a piece of plastic having $\kappa=2.6$.
(a) What is its capacitance?
(b) Find its capacitance without the insulator between the plates.
Solution: The capacitance of an insulator-filled parallel plate capacitor is determined by the following formula \[C=\frac{\kappa \epsilon_0 A}{d}\] where $\kappa$ is the dielectric constant of the insulator material, $A$ is the area of the plates, and $d$ is the spacing between the plates.
(a) The circular plates have a surface area of \begin{align*} A&=\pi r^2 \\&=\pi \times (0.05)^2 \\&=15.7\times 10^{-4} \end{align*} Put the given values into the insulator-filled parallel-plate capacitor formula and solve for $C$ \begin{align*} C&=\frac{\kappa \epsilon_0 A}{d}\\\\ &=\frac{(2.6)(8.85\times 10^{-12})(15.7\times 10^{-4})}{2\times 10^{-3}} \\\\ &=18.06\,\rm pF\end{align*}
(b) The capacitance of a vacuum-gaped (or air) parallel-plate capacitor is given by $C_0=\frac{\epsilon_0 A}{d}$. This is the same formula as the previous part, except that $k$ is replaced by $1$, the dielectric constant of the vacuum.
By comparison between the two formulas, we find out that the presence of a dielectric between the plates of a capacitor increases the capacitance by the factor $k$, \[C=kC_0\] Therefore, the capacitance of this capacitor with air between the plates, $C_0$, is \begin{align*} C_0&=\frac{C}{k} \\\\ &=\frac{18.06\times 10^{-12}}{2.6} \\\\ &=6.94\,\rm pF\end{align*}
Problem (2): A piece of material with a dielectric constant of $2.5$ is inserted between the plates of a $6-\rm \mu F$ capacitor while it is connected to a power supply that keeps a potential difference of $36\,\rm V$ across the plates.
How much energy is stored in the capacitor before and after the insertion of the dielectric?
Solution: One of the applications of a capacitor is to store electric energy as electric potential energy. This potential energy is equal to the work done by the battery to separate $+$ and $-$ charges and store them on each plate of the capacitor.
The amount of electric potential energy stored in a capacitor is given by one of the following equivalent expressions \[\rm P.E.=\frac 12 Q\Delta V=\frac 12 C (\Delta V)^2=\frac{Q^2}{2C}\] where $\Delta V$ is the potential difference between the plates when the capacitor is fully charged.
We use the equation $\rm P.E=\frac 12 CV^2$ because we are given $C$ and $V$. Before insertion of dielectric, we have \begin{align*} \rm P.E.&=\frac 12 C_0 V^2 \\\\ &=\frac 12 (6\times 10^{-6})(36)^2 \\\\ &=3.8\,\rm mJ\end{align*} In this problem, while the capacitor is connected to the battery an insulator is placed between the plates. As a result, the voltage across the capacitor remains unchanged, but its capacitance and the charge stored on each plate change.
In this case, the capacitance increases by a factor of $k$, the dielectric constant of that insulator. \begin{align*} C&=\kappa C_0\\ &=2.5\times 6\\ &=150\,\rm \mu F\end{align*} Thus, after insertion of dielectric we have \begin{align*} \rm P.E.&=\frac 12 CV^2 \\\\ &=\frac 12 (150\times 10^{-6})(36)^2 \\\\ &=97.2\,\rm mJ\end{align*} As you can see, the presence of a dielectric led to an increase in the stored energy in the capacitor. This is a general rule once the dielectric is inserted into the plates while the capacitor is connected to the power supply.
Problem (3): An air-filled parallel-plate capacitor has a capacitance of $1.5\,\rm pF$. The distance between the plates is doubled, and a material with an unknown dielectric constant is inserted between them. The capacitance becomes $3.4\,\rm pF$. Find the dielectric constant of that material.
Solution: The capacitance of a parallel-plate capacitor is proportional to the plate area and inversely proportional to the plate spacing $d$. \[C=\kappa\epsilon_0 \frac{A}{d}\] The spacing of the plates is doubled, so $d_{new}=2d$. After the insertion of the dielectric, by considering the doubling of the spacing, the new capacitance is related to the old one as below \begin{align*} C_{new}&=\kappa\epsilon_0 \frac{A}{d_{new}} \\\\ &=\kappa\epsilon_0 \frac{A}{2d} \\\\ &=\frac 12 \kappa\epsilon_0\frac{A}{d} \\\\ &=\frac 12 \kappa C_0\end{align*} where $C_0$ is the air-gaped capacitor. We are given the old and new capacitance, so by substituting the numerical values into the above formula and solving for $\kappa$, we will obtain \begin{gather*} C_{new}=\frac 12 \kappa C_0 \\\\ 3.4=\frac 12 \kappa (1.5) \\\\ \Rightarrow \boxed{\kappa=4.8}\end{gather*} This one can be a nice typical dielectric problem in the AP Physics C exam.
Problem (4): An uncharged capacitor is connected to a $12-\rm V$ battery until it is fully charged. Then it is disconnected from the power supply. A slab of Polystyrene (plastic) having a dielectric constant of $2.6$ is inserted between the plates. What will finally be the voltage across the plates?
Solution: When the capacitor is fully charged it is disconnected from the battery, so there is no mechanism to change the charge stored on each plate. As a result, the charge on the plates is constant, i.e., $Q_{bef}=Q_{aft}$.
On the other hand, recall that the insertion of a dielectric with constant $\kappa$ would cause the capacitance increases by a factor of $\kappa$, $C=\kappa C_0$. Therefore, using the definition of capacitance $C=\frac QV$, we have \begin{gather*} Q_{bef}=Q_{aft} \\\\ C_0 V_0 = C V \\\\ C_0 V_0 = (\kappa C_0) V \\\\ \Rightarrow \boxed{V=\frac{V_0}{\kappa}}\end{gather*} As can be seen, the potential difference between the plates decreases by a factor of $\kappa^{-1}$. Thus, in this case, the voltage would be finally as much as \[ V=\frac{12}{2.6}=\boxed{4.6\,\rm V}\]
Problem (5): A $2500-\rm pF$ air-filled capacitor is connected to a $24\,\rm V$ battery. How much charge will flow from the battery, if a piece of Pyrex ($\kappa=5$) is inserted between the plates?
Solution: The initial charge stored on the plates is $Q_{ini}=C_0 V$
While the dielectric insulator is inserted between the space of the plates, the capacitor is connected to the battery, so the voltage across it is unchanged, $V_{ini}=V_{fin}$. The only thing that changes during this process is the capacitance and the charge stored on the plates.
Recall that, by inserting a dielectric into an air-gaped capacitor, its capacitance increases by a factor of $\kappa$ as $C_{fin}=\kappa C_{ini}$. According to the definition of the capacitance, $C=\frac{Q}{V}$, the final charge deposited on the plates increases also by a factor of $\kappa$ as $Q_{fin}=\kappa Q_{ini}$. The difference between initial and final charges gives the amount of electric charge delivered by the battery upon inserting a dielectric. \begin{align*} \Delta Q&=Q_{fin}-Q_{ini} \\\\ &=(C_{fin}-C_{ini}) V\\\\ &=(\kappa C_{ini}-C_{ini}) V\\\\ &=(\kappa-1)C_{ini}V \\\\&=(5-1)(25\times 10^{-12})(24) \\\\ &=\boxed{2.4\,\rm nC}\end{align*}
Problem (6): An air-gap parallel-plate capacitor spaced $2.4\,\rm mm$ has a capacitance of $C_0=4\,\rm pF$. (a) What is the maximum charge stored on each plate if the electric field in the space between the plates is not to exceed $25\,\times 10^4\,\rm V/m$? (b) If a dielectric of constant $\kappa=2.7$ is inserted between the plates (assuming completely fills the space), what will now be the maximum magnitude of the charge stored on each plate?
Solution: In all the dielectric problems, if the potential difference between the plates exceeds a certain value, the electric field associated with it, $\Delta V=Ed$, causes the inserted dielectric to break down.
In this situation, the dielectric that is supposed to be an insulator permits conduction through itself. Air is a dielectric with $\kappa\approx 1$. Applying a large voltage across an air-filled capacitor produces a strong electric field between the plates, which in turn damages the dielectric, making it almost a conductor.
(a) We are given the maximum electric field between the plates so that the dielectric can tolerate it without breaking. Given this, we can find the maximum voltage across the capacitor as \begin{align*} \Delta V_{max}&=E_{max}d \\\\&=(25\times 10^4)(2.4\times 10^{-3}) \\\\ &=600\,\rm V\end{align*} From the definition of the capacitance, $C=\frac{Q}{\Delta V}$, the maximum charge accumulated on each plate is found to be \begin{align*} Q_{max}&=C\Delta V_{max} \\\\ &=(4\times 10^{-12})(600) \\\\ &=2.4\,\rm nC\end{align*} This is the maximum charge that can be accumulated on each plate without damaging the dielectric (air) between them.
(b) Since the electric field has not changed, the capacitor is connected to the battery. As a result, the voltage stays constant. Recall that by inserting a dielectric material of constant $\kappa$ between the plates, the capacitance is increased by a factor $\kappa$, i.e., $C=\kappa C_0$, where $C_0$ is the capacitance of an air-filled capacitor. Using the relation $Q=CV$ and considering $V$ to be constant, the charge also increases by a factor of $\kappa$. Therefore, we have \begin{align*} Q&=\kappa Q_0 \\\\ &=(2.7)(2.4\,\rm nC) \\\\ &=6.48\,\rm nC \end{align*} This is the maximum charge accumulated on each plate when there is a dielectric material between them.
Problem (7): Two parallel metal plates of $\rm 2\,cm \times 2\,cm$ are separated by a $0.25\,\rm mm$-thick piece of Teflon.
(a) What is the capacitance?
(b) What is the maximum potential difference between the plates?
Solution: From the definition of the capacitance of a parallel-plate capacitor, we have \[C=\frac{\kappa\epsilon_0 A}{d}\] where $\kappa$ is the dielectric constant, $d$ is the spacing between the plates, and $A$ is the surface area of the plates.
(a) Between the plates is filled with a thick piece of Teflon, having the dielectric constant of $K=2.1$. The surface area of this capacitor is $A=0.02\times 0.02=4\times 10^{-4}\,\rm m^2$. Substituting the numerical values into the above formula gives us \begin{align*} C&=\frac{(2.1)(8.85\times 10^{-12})(4\times 10^{-4})}{0.25\times 10^{-3}} \\\\ &=29.73\times 10^{-12}\,\rm F\end{align*} Thus, the capacitance is $C=29.73\,\rm pF$.
(b) The maximum potential difference between the plates is related to the maximum electric field strength (or dielectric strength) by $V_{max}=E_{max}d$. By inspecting the dielectric strength of Teflon in the dielectric constant table and substituting the plates spacing, we have \begin{align*} V_{max}&=E_{max}d \\\\ &=(60\times 10^6\,\rm V/m)(0.25\times 10^{-3}\,\rm m) \\\\ &=15\,\rm kV\end{align*}
Problem (8): A paper-filled ($k=3.75$) capacitor having a separation of $1.45\,\rm mm$ has the charge $0.545\,\rm \mu C$ on each plate. Assuming the electric field between the plates is $4.5\times 10^4\,\rm V/m$, determine the capacitance and the area of each plate.
Solution: The electric field between the plates of a parallel-plate capacitor is related to the potential difference (voltage) across it by $E=\frac{\Delta V}{d}$, where $d$ is the separation of the plates.
Using the definition of capacitance, $C=\frac{Q}{\Delta V}$, and substituting $\Delta V$ from the above equation, we can find the capacitance as follows \begin{align*} C&=\frac{Q}{\Delta V} \\\\ &=\frac{Q}{Ed} \\\\ &=\frac{0.545\times 10^{-6}}{(4.5\times 10^4)(1.45\times 10^{-3})} \\\\ &=8.35\,\rm nF\end{align*} Next, applying the parallel-plate capacitance formula, $C=\kappa \epsilon_0 \frac{A}{d}$, and solving for the plate area $A$, gives us \begin{align*} A&=\frac{Cd}{\kappa \epsilon_0} \\\\ &=\frac{(8.35\times 10^{-12})(1.45\times 10^{-3})}{8.85\times 10^{-12}} \\\\ &=1.36\times 10^{-3}\,\rm m^2\end{align*} or, $A=1360\,\rm mm^2$, in terms of square millimeters. If we take this plate as a square, then it is about $37\,\rm mm$ on a side.
Problem (9): We are asked to construct a capacitor having a capacitance of $1.45\,\rm nF$ and be able to withstand a maximum voltage of $5000\,\rm V$. The dielectric to be used in this parallel-plate capacitor has a dielectric constant of $2.7$ and a dielectric strength of $24\times 10^6\,\rm V/m$. What is the minimum area of the plates of the capacitor?
Solution: The dielectric strength, $E_{max}$, gives us the maximum value of the electric field formed between the plates of a capacitor without damaging the capacitor and converting it into a conductor by flowing the charges through it.
Using the relation $V=Ed$ and the given numerical values, we can find the distance between the plates as below \begin{align*} V_{max}&=E_{max}d \\\\ 5070&=(24\times 10^6)d \\\\ \Rightarrow d&=211.25\times 10^{-6}\,\rm m\end{align*} Next, using the parallel-plate capacitor formula, $C=k\epsilon_0 \frac{A}{d}$, and solving for $A$ we have \begin{align*} A&=\frac{Cd}{\kappa \epsilon_0} \\\\ &=\frac{(1.45\times 10^{-9})(211.25\times 10^{-6})}{(2.7)(8.85\times 10^{-12})} \\\\ &=0.0129\,\rm m^2\end{align*}
Problem (10): A $0.02\,\rm mm$-thick Teflon insulator is inserted between the plates of a parallel-plate capacitor spaced by $0.05\,\rm mm$ and plates are $145\,\rm cm^2$. What is the capacitance and the maximum voltage that can be applied across the plates?
Solution: As you noticed from the question, the dielectric does not completely fill the space between the plates. We assume the capacitor is disconnected from the power supply so that the charge remains constant when the dielectric is inserted or removed.
When the insulator slab is in place between the plates, the new potential difference between the plates is the potential difference across the empty portion of the space, $V_g$, plus the potential difference across the dielectric slab, $V_s$. \[V=V_{g}+V_{s}\] Recall from potential difference problems that $\Delta V=Ed$, where $E$ is the field strength and $d$ is the straight distance between those two points.
On the other hand, we know that the electric field between two conducting charged plates is given by $E=\frac{\sigma}{\epsilon_0}$. Combining these two above expressions yields the potential difference across the gap (where there is no dielectric) \begin{align*}V_g&=E_g d_g\\\\ &=\frac{\sigma_0}{\epsilon_0}\times d_g\end{align*} where $\sigma_0=\frac{Q_0}{A}$ is the surface charge density and $Q_0$ is the initial charge stored on each plate when there is no dielectric.
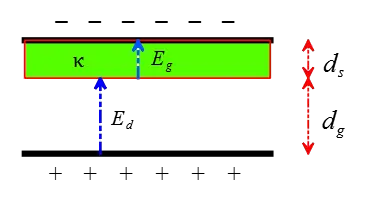
When a slab of dielectric constant $\kappa$ is inserted into the plates, the electric field inside the slab (insulator) is reduced by the factor $\kappa^{-1}$ as \[E_s=\frac{E_g}{\kappa}\] Therefore, the potential difference across the slab is found to be \begin{align*} V_s &= E_s d_s \\\\ &=\frac{E_g}{\kappa}\times d_s \end{align*} Putting together those two expressions gives us $V$ across the whole capacitor \begin{align*} V&=V_g+V_s \\\\ &=E_g d_g+\left(\frac{E_g}{\kappa}\right)d_s \\\\ &=\frac{Q}{\epsilon_0 A} \left(d_g+\frac{d_s}{\kappa}\right) \\\\ &=\frac{Q}{\epsilon_0 A}\left(\frac{\kappa d_g+d_s}{\kappa}\right)\end{align*} Hence, the potential difference $V$ was obtained in terms of the charge stored on each plate. Using the definition of capacitance, $C=\frac{Q}{V}$, the capacitance of such capacitor filled partially with a dielectric constant of thickness $d_s$ is given by \[C=C_0 \left(\frac{\kappa}{\kappa d_g+d_s}\right)\] where $C_0=\frac{\epsilon_0 A}{d}$ is the capacitance when there is no dielectric between the plates. \begin{align*} C_0&=\frac{(8.85\times 10^{-12})(145\times 10^{-4}\,\rm m^2)}{0.05\times 10^{-3}\,\rm m} \\ &=2.5\,\rm nF\end{align*} In this problem, the Teflon insulator ($\kappa=2.1$) fills as much $d_s=0.02\,\rm mm$ and the remaining space is empty (or filled with air), $d_g=0.05-0.02=0.03\,\rm mm$.
Substituting the numerical values into the above formula yields \begin{align*} C&=C_0 \left(\frac{\kappa}{\kappa d_g+d_s}\right) \\\\ &=(2.5\,\rm nF) \left(\frac{2.1}{(2.1)(0.03)+0.02}\right) \\\\ &=63.2\,\rm nF \end{align*} As can be seen, by filling some of the space between the plates with a thick dielectric of thickness $d_s$, the initial capacitance becomes much larger.
You can use this result to answer some AP Physics C questions appearing on the topic of dielectrics.
(b) In this part, we are asked to find the maximum voltage that can be applied across this specific capacitor. The dielectrics can tolerate the external electric field up to some specific limit, beyond that it loses its functions and behaves in the capacitor as if there is no dielectric in place.
The maximum electric field strength tolerated by dielectrics is called the dielectric strength (the SI units of $\rm V/m$).
For Teflon its value is $E_{max}=60\times 10^6 \,\rm V/m$. Now, applying the expression that relates electric field $E$ to potential difference $\Delta V$ over a distance $d$ as $\Delta V=Ed$, we have \begin{align*} \Delta V_{max}&=E_{max}d \\\\ &=(60\times 10^6)(0.02\times 10^{-3}) \\\\ &=1200\,\rm V\end{align*}
Problem (11): A parallel-plate capacitor has a plate area $0.05\,\rm m^2$ and spaced $0.02\,\rm mm$ apart. We want to fill the space between the plates with a piece of Quartz having a dielectric constant of $k=4.3$ as one of the configurations shown below. What is the capacitance of each configuration?
Solution: This is one of the challenging questions in the AP Physics C exam. You can use the result of this question to answer similar problems in the AP Physics C exam.
Author: Dr. Ali Nemati
Published: April 30, 2023
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
