Problem-Solving with Diverging Lenses: A Student’s Guide
Diverging lenses are a fascinating topic in optics, and working through problems is an excellent way for students to understand their properties and behavior.
Overview of diverging lenses:
A diverging lens, also known as a negative or concave lens, is characterized by being thicker at its edges than at its center.
The focal length of a diverging lens is negative, indicating that the lens spreads out light rays.
The thin lens equation gives a relationship between image distance $d_i$ and object distance $d_o$ with the focal length $f$ as below \[\frac 1f=\frac 1d_o+\frac 1d_i\] Additionally, the magnification formula also provides a relationship between image and object distances, or the heights of the image and object, as below \[M=-\frac{d_i}{d_o}=\frac{h_i}{h_o}\]
Sign conventions for diverging lenses:
(i) The focal length is always negative.
(ii) When an object is positioned in front of the lens, the object distance is considered positive.
(iii) In the case of virtual images, the image distance is assigned a negative value.
By working through the subsequent problems, you can gain a better understanding of the above concepts.
Diverging Lens Solved Problems:
Problem (1): A diverging lens with a focal length of 10 cm can form an image of an object 20 cm away from it.
(a) What is the location of the image?
(b) Is the image real or virtual?
(c) Is the image upright or inverted? and find its magnification.
(d) Draw a ray diagram and verify the above results.
Solution: The given data includes the object distance $d_o=20\,{\rm cm}$ and the focal length of a diverging lens $f=-10\,{\rm cm}$.
Remember, by convention, the focal length for a diverging lens is always considered negative.
(a) The thin-lens equation relates the image distance $d_i$, object distance $d_o$, and focal length $f$ as follows: \[\frac 1f=\frac 1d_o+\frac 1d_i\] By substituting the given information into this equation and solving for the unknown image distance, we obtain \begin{align*} \frac 1f&=\frac 1d_o+\frac 1d_i \\\\ \frac 1{-10}&=\frac{1}{20}+\frac{1}{d_i}\\\\\Rightarrow \frac{1}{d_i}&=\frac{1}{-10}-\frac{1}{20}\\\\&=\frac{-2-1}{20}=\frac{-3}{20} \end{align*} Inverting the above expression gives us $d_i=-6.6\,{\rm cm}$.
Therefore, the image is formed approximately 7 cm away from the diverging lens.
(b) According to the sign conventions for thin lenses, a negative sign for image distance indicates that the image is virtual. An image is called virtual when it is formed on the same side as the object.
(c) To determine the orientation of an image formed by a thin lens, we can use the magnification formula: \[M=-\frac{d_i}{d_o}\] A negative magnification indicates an inverted image while a positive one indicates an upright image. Substituting the image and object distances into the above formula gives \[M=-\frac{-20/3}{20}=+\frac 13\] A positive magnification was obtained, so the image is erected (upright).
Note that the absolute value of the magnification indicates the degree to which the object's size has changed. In this case, the image is as small as one-third of the object's size.
(d) To sketch a ray-tracing diagram for a diverging lens, it is sufficient to use at least three special rays:
(i) A ray parallel to the optical axis bends (refracts) toward the thicker part of the lens as if it originated from the focal point on the same side as the rays. This is known as the Parallel Ray.
(ii) A ray passing through the center of the lens is refracted without deflection. This ray is called a Central Ray.
(iii) A ray passing through the focal point (on the opposite side from where the rays are coming in) is refracted and emerges parallel to the optical axis. This ray is known as Focal Ray.
The point where all the refracted rays converge is the location of the image point.
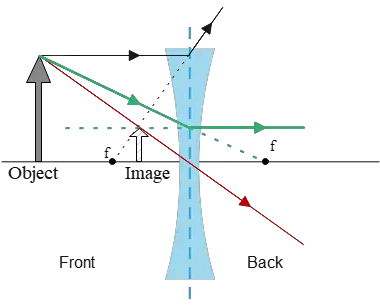
Problem (2): A diverging lens has a focal length of 20 cm. An object is placed in different places in front of it. In each case, find the image properties graphically and algebraically.
(a) The object is 40 cm in front of the lens.
(b) The object is 10 cm away from the lens.
Solution: By convention, a diverging lens has a negative focal length, so $f=-20\,{\rm cm}$.
(a) In this case, the object is located at $d_o=40\,{\rm cm}$. Using the thin lens equation, we can determine the location of the image formed by the diverging lens as follows: \begin{align*} \frac 1f&=\frac 1d_o+\frac 1d_i \\\\ \frac 1{-20}&=\frac{1}{40}+\frac{1}{d_i}\\\\\Rightarrow \frac{1}{d_i}&=\frac{1}{-20}-\frac{1}{40}\\\\&=\frac{-2-1}{40}=\frac{-3}{40} \end{align*} Thus, $d_i=-40/3\,{\rm cm}$. The negative value indicates that the image is virtual and formed on the same side as the object.
The size and orientation of the image can also be determined using the magnification formula: \[M=-\frac{d_i}{d_o}=-\frac{-40/3}{40}=+\frac 13\] The sign of magnification indicates its orientation. Here, $M$ is positive, so the image is upright.
Therefore, the image is virtual, upright, and one-third the size of the object.
(b) Now, the object sits $10\,\rm cm$ in front of the lens, so $d_o=10\,{\rm cm}$. Applying the thin-lens equation, we can find the precise location of the image as follows: \begin{align*} \frac 1f&=\frac 1d_o+\frac 1d_i \\\\ \frac 1{-20}&=\frac{1}{10}+\frac{1}{d_i}\\\\\Rightarrow \frac{1}{d_i}&=\frac{1}{-20}-\frac{1}{10}\\\\&=\frac{-2-1}{20}=\frac{-3}{20} \end{align*} The image is formed at a distance of $d_i=-20/3\,{\rm cm}$ from the lens. The negative image distance indicates that it is a virtual image.
Substituting the image and object distances into the magnification equation for thin lenses yields: \[M=-\frac{d_i}{d_o}=-\frac{-20/3}{10}=+\frac 23\] Since $M$ is positive and larger than one, the image is upright and two-thirds the object size.
The ray diagram for this configuration is as follows:
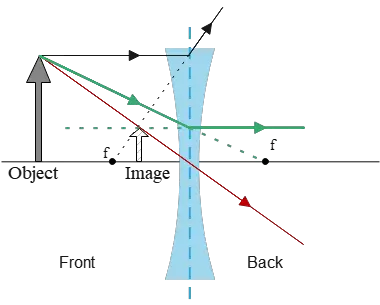
The lesson we learn from these example problems is that a diverging lens always creates a virtual, upright, and smaller in size image from an object in front of it.
Problem (3): A beam of rays strikes parallel to the optical axis of a thin lens and gets refracted as if it came from a point 30 cm from the lens. We want to use this lens to form an upright and virtual image that is one-third of the object's size. (a) What is the type of lens? (b) Where should the object be placed? (c) Where is the location of the image?
Solution: the focal point for a thin lens is defined as the point where the rays meet after refracting. If this point is where the exit rays actually converge, then that lens is a converging lens with a positive focal length (by convention).
However, if the rays appear to diverge from a point on the optical axis, then that lens is a diverging lens with a negative focal length.
(a) In this problem, we desire an upright, virtual, and small image. All these characteristics are properties of an image formed by a diverging lens.
Therefore, this is a diverging lens with a focal length of $f=-30\,{\rm cm}$.
(b) The object and image distances are unknown, but the magnification equation, $M=-\frac{d_i}{d_o}$, relates them together. By convention, we know that a positive magnification indicates an upright image, so \[M=-\frac{d_i}{d_o}=+\frac 13\] Thus, we have $d_i=-\frac 13 d_o$.
Substituting $d_i$ and $f$ into the thin-lens equation, and solving for the unknown object distance, we have \begin{align*} \frac 1f&=\frac 1d_o+\frac 1d_i \\\\ \frac 1{-30}&=\frac{1}{d_o}+\frac{1}{-1/3 d_o}\\\\ \frac{1}{-30}&=\frac{1-3}{d_o} \end{align*} Rearranging the above expression and solving for $d_o$, we have $d_o=60\,{\rm cm}$. Thus, the object should be 60 cm from the lens.
(c) Using the thin-lens equation again and solving for the unknown image distance, we get \begin{align*} \frac 1f&=\frac 1d_o+\frac 1d_i \\\\ \frac 1{-30}&=\frac{1}{60}+\frac{1}{d_i}\\\\\Rightarrow \frac{1}{d_i}&=\frac{1}{-30}-\frac{1}{60}\\\\&=\frac{-2-1}{60}\end{align*} Thus, $d_i=-20\,{\rm cm}$. The image distance is negative, as expected for a virtual image. Consequently, the image is formed on the same side as the object.
Remember, the image formed by a diverging lens is always virtual, so, by convention, $d_i<0$.
A ray-tracing diagram for this arrangement can be drawn as follows:
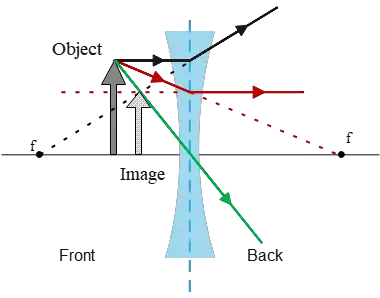
Problem (4): An object is located 20 cm to the left of an unknown lens. Its image is also formed 12 cm on the same side as the object. (a) Find the focal length of the lens. (b) Is the lens converging or diverging? (c) Determine the magnification of the lens.
Solution: The object and image distances are $d_o=20\,{\rm cm}$ and $d_i=-12\,{\rm cm}$, respectively.
A negative sign is assigned to the image distance because, as stated in the problem, the image is formed on the same side of the lens as the object. By convention, this means the image is virtual.
(a) Substituting the known values into the thin-lens equation, we have \begin{align*} \frac 1f&=\frac 1d_o+\frac 1d_i \\\\ \frac 1{f}&=\frac{1}{20}+\frac{1}{-12}\\\\&=\frac{1}{-20}-\frac{1}{-12}\\\\ \Rightarrow d_i&=-7.5\quad {\rm cm}\end{align*} Therefore, the focal length is $-7.5\,\rm cm$.
(b) Because the focal length was obtained as a negative value, the lens is a diverging or concave lens.
(c) The degree to which an object is magnified by a lens is called the magnification. Its formula is the negative of the ratio of the image distance to the object distance. Therefore, we have \[M=-\frac{d_i}{d_o}=-\frac{-12}{20}=+0.6\] A positive magnification always indicates an upright image. Consequently, the image is smaller than the object, or precisely, $0.6$ times the size of the object.
In summary, we pose a question about the diverging lens as follows:
Question: What kind of images can a diverging or concave lens form, and under what conditions can those images be formed?
Answer: From all of the problems above, we observed that
(i) A diverging lens can only form virtual images from a real object in front of it, regardless of the location of the object.
(ii) The images are smaller in size than the object.
(iii) The image is always formed within the focal length on the same side of the lens as the object.
Author: Ali Nemati
Date Published: 5/29/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
