Electric field : definition and tutorial

Electrostatic is one of the main subjects in any physics courses in high schools and colleges. The concept of the electric field, which is a topic of electrostatic, is taught in a simple, elegant, and concise way in this section with some typical problems with a descriptive answer. You can solve more problems in the ExamCenter to strengthen your understanding and get a better grade in your final or midterm exams.

Let us consider a small charged sphere of charge $q$, as shown in the figure, located at point $A$. When another particle of charge $q'$ is brought near the charge $q$ the force $\vec F$ exerts on it by $q$.

In this case, we can say that the charge $q$ has given property to its surrounding which causes a force to act on the charge $q'$.

In other words, the space around the charge $q$ has formed an electric field whose effect is perceived by the force acting on $q'$.

To find whether there is an electric field at a certain point or not, we must place a tiny positive charged particle, called test charge, at that point (why tiny? Since this charge has its own electric field and if its electric field is not small then conflict with the principal electric field of the problem).

If there is a force acting on the test charge consequently we have an electric field at that point. The electric field $\vec E$ at a certain point is defined as the ratio of the electric force $\vec F$ to the unit charge $q_0$ experienced by a charge at that point: \[\vec E=\frac{\vec F}{q_0}\]

Force is a vector quantity so the electric field is also a vector quantity. In SI units, in which the unit of force is $\rm N$ and the unit of electric charge is $\rm C$, the SI unit of the electric field is $\rm {N/C}$.

Note (1): In electrostatic literature, the location of a point charge is called the source point, and the point where the electric field or force is calculated is called the field point.

Visualization of electric field

The concept of the electric field is somewhat confusing because the electric field cannot be realized directly by the senses. To illustrate electric fields, one can use the notion of electric field lines. These lines have the following properties:

1. The field lines at each point have the same direction as the electric force acting on the positive charge at that point.
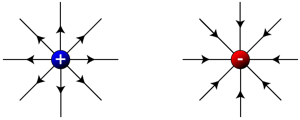
2. These lines for a positive charge always point away from the charge but towards the negative charge.
3. The field line at each point shows the direction of the electric field at that point and the electric field at each point is tangent to the field line passing through that point and is in the same direction as it. 
4. In each region where the electric field is stronger the field lines are closer and denser.
5. These lines cannot intersect with each other that is from each point in space only one field line passes. In other words, at each point of space, there is only one electric field which is the net electric field. 
6. Electric field lines start from positive charges and end on negative charges. 

 

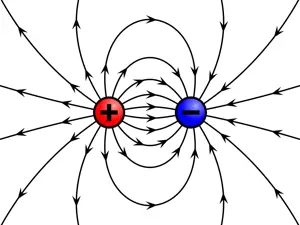
In the below the electric field around some charged objects has been shown.

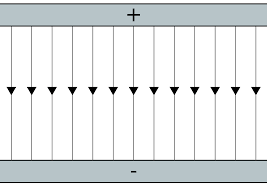
In the space between two charged parallel plates of equal magnitude and opposite sign, the electric field lines are parallel to each other. In other words, at each point within the space between the plates, the direction and magnitude of the electric field are constant. This field is called a uniform electric field.

Conceptual problems

1) Define electric force.
The force that two charged particle exerts on each other is called the electric force.

2) Define Coulomb’s law and write its relation.
The magnitude of the electric force (repulsive or attractive) between the two charges $q_1$ and $q_2$ which are apart from each other by $r$ is directly proportional to the product of $|q_1 q_2|$ and is inversely proportional to the distance squared $r^2$. One can summarize these proportionalities into the following relation called Coulomb’s law as
\[F=k\frac{|q_1q_2|}{r^2}\]

3) Define electric dipole and draw the corresponding field lines of its electric field. 
A configuration that consists of two equal but opposite charges at distance $r$ is called an electric dipole.

---

Electric field due to point charge

To obtain the electric field of a point charge $q$ at distance $r$ from it, as shown in the figure, we must place another charged particle $q_0$ at that point. According to Coulomb’s law, the force $F$ acting on the $q_0$ is \[F=\frac{1}{4\pi\epsilon_0}\frac{|q_1q_2|}{r^2}\]

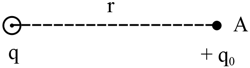
By using the definition of electric field, we have \[E=\frac{F}{q_0} \quad \Longrightarrow \quad E=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\]

This relation shows that the magnitude of the electric field due to a point charge is directly proportional to the magnitude of charge and inversely proportional to the distance squared from it. 

---

Electric field due to a collection of point charges

If we have many point charges in a region of space, at each point of space there is a unique electric field. This field is the resultant of the fields that are produced by each charge in the absence of other electric charges at that point. This prescription is called the Superposition Principle. In a few words, 
The superposition principle states that the electric field or force due to a collection of point charges on a specific charge is the vector sum of each field or force due to each individual charge that exerts on that charge. \[\vec E_{net}=\vec E_1+\vec E_2+\dots+\vec E_n \quad \text{or} \quad \vec F_{net}=\vec F_1+\vec F_2+\dots+\vec F_n\]

---

Author: Ali Nemati