Newton's Third Law of Motion: Solved Problems
In this article, you learn the concepts of Newton's third law of motion by problem-solving approach. Here, we are going to find pairs of forces appearing in Newton's third law using some worked problems.
Introduction
Consider the following everyday experiment: Imagine applying a force with a hammer to drive a nail into a wooden block. As a result, the hammer comes to a complete stop.
What forces caused the hammer's speed to be reduced to zero?
This is the question that Newton speculated on.
According to Newton's idea, the nail exerts a force of the same magnitude but in the opposite direction on the hammer, causing it to rapidly come to a complete stop upon contact.
This is the essence of Newton's third law, which states that if two objects 1 and 2 interact, the force $\vec{F}_{12}$ that object 1 exerts on object 2 is equal in magnitude but opposite in direction to the force $\vec{F}_{21}$ that object 2 exerts on object 1. \[\vec{F}_{12}=-\vec{F}_{21}\] One of the most important consequences of this law is that the forces cannot exist in isolation and always occur in pairs.
Solved Problems:
Problem (1): A box stands on a table. Identify all action-reaction forces between the box and the table.
Solution: If object 1 exerts a force of $\vec{F}_{12}$ on object 2, object 2 also exerts a force $\vec{F}_{21}$ on object 1. This force is equal in magnitude and opposite in direction and can be written as $\vec{F}_{12}=-\vec{F}_{21}$. This simple relation represents Newton's third law of motion.
In this definition, one of the forces, regardless of which one, is referred to as the action force, while the other force is known as the reaction force.
When dealing with problems involving Newton's third law, the main objective is to identify pairs of forces that comply with this law.
The box sitting on a chair does not fall through due to its weight $\vec{w}$. An upward force called the normal force $\vec{n}$ is exerted on the box to balance out the downward weight force and keep the box at rest on the table. These two forces are actual external forces.
We consider this normal force as the action force. The reaction to $\vec{n}$ is the force exerted by the box on the table, denoted as $\vec{n}'$. This reaction force has equal magnitude but opposite direction to $\vec{n}$.
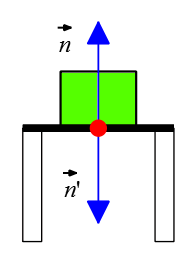
Thus, we can express this pair of forces as $\vec{n}=-\vec{n}'$. Since these forces are exerted on two different objects, they can be considered an action-reaction pair according to Newton's third law.
Problem (2): Identify the action-reaction force pair in each of the following situations:
(a) An apple falls freely.
(b) A hammer hits a nail.
(c) The blades of a helicopter push air downward.
Solution: Newton's third law states that when two objects interact, the force that object 1 applies on object 2, called $\vec{F}_{12}$ is equal in magnitude but in the opposite direction to the force that object 2 exerts on object 1, i.e., $\vec{F}_{21}$. \[\vec{F}_{12}=-\vec{F}_{21}\] In all Newton's third law problems, first of all, identify the system under study.
(a) Here, the apple and the Earth create our system. The Earth applies a downward force on the apple, known as weight $\vec{w}$, and correspondingly, the apple exerts a force on the Earth by $\vec{w}'$. These two are third law force pairs. \[\vec{w}=-\vec{w}'\]
(b) In this case, our system is hammer-nail, two different interacting bodies. The force exerted by the hammer on the nail $\vec{F}_{hn}$ is equal in magnitude but in the opposite direction to the force exerted by the nail on the hammer, $\vec{F}_{nh}$. \[\vec{F}_{hn}=-\vec{F}_{hn}\]
(c) The blades and air form a system as a combined two interacting objects. In this case, the blades exert a force downward on the air and conversely, the air also exerts a force upward on the blades. These two forces act on different objects, not the same object, so it can be considered as Newton's third law pair force.
Problem (3): A car is skidding to a complete stop on a horizontal road. First, identify all action-reaction pairs of forces, then show them on a free-body diagram.
Solution: The car slows down and eventually comes to a complete stop, experiencing deceleration. According to Newton's third law, action-reaction pairs of forces act between two interacting objects. In this case, the car and the road (Earth) form our system. The gravitational force on the car due to Earth is represented by $\vec{w}$, while the reaction force exerted by the car on Earth is represented by $\vec{w}'$. Therefore, these two forces act on different objects. \[\vec{w}=-\vec{w}'\] When the car is in contact with the road, an upward force is exerted by the road's surface on the car, known as the normal force ($\vec{n}$). Conversely, the car also applies a downward force on the road with the same magnitude but in the opposite direction ($-\vec{n}'$). These two forces form another pair of action-reaction forces according to Newton's third law.
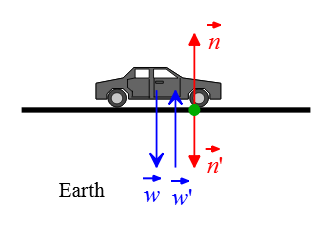
Problem (4): A girl exerts a force of 40 N upward to hold a box. Identify the reaction force by determining (a) its magnitude and direction, (b) on what object it is exerted, and (c) by what object it is exerted.
Solution: Here, three objects are interacting, the girl, the box, and the Earth. The Earth exerts a gravitational force $\vec{F}_g$ on the box. The reaction to this force is the force exerted by the box on the Earth, $\vec{F}'_g$. These two forces are acting on two different objects and are equal in magnitude and opposite in direction, so they form an action-reaction pair force. \[\vec{F}_g=-\vec{F}'_g\] On the other hand, the box is held by the girl. The girl exerts an upward force to hold it up and the reaction to this force is the force exerted by the box downward on the girl's hand.
Problem (5): A girl stands on a spring scale while riding in an elevator accelerating at $2\,\rm m/s^2$ upward. How does Newton's third law apply to find the scale reading?
Solution: The scale reads the value of the downward force that the girl exerts on the spring scale. By Newton's third law, the reaction to this force is the upward force exerted by the scale on the woman, known as the normal force $\vec{n}$. These two forces are depicted in the following figure.
Applying Newton's second law gives us the magnitude of the apparent weight that the girl feels while riding in a moving elevator. To see how to solve such elevator problems, read this.
Problem (6): A box is pushing on a rough horizontal surface at constant velocity with a force of $\vec{F}$. The friction is also applied by $-\vec{F}$. Are the pushing force and friction the action-reaction pair of forces?
Solution: It is important to remember that according to Newton's third law, force pairs appear between two interacting bodies. In this scenario, three objects are interacting: the person applying a push on the box, the box itself, and the surface over which the box is moving.
In the person-box system, an external force $\vec{F}$ is applied to the box by the person. As a reaction to this force, the box exerts an equal and opposite force $-\vec{F}$ on the person.
In the box-surface (Earth) system, friction $-\vec{F}$ is exerted on the box by the rough surface. Conversely, as a reaction to this frictional force, an equal and opposite force $\vec{F}$ is exerted by the box on the surface.
As you can see, both the push force and friction are applied separately to the same object (the box). Therefore, they cannot be considered as third law pair forces.
Problem (7): A person is standing motionless on the level ground.
(a) Identify all forces acting on the person. (Hewit 49, p.120)
(b) Are these forces equal in magnitude and opposite?
(c) Do these forces make an action-reaction force pair? Why or why not?
(d) Determine all other pairs of forces not shown here.
Solution: (a) The Earth pulls down the person by the weight force, $\vec{w}$ and the surface prevents the person from sinking into the Earth by the upward support force, called normal force $\vec{n}$.
(b) The person is motionless on the level ground, so by the second law, the net force on it must be zero which yields \begin{gather*} F_{net}=ma\\ \vec{w}+\vec{n}=0 \\ \Rightarrow \boxed{\vec{w}=-\vec{n}}\end{gather*} This expression tells us that these two above forces are equal in magnitude and opposite in direction.
(c) Every two equal and opposite forces do not constitute an action-reaction pair of forces. Newton's third law states that these forces must be applied to two different objects.
In this problem, the Earth exerts a downward force (weight) on the person, and the person also exerts an upward force on the Earth with the same magnitude.
Additionally, the Earth's surface applies an upward force (normal force) on the person, and the person exerts an equal and opposite force on the Earth.
As you can see, both weight and normal forces are exerted separately between the Earth and the person and do not interact with each other. Therefore, these forces do not form a pair according to Newton's third law.
(d) In the previous section, we mentioned that the weight and normal forces are actual external forces and not paired forces. In this context, the downward weight acts as an action, with its reaction being the force that pulls the Earth towards the person. Similarly, the upward normal force acts as an action, with its reaction being the downward force exerted by the person on the surface.
Problem (8): An astronaut performing a spacewalk with a combined mass of 165 kg applies a force of 280 N to a satellite that is freely floating in space and has a mass of 850 kg. Determine the magnitude and direction of the reaction force exerted by the satellite on the astronaut. Additionally, calculate the accelerations experienced by both the astronaut and the satellite.
Solution: The satellite and the astronaut are two distinct objects that interact with each other by the forces that make the action-reaction pair force, according to Newton's third law of motion.
(a) The astronaut applies a force $\vec{F}_{as}$ to the satellite and, by Newton's third law, the satellite also exerts an equal force in the opposite direction on the astronaut as $-\vec{F}_{sa}$. Thus, the satellite exerts a $280\,\rm N$ force on the astronaut in the negative $x$-direction or in vector notation as \[\vec{F}_{sa}=-280\,\rm N\]
(b) The second law gives us the acceleration of an object when a force $F$ is applied to it as $\vec{a}=\frac{\vec{F}}{m}$. Therefore, the astronaut's acceleration is \[a=\frac{-280}{165}=-1.70\,\rm m/s^2\] and for the satellite can be found as \[a=\frac{280}{850}=0.33\,\rm m/s^2\] The negative indicates the direction of the acceleration, which is toward the negative $x$-axis.
Author: Dr. Ali Nemati
Published: August 27, 2023
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
