Ohm's Law Practice Problems With Solutions for High School
Excel in solving any Ohm’s law problems with this comprehensive guide. It’s your ultimate toolkit for tackling homework and acing the AP Physics exam.
If you are a teacher looking for a resource to assess your students, download this Ohm’s law worksheet.
Ohm's Law Practice Problems:
Problem (1): An electronic device has a resistance of 20 ohms, and a current of 15 A passes through it. What is the voltage across the device?
Solution: Resistance, current, and voltage are related together by Ohm's law as $V=IR$. Thus, the voltage of the device is given by \begin{align*}V&=IR\\&=15\times 20\\&=300\quad {\rm V}\end{align*}
Problem (2): A $3-{\rm V}$ potential difference is applied across a $6\,{\rm \Omega}$ resistor. What is the current that flows into the resistor?
Solution: Ohm's law states the potential difference across a resistor is resistance times current, so we get \begin{align*} I&=\frac VR\\&=\frac {3}{6}\\&=0.5\quad {\rm A}\end{align*}
Problem (3): An electric device is connected to a $120-\rm V$ outlet and draws $6\,\rm A$ of current. How much heat will this device produce in $3$ minutes?
Solution: To solve this simple question, we must combine three fundamental equations as follows: \begin{gather*} \text{Ohm's law}: \, I=\frac{V}{R}\\\\ \text{Power}: P=\frac{E}{t} \\\\ \text{Electric power}: P=V\times I \end{gather*} where $E$ is energy. Recall from heat problems that heat is energy. Combining these equations yields \begin{align*} E&=Pt \\\\ &=VIt\\\\ &=(120)(6)(3\times 60\,\rm s) \\\\ &=129600\,\rm J\end{align*} or in scientific notation as \[E=1.29\times 10^5\,\rm J\]
Problem (4): In the circuit shown below, how much current does the ammeter show?
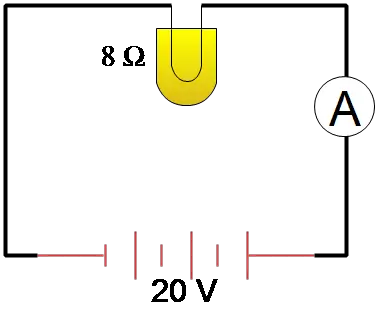
Solution: A lightbulb is an electronic component with high resistance. In the figure, the voltage across it is the same as that across a battery of $V=20\,{\rm V}$. The current that passes through it relates to the resistance and voltage drop using Ohm's law. \begin{align*} I&=\frac VR\\&=\frac{20}{8}\\&=1.25\quad {\rm A}\end{align*}
Your donation will help us keep our physics lessons accessible to students around the world. Thank you for your support.
Problem (5): In a circuit, a $10\,{\rm \Omega}$ resistor is removed and replaced by a $20\,{\rm \Omega}$ resistor. What happens to the current in the circuit?
Solution: Since nothing is said about the voltage drop across the circuit, we assume it is constant, say $V=120\,{\rm V}$. Therefore, using Ohm's law formula, $I=\frac VR$, current $I=\frac{120}{10}=12\,{\rm A}$ flows through the $10\,{\rm \Omega}$ resistor, and $I=\frac{120}{20}=6\,{\rm A}$ through the $20\,{\rm \Omega}$ resistor.
We can see that for the same voltage, doubling the resistances results in decreasing, or more precisely, halving, the currents. This is a clear demonstration of Ohm’s law.
Question: A circuit consists of a battery and a resistor. The resistor dissipates $2\,\rm W$. Now the resistor is replaced with one that has twice the resistance of the original. What power does the new resistor dissipate?
Solution: The power dissipated (or consumed) by a resistor is determined by one of the following formulas: \[P=V\times I=\frac{V^2}{R}=RI^2\] where $V$ is the potential drop across the resistor.
Ohm's law tells us that the current through a resistor is inversely proportional to its resistance, i.e., $I\propto \frac 1R$.
In this problem, the new resistor has twice the resistance of the original resistor, i.e., $R'=2R$ whereas it is connected across the same battery, $V'=V$. Thus, the current flowing through this new resistor is related to the old one as below: \begin{align*} \frac{i'}{i}&=\frac{R}{R'} \\\\ &=\frac{R}{2R} \\\\ \Rightarrow i'&=\frac 12 i\end{align*} Given the current in the replaced resistor, substitute it into one of the above power formulas, say $P'=V'i'$. \begin{align*} P'&=V'i' \\\\ &=V(\frac 12 i) \\\\ &=\frac 12 \underbrace{Vi}_{P} \\\\ &=\frac 12 \times 2 \\\\ \Rightarrow \quad P'&=\boxed{1\,\rm W} \end{align*} Therefore, the new resistor would dissipate $1\,\rm W$ of electric power.
Question: A hair dryer is plugged into a $240\,\rm V$ outlet and draws a current of $3.6\,\rm A$.
(a) If the voltage drops by $25\%$ and nothing else changes, how much will the current be?
(b) Assuming that the resistance of the device was reduced by $25\%$, what current would be drawn at $240\,\rm V$?
Solution: This type of Ohm's law question typically appears in AP Physics classes.
(a) We are told that the voltage is reduced by $25\%$ of the original voltage, meaning that \[V_2=V_1-(0.25)V_1=0.75V_1\] In addition, it is assumed that the resistance of the device has not changed, i.e., $R_2=R_1$. Applying Ohm's law formula on both sides of this relation and solving for the unknown current $I_2$ gives us \begin{align*} R_2&=R_1 \\\\ \frac{V_2}{I_2}&=\frac{V_1}{I_1} \\\\ \Rightarrow I_2&=I_1\left(\frac{V_2}{V_1}\right) \\\\ &=(3.6)\left(\frac{0.75V_1}{V_1}\right) \\\\ &=\boxed{2.7\,\rm A} \end{align*} With a $25\%$ reduction in the original voltage, the current drawn by the device is also reduced by as much as $2.7\,\rm A$.
(b) Now, the resistance varies and reduces by $25\%$ of the original resistance, i.e., \[R_2=R_1-0.25R_1=0.75 R_1\] The voltage across the device is held constant, i.e., $V_2=V_1$. As above, applying Ohm's law formula gives us \begin{align*} V_2&=V_1 \\\\ I_2R_2&=I_1 R_1 \\\\ \Rightarrow I_2&=I_1 \left(\frac{R_1}{R_2}\right) \\\\&=(3.6)\left(\frac{R_1}{0.75R_1}\right) \\\\ &=\boxed{4.8\,\rm A} \end{align*} The current will be $4.8\,\rm A$ if the resistance is reduced by $25\%$ at $240\,\rm V$.
Ohm's Law: Conceptual Questions
Here are some simple conceptual questions about Ohm's Law.
Question: When you double the voltage across a conducting wire, you observe that the current increases by a factor of $4$. What can you conclude about this experiment?
Solution: The resistance of a conducting wire is defined as the ratio of the voltage drop across it to the current that passes through it, $R=\frac{\Delta V}{I}$. This relationship is commonly referred to as Ohm's law.
For ohmic materials, the resistance, $R$, is always constant and does not change, either by changing voltage or current.
In this question, the voltage was doubled $V'=2V$ and it was observed that the current was quadrupled $I'=4I$. Applying Ohm's law gives \begin{align*} R' &=\frac{V'}{I'} \\\\ &=\frac{2V}{4I} \\\\ &=\left(\frac 12\right) \frac VI \\\\ \Rightarrow R' &=\frac 12 R \end{align*} As you can see, the new resistance is halved, which contradicts the assumption that for an ohmic material, the $R$ value should be constant.
Therefore, we conclude that this conducting wire does not obey Ohm's law.
This is a clear demonstration of the limitations of Ohm’s law and its applicability to real-world materials.
It’s important to remember that Ohm’s law is an idealized model and may not hold true under all circumstances.
Question: All lamps are identical in the circuit shown. If the switch is closed, what happens to the brightness of bulb A?

Solution: In a parallel circuit, each lamp has its own independent circuit to the battery. Therefore, if one lamp fails (i.e., its filament breaks) or is added to the circuit by an on/off switch, it will not affect the other lamp.
The brightness of the remaining lamp will stay the same because the same amount of current will continue to flow through it.
This is one of the advantages of parallel circuits in practical applications like home lighting. Even if one light goes out, the others will continue to shine brightly.
Question: In the circuit illustrated, rank each branch of the circuits, from greatest to least, according to
(a) The voltage drop across each
(b) The current through each
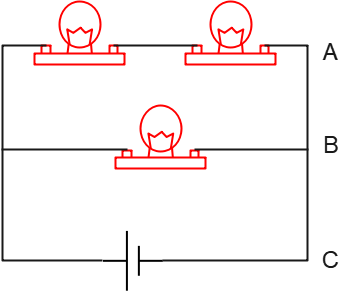
Solution: We want to solve this question without any mathematical calculation.
(a) All three branches are in parallel with each other, so the potential drop of each is the same and equal to the voltage of the battery. \[V_C=V_A=V_B\]
(b) Assuming an ideal battery (without internal resistance), the top branch has two resistors, the middle branch has one, and the third branch has none.
The top branch is therefore more resistant than the other branches. On the other hand, they are all the same voltage.
Ohm's law states that any branch with more resistance draws less current as a result. As a result, we have \[I_C>I_B>I_A\]
Question: In the circuit illustrated, compare the brightness of each identical bulb.
(a) Which bulbs draw the most current?
(b) What will happen if lamp $A$ is burned out? or if lamp $C$ is unscrewed?
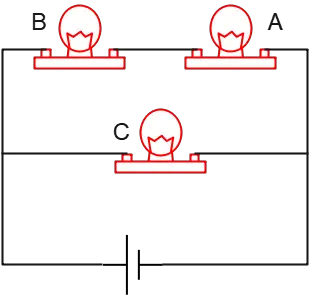
Solution: The light bulb's brightness intensity is determined by the wattage using (power) of that bulb. The power, also, is found using one of the following formulas \[P=VI=\frac{V^2}{R}=RI^2\] The more power the bulb dissipates, the brighter it shines.
The terminals of bulb C are connected directly to the battery, so the voltage across bulb C is the same as that of the battery.
The three bulbs are identical, so the equivalent resistance
This circuit is made up of two parallel branches. There is more resistance in the upper branch of the circuit, so according to Ohm's law $I=\frac VR$, less current passes through this branch than in the lower branch, including one resistor (bulb). \[i_{AB}<i_C\] Therefore, bulb C is the brightest because it draws more current than the top bulbs.
(b) Both bulbs $A$ and $B$ are connected in series and share the same current. Failing a bulb connected in series to others, say $A$, stops flowing the current through that branch. Thus, both top bulbs no longer give light and are turned off.
The lamp $C$ is connected in parallel with the other two bulbs and unscrewing it does not affect the others on the top branch, because it is connected directly to the terminals of the battery. Therefore, It glows as before.
Question: We have two identical light bulbs and a battery.
(a) Will they shine brighter if they are connected in series or in parallel?
(b) In which case does the battery drain faster?
Solution: Either the amount of current that flows through a lightbulb or the amount of power that it dissipates determines how bright it is.
(a) When two bulbs are connected in series to an ideal battery, they share a common current determined by the following Ohm's law formula: \[I_1=I_2=\frac{V}{R_1+R_2}\] Setting $R_1=R_2=R$ gets \[I_1=I_2=\frac{V}{2R}\] In the case of a parallel combination of two resistors, the equivalent resistance is given by the following well-known formula: \[R_{eq}=\frac{R_1 R_2}{R_1+R_2}\] On the other hand, Ohm's law formula, $I=\frac{V}{R}$, gives us the current that passes through the battery. \begin{align*} I_{tot}&=\frac{V}{R_{eq}} \\\\ &=(R_1+R_2)\,\frac{V}{R_1 R_2}\end{align*} Again, for two identical bulbs (or resistors), we have \[I_{tot}=2\times \frac{V}{R}\] This is the current through each parallel branch. As a result, you can see that, if the bulbs are identical, the current in the parallel case is four times that in the series combination.
(b) The amount of power dissipation by a battery determines how quickly it drains, which is given by the following power formula \[P_{diss}=VI_{tot}\] where $V$ is the voltage across the battery.
As you can see above, connecting two identical bulbs in parallel will draw more current from the battery than connecting them in series. Consequently, the more current is drawn from the battery, the more power is dissipated by it. \begin{gather*} I_{parallel} > I_{series} \\\\ P_{parallel} > P_{series} \end{gather*}
Question: In the following circuits shown, all bulbs are identical. In each circuit, a voltmeter is connected across a single bulb to measure the voltage difference across it. Rank the voltage readings from greatest to least.
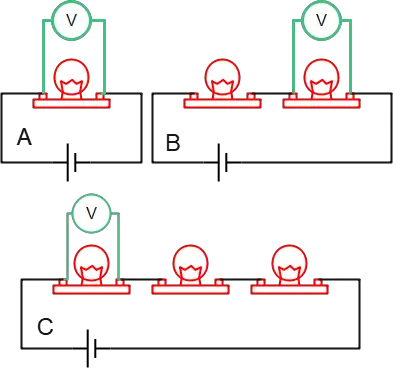
Solution: The voltage drop across each bulb is found using Ohm's law: $\Delta V=I\times R$. Assume that every lightbulb has a resistance of $R$. The only thing left to do is determine the current flowing through each bulb.
Keep in mind that in each circuit, the voltmeter is connected in parallel to the lightbulb.
For circuit (A), the voltage drop across the only bulb of the circuit is simply determined as \[\Delta V=\Delta V_A=I_A\times R\] where $I_A$ is the current through the bulb, which in this case, is also the same current as in the battery. $\Delta V$ is also the voltage difference across the battery.
In the case of B, the two identical bulbs are connected in series. Therefore, according to the rules of series combination, the same current flows through each bulb, and the voltage drop in each bulb adds up to the voltage of the battery.
The equivalent resistance of this combination is $R_{eq}=R+R=2R$, and the total current through the battery (which is the same current as each bulb) is \begin{align*} I&=\frac{\Delta V}{2R} \\\\ &=\frac 12 \frac{\Delta V}{R} \\\\ &=\frac 12 I_A\end{align*} Hence, the voltage drop across the bulb shown is \[\Delta V_B=I_B\times R = \boxed{\frac 12 I_A \times R}\] In the third circuit, only another identical bulb is added to the circuit. Thus, all calculations are similar to the second circuit, but with only a slight change. \begin{gather*} R_{eq}=R+R+R=3R \\\\ I=\frac{\Delta V}{R_{eq}}=\frac{\Delta V}{3R}=\frac 13 I_A \\\\ \Delta V_C=I_C \times R \\\\ \Delta V_C=\frac 13 I_A R \\\\ \Rightarrow \boxed{\Delta V_C=\frac 13 \Delta V_A} \end{gather*} Consequently, the rank of the voltage drop across each bulb from greatest to least is as follows \[\Delta V_A>\Delta V_B > \Delta V_C\]
Question: If the voltage across a circuit increases by five times, then what would the current through the circuit be?
Solution: Assuming the circuit is made of a material that obeys Ohm's law, a change in voltage will change the current so that the ratio of $\frac{\Delta V}{I}$ becomes constant.
Therefore, the current also increases five times to maintain the resistance of the circuit unchanged.
Question: In a certain electric circuit including a cell, connecting wires, and a filament lightbulb, which of the following would cause the lightbulb to shine less brightly?
(a) Decrease or increase the resistance of the circuit.
(b) Increase or decrease the voltage of the battery.
Solution: As long as the current through the filament lightbulb is small, we can assume Ohm's law will be obeyed.
(a) If a lightbulb shines less brightly, it means less current is passing through the filament (resistance). According to Ohm's law, the current is inversely proportional to the resistance. Therefore, an increase in the resistance will cause a decrease in the current through the filament, resulting in a dimmer lightbulb.
(b) The current through the filament is related to the voltage across it by $I=\frac{\Delta V}{R}$. Assuming the resistance of the lightbulb remains constant, the current is proportional to the voltage drop. Thus, an increase in voltage causes an increase in the current through the resistor, making the lightbulb shine brighter.
Question: A $12-\rm V$ battery is connected across a lightbulb with variable resistance. As the resistance increases, what happens to each of the following quantities?
(a) The current through the lightbulb.
(b) The voltage across the lightbulb.
(c) The power consumed by the lightbulb.
Solution: We have a circuit with a fixed-voltage battery of $12\,\rm V$, and a lightbulb (resistor) with variable resistance. We assume that the filament of the lightbulb is made up of a material that obeys Ohm's law.
(a) According to Ohm's law, the current through a resistance is $I=\frac{\Delta V}{R}$. The voltage is assumed to be fixed, and the only alteration is due to the increases in the resistance. Thus, increasing the resistance decreases the current through the lightbulb filament.
(b) The voltage across the bulb is held constant by a battery and does not change with a change in circuit resistance.
(c) One of the following formulas can be used to calculate the power consumed by resistance in a circuit: \[P=I\Delta V=\frac{\Delta V^2}{R}=RI^2\] If we pick out the first formula, $P=I\Delta V$, as you can see in part (a), an increase in the resistance leads to a decrease in the current, and so does power.
Ohm's Law: Homework Problems
The following are some homework questions appearing for Ohm's law are provided and answered.
Problem (6): In the following circuits, find the unknowns.
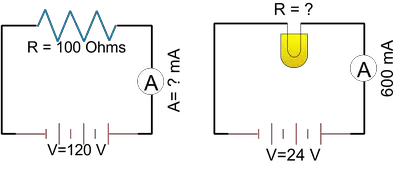
Solution: In each of the circuits, use Ohm's law $V=IR$ and solve for the unknown. In the left circuit, the current through the resistor is asked for in milliamps. Thus, \begin{align*} I&=\frac VR\\\\&=\frac{120}{100}\\\\&=1.2\quad {\rm A}\end{align*} To convert it to milliamperes, multiply it by $1000$, so we get $I=1200\,{\rm mA}$.
In the right circuit, the resistance of the light bulb is unknown. As a result, \begin{align*} R&=\frac VI\\&=\frac {24}{600\times 10^{-3}} \\\\&=40\quad {\rm \Omega}\end{align*}
Problem (7): In a circuit, the potential drop across the $10\,\rm k\Omega$-resistor is $100\,\rm V$. What is the current through the resistor?
Solution: Substitute all known numerical values into Ohm's law equation, $V=IR$. \begin{align*} I&=\frac VR\\\\&=\frac{100\,{\rm V}}{10000\,{\rm \Omega}}\\\\&=0.01\quad {\rm A}\end{align*}
Problem (8): The voltage-current curve for an ohmic conductor is plotted as shown in the figure below. What is the resistance of resistors 1 and 2?
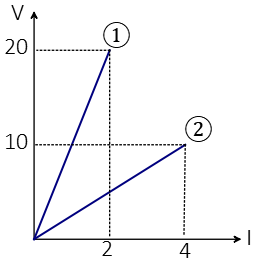
Solution: Ohm's law tells us that resistance is the slope of the voltage vs. current curve $R =\frac{\Delta V}{I}$. Recall that the slope $m$ of a straight line between two points $A(x_1,y_1)$ and $B(x_2,y_2)$ is determined as \[m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}\] Thus, the slope of the voltage-current curve, which is the resistance, is obtained as below:
The points $A(0,0)$ and $B(2,20)$ are on the line (1):\[R_1=\frac{20-0}{2-0}=10\quad{\rm \Omega}\]
The points $A(0,0)$ and $B(4,10)$ are on the line (2):\[R_2=\frac{10-0}{4-0}=2.5\quad{\rm \Omega}\]
Problem (9): Reverse the position of the potential drop across a conductor and the current passing through it in the previous problem, so that the current-voltage curve is obtained. Now, find the resistance of resistors $1$ and $2$.
Solution: if we rearrange Ohm's law as $I=\frac{1}{R}\Delta V$, we can see that the slope of the current-voltage curve, in this case, gives the inverse of the resistance. Therefore, as in the previous problem,
the slope of the line (1) is \[\frac{1}{R_1}=\frac{20-0}{2-0}=10\] which gets the $R_1=0.1\,{\rm \Omega}$ and slope of the line (2) is \[\frac{1}{R_2}=\frac{10-0}{4-0}=2.5\] which gives $R_2=0.4\,{\rm \Omega}$.
Problem (10): A student conducts an experiment and measures the current and voltage across two unknown resistors. Then she plots her findings in current-voltage coordinates, as shown in the figure. What can be said about resistors A and B?

Solution: Ohmic materials are the ones that have constant resistance over a wide range of applied voltages. In other words, in an ohmic conductor, the ratio of the voltage across it to the current through it, which is defined as resistance, is always constant.
Thus, ohmic materials have a linear current-voltage relationship, and their curve passes through the origin. In contrast, materials with a resistance that changes with a potential drop or current are called non-ohmic.
The curve of a non-ohmic material is not linear. Examples of non-ohmic materials that violate Ohm's law are diodes and transistors.
With these explanations, as the curve of (A) is linear and passes through the origin, it is an ohmic conductor whose slope gives the reciprocal of the resistance. As in the previous problem, its resistance is calculated as $R_A=5\,{\rm \Omega}$.
The resistor (B) has a nonlinear relationship between the voltage across it and the current, so it is a non-ohmic conductor with variable resistance.
Problem (11): A subwoofer needs a household voltage of 110 V to push a current of 5.5 A through its coil. What is the resistance of the subwoofer?
Solution: Known are the voltage difference $V=110\,{\rm V}$ and current $I=5.5\,{\rm A}$. Ohm's law relates them as below: \begin{align*} R&=\frac VI \\ \\ &=\frac{110}{5.5} \\ \\ &=20\quad {\rm \Omega}\end{align*}
Problem (12): How much current is drawn from a circuit with a resistor of 1000 ohms if powered by a battery with 1.5 volts?
Solution: Resistance $R=1000\,{\rm \Omega}$ and voltage $V=1.5\,{\rm V}$ are known, so we have \begin{align*}I&=\frac VR\\\\&= \frac{1.5}{1000} \\\\&= 1.5\quad {\rm mA}\end{align*}
Problem (13): An electric heater has a coiled metal wire that draws a current of 100 A. The resistance of the wire is 1.1 ohms. Calculate the voltage that must be established for it.
Solution: Current $I=100\,{\rm A}$ and resistance $R=1.1\,{\rm \Omega}$ are related as \begin{align*} V&=IR\\&=100\times 1.1\\&=110\quad {\rm V}\end{align*}
Problem (14): The maximum current that passes through a light bulb with a resistance of 5 ohms is 10 A. How much voltage must be applied across its ends before the bulb will break?
Solution: The maximum voltage can be found using Ohm's law as below: \begin{align*} V&=IR \\ &= 10\times 5\\&=50 \quad {\rm V}\end{align*} If a voltage higher than this value is applied to the circuit, the lamp will burn out.
Problem (15): In a circuit, we replace the previous 1.5-volt battery with a 3-volt new one. What happens to this circuit?
Solution: Ohm's law tells us that when more voltage is established across a circuit, then a higher current will flow through the resistors in that circuit, like electric heaters, light bulbs, and so on.
More current can cause damage or failure to household appliances. For example, a light bulb with a resistance of $R=1.5\,{\rm \Omega}$ draws a current of $I=\frac{1.5}{1.5}=1\,{\rm A}$ with a $1.5$ volt battery and a current of $I=\frac{3}{1.5}=2\,{\rm A}$ with a replacement one. In these cases, the light bulb will most likely burn out.
Summary:
Ohm's law tells us that the current in a circuit is directly proportional to the voltage drop across it and inversely proportional to the circuit's resistance: \[\text{Current}=\frac{\text{voltage}}{\text{resistance}}\] or \[I=\frac{V}{R}\]
Author: Dr. Ali Nemati
Page Created: 12/6/2020
Last Update: May 29, 2023
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
