- Home
- Physics Problems
- Problems
Solved Problems
A pendulum has a period $14.4\, {\rm s}$ on earth. This same pendulum is taken to the mars and set into oscillation. Its period on mars is $23.1\, {\rm s}$. what is the surface gravity on mars?
The period of a pendulum with length $L$ is $T=2\pi\sqrt{\frac{L}{g}}$ where $g$ is the gravitational acceleration or surface gravity. Therefore their ratio is \[\frac{T_E}{T_M}=\frac{{2\pi}/{\sqrt{\frac{L}{g_E}}}}{{2\pi}/{\sqrt{\frac{L}{g_M}}}}=\sqrt{\frac{g_M}{g_E}}\] Solving the above relation for $g_M$, we will have \begin{align*}g_M&=g_E\,{\left(\frac{T_E}{T_M}\right)}^2\\\\ &=(9.8){\left(\frac{14.1}{23.1}\right)}^2\\\\&=3.81\quad {\rm m/s^2}\end{align*} Refer to the following to learn more about simple pendulum:
Problems on simple pendulum
A mass is oscillating on a spring with a period of ${\rm 4.60\ s}$. At $t =0\, {\rm s}$ the mass has zero speed and is at $x=8.30\,{\rm cm}$. What is its speed at $t=2.50\,{\rm s}$?
The general equation for a mass undergo a simple harmonic motion (SHO) is as
\[x=A{\cos (\omega t+\alpha)\ }\]
Where $A,\ \omega$ and $\alpha$ are constants. $A$is called the amplitude of the oscillation which is the maximum displacement from equilibrium. The argument of the cosine function, $\omega t+\alpha$, is called the phase of the motion and the $a$ also is called the phase constant, which is equal to the phase at $t=0$. The velocity of the mass in the SHO is obtained by the first derivative of the $x$ with respect to time
\[v_x=\frac{dx}{dt}=-A\omega\,{\sin (\omega t+\alpha)\ }\]
In these equations $\omega=2\pi/T$ is the angular frequency of oscillating system, where $T$ is the period of the system.
From the given information, find the phase of the motion as follows
\[v_x\left(t=0\right)=A\omega\,{\sin \left(\omega\left(0\right)+\alpha\right)\ }=0\Rightarrow A\omega\,{\sin a\ }=0\]
\[\Rightarrow \ A\omega=0\ or\ \ {\sin \alpha\ }=0\]
The first term cannot be zero, since this is the multiplication of two constant of the motion. The second term states that $\alpha=0,\frac{\pi}{2},\dots $. So we choose $\alpha=0$. Now by setting $t=0$ in the position equation, we can find the amplitude of the motion
\[x\left(t=0\right)=A\,{\cos (\omega\left(0\right)+0)\ }=8.30\Rightarrow A=8.30\ {\rm cm}\]
With these information, the full equation of the velocity of the motion is
\[v_x=-(8.30)\omega\,{\sin \omega t\ }\]
By substituting $\omega=2\pi/4.6$ and $t=2.50\ {\rm s}$ into above, we obtain the velocity at the desired time.
\[v_x=-8.30\times \frac{2\pi}{4.6}{\sin \left(\frac{2\pi}{4.6}\left(2.5\right)\right)\ }=3.06\ {\rm m/s}\]
The position of an air-track cart that is oscillating on a spring is given by $x=\left(12.4\ {\rm cm}\right)\,{\cos (6.35\ {{\rm s}}^{{\rm -}{\rm 1}})t\ }$. At what value of $t$ after $t=0$ is the car first located at $x=8.47\, {\rm cm}$?
By comparing the $x$ position equation of the cart with the standard equation of an oscillating system, we can find the amplitude and angular frequency of the cart.
\[x=A{\cos (\omega t+\alpha)\ }\ ,\ \ x=\left(12.4\ {\rm cm}\right){\cos (6.35\ {{\rm s}}^{{\rm -}{\rm 1}})t\ }\]
\[\Rightarrow A=12.4\ {\rm cm\ \ ,\ \ }\omega {\rm =}\frac{{\rm 2}\pi }{{\rm T}}=6.35\Rightarrow T=0.99\ {\rm s}\ \]
By setting $x=8.47\, {\rm cm}$ and solving for $t$, we obtain
\[8.47=12.4{\cos \left(6.35t\right)\ }\Rightarrow {\cos 6.35t\ }=0.68\ \]
\[6.35t={{\cos }^{-1} 0.68\ }\Rightarrow t=0.129\ {\rm s}\]
In above, we have taken the inverse of cosine from both sides.
A simple harmonic oscillator has an amplitude of ${\rm 3.50\ cm}$ and a maximum speed of ${\rm 20.0\ cm/s}$. What is its speed when the displacement is ${\rm 1.75\ cm}$?
In the simple harmonic oscillation, the position and velocity is given by
\[x=A{\cos (\omega t+\alpha\ })\ \ \]
\[v=\frac{dx}{dt}=-A\omega\,{\sin \left(\omega t+\alpha\right)\ }\]
The term $A\omega$ is said the maximum velocity of the oscillatory system.
From the problem the given information is
\[A=3.5\ {\rm cm\ ,\ }{{\rm v}}_{max}=20\frac{{\rm cm}}{{\rm s}}\ \]
By definition of the maximum speed, find the angular velocity of the system
\[v_{max}=A\omega\to 20=3.5\omega\Rightarrow \omega=5.71\ {{\rm s}}^{{\rm -}{\rm 1}}\]
Squaring and summing both sides of $x\ $and $v$ equations with each other, we can get an equation that relates $x$ and $v$ at each time
\[x^2=A^2\,{{\cos }^2 \left(\omega t+\alpha\right)\ }\ \ ,\ \ v^2=A^2\omega^2{{\sin }^2 \left(\omega t+\alpha\right)\ }\]
\[\Rightarrow \ x^2+\frac{v^2}{\omega^2}=A^2\ \]
Setting $x=1.75\ {\rm cm}$ and $A=3.5\ {\rm cm}$, we obtain the desired velocity
\[{\left(1.75\right)}^2+\frac{v^2}{{\left(5.71\right)}^2}={\left(3.5\right)}^2\Rightarrow v=17.3\ {\rm m/s}\]
A $5.88\ {\rm kg}$ mass is connected to a spring and set into oscillation with a period of $2.86\, {\rm s}$ on a frictionless horizontal surface. Whenever this mass passes through the system's equilibrium position, its velocity has an absolute value of $13.3\, {\rm m/s}$.
(a) What is the total energy of this system?
(b) What is the spring constant of the spring?
(c) What is the amplitude of this oscillation?
(a) In the spring-object system, when the spring passes through the equilibrium position, object has its maximum velocity. Therefore, $v_{max}=13.3\ {\rm m/s}$. write out the total mechanical energy of the system as
\[E_{tot}=\frac{1}{2}mv^2+\frac{1}{2}kx^2\]
\[x=0\to \ v_{max}=13.3\frac{{\rm m}}{{\rm s}}\Rightarrow E_{tot}=\frac{1}{2}mv^2_{max}+0=\frac{1}{2}\left(5.88\right){\left(13.3\right)}^2=520{\rm \ J}\]
This energy remains constant.
(b) Recall that for such a system we have,
\[T=2\pi\sqrt{\frac{m}{k}}\Rightarrow T^2=4p^2\frac{m}{k}\Rightarrow k=4\pi^2\frac{m}{T^2}=\frac{4\pi^2\left(5.88\right)}{{\left(2.86\right)}^2}=28.4\ {\rm N}\]
(C) In the simple harmonic motion (SHO), when the system reaches the maximum distance from the equilibrium position, we call this point as the amplitude of the motion i.e. $x=A$. In this moment velocity is zero $v_A=0$.
\[E(x=A)=\frac{1}{2}mv^2_A+\frac{1}{2}kA^2=0+\frac{1}{2}kA^2\]
\[\Rightarrow A=\sqrt{\frac{2E}{k}}=\sqrt{\frac{2\left(520\right)}{28.4}}=6.05\ {\rm m}\]
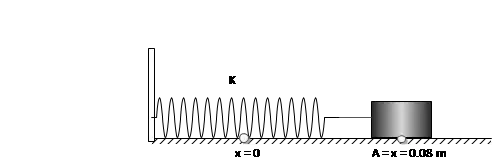
A $0.025\, {\rm kg}$ block on a horizontal frictionless surface is attached to an ideal massless spring whose spring constant is $150\ {\rm N/m}$. the block is pulled from its equilibrium position at $x=0\, {\rm m}$ to a displacement $x=+0.08\, {\rm m}$ and is released from rest. The block then executes simple harmonic motion (SHO) along the horizontal $x$ axis. When the displacement is $x=0.024\, {\rm m}$, what is the kinetic energy of the bock?
The conservation of mechanical energy in the SHO is written as $E=\frac{1}{2}kA^2=\frac{1}{2}mv^2+\frac{1}{2}kx^2+U(x)$ where the $\frac{1}{2}kA^2$ is a constant of motion ($A$ is the maximum displacement or amplitude of the oscillation) and $U(x)$ is the potential energy of the object. Therefore,
\[E=\frac{1}{2}kA^2=\underbrace{\frac{1}{2}mv^2}_{KE}+\frac{1}{2}kx^2\]
Since the object sits on the ground so $U\left(x\right)=0$.
\[\Rightarrow KE=\frac{1}{2}k\left(A^2-x^2\right)=\frac{1}{2}\left(150\right)\left({\left(0.08\right)}^2-{\left(0.024\right)}^2\right)=0.437\ {\rm J}\]
A uniform meter stick is freely pivoted about the $0.2\ {\rm m}$ mark. If it is allowed to swing in a vertical plane with a small amplitude and friction, what is the frequency of its oscillations?
This is a physical pendulum. In such a pendulum the period of the motion is given by
\[T=2\pi\sqrt{\frac{I_{pivot}}{mgL_{CM}}}\]
Where $I_{pivot}\ $is the moment of inertia of the pendulum about its pivot and  $L_{CM}$ is the distance of CM to its pivot. In this case, since the rod is uniform so its center of mass is located in the center of rod. The moment of inertia of a uniform rod with length $L$ about the axis through the CM is $\frac{1}{12}ML^2$. Now we must use the parallel axis theorem to find the $I$ about the pivot as
$L_{CM}$ is the distance of CM to its pivot. In this case, since the rod is uniform so its center of mass is located in the center of rod. The moment of inertia of a uniform rod with length $L$ about the axis through the CM is $\frac{1}{12}ML^2$. Now we must use the parallel axis theorem to find the $I$ about the pivot as
\[I_{pivot}=I_{CM}+Ml^2=M\left(\frac{1}{12}L^2+l^2\right)\]
\[\Rightarrow T=2\pi\sqrt{\frac{M\left(\frac{1}{12}L^2+l^2\right)}{Mgl}}=\sqrt{\frac{\frac{1}{12}{\left(1\right)}^2+{\left(0.3\right)}^2}{(9.8)(0.3)}}=1.525\ {\rm s}\]
A ${\rm 3.0\ kg}$ mass attached to a spring oscillates on a frictionless table with an amplitude $A\ =\ 8.0\times {10}^{-2}\ {\rm m}$. Its maximum acceleration is ${\rm 3.5\ m/}{{\rm s}}^{{\rm 2}}$ . What is the total energy of the system?
By the Hooke's law, the force $F_S$ exerted on the mass which is attached to a spring is $F_s=-kx$, where $x$ is the displacement from equilibrium (in this problem, the maximum displacement that is amplitude $A$ is given. So by the 2${}^{nd}$ law of motion we have
\[\Sigma F=ma\to kx=ma\Rightarrow \ k\underbrace{x_{max}}_{A}=ma_{max}\Rightarrow k=\frac{3\times 3.5}{8\times {10}^{-2}}=130\frac{{\rm N}}{{\rm m}}\]
Recall that in the spring- object systems the total energy is given by $E_{tot}=\frac{1}{2}kA^2$
\[E_{tot}=\frac{1}{2}\left(130\right){\left(8\times {10}^{-2}\right)}^2=0.416\ {\rm J}\]
One block of mass ${\rm 1\ kg}$ is connected on two sides by two springs of different stiffnesses. The block rests on a frictionless surface. The block is displaced by ${\rm 5\ cm}$ from its equilibrium position and released from rest.
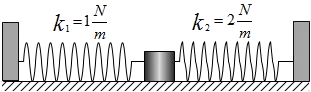
(a) What is the frequency of ensuing oscillation?
(b) What is the speed of the block when it passes the equilibrium position?
(c) When the block is passing through the equilibrium point where the springs are unstrained, another block of equal mass and speed as the first block is attached to it. What is the new amplitude of the oscillation?
(a) Suppose the mass is displaced $x$ from its equilibrium to the right. By Hooke's law the spring $1$ and $2$ act restoring forces $F_1$ and $F_2$ to the left on the mass. So the net restoring force on the mass equals $F_s=-F_1-F_2=-\left(k_1+k_2\right)x$.This is similar to the situation in which we have a spring with spring constant $k=k_1+k_2$. So
\[\omega=\sqrt{\frac{k_2+k_1}{m}}=\sqrt{\frac{1+2}{1}}=1.73\frac{{\rm rad}}{{\rm s}}\]
The frequency is related to the $\omega$ by the $f=\frac{\omega}{2\pi}=\frac{1.73}{2\pi}=0.28\ {\rm Hz}$
(b) Use the conservation of energy between releasing and equilibrium points.
\[E_i=E_f\to \frac{1}{2}kA^2=\frac{1}{2}mv^2\Rightarrow v=\sqrt{\frac{k}{m}}A=\sqrt{\frac{1+2}{1}}\left(0.05\right)=0.087\frac{{\rm m}}{{\rm s}}\]
Where $A$ is the maximum displacement of the mass from equilibrium(its amplitude)
(c) Use again the conservation of mechanical energy as follows
\[E_i=E_f\to \frac{1}{2}\left(m+m^{'}\right)v^2=\frac{1}{2}kA^{{'}^2}\]
\[\Rightarrow A^{'}=\sqrt{\frac{m+m}{k}}v=\sqrt{\frac{2\left(1\right)}{3}}\left(0.087\right)=7.1\ {\rm cm}\]
A steel wire $2.00\, {\rm m}$ long with a circular cross section must stretch no more than $0.2\ {\rm cm}$ when a $900\, {\rm N}$ weight is hung from one of its ends. Calculate the minimum diameter that this wire must have. ( Young's modulus of steel is $2\times {10}^{11}{\rm \ Pa\ }$)
When a rod, wire or bar with cross sectional area $A$ is stretched or squeezed by a force $F$, its initial lengths $l_0$ changes to $l$. In this case, we define a concept called Young's modulus, which is a measure of stiffness of the material that is made the rod as
\[Y=\frac{\frac{F}{A}}{\frac{\Delta {\rm L}}{{\rm L}}}\]
Given data are $\Delta l=0.2\ {\rm cm}$, $l_0=2\ {\rm m}$, $Y=2\times {10}^{11}\ {\rm Pa}$, $F=900\ {\rm N}$
Use the Young's modulus definition and find the cross sectional area $A$
\[A=\frac{FL}{Y\Delta L}=\frac{900}{2\times {10}^{11}}\frac{2}{0.2\times {10}^{-2}}=4.5\times {10}^{-6}\ {{\rm m}}^{{\rm 2}}\]
Now by using the $A$ find the radius of the circular cross section
\[A=\pi r^2\]
\[\Rightarrow r=\sqrt{\frac{A}{\pi}}=\sqrt{\frac{4.5\times {10}^{-6}}{\pi}}=2.4\times {10}^{-3}\ {\rm m=2.4\ mm}\]
A harmonic oscillator is made by using a $0.3\, {\rm kg}$ frictionless block and an ideal spring with an unknown force constant. The oscillator is found to have a period of $0.2\, {\rm s}$.
(a) Calculate the force constant of the spring.
(b) The block is now pulled back, so that its maximum displacement from equilibrium is $0.05\, {\rm m}$ and it is released from this point. Calculate the elastic energy in the spring at this maximum displacement.
(c) Using conservation of energy, calculate the maximum velocity of the block, as it passes through the equilibrium position (where the displacement is zero).
(a) Recall that the period of such a system is
\[T=2\pi\sqrt{\frac{m}{k}}\Rightarrow k=\frac{4\pi^2}{T^2}m=4\pi^2\frac{0.3}{{\left(0.2\right)}^2}=296\frac{{\rm N}}{{\rm m}}\]
(b) We know that the total mechanical energy of the system of spring + block is $E_{tot}=\frac{1}{2}kA^2$ where $A$ is the maximum displacement from equilibrium position ( which is called Amplitude). Therefore,
\[E_{tot}=\frac{1}{2}\left(296\right){\left(0.05\right)}^2=0.37\ {\rm J}\]
(c) By using the conservation of mechanical energy between the maximum stretching (i) and equilibrium (f) points, we obtain
\[E_i=E_f\Rightarrow \underbrace{\frac{1}{2}kx^2_i}_{elastic\ potential}+\underbrace{\frac{1}{2}mv^2_i}_{kinetic\ energy}=\frac{1}{2}kx^2_f+\frac{1}{2}mv^2_f\]
\[\Rightarrow \frac{1}{2}kA^2+0=0+\frac{1}{2}mv^2_f\Rightarrow v_f=A\sqrt{\frac{k}{m}}=\left(0.05\right)\sqrt{\frac{296}{0.3}}=1.57\frac{{\rm m}}{{\rm s}}\]
This is the maximum velocity at the equilibrium point since at this point all of the mechanical energy is converted to the kinetic energy
A cup of mass $m=0.2\, {\rm kg}$ rests on a frictionless horizontal surface and is mounted between two springs of equal constant $k_1=100\, {\rm N/m}$ as shown in the figure below. If the cup of mass $m$ is displaced a distance $A=0.1\, {\rm m}$ and released, it will undergo simple harmonic motion.
(a) What is the period of its oscillation?
Consider now what happens if a piece of putty of mass $m/2$ is dropped into the cup and sticks to it. If this occurs when the right spring is at its maximum compression.
(b) What is now the amplitude of oscillation?
(c) What is now the frequency of the oscillation?
If this occurs when the block is moving through its equilibrium position
(d) How much energy was lost in the collision?
(e) What is now the amplitude of the motion?
(a) Let us consider the mass $m$ is displaced to the right. We know that the spring force is a restoring force that is it tends to come back to the equilibrium position of the spring i.e. $F_s=-kx$ where $x$ is distance from the equilibrium point. When the mass moved to the right, both the right and left springs exert $F_s$ toward the left on the mass (to the equilibrium points of the springs). So the total force acting on the mass is $F_{tot}=2F_s=-2kx$. Using Newton's second law, we have
\[F=m\frac{d^2x}{dt^2}\Rightarrow \ -2kx=m\frac{d^2x}{dt^2}\]
\[\Rightarrow \frac{d^2x}{dt^2}+\frac{2k}{m}x=0\]
(recall that the acceleration is the second derivative of displacement with respect to time). The equation above is analogous to the equation of simple harmonic motion i.e. $\ddot{x}+\omega^2x=0$, (dot represents the time derivative). By comparing with this we can obtain the angular frequency $\omega=2\pi/T$.
\[\therefore \omega=\sqrt{\frac{2k}{m}}=\frac{2\pi}{T}\Rightarrow T=2\pi\sqrt{\frac{m}{2k}}\]
(b) Amplitude in simple harmonic motion is the maximum displacement from equilibrium point. Here, the right spring is in this situation. At this point the velocity of the mass is zero. Apply the conservation of mechanical energy between the old and new amplitude points. Recall that in the part (a) we calculate the effective constant spring of the system is $2k$. Therefore,
\[E_i=E_f\Rightarrow \frac{1}{2}\left(2k\right)A^2_i=\frac{1}{2}\left(2k\right)A^2_2\Rightarrow A_1=A_2\]
$\frac{1}{2}kA^2$ is the elastic potential energy of springs. Thus we see that the amplitude does not change!
(c) In part (a), the angular frequency of a simple harmonic motion is determined as
\[\omega=\sqrt{\frac{k^{'}}{m^{'}}}=2\pi f\]
Where $k^{'}$ is the effective constant spring. In this system, $k^{'}=2k$ and $m^{'}=\frac{m}{2}+m$
Therefore,
\[f=\frac{1}{2\pi}\sqrt{\frac{2k}{\frac{3}{2}m}}=\frac{1}{p}\sqrt{\frac{100}{3(0.2)}}=4.1\ {\rm Hz}\]
(d) Let us consider the masses and springs as an isolated system. Since there are no external forces (friction of the surface or air resistance), the momentum of the system is conserved. After the collision, the putty sticks to the mass $m$, so we have a perfectly inelastic collision. In such a collision, some of the initial kinetic energy dissipated (kinetic energy is not conserved due to the internal friction). Therefore, the conservation of momentum gives
\[P_i=P_f\Rightarrow mv_0=\left(m+\frac{m}{2}\right)v\Rightarrow v=\frac{2}{3}v_0\]
Where $v_0$ and $v$ are the velocities before and after the collision. From the conservation of total energy, we obtain
\[K_i=K_f+Q\Rightarrow \ \frac{1}{2}mv^2_0=\frac{1}{2}\left(m+\frac{m}{2}\right)v^2+Q\]
\[\Rightarrow Q=\frac{1}{2}mv^2_0-\frac{3}{4}m{\left(\frac{2}{3}v_0\right)}^2=\frac{1}{6}mv^2_0\]
$Q$ is the heat produced during this collision or the amount of energy lost. Now we must find the velocity of the mass $m$ when it is moving through its equilibrium position. In the simple harmonic motion, at the ends of the path the velocity is zero and at the equilibrium point it is the maximum value. Its magnitude is given by $v_{max}=A\omega$. Thus $v_{max}=v_0$. By substituting this into the above, we obtain
\[Q=\Delta K=\frac{1}{6}m{\left(A\omega\right)}^2=\frac{1}{6}mA^2\left(\frac{2k}{m}\right)=\frac{1}{3}kA^2\]
\[\Rightarrow Q=\frac{1}{3}\left(100\right){\left(0.1\right)}^2=0.33\ {\rm J}\]
Where we have used the $\omega=\sqrt{2k/m}$ in part (a).
(e) Apply the conservation of mechanical energy between the equilibrium position (i) and the maximum distance of the final position (f). at position (i) the springs neither stretched nor compressed i.e. $x=0$ so the elastic potential energy of them is zero. At position (f) the springs are in the maximum distance from the equilibrium i.e. $x=A_f$ and $v_f=0$, where $A_f$ is the final amplitude. Therefore,
\[E_i=E_f\to U_i+K_i=U_f+K_f\ \]
\[\Rightarrow 0+\frac{1}{2}\left(m+\frac{m}{2}\right)v^2=\frac{1}{2}\left(2k\right)A^2_f+0\]
\[\Rightarrow A_f=\sqrt{\frac{3m}{4k}}v\]
Recall from previous parts that
\[v=\frac{2}{3}v_0=\frac{2}{3}A_i\omega=\frac{2}{3}A_i\sqrt{\frac{2k}{m}}\]
By substituting $v$ into the $A_f$, we obtain
\[A_f=\sqrt{\frac{3m}{4k}}\left(\frac{2}{3}A_i\sqrt{\frac{2k}{m}}\right)=\sqrt{\frac{2}{3}}A_i\]
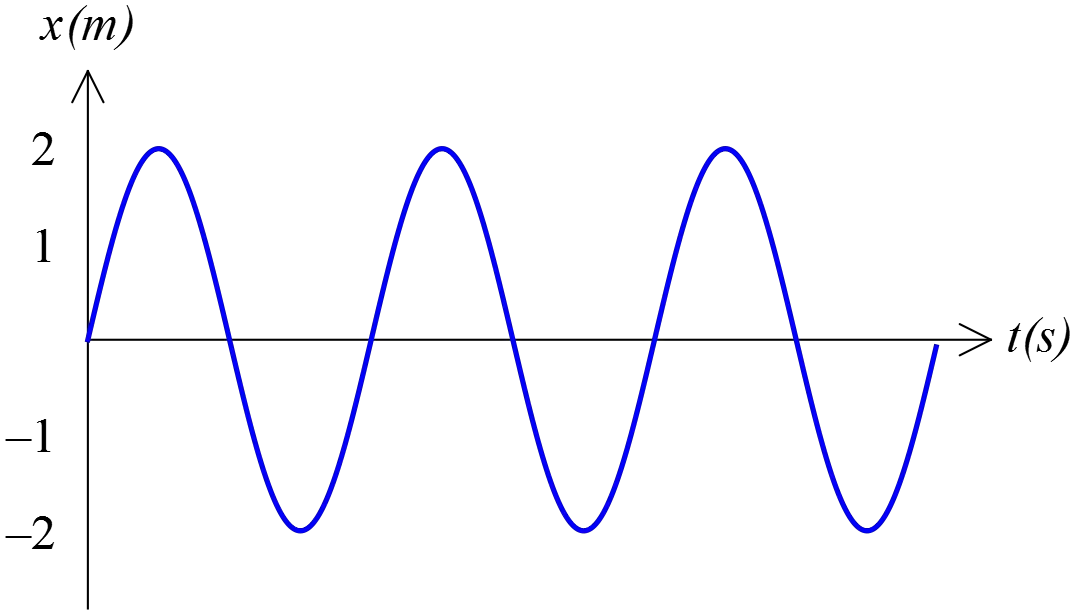
This plot shows a mass oscillating as $x=x_m\,\cos \left(\omega t-\phi \right)$. What are $x_m$ and $\phi$
(a) $1 {\mathrm m}\,.\,0^\circ$
(b) $2 {\mathrm m}\,.\,0^\circ$
(c) $2 {\mathrm m}\,.\,90^\circ$
(d) $4 {\mathrm m}\,.\,0^\circ$
All of the relevant quantities in a simple harmonic motion are related together by the following basic equation:
\[x(t)=A\,\sin (\omega t\pm \phi_0) \quad or \quad x(t)=A\,\cos (\omega t\pm \phi_0)\]
Where $(\omega t\pm \phi_0)$ is called the phase of oscillation. $\omega=\frac {2\pi}{T}=2\pi f$ is the angular frequency of oscillation. $\phi_0$ is the phase constant of the motion which is determined by the initial condition by setting $t=0$ in equation above
\[t=0 \to x\left(t=0\right)=A\,\cos (0\pm \phi_0) \to \phi_0=\cos^{-1} \left(\frac {x(0)}A\right)\]
Note: in graphs, the amplitude is the distance from the axis to the maximum point.
From the graph, the oscillating mass start from $x(t=0)=0$, therefore
\begin{gather*}
x_m=A=2 {\mathrm m} \\
and \quad \phi_0=\cos^{-1} \left(\frac{x(t=0)}A\right)=\cos^{-1} \left(\frac 02\right)=\cos^{-1}(0)\\
\therefore \ \ \phi_0=\cdots,-270^\circ,-90^\circ,90^\circ,270^\circ,\cdots
\end{gather*}
The correct answer is C.
A particles moves in simple harmonic motion according to $x=2\,{\,\cos (50t)\ }$, where $x$ is in meters and $t$ is in seconds. Its maximum velocity is:
(a) $100\,{\,\sin \left(50t\right)\ }\frac{\mathrm{m}}{\mathrm{s}}$
(b) $100\,{\,\cos \left(50t\right)\ }\frac{\mathrm{m}}{\mathrm{s}}$
(b) $100\frac{\mathrm{m}}{\mathrm{s}}$
(c) $200\frac{\mathrm{m}}{\mathrm{s}}$
(d) None of these
In the previous problem, stated that the equation of motion a SHM is as $x\left(t\right)=A{\,\cos (\omega t+{\phi }_0)\ }$. We know, from the kinematic, that the instantaneous velocity is derivative of displacement with respect to the time, $v=dx/dt$, therefore the velocity equation of a SHM is found as
\[v=\frac{dx}{dt}=-A\omega {\,\sin \left(\omega t+{\phi }_0\right)\ }=-v_{max}{\,\sin \left(\omega t+{\phi }_0\right)\ }\]
Where $v_{max}=A\omega \ $is the maximum velocity and is a positive number. Using the derivative of position function $x(t)$ we have
\[v=\frac{d}{dt}\left(2{\,\cos \left(50t\right)\ }\right)=-2\times 50{\,\sin \left(50t\right)\ }=-100{\,\sin (50t)\ }\]
Therefore the maximum velocity is $100\ \mathrm{m/s}$ and the correct answer is C.
If the length of a simple pendulum is doubled, its period will:
(a) Halve
(b) Increase by a factor of $\sqrt{2}$
(c) Decrease by a factor of $\sqrt{2}$
(d) Double
(e) Remain the same
The period of a simple pendulum of length $l$ is given by the well-known equation below
\[T=2\pi \sqrt{\frac{l}{g}}\]
Where $g$ is the gravitational acceleration of the place that the experiment is performed.
Therefore, if $l_2=2l_1$ we get
\[\frac{T_2}{T_1}=\sqrt{\frac{l_2}{l_1}}=\sqrt{\frac{2l_1}{l_1}}=\sqrt{2}\Rightarrow T_2=\sqrt{2}T_1\]
The correct answer is B.
MOST USEFUL FORMULA IN HARMONIC MOTIONS:
Period $T$ is time for one cycle.
Frequency is the number of cycles per unit time
\[f=\frac 1 T\]
Angular frequency $\omega=2\pi f=\frac {2\pi}{T}$
Restoring force in Simple Harmonic Motions(SHM):
\[F_x=-kx\]
Angular frequency in SHM:
\[\omega=\sqrt{\frac k m}\]
Displacement in SHM:
\[x(t)=A\,\cos \left(\omega t \pm \phi\right)\]
Velocity in SHM:
\[v=\frac{dx}{dt}=-A\omega\,\cos \left(\omega t \pm \phi\right)\]
Acceleration in SHM:
\[a=\frac {d^{2}x}{dt^{2}}=A\omega^2\,\cos \left(\omega t \pm \phi\right)\]
where $A$ is the maximum distance from equilibrium (amplitude)
Energy in SHM:
\[E=\frac 1 2 mv_x^2+\frac 1 2 kx^2=\frac 1 2 kA^2\]
Angular frequency in simple pendulum:
\[\omega=\sqrt{\frac g L}\]
Frequency of a simple pendulum:
\[f=\frac \omega {2\pi}=\frac 1{2\pi} \sqrt{\frac g L}\]
Angular frequency in physical pendulum:
\[\omega=\sqrt{\frac {mgd}{I}}\]
where $d$ and $I$ are the distance from axis of rotation to the center of gravity and moment of inertia about the axis,respectively.
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
