AP Physics 1 2025 FRQ 1: Detailed Step-by-Step Solution

In this post, the AP Physics 1 2025 Free Response Question 1 is broken down with clear explanations, step-by-step calculations, and key concepts to help you understand the solutions thoroughly. 

FRQ 1:

 

Solution to FRQ 1: 

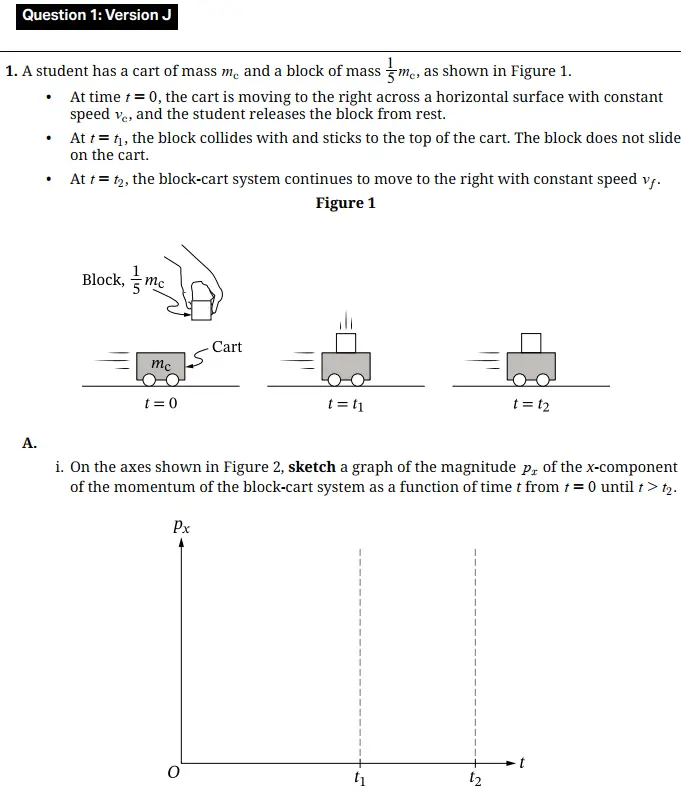
This question is about collisions, conservation laws, and defining a system in physics.

We’re looking at a cart and a block, and we’re defining our system to be both of them together. That’s super important: once you pick your system, you have to be clear about what counts as internal vs. external forces. We define them in physics as follows:

• Internal forces are the pushes and pulls happening inside the system (here, the block pushing on the cart and the cart pushing back on the block).
• External forces are forces coming from outside the system (like friction from the ground, or you pushing the cart).

Here’s the key idea: only external forces can change the momentum of a system. Since the block and cart only exert forces on each other during the collision, that’s all internal — meaning the total momentum of the block and cart system is conserved.

Part I: Momentum Conservation

The law of conservation of momentum says that the total momentum of a system stays constant if there are no external forces. That means \[p_{x-before}=p_{x-after}\] At $t=0$, the cart is moving, so it has momentum $m_c v_c$. The block is at rest, so its momentum is zero. Total momentum is \begin{align*} p_x &= m_{cart}v_{cart} + m_{block}v_{block} \\\\ &=m_c v_c \end{align*} When the block collides with the cart at $t=1$, they stick together, but this collision is internal to the system. So, the momentum of the block-cart system is still $m_c v_c$. After the collision, they move together at a slower speed (since the mass is bigger now), but with the same total momentum.

Therefore, the graph of $p_x$ vs. time is a straight horizontal line at $p_x=m_c v_c$, from $t=0$ through $t>2$. Momentum doesn’t budge unless there’s an external force. 
  

 

Part II: Finding the Final Speed

The initial total momentum is \[p_{initial} = m_c v_c +m_b v_b = m_c v_c \] because the block is at rest initially, ($v_b=0$). After the collision, the two objects become attached, so they will have a common speed, $v_f$. Then the total momentum after the collision is \begin{align*} p_{final} &= (m_b+m_c)v_f \\ &=\frac 65 m_c v_f \end{align*} According to the law of conservation of momentum, the total momentum is conserved or remains constant, $p_{initial}=p_{final}$. Solving for $v_f$, we obtain \begin{gather*} p_{initial} = p_{final} \\ m_c v_c = \frac 65 m_c v_f \\ \rightarrow \boxed{v_f = \frac 56 v_c} \end{gather*} So the cart and the block together moves at five-sixths the cart's original speed.

---

 

Part III: Kinetic Energy and Inelastic Collisions

Because the objects stick together, this is a completely inelastic collision. Momentum is conserved, but kinetic energy is not. Some of the initial kinetic energy turns into heat, sound, or deformation.

Therefore, the total kinetic energy after the collision is less than the total kinetic energy before the collision. We can write: \begin{gather*} K_{initial} = k_{final} + \text{heat}(Q) \\\\ \rightarrow \underbrace{\Delta K}_{Q} = K_{initial} - K_{final} \end{gather*} Note: explicitly state the initial and final kinetic energies has one point (1 pt). 

Now let's plug in the numbers. The block has mass $m_b=\frac 15 m_c$, and we found $v_f=\frac 56 v_c$ (1 pt). \begin{align*} \Delta K &= \frac 12 m_c v_c^2 -\frac 12 (m_c+m_b)v_f^2 \\\\ &=\frac 12 m_c v_c^2 \left(1- \frac 65 \frac{25}{36} \right) \\\\ &= \frac{1}{12} m_c v_c^2 \end{align*} Crunching through that algebra, you get: \[\Delta K= \frac{1}{12} m_c v_c^2 \] So, some kinetic energy has been “lost” (really transformed) during the collision. All these steps have one point (1 pt). 

---

 

Part B:

So, we’re looking at the cart and the new block as our system. The friction force between the block and the cart is an internal force since it’s happening inside the system. From Newton’s third law, we know internal forces come in equal-and-opposite pairs, so they cancel out when we’re looking at the system as a whole. 

That’s why internal friction between the block and cart cannot change the system’s total momentum.

As long as there’s no external force—like friction from the ground or something else— acting on the system in the x-direction during the time interval ($\Delta t$), the $x$-component of the momentum stays the same. That’s just conservation of momentum doing its thing: no external forces, no change in momentum. So, during ($\Delta t$), the $x$-component of the momentum of the block-cart system stays constant, just like before.

Extra note: if you bring in external friction from the ground, then momentum won’t be conserved anymore. The momentum would decrease over time, and your $p_x$ vs. time graph would slope downward after the collision instead of staying flat.
 

Published: Sep 9, 2025
Author: Dr. Ali Nemati