AP Physics 1 Formula Sheet: 2026 Edition
Check out this unique and comprehensive guide to AP Physics 1 formulas, freshly updated for 2026!
All equations are aligned with the College Board's AP Physics 1 curriculum.
Get the complete 31-page premium PDF with diagrams, examples, and high-resolution formula tables.
It’s a must-have resource for mastering AP Physics in 2026. Don’t miss out on this opportunity to boost your understanding and ace your exams!
Why is it important to review AP Physics 1 formulas?
Going over the formulas before the test is really important for a few reasons.
First, it helps you better understand the basic ideas that these formulas show.
Next, it makes you more skilled at using them, which lets you solve problems faster during the test.
Finally, it helps you remember them, making sure these formulas are ready in your mind when you need them.
Don’t forget that these formulas are the tools you’ll use to show what you know about physics on the test.
So, the more easily you are with them, the better you’ll do. Best of luck with your studies!
What topics will be covered on the 2026 AP Physics 1 Exam?
Kinematics: This topic deals with the motion of objects without considering the forces that cause them. You will learn about displacement, velocity, acceleration, graphs of motion, and projectile motion.
Dynamics: This topic deals with the forces that act on objects and how they affect their motion. You will learn about Newton’s laws of motion and various types of forces, including weight, friction, and normal forces. Additionally, you will explore their applications in scenarios such as inside an elevator and on a rough inclined plane.
Circular Motion and Gravitation: You’ll explore the physics of objects moving in a circle, the forces required to keep an object moving in a circle, and the law of universal gravitation.
Energy: This topic deals with the capacity to do work or transfer heat. You will learn about kinetic energy, potential energy, conservation of energy, and the work-energy theorem.
Momentum: This topic delves into the concept of momentum, which is the product of an object’s mass and velocity. It will guide you through the principles of momentum conservation, various types of collisions, and the intricacies of the impulse-momentum theorem.
Simple Harmonic Motion: This topic deals with the periodic motion of objects that oscillate back and forth around an equilibrium position. You will learn about amplitude, frequency, and period.
Torque and Rotational Motion: This topic deals with the tendency of a force to cause an object to rotate. You will learn about torque, rotational kinetic energy, and rotational dynamics.
Remember, understanding the concepts is crucial for doing well on the AP Physics exam. If you’re struggling with a topic, practice problems regularly.
AP Physics 1 Equations
Students, I recommend downloading the PDF of AP Physics 1 formulas crafted for the 2026 exam. It’s offline-accessible and has more formulas, detailed descriptions, and visual aids like figures and free-body diagrams. It’s a handy tool for your studies. Download today!
Unit 1: Kinematics
Displacement of an object is the change in the position of the object. It is a vector quantity.
Average velocity is displacement $\Delta x$ divided by the time interval $\Delta t$.
Average acceleration is the velocity change $\Delta v$ over a time interval $\Delta t$.
Kinematic equations for constant acceleration, $a=constant$
Practice Kinematics Problems Now
Kinematic equations for freely falling objects.
$g=9.8\,\rm m/s^2$, acceleration due to gravity.
Solve free-fall problems
Horizontal Motion ($a_x=0\, , \, v_x=\text{constant}$):
\begin{gather*} v_x=v_{x0}=v_0 \cos\theta \\ x=(v_0 \cos\theta)t \end{gather*}
Vertical Motion ($a_y=-g=\text{constant}$):
\begin{gather*} v_y=(v_0 \sin\theta)t -gt \\\\ y=v_0 \sin\theta -\frac 12 gt^2 \\\\ v_y^2=(v_0 \sin\theta)^2-2g\Delta y \end{gather*}
Range of projectile:
\[R=\frac{v_0^2 \sin 2\theta}{g}\]
Projectile Motion Equations
All equations assume $y$ is taken positive upward.
If $y$ is taken positive downward, the minus sign ($-$) in front of $g$ becomes a plus sign $+$.
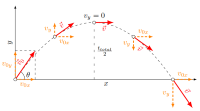
Try projectile motion practice problems.
Unit 2: Forces and Translational Dynamics
Newton's first law states that an object stays at rest or moves with constant speed in a straight line unless a net force acts on it.
- The net force acting on an object is defined as the vector sum of all external forces exerted on the object.
- $\vec{F}_{net}=\vec{F}_1+\vec{F}_2+\cdots$ is the vector sum of all forces acting on the object.
- No net force, no change in the object's velocity.
- The tendency of an object to retain its original state of motion is called inertia.
Newton's second law states that the acceleration of an object is directly proportional to the net force $F_{net}$ applied to it and inversely proportional to its mass $m$.
- No net force $\rightarrow a=0 \Rightarrow v=\text{const}$
- The SI unit of force is the newton \[1\,\rm{N} \equiv 1\,\rm{kg \cdot m/s^2}\]
AP Note: If you are given several vectors and asked to find the object's acceleration vector, add all forces as vectors, then find the $\vec{a}$ by dividing by $m$.
Warning: Do not find individual magnitudes of the forces and add them like scalars.
Need help? Try practice questions 5 and 6 from the AP Physics forces problems set.
Newton's third law states that whenever object $1$ exerts a force on object $2$, the second object always exerts a force on the first object that is equal in magnitude but opposite in direction (the minus sign $-$).
Before moving on, make sure to check this out: all the key concepts and notes on Newton’s Third Law with practice problems, you’ll need for the exam.
Weight of a body near the Earth or other planet (with different $g$).
The magnitude of the kinetic friction force $f_k$ acting on an object moving on a rough surface.
The magnitude of the maximum static friction force acting on an object when it is on the verge of slipping.
In general, the kinetic coefficient is less than the static coefficient.
The magnitude of the centripetal acceleration of an object moving with constant speed $v$ in a circular path of radius $r$ is always directed toward the center of the circular path.
Newton's second law for uniform ($v=constant$) circular motion.
For such motion, a force is needed to keep an object moving around a circle.
The direction of this force is always toward the center of the circle.
Examples of these forces are the force of gravity (as in the motion of a satellite or moon around the Earth), the tension in a cord, or a component of normal force (as in the motion of a car rounding a banked curve)
The magnitude of the attractive gravitational force that an object of $m_1$ applies to an object of mass $m_2$ positioned at a center-to-center distance $r$.
$G=6.67\times 10^{-11}\,{\rm N\cdot m^2/kg^2}$ is a universal constant.
This formula is used primarily to find the magnitude of the Sun's force on planets, between two planets, or between a planet and its moon. In the AP Physics 1 exam, the order of magnitude estimates for the force will be asked for.
The amount of gravitational field $g$ produced by a planet of mass $M$ at a distance $d$ from the planet's center.
Substituting $M_{planet}=M_{earth}$ and $d=r_{earth}$ gives the value of free-fall acceleration at the surface of the Earth, $g=9.8\,\rm m/s^2$.
Unit 3: Work, Energy, and Power
The work done by a constant force $\vec{F}$ on an object while its displacement is $\Delta \vec{x}$.
$F$ is the magnitude of the applied force in newtons, $d$ is the magnitude of the displacement in meters, and $\theta$ is the angle between the direction of $\vec{F}$ and the direction of $\Delta \vec{x}$.
The sign of $\cos\theta$ determines the sign of the work.
The SI unit of work is the joule: $\rm 1\,J=1\,N\cdot m$
Work is a scalar quantity in physics.
Positive work: the applied force and the object's displacement are in the same direction, $\theta=0\rightarrow \cos\theta=1$. The system gains energy.
Negative work: the applied force and the object's displacement are in the opposite direction, $\theta=180^\circ \rightarrow \cos\theta=-1$. The system loses energy. Friction always does negative work.
Zero work: the external force points perpendicular to the object's displacement, $\theta=90^\circ \rightarrow \cos\theta=0$. There is no change in the energy of the system, like the work done by a normal force.
The gravitational potential energy of an object of mass $m$ at height $h$ (in meters) near the Earth's surface.
The gravitational potential energy equation for two objects located far away in space with infinity is taken as zero potential.
A single object cannot have gravitational potential energy.
(Translational) Kinetic energy is the energy of an object of mass moving at a speed of $v$. It is a scalar quantity. SI unit: joules ($\rm J$).
Notice that kinetic energy is always a positive value.
Elastic potential energy is the energy of a stretched or compressed spring as much $x$ from its equilibrium position.
$k$ is the spring stiffness constant with an SI unit of $\rm N/m$.
Conservation of total mechanical energy.
The work-energy theorem states that the net work done on an object of mass $m$ equals the change in its kinetic energy or that the work done by a non-conservative force $W_{nc}$ changes the total mechanical energy of a system ($E_{total}=U+K$).
The friction force is an example of a non-conservative force, meaning the work done by it depends on the path taken.
Power is defined as the rate of energy transfer, or the rate of work done on a system during a time interval of $\Delta t$.
SI unit: the watt, ($W=\rm J/s$)
Unit 4: Linear Momentum
Linear momentum is a vector quantity in physics that is defined as the product of an object's mass $m$ and its velocity $\vec{v}$.
Impulse is the product of the average external constant force $\vec{F}$ exerted on an object during a time interval $\Delta t$ and that time interval.
SI unit: $\rm N\cdot s$
The impulse-momentum theorem states that the impulse of a constant force delivered to an object equals the change in momentum of the object.
The area under the force vs. time graph is the impulse.
When no net external forces act on an isolated system, the total momentum of that system before an interaction is the same as after the interaction. This principle is called the conservation of momentum.
In all collisions, momentum is a conserved quantity.
In all elastic collisions, the momentum and kinetic energy of the system are conserved (or constant).
In an inelastic collision, the momentum is conserved, but kinetic energy is not.
$\Delta U_{int}$ is the energy of motion and interaction of microscopic particles making up the object, known as internal energy or heat energy.
In a totally inelastic collision, the colliding objects stick together and have a common speed after the collision.
Pro Tip: Want to see how these formulas work in action? Check out our detailed solution for the 2025 FRQ 1 here.
Unit 5: Torque and Rotational Dynamics
The radian is the unit for rotational motion. In the AP Physics 1 exam, for simplicity, take $2\pi=6.3$.
Rotational (angular) displacement (in radians) is analogous to the displacement in translational kinematics. $s$ is the length of the arc pivoted to the angle $\theta$.
The average rotational (angular) velocity of a revolving body. It is measured in $\rm rad/s$ or revolutions per minute ($\rm rpm$).
Angular velocity is a vector quantity in physics, meaning it has both a magnitude and a direction.
Rotational (angular) speed is the magnitude of rotational velocity.
The sign of $\omega$ is conventionally taken to be positive for counterclockwise turning and negative for clockwise turning.
One revolution ($\rm rev$) corresponds to a complete rotation around a circle. \[\rm 1\,rev=360^\circ \]
The average rotational (angular) acceleration. It is measured in $\rm rad/s^2$.
The linear speed of a rotating body is related to its rotational speed $\omega$.
The linear acceleration $a$ of a rotating object is related to its corresponding rotational acceleration $\alpha$.
Kinematic equations for rotational motion with constant angular acceleration.
For simplicity in the AP Physics 1 questions, choose $\theta_0=0$.
$\omega _0$ is the initial angular velocity at the initial time $t_0=0$.
$\omega$ and $\theta$ are the angular position and velocity, respectively, at time $t$.
$\bar{\omega}$ is the average angular velocity.
The torque provided by a force $\vec{F}$ exerted on an object at a distance $r$ from its rotation axis.
$r_{\bot}=r\sin\theta$ is called the lever arm and is defined as the perpendicular distance from the axis of rotation to the line along which the force acts.
$F_{\bot}$ is the component of the force perpendicular to $r$, the distance between the point of application of the force and the pivot point.
$\theta$ is the angle between $\vec{F}$ and $r$.
SI unit: Newton-meter ($\rm N\cdot m$)
Unit 6: Energy and Momentum of Rotating Systems
The product of rotational inertia $I$ on an object and its angular velocity $\omega$ is defined as angular momentum.
Angular momentum is a vector quantity in physics.
In the topic of rotational motion, the direction of vector quantities is usually shown with positive and negative signs.
$L$ is positive for counterclockwise rotation and negative for clockwise rotation.
It is analogous to linear momentum, $\vec{p}=m\vec{v}$.
It is necessary to define a rotational axis to find the angular momentum.
When the net torque acting on a rotating object is zero, its total angular momentum remains constant. This is known as the conservation of angular momentum.
For an extended object, $L=I\omega$.
For a point particle of mass $m$ moving at a speed of $v$, we have $L=mvr$, where $r$ is the closest distance of approach.
The angular acceleration $\alpha$ of an object equals the net torque produced by forces exerted on the object divided by its rotational inertia, $I$.
This is also known as Newton's second law for rotation.
The impulse-angular momentum theorem states that a change in angular momentum equals the net torque multiplied by the time the torque is exerted.
The rotational kinetic energy $K_r$ of an object is energy due to its rotation about a particular axis. This is rotationally analogous to translational kinetic energy, $K=\frac 12 mv^2$.
Unit 7: Oscillations
The magnitude of the force $F_s$ exerted by a spring on an object attached to it when it is compressed or stretched as much $x$ is given by Hooke's law. $k$ is the spring stiffness constant.
The period, $T$, is the time required to complete one back-and-forth cycle.
The frequency, $f$, is the number of cycles per second. These are defined for a general periodic motion.
SI unit of frequency is the hertz ($\rm Hz$), where $\rm 1\,Hz= 1\,s^{-1}$.
The period of oscillation for an object of mass $m$ on the end of a spring.
The frequency $f$ of vibration of an object attached to a spring.
The period of a simple pendulum of length $\ell$.
Note that the period of a simple pendulum depends only on its length and on the magnitude of the gravitational constant near the surface of that planet, like the Earth $g=9.8\,\rm m/s^2$.
This period does not depend on the mass of the object hanging at the end of the pendulum.
During a simple harmonic motion, the total energy converts continually from elastic potential energy when the object is at extreme positions to maximum kinetic energy position when passing through the equilibrium position, to a combination of energy types between these points.
The maximum elastic potential energy is at the extreme positions where the object is momentarily at rest.
The maximum kinetic energy is at the equilibrium position where $x=0$.
Unit 8: Fluids
The pressure $p$ is the magnitude of the perpendicular force $F_{\bot}$ exerted on a surface divided by the area of that surface.
- Pressure is a scalar quantity.
- The SI unit of pressure is \[\rm \frac{N}{m^2} \, \text{or} \, \rm{Pa}\]
- $1\,\rm N/m^2$ is equivalent to $1$ pascal ($\rm Pa$)
- Two units used in meteorology \begin{gather*} 1\,bar=10^5\,\rm Pa \\\\ 1\,millibar=100\,\rm Pa \end{gather*}
- Atmospheric pressure $p_{atm}$ is the pressure of the Earth's atmosphere. \begin{align*} \rm{1\,atm}&=1.013\times 10^5\,\rm{Pa} \\ &=14.7\,\rm{psi} =1.013\,\rm{bars} \\ &=1013\,\rm{millibars} \end{align*}
If the pressure at a point in a fluid is $p_1$, then at a depth $h$ below that point, the pressure $p_2$ is given by this formula.
- $\rho$ is the density of the fluid, and $g$ is the acceleration of gravity.
- The pressure increases linearly with depth. Due to the weight of the fluid above, the deeper you go, the greater the pressure.
- The pressure at a depth $h$ below an open surface of a fluid in a container is given by \[p=p_{atm}+\rho gh \]
- $p_{atm}$ is the pressure at the top of the fluid, which is the atmospheric pressure.
- For water, pressure increases by $1\,\rm{atm}$ for about every 10 meters of depth.
Pressure applied to an enclosed fluid is distributed undiminished to every part of the fluid and the walls of its container.
- The pressure depends only on the depth; the shape of the vessel does not matter.
- The pressure in a fluid is the same at all points that have the same elevation, despite the vessel's shape.
-
A hydraulic jack uses Pascal's law to magnify force. Two pistons with cross-sectional areas $A_1$ (small) and $A_2$ (large) are connected through a fluid-filled pipe. Force $F_1$ on the smaller piston creates pressure, transmitted equally to the larger piston, producing a magnified force $F_2$ with the following magnitude that enables heavy lifting. \[F_2=\frac{A_2}{A_1}F_1\]
The buoyant force $F_b$ is the net upward force exerted by a fluid of density $\rho_F$ on an object submerged in it.
- This force is responsible for objects floating or sinking in a fluid.
- $V_{dis}$ is the amount of fluid volume displaced by the object.
When a body is completely or partially immersed in a fluid, the fluid exerts an upward force on the body equal to the weight of the fluid that is displaced by the object.
- When an object is placed in a full glass of water, the amount of water that overflows is called displaced water.
The apparent weight of an object on which a buoyant force acts is related to the object's true weight by this formula.
The equation of continuity tells us that for an incompressible fluid, the product of velocity of flow and the cross-sectional area of the pipe is constant \[Av=\text{constant} \Rightarrow A_1v_1=A_2 v_2\]
- The product of $Av$ is called the volume flow rate \[\frac{V}{t}=Av\]
- Each side of the equation has units of $\rm m^3/s$.
Bernoulli's equation relates the pressure $p$, flow speed $v$, and elevation $y$ for any two points along a tube of flow \[p_1+\rho gy1+\frac 12 \rho v_1^2 = p_2+\rho g y_2 +\frac 12 \rho v_2^2\]
- Each term in the equation above has units of pressure, $\rm N/m^2$.
Torricelli's theorem is a direct application of Bernoulli's equation to an open vessel containing a fluid that escapes through a narrow opening of cross-sectional area $A$, located at a depth $h$ below the top surface of the liquid. \[v=\sqrt{2gh}\]
- $v$ is the liquid’s exit speed in $\rm m/s$.
Summary:
This article provides all the necessary formulas for AP Physics 1 and brief explanations tailored for students preparing for the 2026 AP Physics 1 exam.
Published: Dec 20, 2023
Last Updated: Jul 27, 2025
Author: Dr. Ali Nemati
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
