Archimedes' Principle: Equation with Solved Examples
Have you ever wondered why large and massive steel ships do not sink but a small coin does?
The answer lies in Archimedes' principle, which is closely related to the buoyant forces.
When objects are in fluids (such as water or even air!), two main forces act on them: the upward buoyant force and the downward gravitational force. The competition between these two forces determines whether an object sinks or floats in a fluid.
Here, we are going to learn about this topic with some basic and important solved examples.
This fundamental principle, discovered by a Greek mathematician in the sixth century B.C., states:
Any object wholly or partially submerged in a fluid is buoyed up by a force equal to the weight of the fluid displaced by the object.
When you lift a heavy object in a swimming pool, you are experiencing Archimedes' principle as water provides partial support, helping you overcome the weight of the object.
Using Archimedes' principle, we can also explain why hot air balloons ascend in the air.
When a body is placed into a fluid, an upward force is always exerted on it by the surrounding fluid, which partially or wholly offsets the downward gravitational force (weight). This upward force is called the buoyant force.
Derivation of Archimedes' principle:
Method 1: Simple argument
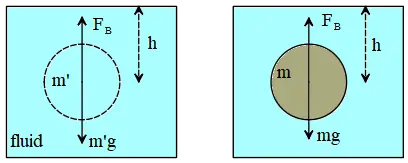
Suppose you have two bodies of the same size and shape placed at a certain depth in a fluid.
One is filled with an unknown substance of mass $m$, and the other is filled with the surrounding, which has a mass of $m'$.
Because both objects are at the same depth, the buoyant forces acting on them are the same.
These buoyant forces must be balanced with the objects' weight to maintain their equilibrium at the same depth.
For the object of mass $m$, according to Newton's second law of motion, $F_B=mg$. Similarly, for the object of mass $m'$, we have $F_B=m'g$. Therefore, \[mg=F_B=m'f\] As you can see, it is simpler to balance the buoyant force with a known weight $m'g$,( the weight of the fluid whose volume equals the volume of the original object) rather than with an unknown weight $mg$.
This is Archimedes' principle.
Method 2: The physical cause of the upward force exerted by fluids on objects is the pressure difference between the upper and lower sides of an object due to the different depths of the fluid.
At a depth $h$ below the fluid surface, the pressure is $P=P_0+\rho gh$, where $P_0$ is the pressure at the fluid surface and $\rho$ is the fluid density.
The lower side of an object sits at a greater depth, so by definition of pressure, $P=\frac FA$, there is a large force upon it.
Note that horizontal forces exerted on an object in a fluid are equal at the same depth, so their net effect is zero.
In fact, all horizontal forces exerted on an object of any shape cancel each other out.
What remains are the vertical forces applied on the top and bottom sides of the submerged body, whose vector summation gives the upward buoyant force $F_b$.
Applying Newton's second law and balancing all forces in the vertical direction, we obtain the following formula for Archimedes' principle
buoyant force = body's weight
or \[F_b=W\] Where buoyant force formula is written as the product of fluid's density, the displaced volume of the fluid by the object, and the gravitational constant $g=10\,{\rm m/s^2}$ or \[F_b=\rho_{fluid}\times V_{dis}\times g\]
Now is the time to solve some examples to understand Archimedes' principle.
Example: a block of wood floats in freshwater with two-fifths of its volume V submerged and in oil with 0.75V submerged. Find the density of (a) the wood and (b) the oil.
Solution: Since wood floats in water, its weight must be balanced with the buoyancy force.
(a) For a partially submerged body, the buoyant force $F_b$ is defined as the density of fluid $\rho_f$ times the displaced volume of fluid $V_{dis}$ times the gravitational acceleration $g$.
The wood displaces a volume of water equal to (2/5)V. This displaced water's weight equals the wood's weight (Archimedes' principle).
Therefore, we get: \begin{align*} W&=F_b \\ \\ \rho_{wood} \times V_{wood}\times g &=\rho_{water}\times V_{dis}\times g\\ \\ \rho_{wood}\times V_{wood} \times g&=(1)\left(\frac{2}{5}V_{wood}\right)g \\ \\ \rho_{wood}&=\frac25 \quad{\rm \frac{g}{cm^3}}\end{align*}
(b) Similarly, we can find the oil's density using the same approach: \begin{align*} \left(\rho Vg\right)_{wood}&=\left(\rho' Vg\right)_{oil} \\\\ (400)(V)g&=\rho_{oil}\, (0.75V)g\\\\ \Rightarrow \rho_{oil} &=\frac{400}{0.75} \\\\&=\frac{1600}{3}\quad {\rm kg/m^3}\end{align*}
Example: an iron object of density $7.8\,{\rm g/cm^3}$ appears 200 N lighter in water than in air.
(a) What is the volume of the object?
(b) How much does it weigh in the air?
Solution: Since the body becomes lighter in water, there must be an upward force acting on the object that cancels out some of the downward weight force. In fluids, this force is called floating or buoyancy force.
(a) According to Archimedes' law, $200\,{\rm N}$ is the buoyancy force acting on the body, which can be calculated as follows: \begin{align*} F_b &= \rho_{water} \times V_{object} \times g \\ \\ 200&=100\times V_{object}\times 10 \\ \\ \Rightarrow V_{object}&=\frac{2}{100}\quad {\rm m^3}\end{align*}
(b) The body's weight in air, $W=\rho V g$, is calculated as: \[W=(7800)\left(\frac{2}{100}\right)(10)=1560\,{\rm N}\] Where $V$ is the actual volume of the body.
As you can see above, one of the main applications of Archimedes' principle is finding the density of an unknown object.
Example: a wooden rectangular slab with surface area $5.7\,{\rm m^2}$, volume $V=0.6\,{\rm m^3}$ and density $600\,{\rm kg/m^3}$ is placed slowly in freshwater. By what depth $h$ is the slab submerged?
Solution: According to Archimedes' principle, water will apply an upward buoyant force on the slab, equal to the weight of the water displaced by the slab.
Thus, the buoyant force exerted on the slab is $F_b=m_{water}g=\rho_{water}V_{dis}g$, where $V_{dis}$ is the displaced volume of water or the volume of the slab underwater.
Let $h$ be the height of the slab from the bottom side. Thus, $V_{dis}=Ah$ where $A$ is the base area of the slab.
The weight of the slab is also given by $W=\rho_{slab}V_{slab}g$.
Next, using Archimedes' principle equation $F_b=W$, we get: \begin{align*}\rho_{water}\times (Ah) \times g&=\rho_{slab}\times V_{slab}\times g\\ \\ \Rightarrow h&=\frac{\rho_{slab}V_{slab}}{\rho_{water}A}\\ \\ &=\frac{600\times 0.6}{1000\times 5.7} \\ \\&=0.0632\quad {\rm m}\end{align*}
Criteria for floating or sinking:
Archimedes' principle gives us a rule of thumb to determine whether an object placed in a fluid will sink or float. According to this principle, if we write all forces applied by a motionless fluid on a submerged body as the upward buoyant force $F_b$ and downward weight force $W$, there are three situations depending on the sign of the net force $F_{net}=F_b \uparrow-W\downarrow$:
(1) Sinking: when $F_{net}<0$, the upward buoyant force is less than the downward weight force, causing the object to sink. \[\underbrace{\rho_{fluid}V_{fluid}g}_{buoyancy}<\underbrace{\rho_{obj}V_{obj}g}_{weight}\] For example, a stone is denser than water, so it sinks when placed in water.
(2) Floating: when $F_{net}>0$, the positive upward buoyant force balances the negative downward force of gravity (weight), causing the object to float on the surface of the fluid. \[\underbrace{\rho_{fluid}V_{fluid}g}_{buoyancy}=\underbrace{\rho_{obj}V_{obj}g}_{weight}\] Wood is less dense than water, so it floats.
(3) Neutral buoyancy: when $F_{net}=0$, the object remains motionless at that point where it is released in the fluid. This happens when the densities of the object and the fluid are equal. An example of neutral buoyancy is swimming fish. Fish have a swim bladder that can be filled with air along with their flesh to create a composite object with an average density that matches the density of the water, allowing them to neither sink nor float.
Question: How much of the iceberg's volume is under the sea level?
Solution: according to Archimedes' principle, since the iceberg floats on the water, the upward buoyant force equals its weight. The magnitude of the buoyant force is the product of the submerged volume of the iceberg, the water's density, and gravitational acceleration.
On the other hand, the weight of the iceberg is the product of its actual volume, the density of the iceberg, and gravitational acceleration.
Applying the floating conditions to find the fraction of the iceberg's volume below sea level, we get: \begin{align*}F_b&=W\\ \rho_{SW}V_{in-water}g&=\rho_{IB}Vg\\ \\ \Rightarrow \frac{V_{in-water}}{V}&=\frac{\rho_{IB}}{\rho_{SW}}\\ \\ &=\frac{0.92\times 10^{3}}{1.025\times 10^3} \\ \\ &=0.9\end{align*} Where in above $\rho_{IB}$ and $\rho_{SW}$ are the densities of iceberg and seawater, respectively. As you can see, about 90% of the volume of an iceberg is underwater.
Author: Ali Nemati
Page Created: 1/31/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
