Buoyant Force Formula with Solved Examples
In this tutorial, we will explore the buoyant force formula through a problem-solving approach.
You may have seen a ship or a boat floating on water. But what makes some objects float or sink in fluids?
Let’s try an experiment.
Attach a dense object to a spring scale and measure its weight. Then, immerse it in water and measure its weight again. You will notice that the scale reading in water is lower than that in air.
Why is that?
We can infer that there is an upward force acting on the object in the fluid (for example, water) that counteracts the downward gravitational force (weight) resulting in a lower weight, called apparent weight, in the fluid.
This is a common phenomenon that happens in all fluids when an object with a different density is submerged in it.
The force exerted by a fluid on an object that is completely or partially submerged in it is called buoyant force and its magnitude is equal to the weight of the fluid displaced by the object.
This upward force, which is called the buoyant force, is not a new type of force.
It arises from the pressure difference between the upper and lower surfaces of a submerged object in a fluid.
Origin of the buoyant force formula:
Consider a body submerged (say, a cube) in a fluid. The fluid exerts forces on all sides of the cube.
The forces in the horizontal direction are equal and opposite, so they cancel out. (This is because they are at the same depth from the fluid surface, so the pressure is the same.)
The forces in the vertical direction are different because the top and bottom sides are at different depths of the fluid.
We know that the pressure increases with depth, so the force on the bottom side is larger than the force on the top side. This results in a net upward force, which is called the buoyant force.
But how is the buoyancy force formula derived?
To find the buoyant force, let’s simplify the problem by considering a cube of height $h$ and base area $A$ that is completely submerged in a fluid with density $\rho_f$.
As shown in the figure, the fluid exerts vertical forces on the cube due to the water pressure at different depths. The force $F_1$ acts downward on the top surface of the cube, while the force $F_2$ acts upward on the bottom surface of the cube.
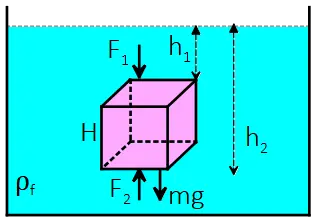
These are the only vertical forces that the fluid applies to the cube.
The horizontal forces cancel out since they are equal and opposite.
By adding the vertical forces, we get a net upward force, which is the buoyant force. We can derive the formula for the buoyant force as follows: \begin{align*} F_{net} &= F_2-F_1\\ \\&=P_2A-P_1A\\ \\&=(\rho_f gh_2)A-(\rho_g g h_1)A\\ \\&=\rho_f g(h_2-h_1)A\\ \\&=\rho_f V_{dis}g \end{align*} In the above derivation, we used the following facts: the pressure at a depth $h$ below the fluid surface is $P=P_0+\rho_f gh$ where $P_0$ is the surface pressure.
Therefore, the buoyant force formula is the product of the fluid density $\rho_f$, the displaced fluid volume $V_{dis}$, and the gravitational constant $g$. \[F_b=\rho_f V_{dis} g\]
We can also use the definition of density as the ratio of mass to volume, $\rho=\frac mV$, to find another useful equation for buoyant force as \[F_b=m_f g\] where, in this version, $m_f$ is the mass of the fluid displaced by the object submerged in it.
Example (1): A solid cylinder with base area $A=20\,{\rm cm^2}$ is placed completely underwater as shown in the figure. Calculate the difference between the forces exerted by the water on the upper and lower bases of the cylinder. ($g=10\,{\rm m/s^2}$ and $\rho_{water}=1\,{\rm g/cm^3}$).
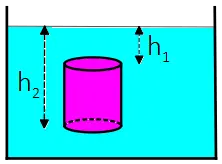
Solution: The water exerts two forces $F_1=P_1 A$ and $F_2=P_2 A$ on the upper and lower bases of the cylinder, respectively. The pressure at depth $h$ of a fluid with density $\rho$ is given by $P=\rho gh$.
The upper base is at depth $h_1=0.1\,{\rm m}$, so the pressure at that depth is $P_1=1000\times 10\times 0.1=1000\,{\rm Pa}$.
The lower base is at depth $h_2=0.5\,{\rm m}$, so the pressure at that depth is $P_2=1000\times 10\times 0.5=5000\,{\rm Pa}$.
The difference in forces is the upward buoyant force exerted on the cylinder by the water. $\Delta F=F_2-F_1=(P_2-P_1)A$, so we have \begin{align*}\Delta F&=F_2-F_1=(P_2-P_1)A\\&=(5000-1000)20\times(0.01)^2 \\&=8\quad {\rm N}\end{align*}
We can also find it using the buoyant force equation as $F_b=\rho_{water}V_{body}g$, where $V_{body}$ is the volume of the cylinder submerged in the water (here, the whole cylinder is submerged). \begin{align*}F_b&=\rho_{water}V_{body}g\\ &=(1000)(40\times 20)\times 10^{-5}\times 10\\&=8\quad {\rm N}\end{align*} The volume of the cylinder is the product of the base area ($A=20\,{\rm cm^2}$) and the height ($h=40\,{\rm cm}$).
The buoyant force formula was derived for a simple shape, a cube, but it can be shown that it is valid for any shape.
Key points about the buoyant force formula:
- The mass in the formula is the mass of the fluid that is displaced by the object, not the mass of the object itself.
- The formula works for any shape, because any shape can be broken down into many tiny cubes, and the formula applies to each cube.
- The buoyant force only depends on the density of the fluid $\rho_f$, not the density of the object. It does not matter what material the object is made of, whether it is wood or iron. The buoyant force is the same as long as the object displaces the same amount of fluid.
The example below shows what is meant by displaced volume in the buoyancy force equation.
Example (2): A rectangular container of ethanol with density $\rho_{eth}=800\,{\rm kg/m^3}$ floats in the liquid of density $\rho_{f}=1200\,{\rm kg/m^3}$. Height and base of the container are $H=6\,{\rm cm}$ and $A=20\,{\rm cm^2}$, respectively. $h=4\,{\rm cm}$ of its height is in the fluid. Find the buoyancy force exerted on the container.
Solution: The buoyant force is the weight of the fluid that is displaced by an object submerged in it. We can write it as $F_b=m_f g$ or $F_b=\rho_f V_{dis}g$, where $m_f$ is the mass of the displaced fluid, and $V_{dis}$ is the volume of the object under the fluid surface.
In this problem, the volume of the object under the fluid surface is $V_{dis}=A\times h$, where $A$ is the base area and $h$ is the height of the object. Substituting this into the buoyant force formula, we get \begin{align*}F_b&=\rho_{f}V_{dis}g\\&=\rho_f \times (Ah)g\\&=(1200)(20\times 4)\times 10^{-5}\times 10\\&=9.6\quad {\rm N}\end{align*}
This is the buoyant force that acts upward on the object.
The buoyant force is based on Archimedes' principle, which states that:
Any object that is wholly or partially submerged in a fluid experiences a buoyant force equal to the weight of the fluid displaced by the object.
Example(3): A piece of wood with density $\rho_{wood}=0.6\,{\rm g/cm^3}$ floats on the surface of the water. What is the ratio of the portion of the wood submerged in the water to that of outside the water? ($\rho_{water}=1\,{\rm g/cm^3}$)
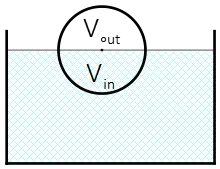
Solution: The wood floats on water because its density is lower than that of water. The weight of the wood is balanced by the upward buoyant force exerted by the water. Using the buoyant force formula and the weight formula, we get: \begin{align*} \text{buoyant force}&=\text{weight}\\ \\ \rho_{fluid}V_{dis}g&=\rho_{body}V_{body}g\\ \\ \Rightarrow \frac{V_{dis}}{V_{body}}&=\frac{\rho_{body}}{\rho_{fluid}}\\ \\ &=\frac{0.6}{1}\\ \\ \Rightarrow V_{fluid}&=0.6\, V_{body}\end{align*} Here, $V_{dis}$ is the volume of the water displaced by the wood, and $V_{body}$ is the total volume of the wood.
To find the volume of the wood that is above the water, we can use the following equation: \begin{align*} V_{wood}&=V_{wood-in}+V_{wood-out}\\ \\V&=0.6V+V_{wood-out} \\ \\\Rightarrow& V_{wood-out}=0.4V\end{align*} Here, $V_{out}$ is the volume of the wood that is outside the water.
Therefore, the volume of the wood that is inside the water is $V_{wood-in}=0.6V$ and the volume of the wood that is outside the water is $V_{wood-out}=0.4V$. Their ratio is $\frac 32$.
The buoyancy formula can be used to find the density of a fluid if we know the density of an object that floats in it. For example, consider the following problem:
Example (4): A piece of wood floats in water so that two-thirds of its volume $V$ is beneath the water level. When the same piece of wood is placed in oil, the submerged volume is $0.8V$. Find the density of (a) the wood and (b) the oil.
Solution: The object floats on the fluids (water and oil) so the downward gravitation force and upward buoyant force must balance each other.
Recall that the buoyancy force formula is the fluid density times the volume of the part of the object beneath the fluid level times the gravitational constant, i.e., $F_b=\rho_f V_{dis}g$.
In the case of water, the volume of the fluid displaced by the wood is, i.e., $V_{dis}=2/3 V$, since two-thirds of the wood's volume is submerged. Therefore, equating the weight and the buoyant force, we get: \begin{align*} F_b&=mg\\ \rho_{water}V_{dis}g&=\rho_{wood}Vg\\ (1000)(2/3 V)&=\rho_{wood}\times V\\ \Rightarrow \rho_{wood}&=\frac{2000}{3}\quad{\rm \frac{kg}{m^3}}\end{align*}
In the case of oil, the volume of the fluid displaced by the wood is $V_{dis}=0.8 V$, since $80\%$ of the wood's volume is submerged. Using the same logic, we get: \begin{align*} F_b&=mg\\ \rho_{oil}V_{dis}g&=\rho_{wood}Vg\\ \\\rho_{oil}(0.8 V)&=\underbrace{\rho_{wood}}_{2000/3}\times V\\ \\ \Rightarrow \rho_{oil}&=834 \quad{\rm \frac{kg}{m^3}}\end{align*} Therefore, the density of the wood is $\frac{2000}{3}\,\rm kg/m^3$ and the density of the oil is $834\,\rm kg/m^3$.
Another application of the buoyant force equation is to find the apparent weight of objects in fluids. Consider the following example:
Example (5): An iron object has a density of $7.8\,{\rm g/cm^3}$ and appears 200 N lighter in water than in air.
(a) What is the volume of the object?
(b) How much does it weigh in the air?
Solution: Since the body has become lighter in water, there must be an upward force acting on the object, which cancels some downward weight force. In fluids, this force is called floating or buoyancy force.
Note: 200 N is the buoyant force that acts on the iron object when it is submerged in water. It is the force that makes the object appear lighter in water than in air. You can find this force by using Archimedes’ principle.
(a) According to Archimedes’ principle, the buoyant force is equal to the weight of the fluid displaced by the object. Therefore, we can use the following equation to find the volume of the object: \begin{align*} F_b &= \rho_{water} \times V_{object} \times g \\ \\ 200&=1000\times V_{object}\times 10 \\ \\ \Rightarrow V_{object}&=\frac{2}{100}\quad {\rm m^3}\end{align*} Note that $V_{object}$ is volume of the water displaced by the iron or explicitly, part of the iron underwater (All of it).
(b) The weight of the object in air is given by the product of its mass and gravity. We can find its mass by multiplying its density and volume: \[W=\rho Vg=(7800)\left(\frac{2}{100}\right)(10)=1560\,{\rm N}\] where, here, $V$ is the actual volume of the object.
Example (6): An object with a mass of 150 kg is thrown into the water and displaces a volume of 100 liters of water. Will the object sink or float?
Solution: To see what happens after throwing, we need to calculate the forces acting on the object in the water: the upward buoyant force and the downward weight.
We know that the buoyant force is equal to the weight of the fluid displaced by the object. Here, the volume displaced by the object is $100$ liters, which we need to convert to SI units of volume, $m^3$, as $1\,{\rm L}=10^{-3}\,m^3$.
Using the buoyant force formula, we get \begin{align*} F_b&=\rho_{water}\times V_{dis}\times g\\&=(1000)(100\times 10^{-3})(10)\\&=1000\quad {\rm N}\end{align*} The weight of the object, directed downward, is given by $W=mg=1500\,{\rm N}$. Applying Newton’s second law, we find the net force on the object: \[F_{net}=1000\uparrow-1500\downarrow=-500\downarrow\,{\rm N}\] Since weight is greater than the upward buoyant force, the object will sink.
Example (7): A raft has a volume of 6 cubic meters and two-thirds of its volume is submerged in seawater with a density of $1025\,{\rm kg/m^3}$. What is the buoyant force on the raft?
Solution: We can use the buoyant force equation $F_B=\rho V_{dis}g$, where $V_{dis}$ is the amount of the volume of the object under the fluid's level and $\rho$ is the density of the surrounding fluid. \begin{align*} F_B&=\rho V_{dis} g\\ &=(1025)\left(\frac {2}{3} 6\right)(9.8)\\&=40180\quad {\rm N}\end{align*}
Summary:
This article explained how to use the buoyant force equation, which states that the buoyant force is equal to the weight of the fluid displaced by the object.
The article also provided examples of how to apply the equation to different situations, such as finding the volume, weight, or net force of an object in a fluid.
The article used a problem-solving approach to illustrate the steps and calculations involved in each example.
Author: Ali Nemati
Page Created: 1/31/2021
Last Update: Feb 2, 2024
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
