Magnetic Field: Solved Problems for grade 12 and AP Physics
On this page, some Problems on magnetic fields for high school and colleges are solved. Each section is separated for easier reading.
Magnetic Field Problems: Force on a single Moving Charge
Problem (1): A proton moves with a speed of $2\times 10^6 \,\rm m/s$ at an angle of $30^\circ$ with the direction of a magnetic field of $0.2\,\rm T$ in the negative $y$-direction.
(a) What is the magnitude and direction of the magnetic force on the proton?
(b) What acceleration does undergo by the proton?
Solution: The magnitude of the magnetic force on a single charge moving at speed of $v$ in a uniform magnetic field of $B$ is determined by the formula $F=qvB\sin \theta$ where $\theta$ is the angle between velocity and magnetic field. $q$ is also the magnitude of the charge, which in this case is $q=1.6\times 10^{-19}\,\rm C$.
(a) Substituting all numerical values into the above equation, we have \begin{align*} F&=qvB\sin\theta \\\\ &=(1.6\times 10^{-19})(2\times 10^6)(0.3) \sin 30^\circ \\\\ &=4.8\times 10^{-14}\,\rm N \end{align*} An extremely small force. This was the magnitude of the magnetic force. To find the direction of the magnetic force on a positive moving charge, we should use the right-hand rule.
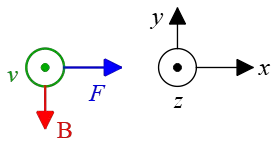
First, identify the directions of $\vec{B}$ and $\vec{v}$ as illustrated in the figure below. Now, according to this rule, put your right fingers along the direction of the charge's velocity $\vec{v}$, then curl your fingers toward the magnetic field $\vec{B}$ through the smaller angle. As a result, your thumb will point in the direction of the magnetic force $\vec{F}$ exerted on the positive charge.
In this case, the thumb points out of the page $\odot$.
(b) Applying Newton's second law, $F=ma$ and solving for $a$ gives \[a=\frac{F}{m}=\frac{4.8\times 10^{-14}}{1.67\times 10^{-27}}=2.87\times 10^{13}\,\rm \frac{m}{s^2}\] Although the magnetic force exerted on the proton was quite small, it experiences a huge acceleration since its mass is also extremely small.
Problem (2): An electron experiences a force of $3.5\times 10^{-15}\,\rm N$ when moving at an angle of $37^\circ$ with the direction of a magnetic field of $2.5\times 10^{-3}\,\rm T$. How fast was the electron?
Solution: Again, the magnitude of the magnetic force exerted by a uniform magnetic field $B$ on a charged particle moving at $v$ with an angle of $\theta$ relative to the $\vec{B}$ is found to be $F=qvB\sin\theta$. Substituting the numerical values into it and solving for $v$, gives \begin{align*} v&=\frac{F}{qB\sin\theta} \\\\ &=\frac{3.5\times 10^{-15}}{(1.6\times 10^{-19})(2.5\times 10^{-3})\sin 37^\circ} \\\\ &=13.7\times 10^6\quad\rm m/s \end{align*} Note that in this formula, only the magnitude of the electric charge is included not its sign. The sign of charge determines the direction of the magnetic force on it.
Problem (3): In the following diagrams, find the direction of the magnetic force on a negative charge. ($\otimes$ and $\odot$ indicate the directions into and out of the page, respectively.)
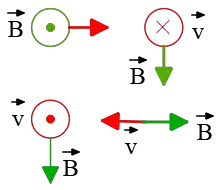
Solution: Notice that in this magnetic field Problem, the charge is negative, so the right-hand rule must be applied with caution. According to this rule, put outstretched fingers of your right hand along the direction of the velocity $\vec{v}$ and curl them toward the magnetic field vector $\vec{B}$ through the smaller angle between them. In this case, your thumb points in the direction of the force.
This instruction is only for positive charges. If the charge was negative, simply reverse the direction of the force.
By doing so, the correct force direction on each diagram is shown below. The blue dotted arrows show the force direction if the charge had been positive.
In the right lower diagram the angle between $\vec{B}$ and $\vec{v}$ is $\theta=180^\circ$, so $\sin \theta=0$, and no force is applied to the particle, $F=0$.
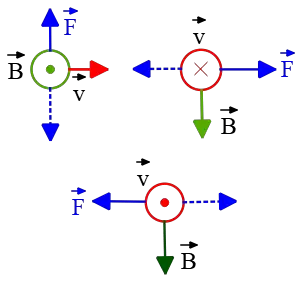
Problem (4): In each of the following diagrams, a charge is shown that enters a region of a uniform magnetic field. Determine the direction of the magnetic force on the charge? (The green arrow shows the direction of $\vec{v}$, $\otimes$ and $\odot$ also represent into and out of the plane of the page, respectively.)
Solution: Place your right-hand fingers in the direction of the velocity $v$ and curl them toward the direction of the magnetic field $B$. The direction of the thumb is in the direction of the force. Note that $\otimes$ and $\odot$ represent vectors pointing into the page and out of the page, respectively.
In the left lower diagram the angle $\theta=180^\circ$, so $\sin 180^\circ=0$, and the force is zero. Pay attention to the sign of the electric charge. For a negative charge, the force direction obtained by the right-hand rule must be reversed.
Problem (5): A proton traveling with a speed of $7.5\times 10^6\,\rm m/s$ enters a uniform external magnetic field of strength $45\,\rm T$ at an angle of $45^\circ$.
(a) What will be the magnetic force acting on the proton?
(b) Draw the direction of the applied force as it moves through the magnetic field. 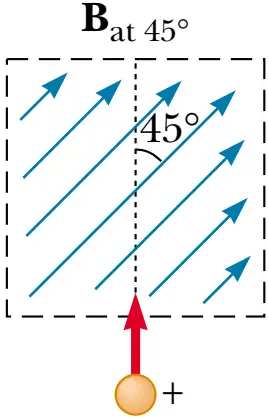
Solution: (a) Substituting all known values into the following formula and solve for $F$.\begin{align*} F&=qvB\sin\theta \\ &=(1.6\times 10^{-19})(7.5\times 10^6)(45) \sin 45^\circ \\ &=3.8\times 10^{-11}\,\rm N \end{align*}
(b) The right-hand rule gives us the direction of the magnetic force into the plane of the page, $\otimes$. Place the fingers of your right hand along the velocity vector (red arrow) and rotate them toward the magnetic field. As a result, your thumb, which shows the direction of the force, points into the page, $\otimes$.
Problem (6): An alpha particle moving at a speed of $2\times 10^7 \,\rm m/s$ toward the positive $z$-direction perpendicularly enters a uniform magnetic field $\vec{B}$ and experiences an acceleration of $1.0\times 10^{13}\,\rm m/s^2$ in the positive $x$-direction. Find the magnitude and direction of the magnetic field?
Solution: The mass of an alpha particle is four times $m_{\alpha}=4m_p$ and its charge is twice $q_{\alpha}=2e$ that of a proton.
The alpha particle's velocity is given as $\vec{v}=2\times 10^7\, (+\hat{k})\quad \rm m/s$.
In this magnetic field Problem, the magnitude and direction of the acceleration acquired by the alpha particle was given. We can use these information to find the magnitude and direction of the applied force to it as below \begin{align*} F&=m_{\alpha}a \\\\ &=(4)(1.67\times 10^{-27})(1.0\times 10^{13}) \\\\ &=6.68\times 10^{-14}\quad \rm N \end{align*} This force directed toward the positive $x$-direction, i.e., $+\hat{i}$, in the same direction of the acceleration.
As you can see, in the following diagram the angle between $\vec{v}$ and $\vec{B}$ is $90^\circ$, so $\sin \theta=1$.
After collecting all these the given information, use the magnetic force formula, $F=qvB\sin\theta$, and solve for $B$ to find the unknown magnitude of the magnetic field \begin{align*} B&=\frac{F}{qv\sin\theta}\\\\ &=\frac{6.68\times 10^{-14}}{(2)(1.6\times 10^{-19}) (2\times 10^7)} \\\\ &=0.01\quad \rm T\end{align*} Now, apply the right-hand rule for a positive charge to find the direction of $\vec{B}$. Here, we choose a coordinate system in which out of the page indicates the positive $z$-direction.
Hold your right hand so that the four fingers point in the $\vec{v}$ (out of the page) and the thumb points toward the $\vec{F}$ (to the right). In this situation, your palm faces in the direction of the magnetic field (up the page).
Problem (7): An electron with a kinetic energy of $1.5\,\rm keV$ perpendicularly enters a $0.02-\rm T$ magnetic field. Determine the radius of its path as it moves through this uniform field?
Solution: First note that $\rm keV$ is a unit of energy in the subatomic level that converts into the usual units of energy, the joules, as below \begin{align*} \rm 1\,keV &=1\times 10^3 \times (1.6\times 10^{-19}) \,J \\ &=1.6\times 10^{-16}\,J\end{align*} By knowing the kinetic energy $K=\frac 12 mv^2$, we can find the particle's velocity as below \begin{align*} v&=\sqrt{\frac{2K}{m}} \\\\ &=\sqrt{\frac{2(1.5)(1.6\times 10^{-16})}{9.11\times 10^{-31}}} \\\\&=2.3\times 10^7\,\rm m/s \end{align*} When a charged particle enters a region of uniform magnetic field at right angle with a speed of $v$, the magnetic field forces it to move in a circular path of radius $r$. This force, whose magnitude is found by $qvB\sin\theta$, serves as a centripetal force radially toward the center of the circle. As we learned in the circular motion Problems section, the acceleration that the object acquire is $a_c=\frac{mv^2}{r}$. Consequently, we have \begin{gather*} F=ma_c \\\\ qvB\sin 90^\circ=\frac{mv^2}{r} \\\\ \Rightarrow \quad r=\frac{mv}{qB} \end{gather*} It is better to memorize this important formula. It always gives the radius of a charged particle moving through a uniform $\vec{B}$ perpendicularly.
Hence, the value of radius is obtained as follows \begin{align*} r&=\frac{(9.11\times 10^{-31})(2.3\times 10^7)}{(1.6\times 10^{-19})(0.02)} \\\\ &=0.65\times 10^{-2}\,\rm m\end{align*} Therefore, this electron having such energy when enters a $0.02\,\rm T$ field bends around a circle of radius $0.65\,\rm mm$.
For more information about this bending, refer to the helical motion in a magnetic field.
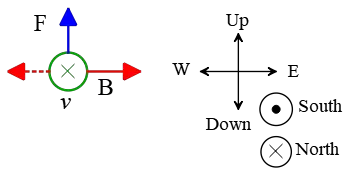
Problem (8): An electron undergoes the greatest force of magnitude $3.2\times 10^{-13}\,\rm N$, vertically upward, when it travels northward at a speed of $5\times 10^6 \,\rm m/s$ in a uniform magnetic field of unknown strength. What is the magnitude and direction of the magnetic field?
Solution: in all magnetic field questions, the greatest force occurs when the angle between $\vec{v}$ and $\vec{B}$ is $90^\circ$. In this case, $\sin\theta=1$. By solving the equation $F=qvB\sin\theta$ for $B$ and substituting the numbers into it, we get \begin{align*} B&=\frac{F}{qv} \\\\ &=\frac{3.2\times 10^{-13}}{(1.6\times 10^{-19})(5\times 10^6)} \\\\ &=0.4\,\rm T \end{align*} To find the direction of the field, first of all, set a coordinate system and specify all the directions on it as below. In this standard coordinate system, used when geographical direction included in the Problem, we assume north and south directions as into $\otimes$ and out of the page $\odot$, respectively.
Place the four fingers of your right hand in the direction of velocity $\vec{v}$ so that your thumb points to the force direction. In this case, your palm faces toward the magnetic field. This is the right-hand rule for a positive charge.
Doing so, your palm will be toward the left (or west) but the electric charge of the electron is negative so you must reverse that direction (which is shown as a red dotted arrow) to find the correct direction of the field.
Problem (9): A proton traveling with a speed of $2.4\times 10^6\,\rm m/s$ through a uniform magnetic field of strength $2.5\,\rm T$ experiences a force of magnitude $4.8\times 10^{-13}\,\rm N$. At what angle does the electron enter the field?
Solution: here, the unknown is the angle between $\vec{v}$ and $\vec{B}$. Applying the magnetic force formula, $F=qvB\sin\theta$, and solving for the unknown angle $\theta$ gives \begin{align*} \sin\theta &=\frac{F}{qvB} \\\\ &=\frac{4.8\times 10^{-13}}{(1.6\times 10^{-19})(2.4\times 10^6)(2.5)} \\\\&= 0.5 \end{align*} Taking the inverse sine of both sides, gives us the desired angle \[\theta=30^\circ\]
Problem (10): The path of a negatively charged particle traveling through a magnetic field is shown in the figure below. What is the direction of the $\vec{B}$ field?
Solution:
Magnetic Field Problems: Force on Electric Current
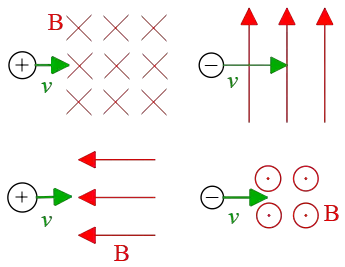
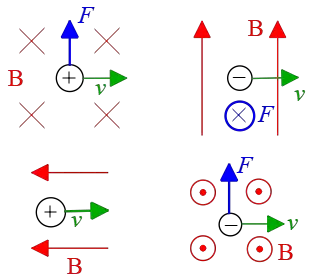
Problem (11): In each of the following diagrams, a current-carrying wire is shown into a uniform external magnetic field. Find the direction of the magnetic force for each diagram.
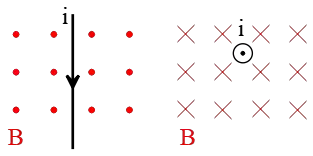
Solution: Place outstretched fingers of your right hand along the direction of the current. For the left diagram, your fingers must point down the page. Now, curl them toward the magnetic field $B$ which is out of the plane of the page. As a result, your thumbs, which represent the force, points to the left.
For the right diagram, there is an interesting point. If look closely, the current is out of the page and the field is into the page, so the angle between them is $180^\circ$ and we know that $\sin 180^\circ=0$. Consequently, there is no force acting on this wire.
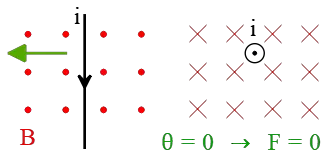
Problem (12): Find the magnitude of the force per meter exerted on a straight wire carrying a current of $3.5\,\rm A$ through a magnetic field of $0.85\,\rm T$ when
(a) it is placed perpendicular to the $\vec{B}$.
(b) it makes an angle of $37^\circ$ with the field.
Solution: When a straight wire of length $\ell$ carrying a current $i$ passes through a uniform external magnetic field $\vec{B}$, it experiences a force of magnitude $F=i\ell B\sin \theta$ where $\theta$ is the angle between the direction of the current and $\vec{B}$.
The force ''per meter'' means the force acted on one meter of the wire, so $\ell=1\,\rm m$.
(a) In this case, we have $\theta=90^\circ$, so $\sin\theta=1$. Thus, the magnitude of the force is found to be \begin{align*} F&=i\ell B\sin\theta \\&=(3.5)(1)(0.85) \\&=2.975\quad \rm N \end{align*}
(b) Similarly, we have \begin{align*} F&=i\ell B\sin\theta \\&=(3.5)(1)(0.85) \sin 37^\circ \\&=1.785\quad \rm N \end{align*}
Problem (13): A straight wire carrying a current of $4\,\rm A$ is placed perpendicularly in a uniform magnetic field of strength $0.45\,\rm T$. What is the magnitude of the magnetic force on a $35-\rm cm$-long section of this wire?
Solution: All the required information to substitute into the magnetic force formula is given. Hence, we have \begin{align*} F&=i\ell B\sin\theta \\&=(4)(0.35)(0.45) \sin 90^\circ \\&=0.63\quad \rm N \end{align*}
Problem (14): An straight section of a wire $0.40\,\rm m$ long carrying a steady current of $2.5\,\rm A$ toward the $+x$ direction lies in a region where a uniform magnetic field of strength $B=1.5\,\rm T$ to the $+z$ direction is present. What is the magnitude and direction of the magnetic force on this section of wire?
Solution: In this magnetic field Problem, the angle between $\vec{B}$ and the direction of the electric current is $90^\circ$, so $\sin\theta=1$. The magnitude of the magnetic force is also determined as below \begin{align*} F&=i\ell B\sin \theta \\ &=(2.5)(0.40)(1.5) \\ &=1.5\quad \rm N\end{align*} To find the direction of the force acting on the wire, do the following:
Point the fingers of your right hand in the direction of the current $i$ and curl them toward the magnetic field direction. Your thumb, then, points in the direction of the magnetic force. This is the right-hand rule for finding the magnetic force on a current-carrying wire in a uniform $\vec{B}$.
Problem (15): At a location where the Earth's magnetic field is $0.5\,\rm G$ from south to north, there is a straight wire of length $2\,\rm m$ that carries a current of $1.5\,\rm A$. In each of the following situations, find the magnitude and direction of the magnetic force exerted on the wire due to the earth's magnetic field?
(a) a current flowing from west to east.
(b) a current flowing vertically upward.
(c) a current flowing north to south.
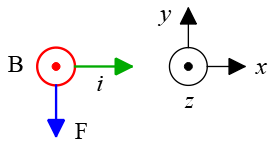
Solution: The magnitude of the magnetic force is obtained by the equation $F=i\ell B\sin\theta$ and its direction is also found by the right-hand rule. To solve such magnetic field Problems, first set up a coordinate system and specify each direction on it as below. In this coordinate system south and north directions are shown by the symbols $\odot$ and $\otimes$ means out of and into the page, respectively.
The Earth's magnetic field is from south to north, which we can imagine as an arrow points into the page, i.e., $\otimes$. The gauss, $\rm G$ is another unit for magnetic field and is related to the tesla by $\rm 1\, G=10^{-4} \, T$.
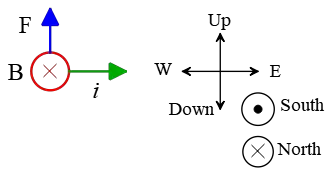
(a) As shown in the figure below, the angle between $\vec{B}$ and the direction of the current is $\theta=90^\circ$, so $\sin\theta=1$. Thus, the force's magnitude is \begin{align*} F&=i\ell B\sin\theta \\&=(1.5)(2)(0.5\times 10^{-4}) \\&=1.5\times 10^{-4}\,\rm N\end{align*} Using the right-hand rule the direction of the force is upward.
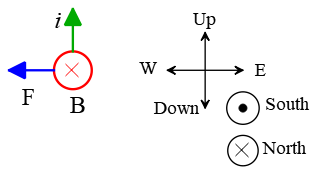
(b) Again, in this case, $\theta=90^\circ$, and the other things have not changed, so the magnitude of the exerted force on the wire is the same as the previous. The direction of the exerted force is also leftward.
(c) The current is north to south which is represented by the symbol $\odot$. On the other hand, the field is south to north, $\otimes$. Thus, the angle between these two vectors is $180^\circ$, and we know that $\sin 180^\circ=0$. Consequently, there is no force on a wire carrying a current in that direction.
Problem (16): In a region of space, a magnetic force per unit length of $0.24\,\rm N/m$ toward the positive $z$-axis exerts on a current of $I=10\,\rm A$ directed along the positive $y$-direction and perpendicular to the magnetic field $\vec{B}$. Determine the magnitude and direction of the magnetic field?
Solution: the magnitude of the magnetic force on a wire of length $\ell$ carrying current $i$ in a uniform external magnetic field $\vec{B}$, is determined by the following formula \[F=i\ell B\sin\theta\] where $\theta$ is the angle between the direction of the current and the direction of the magnetic field. When this angle is $90^\circ$, the magnetic force acted on the wire is maximum.
Here, the maximum ($\theta=90^\circ$) force per unit length was given $F/\ell=0.24\,\rm N/m$. Substituting the given data into the above formula and solving for $B$ gives \begin{align*} B&=\frac{F}{i\ell} \\\\ &=\frac{0.24}{10}\\\\ &=0.024\quad \rm T \end{align*} The right-hand rule gives us the direction of $\vec{B}$.
To find the magnetic force direction on a wire carrying current in a uniform magnetic field, the following version of the right-hand rule must be applied.
Point the fingers of your open right hand in the direction of the current and bend them toward the magnetic field $\vec{B}$. The thumb, then, points in the direction of the magnetic force $\vec{F}$.

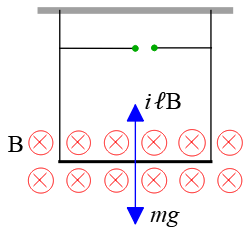
Problem (17): In the following figure, a horizontal conductor of length $30\,\rm cm$ and of mass $25\,\rm g$ is suspended by two thin vertical wires in a uniform external magnetic field of $1.5\,\rm T$ that is directed into the page. The terminals of the battery are unknown. What current and in which direction must it flow through the conductor so that the voltage in the wires is zero?

Solution: When a current establishes in the loop, those two vertical wires have currents in the opposite directions. Using the right-hand rule, we can find that the forces exerted on the left and right vertical wires are equal in magnitude and opposite in directions that lead to canceling each other.
We were asked to make a situation in which the tension in the wires be zero. This holds when the downward conductor's weight force $mg$ is balanced with an upward magnetic force $i\ell B$. Note that, here, the angle between $\vec{B}$ and the wire is $\theta=90^\circ$, so $\sin \theta=1$.
Balancing these two forces acting on the conductor, $i\ell B=mg$, and solving for the unknown current $i$ gives \begin{align*} i&=\frac{mg}{\ell B} \\\\ &=\frac{0.025\times 9.8}{0.30\times 1.5} \\\\&=0.55\,\rm A \end{align*} To find the direction of the current in the conductor, use the right-hand rule. Place the thumb of your right hand upward in the direction of the force $i\ell B$ so that the palm points to the direction of the field which is into the page, $\otimes$. Your four fingers point in the direction of the current that is toward the left.
Magnetic Field Due to a Long Straight Wire
Problem (18): A current of $20\,\rm A$ flows vertically upward in a straight wire. What is the magnitude and direction of the magnetic field due to this long wire at a location $15\,\rm cm$ away and on the left side of the wire?
Solution: The magnitude of the magnetic field due to a long straight wire near to it is found as follows \[B=\frac{\mu_0 I}{2\pi r} \] where $\mu_0=4\pi\times 10^{-7}\,\rm T\cdot m/A$ is called the permeability of free space. Plug in the known values gives \begin{align*} B&=\frac{(4\pi\times 10^{-7})(20)}{2\pi\times 0.15} \\\\ &=2\times 10^{-5}\,\rm T\end{align*} To find the direction of the magnetic field due this long wire, we must use the following version of the right-hand rule:
Grasp the wire in your right hand so that the thumb points in the direction of the current. Now, wrap your four fingers around the wire. This is the direction of the $\vec{B}$.
Doing so, in this case, at the point $P$ on the left side of the wire the fingers will come out of the paper, $\otimes$.
Similarly, on the right side, the four fingers will come into the paper, $\otimes$. These are the directions of the $\vec{B}$ at those points.
Author: Dr. Ali Nemati
Published: 3/2/2022
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
