Uniform Circular Motion Problems with Answers
In the following, some problems on uniform circular motion are provided with detailed answers. These questions on circular motion are beneficial for students in high school and college.
Circular Motion Problems: Kinematic
Problem (1): A 5-kg object moves around a circular track with a radius of 18 cm at a constant speed of 6 m/s. Find
(a) The magnitude and direction of the acceleration of the object.
(b) The net force acting upon the object causing this acceleration.
Solution: When an object moves around a circular path at a constant speed, the only acceleration it experiences is centripetal acceleration or radial acceleration.
This kind of acceleration is always toward the center of the circle, and its magnitude is found by the following formula: \[a_c=\frac{v^2}{r}\] where $v$ is the constant speed with which the object revolves the circle, and $r$ is the radius of the circle.
(a) The track is circular and the speed of the object is constant, so a centripetal acceleration directed toward the center is applied to the object, whose magnitude is as follows \[a_c=\frac{6^2}{0.18\,{\rm m}}=50\,{\rm \frac{m}{s^2}}\] In the figure below, a top view of the motion is sketched.
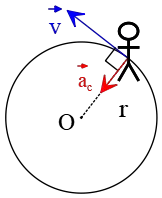
(b) By applying Newton's second law along the direction of the centripetal acceleration, we can find the magnitude of the net force causing the acceleration as follows \[F_{net}=m\frac{v^2}{r}\] Therefore, \[F_{net}=5\times 50=250\quad {\rm N}\]
Note: At each point along the circular path, the instantaneous velocity of the revolving object is tangent to the path. The direction of this velocity changes, but its magnitude remains constant.
Problem (2): On a merry-go-round moving at a speed of 3 m/s, there is a 25-kg child sitting 3 m from the center. Calculate the following:
(a) the centripetal acceleration of the child,
(b) the net horizontal force acting on the child,
(c) compare the above force with the child's weight.
Solution: (a) The child has a circular motion with a centripetal acceleration given by $a_c=v^2/r$, where $v$ is the constant speed of the revolving object. Therefore, we have \[a_c=\frac{3^2}{3}=3\quad {\rm \frac{m}{s^2}}\]
(b) The net force can be found using Newton's second law as $F_{net}=ma_c$, which gives us \[F_{net}=25\times 3=75\quad {\rm N}\] This force is in the same direction as the acceleration, toward the center of the circle.
(c) Weight is calculated as mass times the gravitational acceleration at that place ($g$) or $w=mg$. The ratio between these two forces is \[\frac{F_{net}}{w}=\frac{75}{25\times 10}=0.3\]
Problem (3): A cyclist is moving around a circular path with a radius of 50 m at a speed of 10 m/s.
(a) Find the cyclist's acceleration.
(b) Considering the combined mass of the cyclist and bicycle to be 120 kg, what is the net force applied to them?
Solution: (a) When moving with constant speed around a circular path, the cyclist experiences a radially inward acceleration known as centripetal acceleration. The magnitude of this acceleration can be found using the formula: \[a_c=\frac{v^2}{r}=\frac{10^2}{50}=2\quad {\rm \frac{m}{s^2}}\]
(b) The net force acting on the cyclist and bicycle to keep them moving along the circular track is called the centripetal force. Its magnitude can be determined using Newton's second law: \[F_{net}=ma_c=120\times 2=240\quad N\]
Problem: A particle moves in a uniform circular motion with a radius of 3 cm. The net force radially acting on the object is 30 N. If the mass of the object is 6 kg,
(a) What is centripetal acceleration?
(b) What is the particle's linear speed?
(c) What is the acceleration if the radius is doubled without changing the particle's speed?
(d) What is the acceleration if the angular velocity is doubled without changing the circle's path?
Solution: Centripetal acceleration is defined as the acceleration that an object experiences when it turns around a circular path. This acceleration points radially inward toward the center of the circular path and is related to the corresponding centripetal force, $F_c$, by the following formula \[F_c=ma_c=m\frac{v^2}{r}\] where $r$ is the radius of the circular path and $v$ is the linear speed of the revolving object.
(a) According to the above explanation, $a_c$ can be found as \begin{gather*} F_c=ma_c \\ 30=6\times a_c \\ \Rightarrow a_c=5\,\rm m/s^2\end{gather*}
(b) Centripetal acceleration and linear speed are related by $a_c= \frac{v^2}{r}$. Substituting the numerical values into that and solving for $v$ get \begin{gather*} a_c=\frac{v^2}{r} \\\\ 5=\frac{v^2}{0.03} \\\\ \rightarrow v^2=0.15 \\\\ \Rightarrow \boxed{v=\sqrt{0.15}\,\rm m/s} \end{gather*}
(c) According to the centripetal acceleration formula, $a_c=\frac{v^2}{r}$, acceleration is inversely proportional to the radius of the circular path, $a_c\propto 1/r$. Therefore, we have \begin{gather*} \frac{a_c}{a'_c}=\frac{r'}{r} \\\\ \frac{5}{a'_c}=\frac{2\times 3}{3} \\\\ \Rightarrow \boxed{a'_c=2.5\,\rm m/s^2} \end{gather*}
(d) We can also express the centripetal acceleration $a_c$ in terms of the angular velocity $\omega$ using formula \[a_c=r\omega^2\] Substituting the given numerical values into that equation gives \begin{gather*} a_c=r\omega^2 \\ 5=0.03 \times \omega^2 \\\\ \omega=\sqrt{\frac{5}{0.03}}\ \rm rad/s \end{gather*}
Problem (4): A jet plane is maneuvering in a circular path with a radius of 5.5 km at a constant speed of 2160 km/h. What is the acceleration of the plane in g's?
Solution: This is a circular motion problem with constant speed, so the only acceleration is due to centripetal acceleration.
Because we are going to compare this acceleration with gravitational acceleration, $g=9.8\,{\rm m/s^2}$, it is better to first convert all units into SI units.
This conversion for constant speed is as follows \[\rm{1\,\frac{km}{h}}=\rm{\frac{1000\,m}{3600\,s}}=\frac{10}{36} {\rm \frac{m}{s}}\] So, 2160 km/h in SI units is converted as \[2160\times \frac{10}{36}=600\quad {\rm \frac{m}{s}}\] Therefore, the magnitude of the centripetal acceleration is \[a_c=\frac{v^2}{r}=\frac{600^2}{5000\,m}=72\quad {\rm \frac{m}{s^2}}\] To compare it with gravity, we should divide it by $g$ \[\frac{a_c}{g}=\frac{72}{9.8}=7.35\] Thus, this acceleration is about seven times greater than the gravitational acceleration, $a_c=7.35\,g$.
Problem (5): A race car is traveling around a circular path with a radius of 400 m at a speed of 50 m/s. Find the centripetal acceleration of the car.
Solution: In a circular motion with constant speed, the centripetal acceleration is $a_c=v^2/r$. Therefore, substituting the numerical values into this equation, we have \[a_c=\frac{v^2}{r}=\frac{50^2}{400}=6.25\,{\rm \frac{m}{s^2}}\] This acceleration is toward the center of the circle.
Problem (6): A crankshaft of radius 8 cm rotates at 2400 rpm (revolutions per minute). What is the speed of a point at its surface?
Solution: The aim of this circular motion problem is the conversion of rpm into SI units of speed (m/s), which is done as below: \begin{align*} 1 \frac{rev}{minute}&=\frac{\text{circle's circumference}}{60\,\text{seconds}}\\\\&=\frac{2\pi r}{60}\\\\&=\frac{\pi r}{30}\end{align*} Hence, to convert rpm to $m/s$, we can use the following conversion ratio \[ \rm{1\,rpm}=\frac{\pi r}{30}\,{\rm \frac ms}\] In this problem, the circular motion has a radius of $r=0.08\,{\rm m}$ and an angular speed of 2400 rpm, so we get \[2400\,{\rm rpm}=2400\times\frac{\pi(0.08)}{30}=20.1\,{\rm \frac ms}\]
Problem (7): A 20-kg child sits in a cart to which a 2-m rope is attached. The rope is tied to a motor that rotates the cart. At the instant that the tension in the rope is 100 N, how many revolutions per minute does the cart make?
Solution: This circular motion question aims to find the method of conversion of $m/s$ into $\rm rpm$.
The child revolves in a circular path, so the net centripetal force it experiences is determined by $F_c=\frac{mv^2}{r}$.
First, use the above equation and solve for the constant speed $v$ as below \[v=\sqrt{\frac{rF_c}{m}}=\sqrt{\frac{2\times 100}{20}}=\sqrt{10}\,{\rm \frac ms}\] Next, convert the above linear speed in ($\rm \frac ms$) into angular speed in revolutions per minute ($\rm rpm$).
The simple relation between the two speeds is as $v=r\omega$, where $\omega$ is the angular speed measured in radians per second. \[\omega=\frac{v}{r}=\frac{\sqrt{10}}{2} \,{\rm \frac {rad}{s}}\] Next, as shown below, convert $\rm \frac{rad}{s}$ into $\rm rpm$ \[ \frac{1\,rad}{s}=\frac{\frac{1}{2\pi}\,rev}{\frac {1}{60}\,min}=\frac {30}{\pi}\, \rm rpm\] In the above, we used this fact that each revolution around a circle is equal to $2\pi$ radians. As a result, we have \[\sqrt{10}\,{\rm \frac ms}=\sqrt{10}\left(\frac{30}{\pi}\right)\,{\rm rpm}=30.2\,{\rm rpm}\] Hence, the cart makes about 30 revolutions per minute.
Problem (8): A radially inward constant force of 300 N is exerted on a 2-kg ball as it revolves around a circle of radius of 85 cm. What is the speed of the ball?
Solution: The ball revolves around a circle, so the only radially inward force acting upon the object is the centripetal force, whose magnitude is $F_c=mv^2/r$. Therefore, putting the numerical values into it and solving for the unknown $v$, we have \[v=\sqrt{\frac{rF_c}{m}}=\sqrt{\frac{0.85\times 300}{2}}=11.3\,{\rm \frac{m}{s}}\]
Problem (9): A 35-kg child makes a turn that is a portion of a circle with a radius of 12 meters. She covers one-quarter of the circular path in 1.6 seconds. Determine the speed, acceleration, and net force applied to the child.
Solution: The child turns one-quarter of a circle in $1.6$ seconds.
Using the definition of speed, as distance traveled divided by time elapsed, we can find its speed.
But here, the distance traveled is the circumference of one-quarter of a circle of radius $12$ meters, so $L=\frac 14 (2\pi r)=\frac{\pi r}{2}$. \begin{align*} speed&=\frac{distance}{\text{time elapsed}}\\\\&=\frac{\pi r/2}{time}\\\\&=\frac{\pi\times (12/2)}{1.6}\\\\&=11.8\quad {\rm m/s}\end{align*} Because the child is moving around a portion of a circular path, centripetal acceleration is applied to the child, whose magnitude is $a_c=v^2/r$. \[a_c=\frac{v^2}{r}=\frac{(11.8)^2}{12}=11.6\quad{\rm \frac{m}{s^2}}\] The net force is also found using Newton's second law of motion as $F_{net}=ma_c$. \[F_{net}=ma_c=35\times 11.6=406\quad {\rm N}\]
Problem (10): A ball of mass 2 kg is attached to a rope having a breaking strength of 1500 N and is whirled around a horizontal circle with a radius of 85 cm. Calculate the maximum speed that the ball can have.
Solution: There is a circular motion, so the only radially inward force that acted upon the ball is a centripetal force whose magnitude is $F_c=mv^2/r$ where $r$ is the radius of the circular path.
Putting everything into this equation and solving for the unknown velocity, we have \[v=\sqrt{\frac{rF_c}{m}}=\sqrt{\frac{0.85\times 1500}{2}}=25.25\,{\rm \frac{m}{s}}\]
The following circular motion questions are helpful for the AP physics exam.
Problem (11): The speed of a 515-kg roller-coaster at the bottom of a loop of radius 10 m is 20 m/s. Find the net vertical force pushing up on the object at this point of the circular path.
Solution: Note that because of gravity, the speed of the object changes at each point of the track, so the object is not undergoing uniform circular motion. Nonetheless, we can use the centripetal acceleration formula to find the velocity at each point along the circle.
At the bottom, two forces are applied to the object: the downward force of gravity, $mg$, and the upward tension force. The resultant of these two forces makes a centripetal acceleration toward the center of the circle.
Applying Newton's second law in this direction (by choosing upward as the positive direction since acceleration at this point is upward), we have \begin{align*} F_c-mg&=\frac{mv^2}{r}\\\\ \Rightarrow F_c &=mg+\frac{mv^2}{r}\\\\&=(515)(10)+\frac{515\times (20)^2}{10}\\\\&=25750\quad {\rm N}\end{align*}
Problem (12): A 2000-kg car is moving around a curve with a radius of 200 m at a speed of 25 m/s. Calculate
(a) The centripetal acceleration of the car.
(b) The force causing this kind of acceleration.
(c) The minimum coefficient of static friction between the tires and the surface of the road guarantees a safe turning.
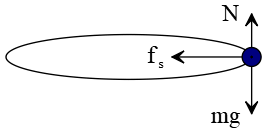
Solution: The free-body diagram below (side view) shows all forces acting on the car.
(a) Centripetal acceleration is found by the following formula \[a_c=\frac{v^2}{r}=\frac{25^2}{200}=3.125\quad {\rm \frac{m}{s^2}}\]
(b) The force along this direction is found using Newton's second law of motion as below \[F_c=ma_c=2000\times 3.125=6250\quad {\rm N}\]
(c) When a car turns a curve, it experiences a centripetal acceleration toward the center of the curve. The force causing this acceleration for a car around a curve is static friction force.
If the static friction force is not great enough, the car will skid out of the curve and follow a nearly straight line. In this situation, the static friction must be balanced with the force needed to produce the given centripetal acceleration.
On the other hand, recall that the maximum value of static friction force is given by $f_{s, max}=\mu_s N$, where $N$ is the normal force on the car, which is equal to the weight $mg$ (only for flat circular tracks). Thus, \begin{align*} \mu_s (mg)&=\frac{mv^2}{r}\\\\ \Rightarrow \mu_s&=\frac{v^2}{rg}\\\\&=\frac{25^2}{200\times 9.8}\\\\&=0.32\end{align*} Therefore, the car can make a safe round if the coefficient of static friction is greater than this value.
Practice these questions to understand friction force:
Problems on the coefficient of friction
Problem (13): A 1500-kg car moves around a flat circular track with a radius of 30 m. The coefficient of friction between the car's tires and the road is 0.3. Find the maximum speed at which the car turns the track.
Solution: The static friction between the car's tires and the road provides the force required for turning the car around the circular track.
The maximum value of the static friction force formula is $f_{s, max}=\mu_s N$, where $N$ is the force exerted on the car from the surface of the road, which is called the normal force. By setting Newton's second law in the vertical direction to zero (because the car does not fly!), we can find the normal force as below \[N-mg=0 \Rightarrow N=mg\] Next, apply Newton's second law of motion again to the radial direction.
Because the car moves around a curve, it experiences centripetal acceleration provided by static friction. Thus, \begin{align*} f_{s,max}&=\frac{mv^2}r \\ \\\mu_s (mg)&=\frac{mv^2}r\\\\ \Rightarrow\quad v&=\sqrt{r\mu_s g}\\\\&=\sqrt{30\times (0.3)\times 9.8}\\\\&=9.4\quad {\rm \frac ms}\end{align*}
Problem (14): A car is to turn a curve track with a radius of 120 m at a speed of 85 km/h. How large must the coefficient of static friction be between the car's tire and the road to maintain safe travel?
Solution: The forces on the car are the downward gravity force, $mg$, the normal force $N$ exerted upward by the road, and the static friction force due to the road. All these forces are shown in the free-body diagram below.
In the vertical direction, there is no acceleration. By applying Newton's second law, we find that the gravity force is equal to the normal force. \[\Sigma F_y=0 \rightarrow N-mg=0 \Rightarrow N=mg\] In the radial direction, the net force required to keep the car on a circular path is found using the centripetal force formula, $F_c=\frac{mv^2}{r}$.
This force must be balanced with the static friction force to guarantee a safe turn. Thus, the required condition for not skidding on the curve is as follows \[F_c=f_{s,max}\] where $f_{s,max}=\mu_s N$ is the maximum value of the friction force. Therefore, \begin{align*} \frac{mv^2}{r}&=\mu_s (mg) \\\\\Rightarrow \quad \mu_s&=\frac{v^2}{r\,g}\\\\&=\frac{(23.6)^2}{10\times 120}\\\\&=0.4\end{align*}
In the above, we converted ``km/h'' to ``m/s'' as below \[ 85\,{\rm \frac{km}{h}}=85\,\rm{\left(\frac{1000\,m}{3600\,s}\right)}=23.6\,{\rm \frac ms}\]
Problem (15): A 2-kg bucket at the end of a rope is circulated in a vertical plane with a radius of 1.5 m. The tension of the rope at the lowest point of the path is 30 N. Calculate
(a) The speed of the bucket.
(b) How fast must the bucket at the top of the path move so that the rope does not go slack?
Solution: The gravity force, $mg$, and the tension in the rope are exerted on the bucket, which is moving in a circular motion. A free-body diagram shows these forces below.
(a) Apply Newton's second law at the lowest point of the path to find the equation governing that point.
We choose the upward direction as positive because it is in the direction of centripetal acceleration (radially inward). \begin{align*} T-mg&=\frac{mv^2}{r}\\\\ 30-2(10)&=\frac{2\times v^2}{1.5}\\\\ 10\times 1.5&=2v^2\\\\\Rightarrow v&=2.8\,{\rm \frac ms}\end{align*}
(b) The sum of the forces at the highest point of the circle, using Newton's second law, is written as below (down is considered as positive) \begin{align*} T+mg&=\frac{mv^2}r\\\\ \Rightarrow v&= \sqrt{\frac{r(T+mg)}{m}}\end{align*} If we set $T=0$ in the above, the rope is on the verge of going slack. Therefore, \[v= \sqrt{\frac{r(T+mg)}{m}}= \sqrt{\frac{(1.5)(0+2\times 10)}{2}}=3.8\,{\rm \frac ms}\]
Problem (16): A jet plane moves around a vertical circular loop. Its speed at the lowest point of the circle is 950 km/h. Find the minimum radius of the circular path so that the (centripetal) acceleration exerted on it does not exceed 5 g's.
Solution: The jet moves around a circular path and must experience centripetal acceleration. Set this acceleration to $5g$ and solve for $r$. Thus, we have \begin{align*} a_c&=5g \\\\\frac{v^2}{r}&=5g \\\\\Rightarrow r&=\frac{v^2}{5g}\\\\&=\frac{(950\,\frac {km}{h})\left(\frac{1000\,m}{3600\,s}\right)}{5(9.8)}\\\\&=1421\,{\rm m}\end{align*}
(b) The weight of the pilot is 75 kg. What is its apparent weight at the bottom and top of the circle?
The apparent weight is equal to the net force on the pilot in the plane. Two forces act on the pilot. One is the downward gravity force, $mg$, and the other is the upward normal force at the lowest point of the circular path. These two forces acting on the pilot are shown in the free-body diagram below.
The vector sum of these two forces provides the centripetal acceleration around the curved path. \[\Sigma F_r=N-mg=m\frac{v^2}{r}\] where we have chosen up as the direction of the acceleration (radially inward) at this point, as the positive direction. Therefore, \begin{align*} N&=mg+mv^{2}/r\\ &=mg+m(5g)\\&=6mg\\&=6(75)(9.8)\\&=4410\,{\rm N}\end{align*} In all such vertical circular problems, the normal force is the apparent weight.
Problem (17): The radius of a highway curve banked at an angle of $13^\circ$ is 75 m. At what speed can a car make a turn this curve without the help of friction?
Solution: To solve this problem, we can use the concept of centripetal force. When a car turns on a curved road, the centripetal force required to keep it moving in a circle is provided by the friction between the tires and the road surface.
However, in this case, we are asked to find the speed at which the car can make the turn without relying on friction. This means that there is no horizontal component of friction acting on the car.
Two real forces act on the car: the force of gravity, and the normal force $\vec{N}$. Establish a coordinate system so that the centripetal force lies in the radial direction as depicted in the figure below.
The vertical component of the normal force provides the necessary centripetal force in this situation. The normal force can be resolved into two components.
The $y$-component of the normal force cancels out with gravity, while the radial component provides the centripetal force. Write Newton's second law along the $y$-direction: \[N\cos\theta=mg \] On the other hand, the radial component of the normal force, $N\sin\theta$, is the same as the centripetal force, which is given by: \begin{gather*} F_{\text{centripetal}} = N\sin\theta \\\\ \frac{mv^2}{r}=N\sin\theta \end{gather*} Dividing these two last expressions, we get a relation as follows \[\tan\theta=\frac{v^2}{rg}\] Rearranging that, solving for $v$ and substituting the given numerical values into it yields \begin{align*} v&=\sqrt{rg\tan\theta}\\\\ &=\sqrt{75\times 9.8\times \tan 13^\circ} \\\\ &=13.02\,\rm m/s\end{align*} Therefore, the car can make the turn on this curve without the help of friction at a speed of approximately 13 m/s.
Problem (18): An electron is moving in a circular track with a radius of 2 mm at a speed of $2\times 10^{6}\,{\rm m/s}$. Find
(a) The period of the revolutions;
(b) The centripetal acceleration experienced by the electron.
Solution: (a) This electron, every 1 second covers a distance of $2\times 10^6 \,{\rm m/s}$ which is the circumference of the circle.
Recall that the circumference of a circle of radius $r$ is $2\pi r$, thus we must first find how many numbers the electron revolves around this circular track. \[L=N(2\pi r) \Rightarrow N=\frac{L}{2\pi}\] On the other hand, the period is the time it takes the electron to make one revolution in one second. According to this definition, the period of an object with $N$ revolutions is obtained as \[T=\frac{1}{N}=\frac{2\pi r}{L}\] Using this formula, we can find the period of this electron \[T=\frac{2\pi\times (0.002)}{2\times 10^6}=6.3\times 10^{-9}\,{\rm s}\] Hence, the period of the electron is about $6\,{\rm ns}$.
(b) The electron moves along a circular motion whose centripetal acceleration is computed as below \[a_c=\frac{v^2}{r}=\frac{(2\times 10^6)^2}{0.002}=10^9\quad {\rm \frac {m}{s^2}}\]
Problem (19): A 0.45-kg ball is fastened to a rope and is swung in a horizontal plane (without friction) around a circle of radius 1.3 m. When the tension in the rope exceeds 75 N, the rope is broken. What is the maximum speed the ball can have at this point?
Solution: In this circular motion problem, the only force causing the centripetal acceleration is tension in the rope. By applying the centripetal force formula, $F_c=mv^2/r$, and solving for unknown speed $v$, we get \[v=\sqrt{\frac{rF_c}{m}}=\sqrt{\frac{1.3\times 75}{0.45}}=14.7\,{\rm \frac ms}\]
Problem (20): How fast must a centrifuge revolve if a point particle located 5 cm from its axis of rotation is to experience a centripetal acceleration of 100,000 g's?
Solution: The particle in a centrifuge has a circular motion with a constant speed. Solving for $v$ in the centripetal acceleration, $a_c=v^2/r$, we have \[v=\sqrt{ra_c}=\sqrt{0.05\times 100,000}=32\,{\rm \frac ms}\]
Problem (21): What is the acceleration of a stone attached to the end of a 2-m-long rope revolving at 45 revolutions per minute (rpm)?
Solution: The stone has a circular motion with the given constant speed. In this problem, the speed of a revolving object is given in rpm or angular speed.
To use the centripetal acceleration formula, $a_c=v^2/r$, we need speed in $m/s$. To convert angular speed (rpm) into linear speed (m/s), we proceed as below formula \[v(m/s)=r\times \frac{rpm \times 2\pi}{60}\] Therefore, an angular speed of "45 rpm" is converted into "m/s" as below \[v=2\times \frac{2\pi \times 45}{60}=9.5 \,{\rm m/s}\] Now, we can plug this value into the centripetal acceleration formula \[a_c=\frac{v^2}{r}=\frac{(9.5)^2}{2}=45.1\quad {\rm \frac {m}{s^2}}\]
Problem (22): A car moves along a curved path as shown in the following figure. When the car reaches the bottom of the track, find
(a) the normal force exerted on the car and
(b) the effective weight (apparent weight) of the car.
Solution: At the bottom of the track, two forces act on the car. The downward gravity force, $mg$, and the upward force due to the contact between the car and the surface, which is known as the normal force, $N$.
The car rounds a curve, so it experiences a centripetal force $F_c$ radially inward in the same direction as centripetal acceleration. At the bottom of the track, this force is directed upward.
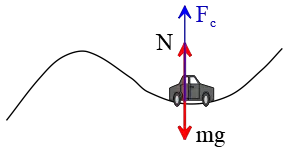
It is better to choose this direction as positive and apply Newton's second law along this direction as below: \begin{gather*} N-mg=\frac{mv^2}{r} \\\\ \Rightarrow N=mg+\frac{mv^2}{r} \end{gather*}
Problem (23): A centripetal force $F$ is exerted on an object moving around a circular track with a constant speed $v$. If the speed of the object is tripled and the radius of the track is quadrupled, what happens to the centripetal force?
Solution: The centripetal force in a circular motion is given by the equation $F_c=\frac{mv^2}{r}$. As you can see, this kind of force is proportional directly to the speed of the object and inversely to the radius of the curved path. Therefore, \begin{align*} \frac{F_2}{F_1}&=\left(\frac{v_2}{v_1}\right)^2 \frac{r_1}{r_2}\\\\&=\left(\frac{3v_1}{v_1}\right)^2 \frac{r_1}{4r_1}\\\\&=\frac{9}{4}\end{align*} Hence, the force becomes 2.25 times the original force. \[F_2=\frac 94 F_1\]
Problem (24): A stone is attached to the end of a rope of length $L$ and rotates in a vertical circle. At the top of the path, the tension in the rope is twice the weight of the stone.
(a) Determine the net force on the stone when it reaches the highest point of the path.
(b) What is the speed of the stone at this point?
After a few circles, when the stone is at the top of the circle, the rope is broken.
(c) Determine the time it takes the stone to hit the ground.
(d) Find the horizontal distance traveled by the stone before striking the ground.
Solution: This is left up to you to solve.
Summary:
In this article, we learned how to solve problems involving circular motion. The most important notes we practiced were as follows:
- An object moving in a circular path of radius $r$ at constant (uniform) speed $v$ experiences an acceleration whose magnitude is $a_c=\frac{v^2}{r}=r\omega^2$ and its direction is toward the center of the circle.
- Uniform circular motion is an example that shows that acceleration and velocity are not always in the same direction.
- In such motions, $\vec{a}$ and $\vec{v}$ are perpendicular.
Author: Dr. Ali Nemati
Date Published: 7-31-2021
