Magnetic force on a current carrying wire: Tutorial and Examples

Magnetic force on current-carrying wire problems with full explanations are provided for high school physics.

Introduction

Experiments show that when a wire carrying a current is immersed in a uniform magnetic field, a deflecting force is applied to it. But what is the physical origin of this force?

Recall that, once a moving charge encounters a magnetic field, a side-way force exerts on it. A wire-carrying current is made up of a very large number of such moving charges.

Let's go and see what happens inside a wire. Current in a wire is due to the movement of the conduction electrons (by convention, their movement is in the opposite direction of the current).

Suppose these electrons move toward the right with a drift velocity $v_d$. From the magnetic field, a force $\vec{F}_B$ of magnitude $ev_d B$ exerted on each such conduction electron.

The right-hand rule tells us that the direction of the force must be upward. Thus, we can conclude an upward force is applied to the wire due to an upward force exerted on each conduction electron inside it.

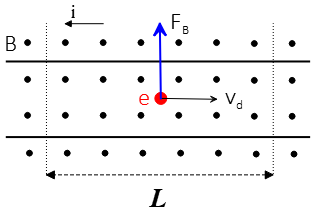
magnetic force on electrons inside wire

The above consequence is in full agreement with the experiment mentioned earlier.

Now, with this physics in mind, we want to derive the equation of force on a current-carrying wire in a magnetic field as below.

Consider a length $L$ of the wire immersed in a magnetic field directed out of the plane of the page and conduction electrons travel to the right. Those electrons with drift velocity $v_d$ take time $t=\frac{L}{v_d}$ to traverse the length $L$.

Thus, in that time a net charge of $q=it=\frac{iL}{v_d}$ passes through the end of the length. The magnetic force on this moving charge is \begin{align*} F_B&=q v_d B \sin \theta \\ \\ &=\Big(\frac{iL}{v_d}\Big)v_d B \sin 90^\circ\\ \\ &= iLB\end{align*} in above, $\theta = 90^\circ$ substituted since electrons move at a right angle with the magnetic field.

Therefore, the force on a straight wire carrying current $i$ and immersed in a uniform magnetic field $B$ that is perpendicular to the wire is determined as $F_B=i L B$.

We can generalize the above formula, to include the case in which the magnetic field is not perpendicular to the wire as \[ \vec{F}_B = i\vec{L}\times \vec{B} \] In this cross product, $\vec{L}$ is the length vector with a magnitude of length of that segment of the wire inserted into the magnetic field. The direction of this vector is directed along the direction of the current.

The magnitude of the force is also given as $F_B= i LB \sin \theta$, where $\theta$ is the angle between $\vec{L}$ and $\vec{B}$.

The direction of the $\vec{F}_B$ is perpendicular to the plane of $\vec{L}$ and $\vec{B}$ and is determined using the right-hand rule. Put your right four fingers along the current direction, so that your palm is directed toward the magnetic field direction, and your thumb shows the direction of the magnetic force.

In the following, some problems are presented for a better understanding of this topic

Magnetic force on a current-carrying wire problems

Problem (1): A current $i$ passes through a wire and is immersed in a uniform magnetic field B so that a maximum force applies to it, as shown in the figure below. Find the direction of the magnetic field.

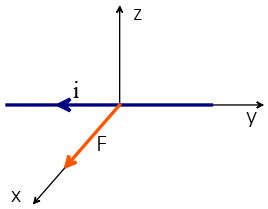
Solution: Method (I) using the right-hand rule
Put your right four fingers in the direction of the current $i$ so that the thumb points to the magnetic force. In this setup, your palm which is directed to the negative of the $z$-axis shows the direction of the magnetic field.

Method (II) using cross-product algebra
The equation of the magnetic force on a current-carrying wire is $\vec{F}_B=i \vec{L}\times \vec{B}$. In this example, the length vector $\vec{L}$ is toward the negative of y-axis that is $\vec{L}=L\,(-\hat{j})$ and force is to the x-axis , $\vec{F}_B=F_B\,(\hat{i})$. Substituting these vectors in the above formula, we have \begin{align*} \vec{F}_B &= i\vec{L}\times \vec{B} \\ F_B\,(\hat{i}) &= L\,(-\hat{j}) \times \vec{B}\end{align*} Thus, $\vec{B}$ must be directed to $-\hat{k}$ or $\hat{k}$ (since maximum force is obtained when force is perpendicular to both $L$ and $B$). From the cross-product algebra, one can deduce $B$ must be to $-\hat{k}$ to produce a vector along the $x$-axis.

Problem (2): A wire is extended horizontally and a constant current passes through it toward the east. The Earth's magnetic field is from south to north. What is the direction of the force applied to it from the earth's magnetic field?

Solution: first realize that, in a plane, directions are as follows: east is to the right, west to the left, north into the page, south out of the page, and up and down is trivial (see figure below).

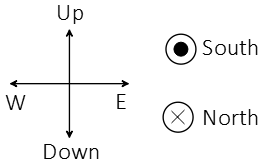
direction of a current-carrying wire problem in an external magnetic field

Thus, using the right-hand rule, the force on the wire is in the up direction.

Wire in a magnetic field

Problem (3): In the figure below, there is a magnetic field of magnitude 500 Gauss that extends horizontally from west to east. A straight wire of length L = 80 cm carrying current i = 25 A in the direction shown and placed at an angle of θ = 37° with horizontal into that magnetic field. What is the magnitude and direction of the magnetic force on this portion of the wire?

Solution: put the given data into the equation of force on a current carrying wire $F_B= i L B \sin \theta$ as follows \begin{align*} F_B &= i L B \sin \theta \\ &= 25\times 0.8 \times (500\times 10^{-4}) \times \sin 37^\circ \\ &= 0.6\quad {\rm N}\end{align*} Note that the $SI$ unit of the magnetic field is Tesla and recall that ${\rm 1\, G= 10^{-4}\, T}$.

Use the right-hand rule to find the direction of the magnetic force on a positive charge moving in a uniform $B$. Put your right fingers in the direction of the current and through the smaller angle curl them toward the magnetic field. The thumb points to the force direction. In this case, the force is into the page as $\otimes$.

Problem (4): A long and straight wire carrying the current i = 5 A is immersed in the magnetic field $\vec{B}=0.18\,\hat{i}+0.24\,\hat{j} \quad {\rm T}$. Find the maximum magnetic force on each meter of this wire.

Solution: Remember from the magnetic field problems section that the magnitude of the force exerted on a wire by a magnetic field is maximum when the direction of the wire is perpendicular to the field. Thus, the magnitude of the maximum force $F_{max} = i \ell B $ obtained as \begin{align*}F_{max} &= i \ell B \\ &=5\times 1\times 0.3 \\&= 1.5\quad {\rm N}\end{align*} where in above the magnitude of magnetic field vector is determined as below \begin{align*} B&=\sqrt{B_x^2+B_y^2}\\&=\sqrt{(0.18)^2+(0.24)^2}\\&=0.3\quad {\rm T}\end{align*}

Example (5): A straight wire of length $\ell=5\pi$ is formed into a semi-circle as shown in the figure below and placed in an external magnetic field of $B = 25\,{\rm G}$. If a current of $i=2\,{\rm A}$ passes through it, find the magnetic force on the wire due to the external magnetic field.

Solution: Recall that in the equation of magnetic force on a wire carrying current, $\vec{F}_B=i\vec{L} \times \vec{B}$, $\vec{L}$ was the length vector (or displacement vector) which extends from the initial point to the final point on the wire.

Here, the length vector $\vec{L}$ extends from left to right in the direction of the x-axis i.e. $\vec{L}=L\,\hat{i}$ where $L$ is equal to the diameter of the semi-circle and its magnitude is calculated as \begin{align*} \text{length of wire} &= \text{circumference of semi-circle} \\ 5\pi &= \pi \, r\\ \Rightarrow r&= 5\,{\rm cm} \end{align*} Thus, the diameter is $L=2r=10\,{\rm cm}$.

Now, we can find the magnitude of the force as \begin{align*} F &= i L B \sin \theta \\ &=2\times (5\times 10^{-2})\times (25\times 10^{-4})\times \sin 90^\circ \\ &= 5\times 10^{-3}\quad {\rm N}\end{align*}

Problem (6): In the figure shown, find the direction of the magnetic force 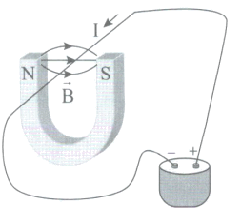on the segment of the wire inside the magnetic field.

Solution: the current flows out of the plane of the page, i.e. $\odot$, and the magnetic field is also directed from the west(left) to the east(right). Therefore, the force is exerted upward.

Right hand rule for direction of magnetic force on a wire

Problem (7): In the figure below, a piece of ABCDE wire is immersed into a uniform magnetic field B. What current must pass through the wire to exert a net force of 2 N from the magnetic field on the wire?

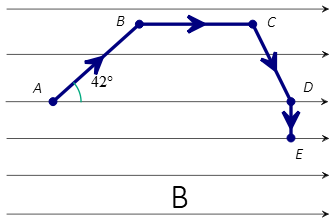
Solution: there are two methods to solve such problems. When a straight wire is formed into an arbitrary shape and inserted into a magnetic field, the easiest way to find the force on it is to draw the length vector $\vec{L}$ and then find the force on this vector.

Here, the length vector is plotted directly from A to E. This vector has two components, one is DE and the other is AD. The former is perpendicular to $B$ and the latter is parallel so its contribution to magnetic force is zero.

Thus, the DE part only contributes to the magnetic force since the angle between it and $B$ is $90^\circ$. Putting all these data into the equation $F_B=i\ell B \sin \theta$, we get the force on the whole ABCDE wire as below \begin{align*} F_B &=i\ell B \sin \theta \\ 2 &= i\,(0.1)\times 4\times \sin 90^\circ \\ \Rightarrow i&= 5\quad {\rm A}\end{align*}

Problem (8): in a part of space there is a uniform magnetic field $\vec{B}=12\,\hat{i}+5\,\hat{j}$. A long and straight wire carrying current $i=3\,{\rm A}$ is placed into that area at the right angle with the field. What is the net magnetic force on each meter of the wire?

Solution: first find the magnitude of the magnetic field as below \begin{align*} B&=\sqrt{B_x^2+B_y^2}\\&=\sqrt{12^2+5^2}\\ &=13 \quad {\rm T}\end{align*} next calculate the force on the wire using the equation of maximum magnetic force on a straight wire carrying current $i$ as \begin{align*} F_{max} &=i\ell B\\ &=3\times 13\times 1\\&=39\quad {\rm N}\end{align*} since the wire is perpendicular to the magnetic field so the force on it is maximum.

Summary:

The magnitude of the force on a wire carrying current i in an arbitrary magnetic field B is F = i L B sin θ, where θ is the smaller angle between the magnetic field and current.
The direction of the force is determined by the right-hand rule: put your right fingers along the direction of the current such that your palm points to the magnetic field and your thumb shows the force's direction.
The maximum magnetic force occurs when the angle between B and i be θ = 90°.
The force on an arbitrary part of a bent wire is the same as the force on a straight wire carrying the same current and extends between the two endpoints of that section.

Author: Dr. Ali Nemati

Date Created: 1/18/2021