Beat Frequency Problems: High School & College Physics
We are going to learn and practice some problems about beat frequency in high school physics. In each problem, you can also find a full explanation of this topic.
When two waves of nearly equal (or slightly different) frequencies interfere with each other, a new wave is produced whose amplitude (or intensity) oscillates with the frequency of $f_{beat}=|f_2-f_1|$, which is called the beat frequency.
In the following, we will solve several questions on beat frequency appearing in different situations.
Beat Frequency Problems
Problem (1): Two guitar strings are plucked, and sounds from them reach your ears at the same time. The frequency of the first string is $245\,\rm Hz$ and the second string has a frequency of $247\,\rm Hz$. What is the beat frequency?
Solution: Beats occur as a result of the superposition of two sound waves with slightly different frequencies of $f_1$ and $f_2$. In this case, the beat frequency is calculated by the following formula \[f_{beat}=|f_2-f_1|\] where $|\cdots|$ emphasizes that the absolute value of frequencies difference matters.
Here, the frequencies produced by guitar strings are $f_1=245\,\rm Hz$ and $f_2=247\,\rm Hz$. As you can see, these two frequencies are close to each other, so their difference gets the beat frequency \[f_{beat}=|247-245|=2\,\rm Hz\]
Problem (2): Consider two wave sources that produce waves of frequencies $15\,\rm Hz$ and $17\,\rm Hz$. What is the beat frequency between these two sources and explain some about its physical meaning?
Solution: The difference in frequency of two waves that differ slightly from each other produces a detectable tone that can be heard by a nearby listener. The volume or loudness of this tone varies with frequency $|f_1-f_2|$, which is called beat frequency.
In this case, the number of rises and falls in the detectable loudness pattern is \[f_{beat}=|15-17|=2\,\rm Hz\] This means that a nearby listener detects a sound that goes up and down in volume two times every second.
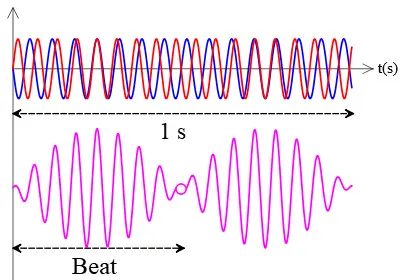
The following figure depicts a pattern of beats for this problem. Two waves of $17\,\rm Hz$ (red graph) and $15\,\rm Hz$ (blue graph) interfere and produce a pattern that goes through two maxima and two minima in one second (pink graph). This equals a beat frequency of two hertz because there are two beats every one second. This is a typical graph that appears in every beat frequency question.
Problem (3): Assume we sound two tuning forks at $440\,\rm Hz$ and $445\,\rm Hz$ simultaneously. What is the beat frequency heard by a nearby listener?
Solution: The number of beats per second heard when two tuners sound with slightly different frequencies is called the beat frequency. In this question, the two tuners have frequencies close together. Their difference gives the number of ''hums'' or beats heard in one second or the frequency of beats. \begin{align*} f_{beat}&=|f_2-f_1| \\ &=|440-445| \\&=5\,\rm Hz \end{align*}
Problem (4): Two tuning forks are struck at the same time, and a beat frequency of $5\,\rm Hz$ is heard. If one of the tuning forks has a frequency of $255\,\rm Hz$, find the frequency of the other tuning fork.
Solution: Here, we are given the beat frequency $f_{beat}=5\,\rm Hz$ and one of the two involving frequencies $f_1=255\,\rm Hz$. Applying the beat frequency formula $f_{beat}=|f_2-f_1|$, substituting the given numerical values into it and solving for the frequency $f_2$ gives \begin{align*} f_{beat}&=|f_2-f_1| \\ 5&=|f_2-255| \end{align*} In all beat frequency problems, we constantly encounter such expressions involving an equation with a absolute value.
To get through this step, it is important to note that the role of an absolute value is to produce a positive output. Keep in mind that frequency can not be a negative value in physics. With these explanations, we can infer that the second tuning fork $f_2$ can accept the following frequencies \[ \boxed{\rm 300\, Hz \, , \, 250\, Hz}\] Thus, these two frequencies of the second tuning fork exactly can interfere with the sound waves of the first tuning fork and produces a beat frequency of $5\,\rm Hz$.
Problem (5): Two nearby guitars are sounded together at frequencies of $525\,\rm Hz$ and $528\,\rm Hz$. When that occurs, what is the frequency of the resultant sound wave, and what is the beat frequency heard by a listener?
Solution: When two waves of different frequencies but equal amplitudes are combined (or interfere) with each other, the resultant wave has an effective frequency equal to the average frequency of $(f_1+f_2)/2$. In this case, a beat frequency of $f_{beat}=|f_1-f_2|$ is also heard by a listener close to them. These results are obtained using the superposition principle.
Thus, the resultant sound wave has a frequency of \[f=\frac{525+527}{2}=526\,\rm Hz\] and a beat frequency of \[f_{beat}=|525-528|=3\,\rm Hz\] The meaning of this expression is that the listener would hear a sound of $526\,\rm Hz$ that its loudness changes three times every second. This is the physical meaning of the beats.
Problem (6): We use a standard tuning fork that steadily vibrates at $196\,\rm Hz$ to tune the $G$ string on a violin. When it is struck and held near the violin string, $10$ beats per five seconds are counted. What are the possible frequencies produced by the violin string?
Solution: In this problem, the beat frequency has not been directly given in $\rm Hz$, but rather in terms of the frequency definition. In physics, the frequency is defined as the number of vibrations $\rm N$ divided by the total time interval $\rm t$ in which the vibrations occur. This can be expressed as: \[f=\frac{N}{t}\] Given that there are 10 beats per five seconds, we can calculate the frequency as: \[f=\frac{10}{5}=2\,\rm Hz\] This is the beat frequency heard by the tuner. In this case, the standard tuning fork vibrates at a frequency of $f_1=196\,\rm Hz$. Using the beat frequency formula and solving for the other unknown frequency gives us: \begin{align*} f_{beat}&=|f_2-f_1| \\ 2&=|f_2-196| \end{align*} This equation has two solutions: \[\boxed{\rm 198\,Hz \, , \, 194\,Hz}\] Either of these frequencies, when subtracted from the frequency of the tuning fork (196 Hz), will result in a beat frequency of 2 Hz.
Problem (7): A person holds a tuning fork vibrating at $255\,\rm Hz$ and moves toward a wall at a constant speed of $2\,\rm m/s$. How many beats per second does he hear between the tuning fork and its echo? How fast must he move away from the wall to recognize five beats per second?
Solution:
Problem (8): The $D$ string on a violin has a fundamental frequency of $294\,\rm Hz$. Consider its length and mass to be $32.5\,\rm cm$ and $0.383\,\rm g$. Another violinist wants to tune the $G$ string on her violin with this standard violin. When we sound that and hold near this identical out-of-tune violin, a beat frequency of $3\,\rm Hz$ is heard between the two strings. What is the length of the $G$ string on the other violin?
Solution: The two $G$ strings on both violins are identical, so both are made of the same material and
A violin is tuned by twisting (tightening or loosening) the tuning pegs. In this way, the effective lengths of $G, D, A, E$ strings become shorter or longer.
In this question, our standard or tuned $D$ string violin has a frequency of $294\,\rm Hz$.
Problem (9): Two organ pipes one has a length of $1.06\,\rm m$ and the other is $1.08\,\rm m$ long are open at one end but closed at the other. Assume both pipes are playing together in their fundamental frequencies. What is the frequency of the beats? (Take the speed of sound in the pipes to be $v=344\,\rm m/s$).
Solution: In a tube of length $L$, open at one end and closed at the other, the natural (or normal mode) frequencies of vibrations are odd multiples of wave speed in the medium $v$ divided by $4L$. \[f_n=n\frac{v}{4L}\, , \, n=1,3,5,\cdot\] The fundamental frequency is obtained by setting $n=1$. In this case, we have two organ pipes with lengths of $L=1.06\,\rm m$ and $L'=1.08\,\rm m$. The fundamental frequency ($n=1$) of each pipe are found as follows \begin{gather*} f_1=\frac{344}{4\times 1.06}=81.13\,\rm Hz \\\\ f'_1=\frac{344}{4\times 1.08}=79.63\,\rm Hz\end{gather*} As you can see, these two instruments produce two fundamental frequencies close in together. By definition, the beat frequency is known to be as follows \[f_{beat}=|81.13-79.63|=\boxed{1.5\,\rm Hz}\] For a nearby listener, these two sound waves that come from each pipe combine and create a wave of $\frac{81.13+79.63}{2}=80.38\,\rm Hz$ that its loudness varies in time as about $1.5$ times every second or $1.5\,\rm Hz$.
Problem (10): One tuning fork vibrates at $450\,\rm Hz$ while the other tuning fork simultaneously vibrates at an unknown frequency. A nearby listener identifies a tone that rises and falls in intensity four times per second. What is the frequency of the second tuning fork?
Solution: When two tuning forks or other musical instruments sound at slightly different frequencies at the same time, a tone whose intensity (or volume) rises and falls is heard. By counting these patterns, we can find the beat frequency between these two sound sources.
In this problem, the sound volume heard by a listener goes up and down four times every second. This is the same beat frequency that is written as $f_{beat}=4\,\rm Hz$ in hertz. Using the beat frequency formula and substituting the given numerical values into it gives \begin{align*} f_{beat}&=|f_1-f_2| \\\\ 4&=|450-f_2| \end{align*} Like all beat frequency problems, expressions like the above have two solutions, \begin{gather*} 450-f_2=4 \\ \Rightarrow \quad \boxed{f_2=446\,\rm Hz} \\\\ 450-f_2=-4 \\ \Rightarrow \quad \boxed{f_2=454\,\rm Hz} \end{gather*} Thus, the second tuning fork vibrates at either $446\,\rm Hz$ or $454\,\rm Hz$.
Problem (11): A guitar string creates $6$ beats per second when struck simultaneously with a $252-\rm Hz$ standard tuning fork and $4$ beats per second when sounded with a $250-\rm Hz$ tuning fork. What is the frequency of this string?
Solution: This question is a bit challenging. On the first try, six beats are heard with a $252-\rm Hz$ tuning fork. Thus, according to the beats formula we have \begin{gather*} f_{beat}=|f_1-f_2| \\ 6=|f_1-252| \end{gather*} Similarly, in the second try, $4$ beats per second is heard with $250-\rm Hz$ tuning fork, so \begin{gather*} f'_{beat}=|f_1-f'_2| \\ 4=|f_1-250| \end{gather*} where the frequency produced by the string is denoted by $f_1$. Both of the above expressions are of the type of absolute value equations, i.e. $|x-a|=b$. The standard solution to this type of equations is found as \[x-a=b\quad , \quad x-a=-b\] According to this formula, the beat frequency of the first try is obtained as below \begin{gather*} |f_1-252|=6 \\ f_1-252=6 \rightarrow f_1=258\,\rm Hz \\ f_1-252=-6 \rightarrow f_1=246\,\rm Hz \end{gather*} In a similar manner, the second try gives the following frequencies for the guitar string \begin{gather*} |f_1-250|=4 \\ f_1-250=4 \rightarrow f_1=254\,\rm Hz \\ f_1-250=-4 \rightarrow f_1=246\,\rm Hz \end{gather*} As you can see, the $246\,\rm Hz$ frequency is the common solution of these two equations derived from the above experiments. Thus, the frequency of the guitar string is known to be $\boxed{246\,\rm Hz}$.
Problem (12): Two strings, fixed at both ends, are struck together. When that occurs, a nearby listener hears three beats every $1.5$ seconds. The string one is assumed to be vibrating at a $196\,\rm Hz$. (a) What is the frequency of the other string? (b) If we want to bring them in tune, by how much must the tension in the second string be increased or decreased?
Solution: These two strings could be strings of two different identical
Three beats every $1.5$ second, by the definition of frequency as the number of complete cycles divided by the time taken, can be translated as $f_{beat}=\frac{3}{1.5}=2\,\rm Hz$ in hertz.
(a) The first both ends string is sounded at $196\,\rm Hz$. The frequency of the second string is computed as follows \begin{gather*} f_{beat}=|f_1-f_2| \\ 2=|196-f_2| \\ \Rightarrow 196-f_2=2 \rightarrow \boxed{f_2=194\,\rm Hz} \\\\ \rm and\, 196-f_2=-2 \rightarrow \boxed{f_2=198\,\rm Hz} \end{gather*} Either frequencies are allowed.
(b) Being in tune means that there are no longer beats between these two strings. The frequency of vibrations of a vibrating stretched string of length $L$, fixed at both ends, is related to the tension $F$ in the string by the following formula \[f_n=\frac{n}{2L}\sqrt{\frac{F}{\mu}}\] where $\mu=\frac{m}{L}$ is the string's linear mass density and $n=1,2,3,\cdots$ determines the mode of vibrations. Hence, the frequency of oscillations on the string is directly proportional to the square root of tension in the string, i.e., $f\propto\sqrt{F}$ or $F\propto f^2$. Originally, one of the possible frequencies is $f'=194\,\rm Hz$. To bring this to the other string frequency, $f=196\,\rm Hz$, we need to adjust the tension in that string as below \begin{gather*} \frac{F'}{F}=\left(\frac{f'}{f}\right)^2 \\\\ \frac{F'}{F}=\left(\frac{194}{196}\right)^2 \\\\ \rightarrow F'=0.980F \end{gather*} This relation tells us that if we want to eliminate the beats between these two fixed strings, the tension in the string with unknown frequency should be $0.980$ the tension in the string with known frequency. The difference between these two tensions gives the amount of reduction in the tension \[\Delta F=F'-F=-0.020F\] where the negative indicates a reduction in the tension. Thus, the tension in the other string must decrease by $2.0\%$.
Similarly, the change in the string's tension for the other possible frequency, $198\,\rm Hz$, is also obtained as an increase by $2.0\%$.
Problem (13): Two guitar strings are tuned to play the same frequency $324\,\rm Hz$. By twisting the tuning peg of that string on one of them, its tension is decreased by $1.5\%$. By doing that, what will be the beat frequency heard when the two strings are played together?
Solution: The strings on a guitar are fixed at both ends. In the section related to the standing wave problems, we learned that by playing these strings with both ends fixed, standing waves would form on the string whose frequencies are found using the following formula \[f_n=n\frac{v}{2L},\, n=1,2,3,\cdots \] where $n$ denote the modes of the standing waves and $v$ is the speed of waves on the string. On the other hand, the speed of a wave traveling on a stretched string of mass per unit length $\mu=\frac{m}{L}$ and under tension $F$ is given by \[v=\sqrt{\frac{F}{\mu}}\] By combining the two equations above, the frequency produced on a stretched string is related to the tension by \[f=\frac{n}{2L} \sqrt{\frac{F}{\mu}}\] Thus, the frequency is directly proportional to the square root of tension in the string, i.e., $f\propto \sqrt{F}$.
Initially, the two strings are under the same tension, i.e., $F_2=F_1$ but later the tension in one of them, say the second string, is decreased by $2.5\%$. This means that the tension in that string is \[F_{new}=F_1-0.015F_1=1.0985F_1\] The frequency produced by this string is also changed as follows \begin{gather*} \frac{f_{new}}{f_{old}}=\sqrt{\frac{F_{new}}{F_{old}}} \\\\ \frac{f_{new}}{324}=\sqrt{\frac{0.0985F_1}{F_1}} \\\\ \quad f_{new}=324\sqrt{0.0985} \\\\ \Rightarrow \boxed{f_{new}=321.56\,\rm Hz} \end{gather*} The other guitar string plays the same $324\,\rm Hz$. The difference between these two frequencies gives the beat frequency heard by a guitar tuner. \[f_{beat}=|321.56-324|=\boxed{2.44\,\rm Hz}\] That means a tuner can realize every one second $2.44$ times change in the volume or loudness of the sound between the two guitar strings.
Author: Ali Nemati, Ph.D.
Published: 4/3/2022
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
