Standing Waves Problems with Answers for AP Physics
A standing wave, in physics, is a wave that is the result of the interference of two waves of equal frequency travel in opposite directions.
The formula of a standing wave is written as below \[f_n=n\frac{v}{2L}\] or \[f_n=nf_1\] where $L$ is the length of the string, $v$ is the speed of the wave on the string, and $m$ is a positive integer.
In this tutorial, we want to learn about standing waves by solving plenty of practice problems.
Standing Wave: Formation
Suppose you move up and down one end of a string that is fixed at the other end. The pulse created in this way on the string, will travel down to the fixed end and be reflected back as an inverted same pulse.
Now suppose, shaking the string at a steady rate, you create continuous waves of such pulses on the string.
In this case, some pulses travel down the string, and some other reflected pulses come back.
These trains of incoming and outgoing waves can interfere with one another and produce a brand new wave, called a standing wave.
It is called "standing wave'' because it does not appear to be traveling in time. It only oscillates up and down in a fixed pattern.
When the traveling (incident) and reflected waves (outgoing) combine in accord with the superposition principle, some points along the string are the place of constructive and destructive interference.
Destructive interference occurs when two traveling waves with the same magnitude of displacement but opposite signs, combine with each other. Consequently, at these points, the amplitude of the resultant wave becomes zero.
Such points with a net-zero displacement are called nodes.
Similarly, when two traveling waves have both the same magnitude of displacement and sign combine with each other, the total displacement at that point becomes the maximum value.
Such points with a maximum displacement (amplitude) are called antinodes.
At nodes, there is no motion in the string. Midway between two adjacent nodes, there is always an antinode.
Consequently, the characteristic of standing waves is this alternating pattern of nodes and antinodes. Whenever this pattern is formed on a stretched string, we say a standing wave has been produced.
Vibrations that are produced on a stretched string, which are called standing waves, are similar to the same vibrations observed in the simple harmonic motion, or simple pendulum.
The main difference between them is that the vibrations on a string can have an infinite number of allowed frequencies but for the latter cases there is only one natural frequency.
Standing Wave: Solved Problems
Problem (1): The standing wave pattern is observed in a stretched string fixed at both ends, as shown in the figure below. If the speed of the waves in the string is $2\,{\rm m/s}$, at what frequency is this standing wave vibrating?
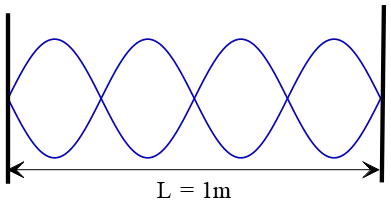
Solution: In the standing wave pattern shown, there are four loops or antinodes. These loops fit into the length of the string $L$. On the other side, recall that each loop has a length of $\ell=\frac{\lambda}{2}$. So, the whole length of this string can accommodate four of these loops i.e. $L=4\ell$ or $L=4(\lambda/2)$.
The wave speed and wavelength are also related together by $\lambda=\frac{v}{f}$. Substituting this into the length formula above, we get \[L=4(\frac{\lambda}{2})=2\lambda=2\frac{v}{f}\] Rearranging this relation and putting the numerical values, the required frequency is obtained as \[f=2\frac{v}{L}=2\left(\frac{2}{1}\right)=4\quad {\rm Hz}\] We also could find this frequency from the standing wave formula directly. According to this formula, the number of loops or antinodes $n$ produced in the taut string is directly proportional to the frequency of vibrations and are related together by the following equation \[f_n=n\,\frac{v}{2L}\] By substituting the given numerical into the above equation, we get the same previous result.
Problem (2): An string is tightly fixed at both ends and is driven by a $60-{\rm Hz}$ oscillator so that a standing wave pattern is observed as shown. Suppose the tension in the cord and its mass per unit length do not change. In this case, which of the following frequencies will not be produced along this cord?
(a) 40 Hz (b) 100 Hz (c) 30 Hz (d) 200 Hz
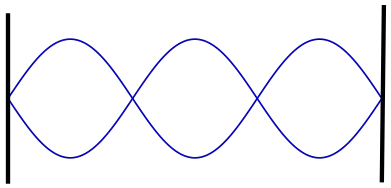
Solution: To find the allowed frequency of vibrations along a stretched string of length $L$ with a wave speed of $v$, we must find the fundamental frequency. Because the other allowed frequencies are (positive) integral multiples of this frequency and are also related to it by $f_n=nf_1$ where $n$ is the number of loops formed across the string.
The fundamental frequency is a vibration that has one loop or one antinode. Thus, if we set $n=1$ in the standing wave formula, $f_n=n\,\frac{v}{2L}$, we get the fundamental frequency. \[f_1=\frac{v}{2L}\] But in this example, neither $v$ nor $L$ is given. We can find them or their ratio from the given frequency of the pattern formed on the string as shown in the figure.
In this pattern, we observe three loops so setting $n=3$ and $f_3=60\,{\rm Hz}$ in the standing wave equation, we get \begin{align*} f_3&=3\frac{v}{2L}\\\\ 60&=3\frac{v}{2L} \\\\ \Rightarrow \frac{v}{2L}&=20 \end{align*} Next, substitute this ratio into the fundamental frequency equation to find it as \[f_1=\frac{v}{2L}=20\quad{\rm Hz}\] Now that we have this frequency, the other allowed oscillation are positive integer multiple of this vibration \begin{gather*} f_n=nf_1\\f_2=2\times 20=40\quad {\rm Hz}\\f_3=3\times 20=60\quad {\rm Hz}\\f_4=4\times 20=80\quad {\rm Hz}\\f_5=5\times 20=100\quad {\rm Hz}\end{gather*} Consequently, frequency 30 Hz will not form along this string because it is not a whole-number multiple of the fundamental frequency 20 Hz.
Problem (3): Which of the following frequencies are higher harmonics of a taut string fixed at both ends with a fundamental frequency of 250 Hz?
(a) 150 Hz (b) 500 Hz (c) 700 Hz (d) 1000 Hz
Solution: The vibrations produced in a stretched string fixed at both ends have frequencies as $f_n=nf_1$, where $f_1$ is the fundamental frequency, and $n$ is an integer indicates the higher harmonics.
So, the higher frequencies are the positive integer multiples of the fundamental (first) harmonic. The integer multiple of $f_1=250\,{\rm Hz}$ are as below \begin{gather*} 1 \times 250=250\,{\rm Hz}\\2 \times 250=500\,{\rm Hz}\\3 \times 250=750\,{\rm Hz}\\4 \times 250=1000\,{\rm Hz}\end{gather*} As you can, the frequency $500\,{\rm Hz}$ is the second harmonic and $1000\,{\rm Hz}$ is the fourth harmonic.
Thus, the correct choices are (b) and (d).
Problem (4): The adjacent antinodes of a standing wave formed on a stretched string fixed at both ends are separated by $20\,{\rm cm}$. Waves travel along the string at a speed of $1200\,{\rm cm/s}$. At what frequency is the string plucked to produce such a standing wave?
Solution: Keep in mind that in all the standing wave problems, the distance between two adjacent nodes or antinodes is half of the wavelength. So, $d=\frac 12 \lambda$. Of this relation, we can find the wavelength of the corresponding standing wave. \[20=\frac{\lambda}{2} \Rightarrow \quad \lambda=40\,{\rm cm}\] Given the wavelength and wave speed, we can find the corresponding frequency using the following formula \[f=\frac{v}{\lambda}=\frac{1200}{40}=30\,{\rm Hz}\]
Problem (5): A stretched cord is vibrated in three loops at a frequency of 240 Hz. Find the other three frequencies at which it resonates.
Solution: According to the standing wave formula, $f_n=n\frac{v}{2L}$, the frequency of other vibrations produced on a taut string fixed at both ends is related to the fundamental frequency as $f_n=nf_1$.
In this formula, $n$ is a positive integer indicating the number of antinodes on the standing wave. Here, we have three loops. Recall that each loop corresponds to an antinode. So, this standing wave has three antinodes, $n=3$.
We are told $f_3=240\,{\rm Hz}$. Thus, the fundamental frequency gets as below \[f_1=\frac{f_n}{n}=\frac{240}{3}=80\,{\rm Hz}\] Having this first harmonic, we can find other harmonics or frequencies because the others are positive integer multiple of this fundamental frequency. \[f_n=80n\] Hence, the frequency of other vibrations on the string is computed as below \begin{gather*} f_2=2\times 80=160\,{\rm Hz}\\\\f_3=3\times 80=240\,{\rm Hz}\\\\f_4=4\times 80=320\,{\rm Hz}\\\\f_5=5\times 80=400\,{\rm Hz}\end{gather*} And so on. Now, we want to choose a name for each frequency of vibrations.
All frequencies of standing waves produced on the string are called harmonics.
The lowest frequency of a standing wave is called fundamental frequency or first harmonic and corresponds to one antinode.
The other frequencies or harmonics have another name, called overtones.
For example, the next mode of vibration after the first harmonics is called the second harmonic or first overtone. This mode has two loops or two antinodes.
With these explanations, the frequency of vibrations of this particular standing wave computed above, except the fundamental, are named as below \begin{gather*} f_2 \rightarrow \text{first overtone}\\\\f_3 \rightarrow \text{second overtone}\\\\f_4 \rightarrow \text{third overtone}\end{gather*}
Problem (6): The frequency of standing waves on a taut string is $435\,{\rm Hz}$. The waves travel on the string at a speed of $95\,{\rm m/s}$. How far apart are two adjacent nodes?
Solution: The frequency and speed of waves on a stretched string are given. We can relate those to wavelength using the standard formula $\lambda=\frac{v}{f}$. So, the wavelength of this particular standing wave produced on the string is \[\lambda=\frac{v}{f}=\frac{95}{453}=0.22\,{\rm m}\] Recall that the distance between two adjacent nodes or antinodes in a standing wave is half the wavelength, $d=\frac 12 \lambda$. Thus, a pair of adjacent nodes of this standing wave is separated by $11\,{\rm cm}$.
Problem (7): Two successive overtones of a vibrating guitar string are $280\,{\rm Hz}$ and $350\,{\rm Hz}$. Find the frequency of the first harmonic?
Solution: Overtone is a name for other frequencies except the fundamental frequency. Suppose $f_n=280\,{\rm Hz}$, where $n\neq 1$, to be an unknown overtone. The next overtone after this is obtained by increasing $n$ by one as $n\rightarrow n+1$. So, the other next overtone is $f_{n+1}=350\,{\rm Hz}$.
Standing wave formula relates the other overtones to the first harmonic or fundamental frequency as $f_n=nf_1$. Divide those two overtones by each other and solve for $n$. \begin{gather*} \frac{f_n}{f_{n+1}}=\frac{n}{n+1} \\\\ \frac{280}{350}=\frac{n}{n+1} \\\\\rightarrow 280(n+1)=350n\end{gather*} Solving the above equation, gets \begin{align*} 280(n+1)&=350n\\280n+280&=350n\\280&=350n-280n\\ 280&=70n\\\Rightarrow n&=280/70\\&=4\end{align*} This indicates that this particular standing wave formed on the string has four antinode or four loops.
Using the value of one of the given above overtone and substitute $n=4$ into it, we can find the fundamental frequency, $f_1$. \begin{gather*} f_n=nf_1\\ f_4=4f_1\\280=4f_1 \\\Rightarrow f_1=280/4=70\,{\rm Hz}\end{gather*} Hence, the frequency of the first harmonic is $70\,{\rm Hz}$.
Problem (8): The following figure shows a standing wave vibrating on a string at a frequency of $100\,{\rm Hz}$. At what speed do the waves travel on the string?
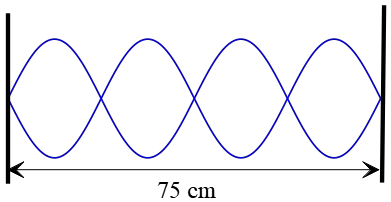
Solution: The length of the string is given $L=75\,{\rm cm}$. As you can see, there are four loops or four antinodes (denoted by $N$ in the figure) across this length, so $n=4$. Remember the distance between two adjacent nodes, as shown in the figure, is half the wavelength. In other words, each loop in a standing wave represents half a wavelength.
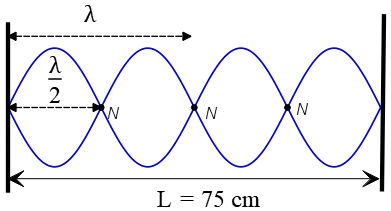
In this case, four loops make the whole length of the string. So, $4\frac{\lambda}{2}=L$. This relation gives us the wavelength as \[4\frac{\lambda}{2}=76 \Rightarrow \lambda=38\,{\rm cm}\] Now that the wavelength is found, we can use the formula $v=f\lambda$ to find the wave speed. \[v=f\lambda=100\times 0.38=38\,{\rm m/s}\] Note that we converted $cm$ to SI unit of length, $m$.
Problem (9): A standing wave is produced on a 2-m-long taut string fixed at both ends. The speed of the wave is $60\,{\rm m/s}$.
(a) At what frequency does the string vibrate?
(b) What is this harmonic called?
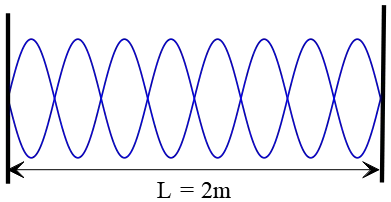
Solution: According to the standing wave formula, the frequency of vibrations on a stretched string fixed at both ends is given by \[f_n=n\frac{v}{2L}\] where $n$ is the number of loops or antinodes formed along the string.
(a) In this example, there are eight loops so $n=8$. So, the oscillation that is produced along this string, as shown in the figure, has a frequency of \begin{align*} f_n&=n\frac{v}{2L}\\\\ f_8&=8\,\frac{60}{2\times 2}\\\\&=120\quad {\rm Hz}\end{align*}
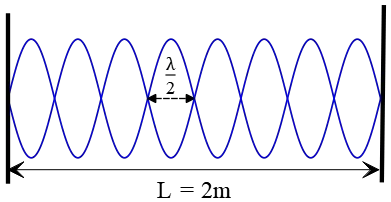
(b) This vibration is called the eighth harmonic or seventh overtone.
Problem (10): In an experiment is observed that a wave with five equal segments forms on a stretched string of length $L$ by a $630-{\rm Hz}$ oscillator. What oscillator frequency does make three equal loops in the string?
Solution: Equal segments or loops are characteristic properties of a standing wave on a stretched string. Five equal segments correspond to $n=5$ whose frequency of this particular vibration is given as $f_5=630\,{\rm Hz}$. Let the fundamental frequency of this string be $f_1$.
Other harmonics are related to the fundamental frequency using the standing wave formula, $f_n=n f_1$. We are asked to find the frequency at which the driven oscillator must be set up to form three equal segments on the same string i.e. $f_3=?$.
Dividing $f_3$ by $f_5$, the fundamental frequency cancels. Solving the remaining relation for $f_3$, we get the wanted frequency \begin{gather*} \frac{f_3}{f_5}=\frac{3\times f_1}{5\times f_1}\\\\ \frac{f_3}{630}=\frac 35 \\\\ \Rightarrow f_3=378\quad {\rm Hz}\end{gather*}
Problem (11): A $3-{\rm cm}$ stretched string fixed at both ends, vibrates in its third harmonic at a frequency of $60\,{\rm Hz}$. What is the speed of the traveling transverse waves on the string?
Solution: The known information is the length of the string $L=3\,{\rm cm}$, the frequency of third harmonic $f_3=60\,{\rm Hz}$. We are told that the string oscillates in its third harmonic, so there must be formed three equal loops on the string i.e. $n=3$.
Putting all these information in the standing wave formula, $f_n=n\frac{v}{2L}$, and solving for $v$, we get \begin{gather*}f_n=n\frac{v}{2L} \\\\ 60=3\,\frac{v}{2\times 0.03}\\\\ \Rightarrow \quad v=1.2\,{\rm m/s}\end{gather*} Hence, the transverse waves travel down and reflected back at a speed of $1.2\,{\rm m/s}$.
Problem (12): A person plucks a C note on a guitar string. As a result, it oscillates at a fundamental frequency of $261\,{\rm Hz}$. Let the speed of waves on the string be $400\,{\rm m/s}$. What is the length of the guitar string?
Solution: Fundamental frequency has one loop or one antinode so $n=1$. Applying standing wave formula, we have \begin{align*}f_n&=n\frac{v}{2L}\\\\261 &=(1)\,\frac{400}{2L} \\\\\Rightarrow L&=0.766\quad {\rm m}\end{align*} Thus, the guitar string is about 76.6 cm long.
Problem (13): A $60-{\rm cm}$ stretched string fixed at both ends is plucked and released so that the first overtone of $1050\,{\rm Hz}$ is produced on it. How fast do the transverse vibrations travel on the string?
Solution: "First overtone'' means the second harmonic, so $n=2$. Using standing wave formula, and solving for $v$, we get \begin{align*}f_n&=n\frac{v}{2L}\\\\1050 &=(2)\,\frac{v}{2\times 0.6} \\\\\Rightarrow v&=630\quad {\rm m/s}\end{align*}
Summary:
In this long article, we practiced a few problems about standing waves.
Standing wave equation relates the frequency of vibrations $f$ of a standing wave pattern formed on a stretched string to the number of loops $n$, the speed of waves $v$ on the string, and the length $L$ of the string as below \[f_n=\frac{nv}{2L}\] This equation tells us also that across the length of a taut string can form different natural frequencies, called harmonics, that are related to the first or fundamental harmonic by formula $f_n=nf_1$.
In all standing waves problems, the fundamental frequency is written by the formula \[f_1=\frac{v}{2L}\]
Author: Ali Nemati
Date Published: 9/8/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
