Capacitance Problems and Solutions for High School

Some problems about air-filled parallel-plate capacitance are presented and solved. These questions are for high school and college students. Each solution is designed so that it be a self-tutorial on this subject.

Capacitance Definition: Problems

Problem (1): How much charge is deposited on each plate of a $4-\rm \mu F$ capacitor when it is connected to a $12\,\rm V$ battery? Now, connect the same capacitor to a $1.5\,\rm V$ battery. How much charge is stored?

Solution: The ratio of the charge stored on the plates of a capacitor to the potential difference (voltage) across it is called the capacitance, $C$: \[C=\frac{Q}{V}\] This equation defines the capacitance of a capacitor. The SI unit of capacitance is the farad ($\rm F$), which is equivalent to coulombs per volt, or \[\rm 1\,F = 1\, \frac{C}{V}\] In the first case, the charge deposited on each plate is calculated as \begin{align*} Q&=CV \\ &=(4\times 10^{-6})(12) \\&=48\,\rm \mu C\end{align*} Similarly, for the second case, we find: \begin{align*} Q&=CV \\ &=(4\times 10^{-6})(1.5) \\&=6\,\rm \mu C\end{align*} Note that the italic letters $V$ and $C$ represent voltage and capacitance, respectively, while non-italic letters $\rm V$ and $\rm C$ denote the units volts and coulombs.

Problem (2): In each plate of a $4500-\rm pF$ capacitor is stored plus and minus charges of $25\times 10^{-8}\,\rm C$. What is the potential difference across the plates?

Solution: By definition, the capacitance is given by $C=\frac{Q}{V}$. Solving for ($V$) and substituting the numerical values, we get: \[V=\frac{Q}{C}=\frac{25\times 10^{-8}}{4500\times 10^{-12}}=55.5\,\rm V \] However, when you calculate this, it should give: \[V = \frac{25 \times 10^{-8}}{4500 \times 10^{-12}} = 5.555\ldots \] Which rounds to: \[ V = 5.56,\text{V} \] Note that picofarad $=10^{-12}\,\rm F$. And indeed, we only enter the magnitude of charge into the formula, not its sign. It’s important to keep track of units and significant figures in your calculations.

Problem (3): The potential difference between two conductors each having charges of $+6\,\rm \mu C$ and $-6\,\rm \mu C$ is $12\,\rm V$.
(a) Determine the capacitance of this system.
(b) If the charges on each are increased to $+120\,\rm \mu C$ and $-120\,\rm \mu C$, how does the potential difference between them change?

Solution: Two conductors with equal and opposite charges will have a potential difference developed between them.

The capacitance in physics is defined as the ratio of the charge placed on each conductor to the voltage across them.

(a) Plugging in the values, we have \[C=\frac{Q}{V}=\frac{6\times 10^{-6}}{12}=0.5\times 10^{-6}\,\rm F\] Thus, the capacitance of this configuration is $0.5\,\rm \mu F$.

(b) Again, we have \[V=\frac{Q}{C}=\frac{120\times 10^{-6}}{0.5\times 10^{-6}}=240\,\rm V\]

Air-filled Parallel-plate Capacitor: Problems

Problem (4): Each plate of a parallel-plate capacitor, which is $2.5\,\rm mm$ apart in vacuum, carries a charge of $45\,\rm nC$. As a result, a uniform electric field of strength $2.5\times 10^6\,\rm V/m$ is formed between them.
(a) What is the potential difference between the plates?
(b) What is capacitance?
(b) What is the area of each plate?

Solution: Given data: $d=2.5\times 10^{-3}\,\rm m$, and $Q=45\times 10^{-9}\,\rm C$.
(a) We learned in the section on electric potential difference problems that the magnitude of a uniform electric field between two points separated by distance $d$ is related to the potential difference (or voltage) between those points by the formula $V=Ed$.
Substituting the given values gives: \[V=(2.5\times 10^6)(2.5\times 10^{-3})=6.25\,\rm kV\] where $k$ denotes kilo = $10^3$.

(b) Using the definition of capacitance, $C=\frac{Q}{V}$, we have: \[C=\frac{45\times 10^{-9}}{6.25\times 10^3}=7.2\,\rm pF\] where $p$ denotes pico = $10^{-12}$.

(c) The capacitance of an air-filled capacitor is given by $C=\epsilon_0 \frac{A}{d}$. Substituting the numerical values into this equation and solving for $A$ gives: \begin{align*} A&=\frac{Cd}{\epsilon_0} \\\\ &=\frac{(7.2\times 10^{-12})(2.5\times 10^{-3})}{9\times 10^{-12}} \\\\ &=2\times 10^{-3}\,\rm m^2 \end{align*} Hence, each plate has an area of $20\,\rm cm^2$ or, if it’s a square, each side would be approximately $4.47\,\rm cm$ long.

Problem (5): In a parallel plate capacitor the plates have an area of $0.46\,\rm m^2$ and are separated by $2\,\rm mm$ in a vacuum. It is then connected to a $3\,\rm kV$-battery. Calculate:
(a) the capacitance of the capacitor.
(b) the charge stored on each plate.
(c) the electric field between the plates.
(d) the charge density on one of the plates.

Solution: In this capacitance problem, we are given a special type of capacitor known as a parallel plate capacitor. When two oppositely charged parallel plate conductors, each with an area $A$, are brought close together at a distance $d$, the capacitance of this system is given by: \[C=\epsilon \frac{A}{d}\] where $\epsilon$ is the permittivity of the medium between the plates. When the plates are in the vacuum, we have $\epsilon = \epsilon_0 = 8.85\times 10^{-12}\,\rm F/m$.

(a) With the space between the plates being a vacuum, the capacitance of this parallel-plate capacitor is calculated as follows: \begin{align*} C&=\epsilon_0 \frac{A}{d}\\\\ &=8.85\times 10^{-12}\frac{0.46}{2\times 10^{-3}} \\\\ &=2.035\times 10^{-9}\,\rm F\end{align*} Hence, the capacitance is approximately $2$ nanofarads, or $C=2.035\,\rm nF$.

(b) Given the capacitance and voltage across the plates, we use the definition of capacitance to find the charge: \[Q=CV=(2\times 10^{-9})(3\times 10^3)=6\times 10^{-6}\,\rm C\] Therefore, the charges of $+6\,\rm \mu C$ and $-6\,\rm \mu C$ are stored on each plate of the capacitor.

(c) Since each plate has an equal amount of charge with opposite signs, a uniform electric field is formed between them. Generally, the electric field between the plates of a parallel-plate capacitor is given by: \[E=\frac{V}{d}\] where $V$ is the potential difference between the plates. Substituting the given numerical values, we get: \[E=\frac{3\times 10^3}{2\times 10^{-3}}=1.5\times 10^6 \,\rm V/m \]

(d) The surface charge density ($\sigma$) on each plate of a capacitor is defined by: $\sigma=\frac{Q}{A}$ where $A$ is the area of the plate and $Q$ is the net (total) charge on each plate. Thus, \[\sigma=\frac{Q}{A}=\frac{6\times 10^{-6}}{0.46}=13\times 10^{-6}\,\rm C/m^2 \]

Problem (6): We want to make a parallel-plate capacitor of $0.5\,\rm pF$ with two plates of area $100\,\rm cm^2$ spaced in a vacuum. What spacing must the plates have to achieve this goal?

Solution: Substitute the known information into the parallel-plate capacitor formula $C=\epsilon_0 \frac{A}{d}$, and solve for the unknown distance separation $d$: \begin{align*} d&=\frac{\epsilon_0 A}{C} \\\\ &=\frac{(8.85\times 10^{-12})(100\times 10^{-4})}{0.5\times 10^{-12}} \\\\ &=17.7\times 10^{-2}\,\rm m \end{align*} Notice that the area of each plate was given in $\rm cm^2$ which must be converted in $\rm m^2$ as follows: \[\rm 1\,cm^2=10^{-4}\,m^2\] Placing two equally and oppositely charged plates of area $\rm 0.01\,m^2$ at a distance of $17.7\,\rm cm$ from each other makes a $0.5\,\rm pF$ capacitor.

Problem (7): A $24-\rm V$ voltage is applied across the circular plates of a parallel-plate capacitor of $10\,\rm \mu F$.
(a) How much charge is stored on one of the plates?
(b) If the radius of the plates is doubled, how much charge would be deposited on each plate without the capacitor being separated from the battery?

Solution: Here, the plates that make up a parallel-plate capacitor are circular with an area $A=\pi r^2$ where $r$ is the radius of the plates.

(a) Given the potential difference (or voltage) and the capacitance, we use the definition of capacitance $C=\frac{Q}{V}$ to find the charge stored on each plate: \[Q=CV=(10\times 10^{-6})(24)=240\,\rm \mu C\]
(b) It’s important to note that in all capacitance problems, while the capacitor is connected to the battery, any change to the capacitor (like a change in area or plate spacing) maintains the voltage across the plates constant. Thus, changing the radius of plates does not lead to a change in the voltage between the plates, but the capacitance does change.

According to the parallel-plate capacitance formula, $C=\epsilon \frac{A}{d}$, by keeping the plate spacing constant, the change in the capacitance is given by: \begin{align*} \frac{C}{C'}&=\frac{A}{A'}=\frac{\pi r^2}{\pi r'^2} \\\\ &=\left(\frac{r}{2r} \right)^2 \\\\ \Rightarrow C&=\frac 14 C' \end{align*} As a result, by doubling the radius of the plates, the capacitance becomes four times the original one.

The original capacitance of the capacitor is $C=10\,\rm \mu F$, so the final capacitance if the radius is doubled is: \[C'=\frac 14 C=2.5\,\rm \mu F\] Now, multiply the new capacitance by the voltage across the plates to find the new charge stored on the plates after the changes are made: \[Q'=C'V= (2.5\times 10^{-6})(24)=60\,\rm \mu C\] Whenever you make changes in the geometry of a capacitor while it is connected to a battery, its capacitance and the charge on its plates change accordingly.

Problem (8): The charges deposited on each plate of a square parallel-plate air capacitor of capacitance $250\,\rm pF$ are $0.140\,\rm \mu C$. The plates are $0.126\,\rm mm$ apart.
(a) What is the potential difference between the plates?
(b) What is the area of one plate?
(c) What is the magnitude of the electric field between the plate?
(d) What is the surface charge density on one plate?

Solution: In all capacitance problems, we have two principal equation: capacitance definition $C=\frac{Q}{V}$, and parallel-plate capacitance, $C=\epsilon \frac{A}{d}$.

(a) The capacitance and the charge stored on each plate are given. We solve for $V$ in the first equation and substitute the given values, \[V=\frac{Q}{C}=\frac{0.140\times 10^{-6}}{250\times 10^{-12}}=560\,\rm V\]
(b) In this case, between the plates is filled with a vacuum, so $\epsilon=\epsilon_0$. Using the equation $C=\epsilon_0 \frac{A}{d}$ and solving for $A$ gives \begin{align*} A&=\frac{Cd}{\epsilon_0} \\\\ &=\frac{(250\times 10^{-12})(0.126\times 10^{-3})}{9\times 10^{-12}} \\\\&=0.0035\,\rm m^2 \end{align*} This is equivalent to a square of side length $0.06\,\rm m$ or $6\,\rm cm$.

(c) The electric field between the plates of a parallel-plate capacitor is uniform, so we can use the equation $E=\frac{V}{d}$ \[E=\frac{560}{0.126\times 10^{-3}}=4.4\times 10^6\,\rm V/m \]
(d) The surface charge density is $\sigma=\frac{Q}{A}$ where $A$ is the plate area. In this case, the plates are a square of area $0.0035\,\rm m^2$ on which a charge of magnitude $0.140\,\rm \mu C$ is stored. Therefore, \[\sigma=\frac{0.140\times 10^{-6}}{0.0035}=4\times 10^{-5}\,\rm C/m^2 \]

Problem (9): How strong is the electric field between the regions of an air-filled $5-\rm \mu F$ parallel capacitor that its plates are $2\,\rm mm$ apart and holds a charge of $56\,\rm \mu C$ on each plate?

Solution: The electric field between the plates of a parallel-plate capacitor is determined by $E=\frac{V}{d}$ where $V$ is the potential difference between the plates and is related to the charge on each plate by $C=\frac{Q}{V}$. Solving this equation for $V$ and plug in the given values of $C$ and $Q$, gives \[V=\frac{Q}{C}=\frac{60\times 10^{-6}}{5\times 10^{-6}}=12\,\rm V\] Now substitute these numerical values into the first equation and solve for $E$ \[E=\frac{V}{d}=\frac{12}{2\times 10^{-3}}=6000\,\rm V/m\]

Energy Stored in a Capacitor: Problems

Problem (10): A capacitor of capacitance $29\,\rm pF$ in a vacuum has been charged by a $12\,\rm V$ battery. How much energy is stored in the capacitor?

Solution: Notice that in all capacitance problems, the energy is stored in the electric field between the plates. In this case, we can use one of the following three equivalent formulas to find the energy stored. \[U=\frac 12 CV^2=\frac{Q^2}{2C}=\frac 12 QV\] The capacitance and the voltage across the capacitor are given in the question, so substitute these into the first equation \begin{align*} U&=\frac 12 CV^2 \\\\ &=\frac{29\times 10^{-12}}{2(12)^2} \\\\ &=1.00\times 10^{-13}\,\rm J\end{align*}

Problem (11): The capacitance of an air-filled parallel-plate capacitor is $5\,\rm \mu F$. (a) How much energy is stored in the capacitor if it is connected to a $12\,\rm V$ battery?
(b) If the capacitor is disconnected from the battery and the distance between the charged plates is halved, how much energy is now stored in the capacitor?

Solution: (a) Substitute the given capacitance and voltage across the capacitor into the relevant formula below to find the energy stored: \begin{align*} U&=\frac 12 CV^2 \\ &=\frac 12 (5\times 10^{-6})(12)^2 \\ &=3.6\times 10^{-4}\, \rm J \end{align*} Hence, the energy stored is $0.36$ millijoules or $0.36\,\rm mJ$. The amount of charge deposited on each plate is also found to be \[Q=CV=(5\times 10^{-6})(12)=60\,\rm \mu C\]
(b) The capacitor is disconnected from the battery, so there is no agent to change the amount of charge on each previously charged plate. As a result, any changes in the geometry of the capacitor (say, plate separation, plate area) do not lead to a change in the accumulated charge on the plates.

Recall that according to the air-filled parallel plate capacitor formula, $C=\epsilon_0 \frac{A}{d}$, the capacitance is proportional to the plate area $A$ and inversely proportional to the plate separation $d$. Thus, the relation between old $C$ and new $C'$ capacitance is written as follows \[\frac{C'}{C}=\frac{d}{d'}=2 \] where we set $d'=\frac 12 d$. Hence, the capacitance after this change in the plate spacing becomes \[C'=2C=2\times 5=10\,\rm \mu F\] On the other hand, the initial charge on each plate does not change, $Q'=Q=60\,\rm \mu C$. Thus, it is more convenient to use the equation $U=\frac{Q^2}{2C}$ to find the energy stored in the new situation \begin{align*} U&=\frac{Q^2}{2C} \\\\ &=\frac{(60\times 10^{-6})^2}{2(10\times 10^{-6})} \\\\ &=0.18\ \rm mJ \end{align*} where $m=10^{-3}$. As you can see, by halving the distance between the two plates while the capacitor is disconnected from the source (battery), the energy stored in the capacitor decreases.

(c) After applying these changes to the capacitor, the battery is reconnected again to the capacitor. How much energy is stored in this case?
We saw that those changes in the geometry of the capacitor caused a change in its capacitance (in fact, the capacitance got doubled). Now that the battery is reconnect to this new capacitor, the energy stored in it is also changed by \begin{align*} U&=\frac 12 CV^2 \\ &=\frac 12 (10\times 10^{-6})(12)^2 \\ &=720\,\rm \mu J\end{align*} Thus, in this new configuration, the energy stored in the capacitor becomes $0.72\,\rm mJ$.

Problem (12): To move a charge of magnitude $0.25\,\rm mC$ from one plate of a $10\,\rm \mu F$ capacitor to another, we must take $2\,\rm J$ energy. How much charge is stored on each plate?

Solution:

Combinations of Capacitors

Problem (13): In the circuit below, find the following quantities:
(a) The equivalent capacitance of the circuit.
(b) The charge stored by this combination of capacitors.
(c) How much charge is stored in the $10-\rm \mu F$ capacitor?

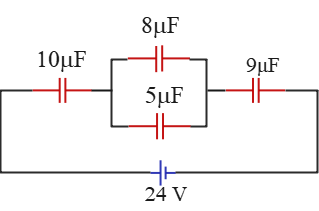
Solution: The two $5-\rm \mu F$ and $8-\rm \mu F$ capacitors are in parallel. When several capacitors are connected in parallel, their equivalent capacitance is the sum of their individual capacitances, i.e., $C_{eq}=C_1+C_2+\cdots$.

On the other hand, in the case of connecting several capacitors in series, the equivalent capacitance is obtained as below \[\frac{1}{C_{eq}}=\frac{1}{C_1}+\frac{1}{C_2}+\cdots\] But don't forget to inverse the result to find the equivalent capacitance.

(a) According to the above expression for capacitors in parallel, we have \[C_{5,8}=8+5=13\,\rm \mu F\] The newly obtained equivalent capacitor above are in series with the rest capacitors in the circuit. Thus, the overall equivalent capacitance of the given circuit is \[C_{eq}=13+9+10=32\,\rm \mu F\]
(b) In the previous part we found that the equivalent capacitance of the circuit is $32\,\rm \mu F$. This means we can replace all the original capacitors with a new one of value $32\,\rm \mu F$. The voltage across this capacitor is also $24\,\rm V$. Using the definition of capacitance, $C=\frac{Q}{V}$, and solving for $Q$, we will have \[Q=CV=(32\times 10^{-6})(24)=768\,\rm \mu C\] This is the total charge delivered by the battery and deposited on the $32\,\rm \mu F$ capacitor or distributed over the plates of the original capacitors.
(c) When several capacitors are connected in series with the voltage of the circuit, they equally store the total charge delivered by the battery. In this case, the two $10-\rm \mu F$ and $9-\rm \mu F$ capacitors are in series with the battery and hold equally the total charge of the circuit that is $768\,\rm \mu C$.

Problem (14): A $30-\rm \mu F$ capacitor is charged by a source of emf $24\,\rm V$. Then it is removed from the battery and is connected to a $25-\rm k\Omega$ resistor through which it discharges. After elapsing a time of $0.2\,\rm s$, Find (a) the charge and (b) the current in the circuit.

Solution: This circuit consists of a discharging capacitor and a resistor. As we learned in the RC circuit problems section, the charge and current in such circuits at any instant of time are given by the following formula \begin{gather*} q=q_0 e^{-\frac{t}{\tau}} \\\\ I=\frac{\mathcal E}{R}e^{-\frac{t}{\tau}} \end{gather*} where $\tau=RC$ is called time constant of the circuit and $\mathcal E$ is the emf of the battery. In this case, the time constant is \begin{align*} \tau&=RC \\ &=(25\times 10^3)(30\times 10^{-6}) \\&=750\times 10^{-3}\,\rm s\end{align*}
(a) In the first equation, $q_0=CV$ is the initial charge of the capacitor whose value is calculated as follows \[q_0=(30\times 10^{-6})(24)=720\,\rm \mu C\] Therefore, the charge of the capacitor at any moment is found to be \begin{align*} q&=q_0 e^{-\frac{t}{\tau}} \\\\ &=(720\times 10^{-6}) e^{-\frac{0.2}{0.750}} \\\\ &=551\times 10^{-6}\,\rm C\end{align*} Thus, after $0.2\,\rm s$ the charge stored in the capacitor reduces to $551\,\rm \mu C$.

(b) The electric current through the circuit is calculated from the second equation as below \begin{align*} I&=\frac{\mathcal E}{R} e^{-\frac{t}{\tau}} \\\\ &=\frac{24}{25\times 10^3} e^{-\frac{0.2}{0.750}} \\\\ &=0.735\,\rm mA\end{align*}

Author: Dr. Ali Nemati
Published: 3/9/2022