RC Circuit Problems with Solution for Students

In this post, we will practice solving problems involving RC series circuits. These problems are designed to be straightforward and beneficial for students preparing for the AP Physics C exams.

The topic of RC circuits can be divided into two sections: charging a capacitor through a resistor and discharging a capacitor through a resistor. For better understanding, we have separated these two parts.

RC Circuit: Charging Capacitor

Problem (1): An uncharged capacitor and a resistor are connected in series shown in the figure below. The battery's emf is $\mathcal E=12\,{\rm V}$, $C=8\,{\rm \mu F}$, $R=500\,{\rm k\Omega}$. After the switch is closed, find,
(a) The time constant of the RC circuit.
(b) The maximum charge on the capacitor.
(c) The charge on the capacitor 6 s after the switch is closed.

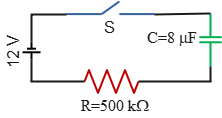
Solution: The capacitor is initially uncharged. After the switch is closed, the charge gradually accumulates on it through a resistor. This is an RC circuit for charging a capacitor.

(a) The time constant, $\tau$, for an RC circuit in a charging scenario, is defined as the time it takes for the charge on a capacitor to increase to about $63\%$ of its final charge. It is a measure of how quickly a capacitor charges. The time constant is given by: \[\tau=RC\] The SI unit of time constant is seconds $s$. Thus, the time constant of this RC series circuit is calculated as follows: \[\tau=\left(500\times 10^3\right)\left(8\times 10^{-6}\right)=4\,{\rm s}\] Hence, for this configuration, it takes about 4 seconds for the capacitor to reach $63\%$ of its final charge.

(b) The capacitor is initially uncharged, and the charge gradually accumulates on it through the resistor. The charge on the capacitor at any moment is given by the formula: \[Q=Q_f \left(1-e^{-t/\tau}\right)\] where $Q_f=C\mathcal{E}$ is the final charge. Thus, the amount of maximum charge on this capacitor is: \[Q_{max}=C\mathcal{E}=\left(8\times 10^{-6}\right)(12)=96\quad {\rm \mu C}\]

(c) After about 6 seconds have passed, the charge on the capacitor is calculated as follows: \begin{align*} Q&=Q_f \left(1-e^{-t/\tau}\right)\\\\&=96\left(1-e^{-6/4}\right)\\\\&=74.5\quad {\rm \mu C}\end{align*}

Read this, if you are getting ready for AP Physics 2 circuits:

AP Physics 2: Circuits practice problems with solution

Problem (2): In the following RC circuit, the total resistance is $20\,{\rm k\Omega}$, and the battery's emf is 12 V. Suppose the time constant of this RC circuit is $18\,{\rm \mu s}$. Find,
(a) The capacitance of the circuit.
(b) The time it takes the voltage across the resistor to reach 9 V after closing the switch.

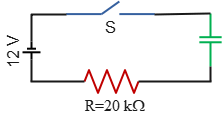
Solution: Because the source of emf is present in the circuit, the capacitor is initially uncharged and charges slowly.

The time constant in an RC circuit is defined as $\tau=RC$.

(a) Given the time constant, we can solve for the unknown capacitance: \[C=\frac{\tau}{R}=\frac{18\times 10^{-6}}{20\times 10^3}=9\times 10^{-10}\,{\rm F}\] So, the capacitance of the capacitor is $0.9\,{\rm nF}$.

(b) The potential difference across a charging capacitor in an RC circuit, which is proportional to the charge on it, is found using the formula: \[V=V_0 \left(1-e^{-t/\tau}\right)\] where $V_0$ is the battery's voltage or emf and $\tau$ is the time constant.

Here, the voltage at a later time is given, and the unknown quantity is time. Substituting the known numerical values into the formula gives: \begin{gather*} 6=9\left(1-e^{-t/18}\right)\\\\\frac{6}{9}=1-e^{-t/18}\\\\\Rightarrow e^{-t/18}=1-\frac 23=\frac 13\end{gather*} Note that we expressed the time constant in terms of $\mu s$ for simplicity, so the unknown time will also be in $\mu s$.

Now, taking the natural logarithms of both sides and solving for $t$: \begin{align*} \ln\left(e^{-t/18}\right)&=\ln\left(\frac 13\right)\\\\-\frac{t}{18}&=-1.09 \\\\\Rightarrow \quad t&=19.62\quad {\rm \mu s}\end{align*} Thus, after about $20\,{\rm \mu s}$, the voltage across the capacitor drops from 12 V to 9 V.

Problem (3): A 9-V battery is used to charge a $4-{\rm \mu C}$ capacitor through a resistor of $100\,{\rm \Omega}$. Find
(a) The initial current through the circuit.
(b) The final charge on the capacitor after completely being charged.
(c) The time it takes for the capacitor to reach $96\%$ its maximum charge.

Solution: In an RC series circuit, the first step is to find the time constant because all other quantities depend on it. The time constant is the product of the resistance and the capacitance: \[\tau=RC=(100)\left(4\times 10^{-6}\right)=0.4\,{\rm ms}\]

(a) When a capacitor is being charged in an RC circuit, the current at any instant of time is found using the formula: \[I=I_0 \left(1-e^{-t/\tau}\right)\] where $I_0=\frac{\mathcal E}{R}$ is the initial current in the circuit. So, \[I_0=\frac{\mathcal E}{R}=\frac{9}{100}=0.09\,{\rm A}\] Thus, the initial current is $90\,{\rm mA}$.

(b) In a capacitor charging case, the final charge on the capacitor is always given by $Q_{max}=C\mathcal E$. So, \[Q_{max}=\left(4\times 10^{-6}\right)(9)=36\quad{\rm \mu C}\]
(c) We are asked to find the unknown time $t$ at which the charge reaches $96\%$ of its final value, i.e., $Q_2=0.96Q_{max}$. The charge on the capacitor varies with time according to the formula: \[Q=Q_{max}\left(1-e^{-t/\tau}\right)\] Substituting the known values into the formula, we get: \begin{align*} Q&=Q_{max}\left(1-e^{-t/\tau}\right)\\\\0.96Q_{max}&=Q_{max}\left(1-e^{-t/0.4}\right)\\\\ \Rightarrow \quad e^{-t/0.4}&=1-0.96=0.04\end{align*} Now, taking the natural logarithms of both sides and solving for time $t$: \begin{gather*} \ln\left(e^{-t/0.4}\right)=\ln(0.04)\\\\-\frac{t}{0.4}=-3.22 \\\\\Rightarrow \quad t=1.288\,{\rm ms}\end{gather*} Hence, it takes about 1.3 ms for the capacitor to charge to $96\%$ of its final value.

Problem (4): An initially uncharged $8-{\rm \mu F}$ capacitor is placed in series with a resistance of $8\,{\rm \Omega}$ and a source of $12\,{\rm V}$. Find,
(a) The initial and final voltage across the resistor.
(b) The initial and final voltage across the capacitor.

Solution: Assume an uncharged capacitor in an RC circuit along with a switch. Just after closing the switch, the capacitor always behaves like a typical wire. Consequently, at this time $t=0$, there are only a resistor and a battery in the circuit. So, the voltage across the resistor is equal to that of the battery. Hence, at time $t=0$, we have: \[\Delta V_R=V_{battery}=12\,{\rm V}\]

Gradually, the charge is stored on the capacitor, creating a voltage drop across it. After a long time, when the capacitor is fully charged, the current through the resistor becomes zero. Using Ohm's law, $\Delta V_R=IR$, the voltage difference across the resistor is also zero.

(b) As mentioned above, at time $t=0$, immediately after closing the switch, the uncharged capacitor behaves like a wire. So, the voltage difference across it at this moment is zero.

After a long time, the current becomes zero, and thus the resistor is effectively removed from the circuit. Therefore, the voltage drop across the capacitor is the same as the source voltage. \[\Delta V_C= V_{battery}=12\,{\rm V}\]

Problem (5): In an RC circuit, there are two $4\,{\rm \mu F}$-uncharged capacitors, two $2.5\,{\rm k\Omega}$-resistors, and a source of 24 V. All these components are connected in series. After closing the switch,
(a) Find the initial current through the resistors.
(b) How long does it take the current to drop from its initial value to $2.4\,{\rm mA}$?

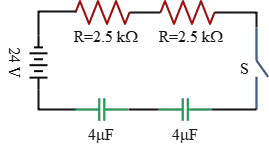
Solution: In an RC series circuit, we have one capacitor, one resistor, and one source. First, we must find the equivalent capacitance and resistance of the above circuit to convert it into one capacitor and one resistor.

The equivalent resistance of two resistors in series is the sum of their resistances, so: \[R=R_1+R_2=5\quad {\rm k\Omega}\] The equivalent capacitance of two capacitors in series is found using the formula: \[\frac 1C=\frac 1C_1+\frac 1C_2=2\left(\frac 14\right)=\frac 12\] Inverting the above gives the equivalent capacitance of two capacitors in series. So, $C=2\,{\rm \mu F}$.

(a) Just after closing the switch $S$, the capacitor doesn't have any charge, so it behaves like a typical wire. At this time, there are only a resistor and a source. Using Ohm's law formula, we can find the current through the resistor as \[I=\frac{V_0}{R}=\frac{24}{2.5\times 10^3}=0.0096\quad {\rm A}\] Thus, the initial current through the resistors is $9.6\,{\rm mA}$.

(b) In an RC series circuit, when the capacitor is being charged, the current reduces with time according to the formula: \[I=I_0e^{-t/RC}\] where $I_0$ is the initial current just after closing the switch.

The current at the unknown time $t$ is given as 2.4 mA. Substituting this into the formula, we have: \[2.4=9.6e^{-t/RC}\] where we used the initial current $I_0=9.6\,{\rm mA}$ computed in part (a).

Now, taking the natural logarithm of both sides and solving for the time $t$: \begin{gather*} \ln\left(\frac{2.4}{9.6}\right)=\ln e^{-t/RC}=-\frac{t}{RC}\\\\ \Rightarrow \quad t=1.38RC\end{gather*} where $\tau=RC$ is the time constant of an RC circuit. The time constant of this circuit is \[\tau=(5000)\times \left(2\times 10^{-6}\right)=0.01\,{\rm s}\] Thus, the time it takes for the current to drop from initially 9.6 mA to 2.4 mA is: \[t=1.38\tau=1.38\times 0.01=13.8\,{\rm ms}\]

RC Circuit: Discharging Capacitor

Problem (6): A $5\,{\rm \mu F}$-capacitor is charged to a 12 V and then connected to a $400\,{\rm \Omega}$-resistor. Find,
(a) The time constant of this RC circuit.
(b) The initial charge stored on the capacitor.
(c) The initial current through the resistor.
(d) The charge on the capacitor after 3 ms.

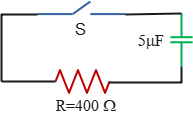
Solution: A fully charged capacitor is connected to a resistor and consequently discharges through it. In this case, there is no battery in the circuit.

(a) The time constant, $\tau=RC$, is the time it takes for the charges on the capacitor to decrease to about $37\%$ of its initial charges. For this RC circuit, we have \[\tau=400 \times \left(5\times 10^{-6}\right)=2\times 10^{-3}\,{\rm s}\] Thus, the time constant of this RC circuit is $2\,{\rm ms}$.

(b) Just after closing the switch, the initial charge on the capacitor is: \[Q_0=CV_0=\left(5\times 10^{-6} \right)(12)=60\,{\rm \mu C}\]
(c) When a capacitor in an RC series circuit is discharging, the current at any moment is determined by the following formula: \[I=I_0 e^{-t/\tau}\] where $I_0=\frac{V_0}{R}$ is the initial current at time $t=0$. Thus, \[I_0=\frac{V_0}{R}=\frac{12}{400}=0.03\quad {\rm A}\] Multiplying by $1000$ gives the current in milliamperes. So, $I_0=30\,{\rm mA}$.

(d) In the discharging case, the charge on the capacitor varies with time as $Q=Q_0e^{-t/RC}$. So, after $t=3\,{\rm ms}$, the amount of remaining charge is: \begin{align*} Q&=Q_0e^{-t/RC}\\\\&=\left(60\times 10^{-6}\right)e^{-\frac{3}{2}}\\\\&=13.38\,{\rm \mu C}\end{align*}

Problem (7): A $C=4\,{\rm \mu F}$-capacitor is charged to a source of $\mathcal{E}=24\,{\rm V}$ and then connected to a resistor of $R=200\,{\rm \Omega}$ in series. After the switch is closed, find
(a) The initial current through the resistor.
(b) The current after passing two time constants.
(c) The time constant of the circuit.

Solution: After closing the switch, the capacitor discharges (loses its charges) through the resistor. Recall that the time rate of change of electric charge is defined as current.

The exact form of this variation with time is given by $I=I_0e^{-t/RC}$, where $I_0=\frac{\mathcal{E}}{R}$ is the initial current in the RC circuit.

(a) Immediately after closing the switch, the current in the RC circuit is found using the following formula: \[I_0=\frac{\mathcal{E}}{R}=\frac{24}{200}=0.12\,{\rm A}\]
(b) The capacitor is discharging, so the current at any instant of time in the RC circuit is determined by $I=I_0e^{-t/\tau}$, where $\tau=RC$ is the time constant of the circuit.

Thus, the current after 2 time constants, $t=2\tau$, is \begin{align*} I&=I_0e^{-t/RC}\\\\&=0.12\,e^{-2\tau/\tau}=0.0162\quad {\rm A}\end{align*} Hence, after 2 time constants, the current is about 16.2 mA.

The time constant is calculated as follows: \[\tau=200\times \left(4\times 10^{-6} \right)=8\times 10^{-4}\,{\rm s}\] This is the time duration in which the charge on the capacitor decrease to about $37\%$ of its initial charges.

Problem (8): Suppose an RC series circuit with a capacitor of $5\,{\rm \mu F}$, a resistor of $80\,{\rm k\Omega}$, and an initial voltage difference across the capacitor of $6\,{\rm V}$.
(a) Find the time constant of this RC circuit.
(b) How long does it take the capacitor to lose half its initial charge?
(c) How long does it take the capacitor to lose $99.99\%$ of its initial charge?

Solution: The capacitor has an initial voltage across itself, so it is fully charged initially and discharges through the resistor slowly.

(a)The time constant $\tau$ for a discharging capacitor in an RC circuit tells us how much time is required for the charge on the capacitor to decrease to about $37\%$ of its initial value.

In an RC series circuit, the product of the resistance $R$ and the capacitance $C$ is defined as a time constant. So, \[\tau=RC=\left(80\times 10^3\right)\left(5\times 10^{-6}\right)=0.4\,{\rm s}\]
(b) “How long” means the time is unknown. Let the initial charge be $Q_0$. We want to find the time when the charge is $Q=(0.5)Q_0$.

Recall that for a discharging capacitor the charge at any instant of time is given by the formula: \[Q=Q_0 e^{-t/\tau}\] Substituting the known values, we get: \begin{align*} 0.5Q_0 &=Q_0 e^{-t/0.4}\\\\ \ln(0.5)&=\ln\left(e^{-t/0.4}\right)=-\frac{t}{0.4}\\\\ \Rightarrow \quad t&=(0.4)\ln(0.5)\\\\&=0.277\quad{\rm s}\end{align*} Hence, it takes about 0.3 s for the charge on the capacitor to become half its initial value.

(c) "loses $99.99\%$ of its initial value'' means that the remaining charge on the capacitor is only $1-0.9999$ of its initial value, i.e., $Q=0.0001Q_0$. So, \begin{align*} 0.9999Q_0 &=Q_0 e^{-t/0.4}\\\\ \ln(0.0001)&=\ln\left(e^{-t/0.4}\right)=-\frac{t}{0.4}\\\\ \Rightarrow \quad t&=(0.4)\ln(0.0001)\\\\&=3.684\quad{\rm s}\end{align*} This calculation gives us an estimate of how long it takes for the capacitor to be almost completely discharged.

Problem (9): A $150\,{\rm \mu F}$-capacitor is charged to a 1500 V and then connected in series with an unknown resistor. It is observed that the capacitor loses $95\%$ of its charge in 50 ms. Find the resistance of the resistor.

Solution: The capacitor is fully charged initially and then discharges through the resistor. In this case, the initial charge $Q_0$ on the capacitor decreases with time according to the formula: \[Q=Q_0 e^{-t/RC}\] where $Q$ is the charge on the capacitor at any instant of time.

It is stated in the question that after 50 ms, the capacitor loses $95\%$ of its initial charge. This means that after this time duration, the charge on the capacitor is only $5\%$ of its initial charge, i.e., $Q=0.05Q_0$. So, we have \begin{align*} Q&=Q_0 e^{-t/RC}\\\\ 0.05Q_0&=Q_0 e^{-t/RC}\\\\0.05&=e^{-t/RC}\end{align*} Taking the natural logarithm and solving for the unknown resistance $R$, we get: \begin{align*} \ln (0.05)&=\ln\left(e^{-t/RC}\right)=-\frac{t}{RC}\\\\ \Rightarrow \quad R&=-\frac{t}{C\ln(0.05)}\\\\ &=-\frac {50\times 10^{-3}}{\left(150\times 10^{-6}\right)\times \ln(0.05)}\\\\ &=111.26 \quad {\rm \Omega} \end{align*}

Problem (10): In an RC series circuit, a capacitor C is being discharged through a resistor of R. How long does it take for the charge on the capacitor to drop to one-third its initial value?

Solution: "How long'' refers to the time duration. In an RC circuit with a discharging capacitor, the charge on the capacitor at any instant of time is given by the formula: \[Q=Q_0 e^{-t/RC}\] where $Q_0$ represents the maximum (initial) charge. We want to find the time when $Q=\frac 13 Q_0$. Substituting this relation into the formula, we have: \begin{gather*} Q=Q_0e^{-t/RC}\\\\\frac 13 Q_0=Q_0e^{-t/RC}\\\\ \frac 13 =e^{-t/RC}\end{gather*} Now, taking the natural logarithms of both sides and solving for the unknown time $t$: \begin{gather*} \ln\left(\frac 13\right)=\ln e^{-t/RC}=-\frac{t}{RC}\\\\ \Rightarrow t=-RC\ln\left(\frac 13\right)=1.79RC\end{gather*} Thus, after approximately 1.8 time constants $\tau$, the charge on the capacitor reaches one-third of its initial value. (recall that the time constant is defined as $\tau=RC$)

Summary:

In this article, we explored how to solve simple RC circuit problems. We began by calculating the time constant of the RC circuit, $\tau=RC$, and then applied the appropriate charging and discharging formulas to find the desired quantities.

RC Circuit Problems with Solution for Students

RC Circuit: Charging Capacitor

RC Circuit: Discharging Capacitor

Summary:

Other related topics: