Doppler Effect Problems with Solutions for College Physics

Here, you can solve some problems related to the Doppler effect in college physics. The solutions are presented in a comprehensive and self-taught manner.

Introduction:

When there is relative motion between a sound source (or other wave types) and an observer, the pitch (frequency) that the observer hears varies according to the formula \[f_O=\frac{v\pm v_O}{v\pm v_S} f_S\] where $\rm O$ and $\rm S$ stand for observer and source, respectively and $v$ represents the speed of sound in still air.

In all Doppler effect questions, the most important thing about the formula above is recognizing when to use a positive or negative sign for the velocities of the source and the observer.

Always draw an arrow pointing from the source toward the observer (receiver) and take this direction as a reference.

If the observer or source velocities are in this direction, then we must select the negative sign in the above formula for both; otherwise, the positive sign is substituted.

In the following, practice some practice problems to master this topic.

Doppler Effect Problems

Problem (1): The siren of a police car moving at a constant speed of $30\,\rm m/s$ emits a wave with a frequency of $1200\,\rm Hz$. What frequency will an individual at rest hear when the police car moves (a) toward her, or (b) away from her? The speed of sound is $340\,\rm m/s$, and the air is still.

Solution: (a) Consider the following figure in which a police car with a siren approaches a person at rest from the left.

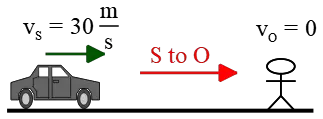
A siren approaching to an observer at rest in the Doppler effect problem

Draw a vector from the siren to the person. This vector serves as the reference direction for our problem.

The police car's velocity is in this direction, so we must choose the positive sign for the velocity of the police car.

On the other hand, the person (or observer) is at rest, so $v_O=0$. Substituting these numerical values into the given formula, we get: \begin{align*} f_O &=\frac{v\pm v_O}{v\pm v_S} f_S \\\\ &=\frac{v}{v-v_S}f_S \\\\ &=\frac{340}{340-30}(1200) \\\\ &\approx 1316\quad \rm Hz \end{align*} Thus, if a siren emitting a frequency of $1200\,\rm Hz$ approaches a person at rest with a velocity of $30\,\rm m/s$, the person hears a sound with a frequency of about $1316\,\rm Hz$.

(b) Now, let’s consider the scenario where the siren is moving away from the observer, say toward the right.

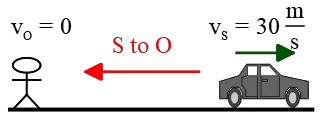
A siren receding an observer at rest in the Doppler effect problem

Draw a vector from right to left and compare the sign of all other velocities with this direction. In this case, the siren's velocity is in the opposite direction of this vector, so we must choose a positive sign for its speed.

Before solving, we expect a lower pitch (frequency) to be perceived by the person. Using the same formula, where the values remain the same, we find: \begin{align*} f_O &=\frac{v\pm v_O}{v\pm v_S} f_S \\\\ &=\frac{v}{v+v_S}f_S \\\\ &=\frac{340}{340+30}(1200) \\\\ &\approx 1102\quad \rm Hz \end{align*} As expected, the perceived frequency is lower when the siren moves away from the observer.

Problem (2): A sound wave of frequency $525\,\rm Hz$ is emitted by a stationary source toward an observer who is moving away with a constant speed of $25\,\rm m/s$.
(a) What is the frequency perceived by the observer?
(b) Calculate the wavelength of the sound as measured by the source and the observer.

Solution: Given the following information:
Source frequency $f_S=525\,\rm Hz$
Source's speed $v_S=0$
Observer's speed $v_O=25\,\rm m/s$
Sound speed in still air $v=340\,\rm m/s$

(a) Assume the observer is moving toward the right. The vector from the source to the observer is to the right, in the same direction as the observer's velocity. Hence, we include a minus sign for $v_O$ in the Doppler effect formula. \begin{align*} f_O&=\frac{v\pm v_O}{v\pm v_S} f_S \\\\ &=\frac{v-v_O}{v}f_S \\\\ &=\frac{340-25}{340} 525 \\\\ &\approx 486 \quad \rm Hz \end{align*} As expected, since the observer is moving away from a source at rest, the detected frequency is lower than the original emitted frequency by the source.

(b) The three main characteristics of a wave—wavelength, frequency, and wave speed— are related by: \[\lambda=\frac{v}{f}\] According to this equation, the wavelength that the source at rest measures for its emitting sound wave is: \[\lambda_S=\frac{v}{f_S}=\frac{340}{525}=0.65\,\rm m\] This is approximately equal to $\lambda_S=65\,\rm cm$.

On the other hand, the wavelength measured by the moving observer is: \[\lambda_S=\frac{v}{f_S}=\frac{340}{486}=0.70\,\rm m\] This corresponds to about $\lambda_O=70\,\rm cm$.

Problem (3): Suppose a police car is at rest and emits at $1200\,\rm Hz$. What frequency would a person hear if he were moving at $30\,\rm m/s$ (a) toward it or (b) away from it?

Solution: This problem presents the opposite scenario from the previous one. Here, the siren (emitter) is at rest, while the person (receiver) is in motion.
(a) Suppose the person is moving toward the siren from the left, as depicted in the figure below.

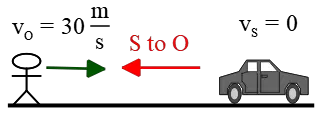
An observer is approaching to a siren at rest in the Doppler effect problem

Draw a vector from the siren to the person (in this case, in the negative $x$ direction). Since the siren is stationary, we have $v_S=0$.

The person's velocity is opposite to the reference vector, so it must be included with a positive sign in the Doppler effect formula. Substituting the numerical given values: \begin{align*} f_O &=\frac{v\pm v_O}{v\pm v_S} f_S \\\\ &=\frac{v+v_O}{v}f_S \\\\ &=\frac{340+30}{340}(1200) \\\\ &\approx 1305\quad \rm Hz \end{align*} As expected, when an approaching person moves toward a stationary siren, an increase in the original emitted frequency is perceived.

(b) Now, let’s consider the case where the person is moving away from the siren (which is still at rest) and is positioned on the right side of it.

An observer is receding a siren at rest in the Doppler effect problem

The vector pointing from the siren to the moving person is toward the right, aligning with the person's travel direction.

Thus, the person's velocity, $v_O$, must be included with a negative sign in the formula: \begin{align*} f_O &=\frac{v\pm v_O}{v\pm v_S} f_S \\\\ &=\frac{v-v_O}{v}f_S \\\\ &=\frac{340-30}{340}(1200) \\\\ &\approx 1094\quad \rm Hz \end{align*} As expected, this frequency corresponds to a moving receiver (person) who is now away from the static emitting source.

Problem (4): The siren of a police car moving away from a person at a speed of $35\,\rm m/s$ emits at $550\,\rm Hz$. The person is also moving toward the siren at a speed of $5\,\rm m/s$. Assume the speed of sound in the air to be $340\,\rm m/s$. What frequency would the person hear?

Solution: In this Doppler effect problem, both the source and listener (receiver) are in motion. Let’s assume the siren is moving to the right. The vector pointing from the source (siren) to the listener (receiver) is toward the left, and we refer to this as the reference vector.

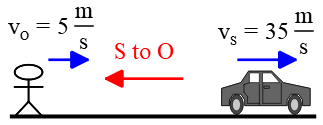
Both the source and the observer are moving in the same direction

The siren and the listener (observer) are traveling in the opposite direction of the reference vector. Therefore, we choose positive signs for their velocities.

Taking all these considerations into account, we have: \begin{align*} f_O &=\frac{v\pm v_O}{v\pm v_S} f_S \\\\ &=\frac{v+v_O}{v+v_S}f_S \\\\ &=\frac{340+5}{340+35}(550) \\\\ &=506\quad \rm Hz \end{align*} Let's check our numerical result. Both the siren and the person are moving to the right, but the person’s speed is slower than that of the car. Consequently, the siren is gradually moving away from the person.

As expected, the person will hear a reduction in the original frequency emitted by the siren, consistent with our calculated value.

Problem (5): Two cars are moving (a) toward each other, (b) away from each other. The car $1$ has a speed of $120\,\rm km/h$ while the car $2$ moves at $95\,\rm km/h$. Assume car $1$ blows its horn and emits a sound at a frequency of $400\,\rm Hz$. What frequency is heard by the driver of the car $2$?

Solution: Given that both cars are moving at different velocities in kilometers per hour $\rm km/h$, we need to convert them to SI units (meters per second) to use them in the Doppler effect formula: \begin{gather*} v_1=120\times \frac{1000}{3600}\approx 33 \,\rm m/s \\\\ v_2=95\times \frac{1000}{3600}\approx 26 \,\rm m/s \end{gather*}
(a) Both cars are moving toward each other, as shown in the figure below. In this problem, car $1$ is assumed to be the source, and the other car is the observer (receiver).

The vector extending from the source to the receiver is to the right (red arrow in the figure). Cars $1$ and $2$ move in the same and opposite directions of the reference vector, respectively. Hence, they must be included with a negative and a positive sign in the formula, respectively.

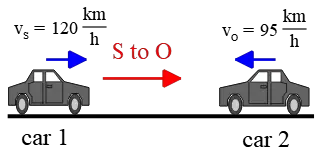
Both the source and the observer are moving toward each other.

Substituting the numerical values into the known formula gives the frequency heard by the driver of car $2$ (receiver) as: \begin{align*} f_O &=\frac{v\pm v_O}{v\pm v_S} f_S \\\\ &=\frac{v+v_O}{v-v_S}f_S \\\\ &=\frac{340+26}{340-33}(400) \\\\ &\approx 477 \quad \rm Hz \end{align*} As expected.

(b) Now, let’s consider the case where the two cars are moving away from each other, as depicted in the figure below:

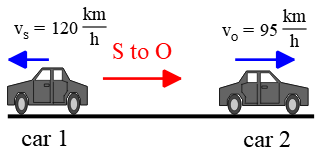
Both the source and the observer are moving away from each other.

Again, the reference vector extends from car $1$ (source) to car $2$ (observer), which is toward the right.

Car $1$ (source) moves in the opposite direction, but car $2$ moves in the same direction as this reference vector.

Thus, the speed of car $1$ (source) is entered with a positive sign in the formula, and the speed of car $2$ (observer) is accompanied by a negative sign. \begin{align*} f_O &=\frac{v\pm v_O}{v\pm v_S} f_S \\\\ &=\frac{v-v_O}{v+v_S}f_S \\\\ &=\frac{340-26}{340+33}(400) \\\\ &\approx 335 \quad \rm Hz \end{align*}

Problem (6): Suppose you are standing by a railway. You record the train whistle at $554\,\rm Hz$ when the train is approaching you, and $356\,\rm Hz$ when the train is moving away from you. How fast does the train move? (Take the speed of sound in air to be $v=340\,\rm m/s$).

Solution: This is a slightly more challenging Doppler effect problem because we need to apply the Doppler effect formula twice. The problem is depicted in the following figure. The person (receiver or listener) is at rest, $v_O=0$, while a train approaches and receives him/her at different frequencies.

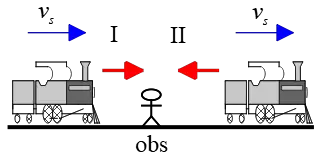
An observer at rest and source is approaching and receding.

Let $f_{O-I}$ and $f_{O-II}$ be the recorded frequencies by the person when the train is approaching and receding, respectively.

When the train approaches, the vector from the source to the observer points to the right (indicated by the red arrow), aligning with the source velocity.

Thus, the frequency perceived by the person can be calculated as: \begin{align*} f_{O-I} &=\frac{v\pm v_O}{v\pm v_S} f_S \\\\ &=\frac{v}{v-v_S}f_S \end{align*} where $f_S$ is the original frequency emitted by the train whistle (source).

In the receding scenario, the vector from the source to the observer points to the left, opposing the source velocity.

Thus, We choose a positive sign for $v_S$. \begin{align*} f_{O-II} &=\frac{v\pm v_O}{v\pm v_S} f_S \\\\ &=\frac{v}{v+v_S}f_S \end{align*} Dividing these two expressions by each other and canceling the common factors, gives us a relation in which the speed of the train is unknown. \[\frac{f_{O-I}}{f_{O-II}}=\frac{v+v_S}{v-v_S}\] Substituting the numerical values into this and solving for $v_S$ gives \begin{gather*} \frac{554}{356}=\frac{340+v_S}{340-v_S} \\\\ 554(340-v_S)=356(340+v_S) \\\\ 340(554-356)=v_S(356+554) \\\\ \Rightarrow \boxed{v_S\approx 74\,\rm m/s} \end{gather*} Hence, the train approaches the person at a constant speed of $74\,\rm m/s$ and subsequently moves away from him.

Problem (7): Two car horns each have a frequency of $375\,\rm Hz$. A stationary person is between them and is moving toward the right at a speed of $10\,\rm m/s$. Suppose the car $A$ is at rest while the car $2$ is moving toward the right (and away from the observer) with a speed of $25\,\rm m/s$.
(a) What is the frequency of $A$ heard by the person?
(b) What frequency is heard from $B$ by the person?
(c) What is the beat frequency counted by the observer?

Solution: The entire problem is illustrated in the following figure.

First, on both sides, draw vectors (called reference vectors) pointing from the source to the observer (person). On the left side, this vector points to the right, and on the right side, it points toward the left.

(a) Calculate the frequency detected by the person from car $A$ (source) using the Doppler effect equation: \begin{align*} f_{S_A} &=\frac{v\pm v_O}{v\pm v_{S_A}} f_{S_A} \\\\ &=\frac{v-v_O}{v}f_{S_A} \\\\ &=\frac{340-10}{340}(375) \\\\&\approx 364\,\rm Hz \end{align*} Since the reference vector and the person's velocity are in the same direction, choose a minus sign for $v_O$ in this part of the problem.

(b) In this section, both the person (receiver or listener) and the source (car's horn) are moving in the same direction.

However, the reference vector points to the left, opposing the source and the person, so a positive sign should be chosen for the velocities of the person (listener) and the source. \begin{align*} f_{O_B} &=\frac{v\pm v_O}{v\pm v_{S_B}} f_{S_B} \\\\ &=\frac{v+v_O}{v-v_{S_B}}f_{S_B} \\\\ &=\frac{340+10}{340+25}(375) \\\\&\approx 360\,\rm Hz \end{align*} As expected, because the velocity of car $B$ is greater than that of the person, the source gradually moves away from the observer, resulting in a lower pitch (frequency).

(c) This part relates to a beat frequency problem. Recall that the interference (or superposition) of two waves with slightly different frequencies produces a new wave with a varying loudness over time.

The beat frequency is given by: $f_{beat}=|f_2-f_1|$. Note that the absolute value of the difference between frequencies matters for finding the beat frequency. Substituting the numerical values into the above formula gives: \[f_{beat}=|360-364|=4\,\rm Hz\]

Problem (8): Suppose you hold a tuning fork vibrating at $245\,\rm Hz$ and are moving toward a wall with a constant speed of $6\,\rm m/s$. What frequency do you hear when the wave is reflected backward?

Solution: This problem consists of two parts.

Part 1: Approaching the Wall: You, as the source (emitter), are approaching the wall, which acts as the receiver (observer). The vector pointing from the source to the observer is toward the right as shown in the figure below.

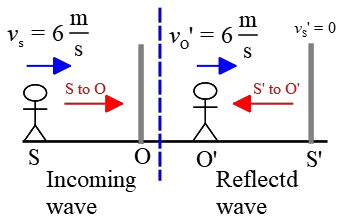
Beat frequency in echo sound waves in the Doppler effect problem

Since the source's velocity and this vector are in the same direction, we choose $v_S$ to be negative. \begin{align*} f_O &=\frac{v\pm v_O}{v\pm v_S} f_S \\\\ &=\frac{v}{v-v_S}f_S \\\\ &=\frac{v}{v-6}f_S \end{align*} where $f_S$ represents the frequency at which the tuning fork vibrates, and $f_O$ is the frequency received by the wall.

Part 2: Echo Formation: When the sound wave reflects back from the wall (creating an echo), the wall acts as an emitter (source) of a wave with a frequency of $f_{S'}$.

The original source (you in the first part) becomes the new observer (receiver) and perceives a frequency of $f_{O'}$.

Draw a vector from this new source to the new observer, pointing to the left. Since the new observer moves in the opposite direction of this vector, we use a positive value for $v_{O'}$. \begin{align*} f_{O'} &=\frac{v\pm v_{O'}}{v\pm v_{S'}} f_{S'} \\\\ &=\frac{v+v_{O'}}{v}f_{S'} \\\\ &=\frac{v+6}{v}f_{S'} \end{align*} where $f_{S'}$ is the frequency of the wave which is reflected back from the wall.

It is clear that the incoming frequency $f_O$ (in part $1$) and the reflected back frequency $f_{S'}$ (in part $2$) are the same; $f_O=f_{S'}$.

The frequency of a wave remains unchanged upon striking a barrier, so the incoming and reflected waves have identical frequencies.

By combining the two above expressions, we arrive at the final expression: \begin{gather*} f_{O'}=\frac{v+v_{O'}}{v}\times \frac{v}{v-v_S} f_S \\\\ \Rightarrow \boxed{f_{O'}=\frac{v+v_{O'}}{v-v_S} f_s} \end{gather*} Substituting the numerical values and solving for the echo frequency heard by the person $f_{O'}$, we find \begin{align*} f_{O'}&=\frac{v+v_{O'}}{v-v_S} f_s \\\\ &=\frac{340+6}{340-6}(245) \\\\ &\approx 254\quad \rm Hz \end{align*}

Problem (9): Suppose the horn frequency of two cars is the same. One is at rest, and the other is traveling toward the first at a constant speed of $25\,\rm m/s$. In this situation, the driver at rest detects a beat frequency of $3.5\,\rm Hz$. What frequency do the horns emit?

Solution: The difference between two nearly equal frequencies is called the beat frequency, denoted as $f_{beat}=|f_1-f_2|$, where $|\cdots|$ represents the absolute value of the subtraction.

The stationary driver detects its own original horn frequency but hears a changed frequency for the other car. Our task is to find this changed frequency detected by the driver at rest.

The stationary driver is considered to be an observer ($v_O=0$) and hears a frequency of $f_O$. The other driver, then, is an emitter having a velocity of $v_S=25\,\rm m/s$ and emitting a sound of frequency $f_S$.

According to the Doppler effect, $f_O$ is calculated by \[f_O =\frac{v\pm v_O}{v\pm v_S} f_S =\frac{v}{v-v_S} \] This is the frequency that the driver at rest hears from the other car. The difference between this frequency and its own horn frequency gives the beat frequency. \begin{align*} f_{beat}&=|f_O-f_S| \\\\ &=\left|\frac{v}{v-v_S}f_S-f_S \right| \\\\ &=f_S\left|\frac{v}{v-v_S}-1\right| \\\\ &=f_S \left|\frac{v_S}{v-v_S}\right| \end{align*} Substituting the numerical values into it and solving for the original horn frequency of these two cars yields \begin{gather*} f_{beat}=\frac{v_S}{v-v_S} f_S \\\\ 3.5=\frac{25}{340-25} f_S \\\\ \rightarrow (3.5)(340-25)=25f_S \\\\ \Rightarrow \boxed{f_S=44.1\,\rm Hz} \end{gather*} where in the above, we omitted $|\cdots|$ since the result is positive.

Problem (10): Suppose the frequency of a car's horn at rest is $350\,\rm Hz$. The car's driver sounds this horn, while it is moving. A bicyclist moving in the same direction as the car with one-fourth the car's speed hears a frequency of $325\,\rm Hz$. (a) Is the bike moving in front of or behind the car? (b) What is the speed of the car?

Solution: (a) To determine whether the bike is ahead of or behind the car, let's consider each case separately.

Bike Ahead of the Car: Assume the bike is moving at one-fourth the car's speed ahead of the car.

Since the car is faster than the bike, it gradually catches up to the bike.

In this scenario, we would expect to hear an increasing frequency, similar to when an ambulance approaches.

However, this is not the case, as the frequency heard by the cyclist is lower than that of the car.

Bike Behind the Car (Correct Result): Because the bike moves slower than the car, it is always getting further away from the car. Consequently, the cyclist hears a lower pitch (frequency).

(b) The actual situation is depicted in the following figure.

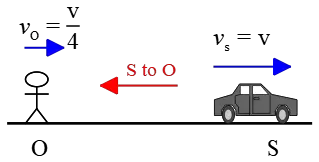
The source and the observer are moving in the same direction with different velocities.

The car serves as the source, and the bike acts as the observer.

The vector pointing from the source to the observer provides a hint for determining the sign in the Doppler effect formula.

In this case, the vector points to the left.

Both the car and the bike move in the opposite direction of this vector. Therefore, we include a positive sign for $v_S$ and $v_O$. \begin{gather*} f_O =\frac{v\pm v_O}{v\pm v_S} f_S \\\\ f_O=\frac{v+v_O}{v+v_S} f_S \end{gather*} Assumming the car's speed is $v_S=v$, the bike's speed becomes $v_O=\frac 14 v$. Substituting the given numerical values into the formula and solving for $v$, we find: \begin{gather*} 325=\frac{340+\frac 14 v}{340+v} 350 \\\\ \Rightarrow \boxed{v\approx 36\,\rm m/s} \end{gather*}

Summary:

In this article, we delve into solving Doppler effect problems step by step, providing detailed solutions. Let’s highlight the key steps for tackling these questions effectively:

Identify the Source and Observer:

Begin by recognizing the roles of the source (emitter) and the observer.
Draw a vector from the source to the observer, indicating the direction of the sound wave.

Reference Vector and Sign Selection:

Pay attention to the velocities involved (source velocity ($v_S$) and observer velocity ($v_O$)) in the Doppler effect formula.
If these velocities align with the reference vector (i.e., they are in the same direction), choose a minus sign.
Conversely, if they oppose the reference vector, use a positive sign: \[ f_O = \frac{v}{v - v_S} f_S \]

where $v$ is the speed of the sound wave. $f_O$ and $f_S$ are the frequencies heard by an observer and the frequency emitted by a source, respectively.

Author: Dr. Ali Nemati
Published: 4/9/2022