Electric Force: Problems and Solutions for AP Physics C
Here, a number of problems about electric force are answered that are useful for AP Physics C exams. All these solved problems are similar to Coulomb's law problems so you can practice those for further understanding.
Electric Force Problems:
Problem (1): Object A has a charge of $-3\,{\rm \mu C}$ and a mass of $0.0025\,{\rm kg}$. Object B has a charge and a mass of $+1\,{\rm \mu C}$ and 0.02 kg respectively. What is the magnitude of the electric force between the two objects when they are $0.3$ meters away?
Solution: the magnitude of the electric force between two charged particles which are at distance of $d$ are found by the Coulomb's law formula \[F_e=k\frac{|q_1 q_2|}{d^2}\] where $k=8.99\times 10^{9}\,{\rm N.m^{2}/C^{2}}$ is the Coulomb constant.
$|\cdots|$ indicates the absolute values of the charges meaning without their signs. Thus, \begin{align*}F_e&=k\frac{|q_1 q_2|}{d^2}\\ \\ &=(8.99\times 10^{9})\frac{(3\times 10^{-6})(1\times 10^{-6})}{(0.3)^2}\\ \\&=0.299\quad {\rm N}\end{align*}
Problem (2): Two point charges of $3\,{\rm nC}$ each are separated by $6\,{\rm cm}$. What is the magnitude of the electric force exerted by one of the charges on the other one?
Solution: The two point charges, here, have the same sign so there is a repulsive force between them whose magnitude is calculated by Coulomb's law formula \begin{align*}F_e&=k\frac{|q_1 q_2|}{d^2}\\ \\ &=(8.99\times 10^{9})\frac{(3\times 10^{-9})(3\times 10^{-9})}{(0.06)^2}\\ \\&=22.5\times 10^{-6}\quad {\rm N}\end{align*} Thus, these two point charges, spaced $0.06\,\rm m$, are repelled each other with a force of about $22.5\,\rm \mu N$. This is a very small force.
Problem (3): Three point charges are positioned along a straight line on the $x$ axis as: $q_1=-2\,{\rm \mu C}$ is at $x=-2\,{\rm m}$, $q_2=-4\,{\rm \mu C}$ is at origin, and $q_3=+3\,{\rm \mu C}$ is at $x=+4\,{\rm m}$. Find the electric force on charge $q_3$.
Solution: There are two electric forces acting on the charge $q_3$.
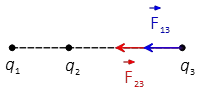
The magnitude of the force $F_{13}$ exerted by $q_1$ on $q_2$ is determined as \begin{align*}F_{13}&=k\frac{|q_1 q_3|}{d^2}\\ \\ &=(8.99\times 10^{9})\frac{(2\times 10^{-6})(3\times 10^{-6})}{6^2}\\ \\ &=1.5\quad {\rm mN}\end{align*}Since the charges are unlike so they attract and the force is in the $-x$ direction that is \[\vec{F}_{13}=-1.5\times 10^{-3}\,{\rm N}\,(\hat{i})\] Similarly, the magnitude of the force $F_{23}$ exerted by $q_2$ on $q_3$ is also determined as \begin{align*}F_{23}&=k\frac{|q_2 q_3|}{d^2}\\ \\ &=(8.99\times 10^{9})\frac{(4\times 10^{-6})(3\times 10^{-6})}{4^2}\\ \\ &=6.75\quad {\rm mN}\end{align*}Charges have the opposite signs, so they attract and the force is in the $-x$ axis. \[\vec{F}_{23}=-6.75\times 10^{-3}\,{\rm N}\,(\hat{i})\] To find the resultant electric force on the charge $q_3$, we must vector sum individual forces exerted on the charge $q_3$. This is the principle of the superposition of forces. Therefore, \begin{align*} \vec{F}_3 &=\vec{F}_{13}+\vec{F}_{23}\\ &=-(8.25\, {\rm mN})\,\hat{i}\end{align*}
Problem (4): Three point charges, each of magnitude $3\,{\rm nC}$, sit on the corners of a right triangle as in the figure below. Find the direction and magnitude of the electric force on the charge $q_3$.
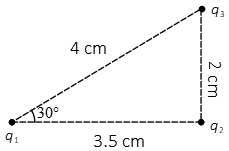
Solution: First, find the individual forces acting on the desired charge. Next, the vector sum of those forces to find the net force on that charge. The magnitude of the electric force is given by Coulomb's law.
The magnitude of the force exerted by charge $q_1$ on charge $q_3$ is \begin{align*} F_{13}&=k\frac{|q_1q_3|}{d_{13}^2}\\ \\ &=\frac{(8.99\times 10^{9})(3\times 10^{-9})^2}{4^2}\\ \\ &=5.06\times 10^{-9}\quad {\rm nC}\end{align*} Since the charges have the same sign so they repel each other.
Recall that according to Coulomb's law, the electric force between two charges is along the line connecting them. In this case, the force is directed away from charge $q_3$ and makes an angle of $30^\circ$ with the horizontal. Therefore, the force $F_{13}$ has the following components \begin{align*} \vec{F}_{13}&=F_{13}\cos \theta\,\hat{i}+F_{13}\sin \theta\, \hat{j}\\ &=(5.06\times 10^{-9})(\cos 30^\circ\,\hat{i}+\sin 30^\circ\, \hat{j}) \\ &=4.38\hat{i}+2.53\hat{j}\quad {\rm nN}\end{align*}
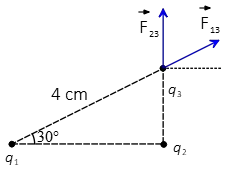
Similarly, the electric force $\vec{F}_{23}$ exerted on charge $q_3$ due to charge $q_2$ is along the $y$ direction and away from charge $q_3$. Its magnitude is also found as \begin{align*} F_{23}&=k\frac{|q_2q_3|}{d_{23}^2}\\ \\ &=\frac{(8.99\times 10^{9})(3\times 10^{-9})^2}{2^2}\\ \\ &=20.2\times 10^{-9}\quad {\rm nC}\end{align*} Therefore, in component form is \[\vec{F}_{23}=20.2\,\hat{j}\quad{\rm nN}\]Vector summing them get the net force on charge $q_3$ as below \begin{align*} \vec{F}_3&=\vec{F}_{13}+\vec{F}_{23}\\ &=4.38\hat{i}+22.53\hat{j}\quad {\rm nN}\end{align*} The magnitude of the net force is determined from its components as below \begin{align*} F_3 &=\sqrt{F_x^{2}+F_y^{2}}\\\\&=\sqrt{(4.38\times 10^{-9})^{2}+(22.53\times 10^{-9})^{2}}\\ \\ &=22.9\times 10^{-9}\quad {\rm N}\end{align*}The net force makes an angle $\theta$ with the $x$ axis whose value is found as below \begin{align*} \theta &=\tan^{-1}\left(\frac{F_y}{F_x}\right)\\ \\ &=\tan^{-1}\left(\frac{22.53}{4.38}\right)\\ \\ &=79^\circ \end{align*} With these electric charge solved problems you can understand more about the properties of the electric charges in physics.
Problem (5): Three point charges are fixed at the corners of a triangle as the figure below. We place another positive charge $q_4=1\,{\rm \mu C}$ in the middle of the line connecting charges $q_2$ and $q_3$. Find the magnitude of the electric force on this extra charge.
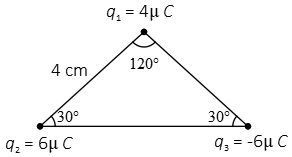
Solution: two facts about this triangle:
Fact (1): If a triangle has two equal angles then it is an isosceles triangle.
Fact (2): The line joining the apex to the base of an isosceles triangle at a right angle, divide the base into two equal parts.
With these notes in mind, using trigonometry we can compute each of these equal parts as below \[BD=AB\cos 30^\circ=4\times \left(\frac{\sqrt{3}}{2}\right)=2\sqrt{3}\]Thus, the charge $q_4$ is placed $2\sqrt{3}\,{\rm cm}$ away from each other charges $q_2$ and $q_3$.
By applying Coulomb's law the magnitude of the electric forces $F_{24}$ (green vector) and $F_{34}$ (Red vector) are found below
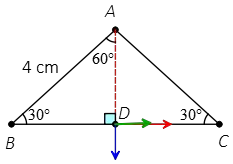
\begin{align*}F_{24}&=k\frac{|q_2q_4|}{d_{24}^2}\\ \\ &=(8.99\times 10^{9})\frac{(1\times 10^{-6})(6\times 10^{-6})}{(2\sqrt{3}\times 10^{-2})^2}\\ \\&=45\quad {\rm N}\end{align*} It is directed away from charge $q_2$ along the line BC in the positive $x$ axis. \[\vec{F}_{24}=45\,{\rm N}\quad \hat{i}\]Since the charge $q_3$ has the same magnitude as charge $q_2$ and is at the same distance so its magnitude is the same as previous \[F_{23}=F_{24}=45\,{\rm N}\]But since it has opposite sign, so it attracts charge $q_4$ to ward the positive $x$ axis.
Similarly, charge $q_1$ repel the charge $q_4$ along the line AD toward the negative $y$ direction (blue vector). Its magnitude is \begin{align*}F_{14}&=k\frac{|q_1q_4|}{d_{14}^2}\\ \\ &=(8.99\times 10^{9})\frac{(4\times 10^{-6})(1\times 10^{-6})}{(0.02)^2}\\ \\&=90\quad {\rm N}\end{align*}Therefore, in vector notation is written as \[\vec{F}_{14}=-90\,{\rm N}\quad \hat{j}\]Vector summing all these force, superposition principle, get the resultant (net) electric force on the charge $q_4$ as below \begin{align*} \vec{F}_4&=\vec{F}_{14}+\vec{F}_{24}+\vec{F}_{34} \\ \\ &=(-90\,\hat{j}+2\times 45\,\hat{i})\\ \\ &=(90)(\hat{i}-\hat{j})\end{align*}The magnitude of the net force is found by taking square root of sum of the squares of its components as below \begin{align*} F_4&=\sqrt{F_x^{2}+F_y^2}\\ \\ &=\sqrt{(90)^{2}+(-90)^{2}}\\ \\&=90\sqrt{2}\end{align*}The direction of the net force with the positive $x$ axis is determined as below formula
\begin{align*} \theta&=\tan^{-1}\left(\frac{F_y}{F_x}\right)\\ \\&=\tan^{-1}\left(\frac{-90}{90}\right)\\ \\&=-45^\circ\end{align*} The minus sign indicates that the force is below $x$ axis and lies in the fourth quadrant.
Problem (6): Two point charges of $q_1=-2\,{\rm \mu C}$ and $q_2=4\,{\rm \mu C}$ are separated by distance $L$ apart. Where should a third point charge be placed so that the electric force on it is zero?
Solution: According to Coulomb's law, the electric force between two point charges is along the line connecting those together. Thus, there is always the third point, between or outside them depending on signs of charges, that the net force on the other point charge becomes zero.
In this problem, first sketch a figure showing the two charges, the $x$ axis. Next, place a third charge (no matter what sign it has!) on an arbitrary point between the charges and draw the electric forces exerted on it due to the other two charges as below

As you can see, the two electric force vectors are in opposite directions.
Therefore, between two charges with opposite signs, we can find a point where those forces exactly balance each other. But at what distance?
Let's consider the charge $q_3$ is placed at a distance $x$ from the smaller charge $-2\,{\rm \mu C}$ and $L-x$ from the other charge.
Using Coulomb's law, find the magnitude of the electric forces on the charge $q_3$, and then equate them together.
\begin{align*} F_{13}&=F_{23}\\ \\ k\frac{|q_1q_3|}{d_{13}^2}&=k\frac{|q_2q_3|}{d_{23}^2}\\ \\ \frac{2}{x^2}&=\frac{4}{(L-x)^2}\\ \\ \pm \frac{1}{x}&=\frac{2}{L-x}\\ \\ \Rightarrow L-x &= \pm 2x \end{align*}In the fourth equality, the square root is taken from both sides. Now, solve the last equality to find the location of the third charge as below
\begin{gather*} L-x=+2x \Rightarrow x=\frac 13 L \\ \\ L-x=-2x \Rightarrow x=-L \end{gather*} The second answer is not acceptable, because it indicates that the third point lies in the left side of the $-2\,{\rm \mu C}$ which is contradicted our initial reasoning that it must be placed at distance $x$ on the right side of $-2\,{\rm \mu C}$.
Practice Problem (7): In the above, solve the problem by considering those charges be $q_1=+2\,{\rm \mu C}$ and $q_2=+4\,{\rm \mu C}$.
Hint: The location of the third point charge must be outside the two above charges. Justify why and at what distance of smaller charge?
Problem (8): Three point charges are placed at the corners of a triangle as shown in the figure below. Find the magnitude and direction of the net electric force on the third charge due to the charges $q_1$ and $q_2$.

Solution: Applying Coulomb's law to find the magnitude of each force. Each force is along the line connecting the two charges involved.
The magnitude of electric force vector $\vec{F}_{13}$ is \begin{align*}F_{13}&=k\frac{|q_1q_3|}{d_{13}^2}\\ \\ &=(9\times 10^9)\frac{(32\times 10^{-6})(25\times 10^{-6})}{(0.25)^2}\\ \\&=115.2\quad {\rm N}\end{align*}
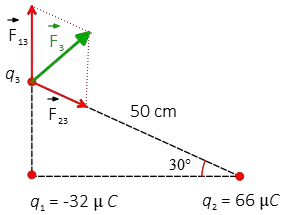
In above, we used the trigonometry to find the distance of charge $q_1$ to charge $q_3$ as below \[d_{13}=50 \sin 30^\circ=25\,{\rm cm}\] Thus, in vector form notation is written as below \[\vec{F}_{13}=115.2\,{\rm N}\, \hat{j}\]Similarly, the magnitude of electric force vector $\vec{F}_{23}$ is \begin{align*}F_{23}&=k\frac{|q_2q_3|}{d_{23}^2}\\ \\ &=(9\times 10^9)\frac{(66\times 10^{-6})(25\times 10^{-6})}{(0.25)^2}\\ \\&=59.4\quad {\rm N}\end{align*} The direction of this force in component form is a bit difficult. To decompose it into its components (pink vectors), note that this force makes an angle of $30^\circ$ with the positive $x$ axis. Therefore, we have \begin{align*} \vec{F}_{23}&=F_{23}\cos 30^\circ\,\hat{i}+F_{23}\sin 30^\circ\,(-\hat{j})\\ &=(59.4\times \frac{\sqrt{3}}2)\hat{i}+(59.4\times \frac 12)(-\hat{j})\\ &=51.5\,\hat{i}-29.7\,\hat{j}\quad {\rm N}\end{align*}
The directions of the forces are shown in the figure:
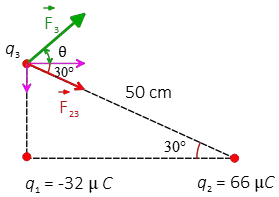
Now, summing vector these forces get the net electric force (dark green vector) on the third charge (Principle of superposition): \begin{align*} \vec{F}_3 &= \vec{F}_{13}+\vec{F}_{23}\\ \\ &=115.2\,\hat{j}+51.5\,\hat{i}-29.7\,\hat{j}\\ \\ &=51.5\,\hat{i}+85.5\,\hat{j}\quad {\rm N}\end{align*} The magnitude of the net force is \[F_3=\sqrt{(51.5)^{2}+(85.5)^{2}}=99.8\,{\rm N}\] and it makes an below angle with the positive $x$ axis \[\theta =\tan^{-1}\left(\frac{85.5}{51.5}\right)=59^\circ\]
Summary:
In this article, several problems about electric forces are solved. All these questions are solvable by Coulomb's law formula. For more practice on forces, you can also check out these ap physics 1 forces problems here.
Author: Dr. Ali Nemati
Date Published: 4/1/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
