AP Physics 1 Forces Practice Problems + Sample MCQs
In this long article, over 30 multiple-choice questions are solved on forces for the AP Physics 1 exam. Each topic is categorized for better practice.
In the pdf version of this article, you can find all these questions along with additional solved problems.
Forces Practice Problems: AP Physics
All forces questions on the AP Physics 1 exams, cover one of the following subsections:
Newton's First law
Problem (1): In the figure below, we first gently pull the thread down and gradually increase this force until one of the threads connected to the hanging block becomes torn. We again repeat this experiment, but this time, the thread is pulled abruptly down so that one of the threads breaks. Which of the following is correct about this experiment?
(a) In both experiments the lower thread breaks.
(b) In both experiments the upper thread breaks.
(c) In the first experiment, the upper thread breaks but in the second the lower thread.
(d) In the first experiment, the lower thread breaks but in the second the upper thread.
Solution: In the first experiment, the force is applied gently to the lower thread, so this thread and the block form a unit object, and we can ignore this lower thread from the analysis. When the force is increased, the upper thread, which bears the block's weight, is torn.
Due to Newton's first law of motion, when the force is applied abruptly to the lower thread, the hanging block at the other end is still at rest and wants to remain in this situation. Consequently, in the second experiment, the lower thread is torn.
Problem (2): Which of the following equations obeys Newton's first law of motion?
(a) $x=2\sqrt{t}$ (b) $x=-10t^2+2t$
(c) $x=10t$ (d) $v=-10t+3$
Solution: Newton's first law of motion states that an object maintains its state of stillness or constant speed until a net force acted on it. As you can see from this statement, the object has to be at rest or moving at a constant speed in order to apply the first law.
All these conditions can be translated into the following kinematics equations:
At rest: $x=0$
Moving at constant speed $v$ : $x=vt$
Therefore, only choice (c) has the form of a motion in which the object moves at a constant speed. Thus, the correct choice is (c).
Problem (3): An automobile moves along a straight road at a constant speed. The friction force between the car's tire and the pavement is $2500-{\rm N}$, and the driving force equals $5500\,{\rm N}$. What air resistive force is applied to the car?
(a) 3000 N (b) 3500 N
(c) 8000 N (d) zero
Solution: Since the car moves at a constant speed, according to Newton's first law no net force is applied to it otherwise, the car accelerates (according to Newton's second law). Therefore, the driving force must be equal to the opposing forces of friction and air resistance. \begin{gather*} F_{air}+F_{friction}=F_{driv} \\\\ F_{air}+2500=5500 \\\\ \Rightarrow \boxed{F_{air}=3000\,{\rm N}}\end{gather*} Hence, the correct choice is (a).
Problem (4): Which of the following is an incorrect phrase about forces in physics?
(a) The forces are the result of the interaction of two objects with each other.
(b) The forces are vector quantities that have a magnitude in addition to the direction.
(c) In modeling the physics problems, sometimes assumes that the forces are applied to the center of the mass of the object.
(d) The only consequence of applying forces to an object is a change in its velocity.
Solution: The correct choice is (d). Because it is possible some forces are applied to an object at rest and the object stays at rest or in another situation, those forces are applied to a constant speed moving object but the object's velocity does not change. This occurs when the resultant of those forces is zero. This is the same as Newton's first law of motion.
All other options are correct definitions of vectors in physics.
Newton's 2nd law
Problem (5): Two forces of $\vec{F}_1=2\hat{i}+6\hat{j}$ and $\vec{F}_2=\hat{i}-2\hat{j}$ are acting to a moving object of mass $2\,{\rm kg}$. What acceleration will the object find in ${\rm \frac ms}$?
(a) $2$ (b) $2.5$
(c) $3$ (d) $3.5$
Solution: According to Newton's second law, a net force applied to an object can accelerate it by $a=\frac{F_{net}}{m}$. In this case, we are given two force vectors. First, find its resultant (net) vector by adding them as below (superposition principle). \begin{align*} \vec{F}_{net}&=\vec{F}_1+\vec{F}_2 \\\\ &=2\hat{i}+6\hat{j}+\hat{i}-2\hat{j} \\\\ &=3\hat{i}+4\hat{j}\end{align*} The magnitude of this net force is found by the Pythagorean theorem \begin{align*} F&=\sqrt{F_x^2+F_y^2}\\\\ &=\sqrt{3^2+4^2}\\\\ &=5\quad{\rm N}\end{align*} Now that the magnitude of the net force applied to the object found, its acceleration is computed as below \[a=\frac{F_{net}}{m}=\frac{5}{2}=2.5\,{\rm m/s^2}\] Hence, the correct answer is (b).
Problem (6): Three forces of $\vec{F}_1=20\hat{i}-50\hat{j}$, $\vec{F}_2=10\hat{i}+20\hat{j}$, and $\vec{F}_3=-10\hat{i}$ are acting on a $5-{\rm kg}$ object simultaneously. What is the magnitude of the acceleration of the object?
(a) $1$ (b) $5$
(c) $10$ (d) $15$
Solution: Another practice problem in vectors in the AP Physics 1 exam. Three force vectors are given and asked for acceleration. Again, find the resultant force vector acted on the object. Summing the corresponding components gives the components of the net force as below \[\vec{F}_{net}=30\hat{i}-40\hat{j}\] The magnitude of this force vector is found as \[F_{net}=\sqrt{30^2+(-40)^2}=50\,{\rm N}\] Dividing the net force by the object's mass gives the acceleration \[a=\frac{F_{net}}{m}=\frac{50}{5}=10\,{\rm m/s^2}\] Hence, the correct answer is (c).
Problem (7): A $500-{\rm g}$ ball is dropped from rest from a height of $25\,{\rm m}$. After striking the ground it rebounds at a height of $15\,{\rm m}$. Assume the contact time between the ball and the surface of the ground is $2\,{\rm ms}$. What average force was applied to the ball in $\rm N$? (take $g=9.8\,{\rm m/s^2}$)
(a) 9820 (b) 1250
(c) 125 (d) 982
Solution: Newton's second law of motion has two mathematical forms; one is $\vec{F}_{net}=m\vec{a}$, and the other is $\vec{F}_{av}=\frac{\Delta \vec{P}}{\Delta t}$. The second form is more suitable to solve the average force exerted to an object experiencing a change in its velocity. The change in the momentum is defined as $\Delta \vec{P}=m(\vec{v}_2-\vec{v}_1)$.
In this problem, the touching time with the ground is given by $\Delta t=2\times 10^-3 \,{\rm s}$. Now, if we find the change in the momentum, then we will be able to determine the average force during the contact.
Initially, the ball is dropped from rest, so its initial velocity is zero. Using the kinematics equation $v^2-v_0^2=2(-g)\Delta y$, we can find the velocity just before hitting the ground. (notice that to use this equation, you must choose a reference point). We take the releasing point as the reference, the ball hit the ground $25\,{\rm m}$ below this point, so we must set $\Delta y=-25\,{\rm m}$ in above. \begin{gather*} v^2-v_0^2=2(-g)\Delta y \\\\ v^2-0=2(-9.8)(-25) \\\\ v_{bef}=\sqrt{490}=-22.14\,{\rm m/s}\end{gather*} The negative indicates that the ball's velocity is down. Now, we must compute the velocity at which the ball rises from the surface and goes up by $15\,{\rm m}$. This time take the ground as a reference, so $\Delta y=+15\,{\rm m}$. At this point, the ball's speed is zero, since the ball rises so high that its velocity becomes zero. \begin{gather*} v^2-v_0^2=2(-g)\Delta y \\\\ 0-v^2=2(-9.8)(15) \\\\ v_{aft}=\sqrt{294}=+17.14\,{\rm m/s}\end{gather*} The positive indicates that the velocity is up. This is the ball's velocity just after rising the surface. The change in the momentum is also found as \begin{align*} \Delta \vec{P}&=m(\vec{v}_{aft}-\vec{v}_{bef}) \\\\ &=(0.5)(17.14-(-22.14)) \\\\ &=19.64\quad {\rm \frac{kg.m^2}{s}}\end{align*} Dividing the change in momentum by the contact time to find the average force applied to the ball \begin{align*} \vec{F}_{av}&=\frac{\Delta \vec{P}}{\Delta t} \\\\ &=\frac{19.64}{2\times 10^-3}\\\\ &=\boxed{9820\quad {\rm N}} \end{align*} Hence, the correct answer is (a).
Problem (8): What average force is needed to stop a $3500\,{\rm kg}$ SUV in $5\,{\rm s}$ if it is traveling at $72\,{\rm km/h}$?
(a) 14000 N (b) 50400 N
(c) 12500 N (d) 15000 N
Solution: Another combination question of kinematics and dynamics in the AP Physics 1 exam. First, we must find the acceleration of the car using the kinematics equation $v=v_0+at$ during this time interval. The final speed is zero, and take the initial speed as $72\,{\rm km/h}$. Convert it to the SI units of velocity as below \[72\,{\rm \frac{km}{h}}=72\,{\rm \left(\frac{1000}{3600}\right)\,\frac ms}=20\,{\rm \frac ms}\] The acceleration is found as below \begin{gather*} v=v_0+at \\\\ 0 = 20+5a \\\\ \Rightarrow \quad a=-4\,{\rm m/s^2}\end{gather*} The negative indicates the direction of the acceleration which is in the opposite direction of the motion. Now, using the formula $F_{net}=ma$, we can find the average force that is required to stop this car as below \[F=3500\times 4=\boxed{14000\,{\rm N}}\] Hence, the correct answer is (a).
Solve more kinematics questions to master this topic.
Newton's third law
Problem (9): In the figure below, an object is hung from a massless thread. Assume $\vec{W}$ is the gravity force vector applied to the mass $m$ by Earth. What is the reaction of the force exerted on the ceiling by the thread and the reaction of the force exerted on the weight by the thread?
(a) $\vec{W}$,$\vec{W}$ (b) $-\vec{W}$,$\vec{W}$
(c) $\vec{W}$,$-\vec{W}$ (d) $-\vec{W}$,$-\vec{W}$
Solution: This is another sample conceptual question about Newton's third law which appears in the AP Physics 1 exam. Break the thread from some desired point. At this point, these two forces, equal in magnitude but opposite in direction, form as shown in the figure below. The upward force is the same well-known tension force in the thread. The downward force is also the force exerted by the thread on the ceiling and pulls it down. The reaction of this force, according to Newton's third law, is toward up or $-\vec{W}$.
On the other hand, the thread pulls the weight up by the tension force $T$. The reaction of this force must be in the opposite direction with the same magnitude. Thus, the reaction force is down or $\vec{W}$. Hence, the correct answer is (b).
Air Resistance force
Problem (10): A rain droplet comes out of a cloud nearly at rest and starts moving down. From the moment of leaving the cloud to reaching the ground, how does the air resistance force change?
(a) continuously increasing.
(b) first increases, then remain constant.
(c) it remains constant.
(d) first increases then decrease.
Solution: In all AP Physics 1 exam problems, keep in mind that the air resistance is proportional to the falling velocity of the object through the air, $f\propto v$. When the rain droplet detached from the cloud, due to gravity its speed will increase. Thus, the air resistance also increases uniformly. This increase in air resistance lasts until it is balanced with the object's weight. From that moment on, the object's acceleration becomes zero and its speed remains unchanged. Hence, the correct answer is (b).
Problem (11): Which of the following velocity vs. time graphs below has a correct description for the rain droplet of the previous problem?
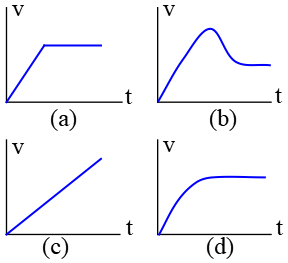
Solution: The correct answer is (d). Refer to the pdf version to find the explanation.
Problem (12): A $400-{\rm g}$ object releases from a nearly high height. Assume a constant resistance force of $1.2\,{\rm N}$ is exerted on it during falling. What acceleration will the object experience in $m/s^2$?
(a) $7$ (b) $1.3$
(c) $-7$ (d) $-1.3$
Solution: Upon releasing the object, it falls down and its speed is increasing. Take the direction of acceleration, which is down along the gravity force, as positive. To a falling object two forces are acting; downward weight, and upward air resistive force $f_R$. The resultant of these two forces accelerates the object down. Now, write Newton's second law and solve for $a$ \begin{align*} F_{net}&=ma \\\\ mg-f_R &=ma \\\\ (0.4)(10)-1.2 &=(0.4)a \\\\ \Rightarrow \quad a&=7\,{\rm m/s^2}\end{align*} Hence, the correct answer is (a).
Problem (13): An apple is thrown into the air vertically upward and some later time it falls down and reaches the same original level. Which of the following is a correct phrase?
(a) Acceleration during ascending and descending are equal.
(b) Acceleration during ascending is higher than descending.
(c) The time of ascending and descending are the same.
(d) The time of ascending is higher than descending.
Solution: The ball is thrown into the air, so we cannot ignore the air resistance. When the ball is going up, this resistive force is $f$ down and when it is going down, the resistive force is up. Take up as positive. Apply Newton's second law of motion to these situations and solve for the accelerations. For moving up: \[-mg-f=ma_U \] For going down: \[f-mg=ma_D\] As you can see, the magnitude of acceleration for ascending is higher than descending. \[|a_U|>|a_D|\] Hence, the correct answer is (b).
Normal force
Problem (14): A 2-kg crate is pulled over a rough horizontal surface by the force of $25\,{\rm N}$ which makes an angle of $37^\circ$ with the horizontal. Assume the coefficient of friction is $0.2$. Find the normal force applied to the crate by the surface.
Solution: First, draw a free-body diagram and label all forces acting on the crate as shown below. We know that the object does not move vertically, so its acceleration in this direction must be zero, $a_y=0$. The external force $F_P$ is applied at an angle, so resolve it into its components over $x$ and $y$ axes. \begin{gather*} F_{Px}=F_P \cos 37^\circ \\\\ F_{Py}=F_P\sin 37^\circ \end{gather*} Apply Newton's second law to the forces along the vertical direction and solve for $F_N$ as below \begin{align*} \Sigma F_y&=ma_y\\\\ F_N+ F_{Py}-mg&=0 \\\\ \Rightarrow F_N&=mg-F_P \sin 37^\circ \\\\ &=(2\times 10)-25 (0.6) \\\\ &=\boxed{5\,{\rm N}}\end{align*}
Problem (15): Two boxes are on top of each other as shown in the figure below. The lower weight is $m_1=15\,{\rm kg}$ and the upper weight is $m_2=5\,{\rm kg}$. What is the normal force that the surface exerts on $m_1$ and the normal force that $m_1$ exerts on $m_2$, respectively in $N$?
(a) 50 , 150 (b) 150 , 50
(c) 200 , 50 (c) 100 , 50
Solution: The following figures show a free-body diagram in which all forces acting on the masses $m_1$ and $m_2$ are depicted.
$N_{S}$ is the normal force exerted by the surface on $m_1$. Similarly, $N_{12}$ is the normal force exerted by $m_1$ on $m_2$. According to Newton's third law, the force that both masses exerted on each other is the same in magnitude but opposite in direction. Thus, the $\vec{N}_{12}=-\vec{N}_{21}$. The masses are at rest, so the net force acting on each object is zero. Balancing the forces exerted on $m_2$ first, gives us \begin{align*} N_{12}-m_2g&=0 \\ N_{12}&=m_2g\\ &=5\times 10 \\&=\boxed{50\,{\rm N}}\end{align*} Thus, the normal force exerted on $m_2$ by the bottom box of $m_1$ is $50\,{\rm N}$. Correspondingly, the force that the mass $m_2$ exerts on $m_1$ has the same magnitude but in the opposite direction which is down. Apply Newton's law of motion again for $m_1$, we will have \begin{align*} N_{S}-N_{21}-m_1g&=0 \\ \Rightarrow N_{S}&=N_{21}+m_1g \\ &=50+(15\times 10) \\ &=\boxed{200\,{\rm N}}\end{align*} Hence, the correct answer is (c).
Practice Problem (16): In the following figure, What are the normal forces at the surfaces of $A$, $B$, and $C$ in $\rm N$, respectively?
(a) 200, 120, 50 (b) 80, 70, 50
(c) 200, 70, 60 (d) 120, 200, 80
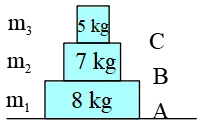
Solution: The correct answer is (a). Refer to the pdf version for the explanation.
Practice Problem (17): Two blocks of masses $m_1=20\,{\rm kg}$ and $m_2=10\,{\rm kg}$ are in an elevator. The elevator moves up at an increasing rate of $2\,{\rm m/s^2}$. How many times is the force that $m_1$ exerts on $m_2$ than the force exerted on the surface by $m_1$?
(a) $\frac 12$ (b) $2$
(c) $\frac 13$ (d) $3$
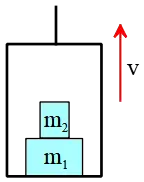
Solution: the correct answer is (c).
Problem (18): A $2-{\rm kg}$ box is held fixed against a rough wall as the figure is shown below. What minimum force will require to keep the box from sliding down? Assume $\mu_s=0.4$ and $g=10\,{\rm m/s^2}$.
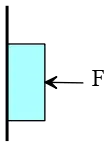
Solution: Draw a free-body diagram and label each force on it. You push the box against the wall with a force of $F$ rightward. The wall also exerts a normal force on the box in the opposite direction of $F$. Vertically exerted forces are; downward weight $W=mg$, and the upward static friction force $f_s$.
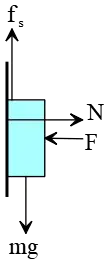
The box is held fixed at the wall, so the net force on it is zero. Balancing the forces along the $x$ axis gives us the normal force exerted on the box by the wall \[N=F\] The box is to be at rest, so the box's weight must be balanced with the maximum static friction force. Thus, \[f_{s,max}=mg\] On the other hand, recall that $f_{s,max}=\mu_s N$. By combining these three equations, we obtain \begin{gather*} f_{s,max}=\mu_s N \\\\ mg=\mu_s F \\\\ \Rightarrow F=\frac{mg}{\mu_s}\end{gather*} Substituting the values into above, we obtain the required force to hold the box fixed at the wall. \[F=\frac{2\times 10}{0.4}=50\,{\rm N}\]
Tension force
Problem (19): A block of mass $m=10\,{\rm kg}$ is hung from two identical strings which makes an angle of $37^\circ$ with the vertical. What is the tension in each of the strings? (Assume $\cos 37^\circ=0.8$)
(a) 500 N (b) 3000 N
(c) 375 N (d) 400 N
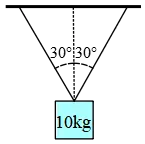
Solution: Draw a free-body diagram as below and label each force. The cords are identical so the tension force in each is the same. Resolving it into its components gives us \begin{gather*} T_x=T\sin \theta \\ T_y=T\cos\theta \end{gather*} As you can see, two identical tension forces upward, and weight force downward, are applied to the object. In the horizontal direction, there are only two identical components of tension, but in opposite directions. Thus, these components cancel out each other.
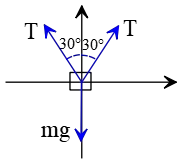
In the vertical direction, the $y$-component of tension forces balances the object's weight. Therefore, we have \begin{align*} 2T\cos\theta&=mg \\\\ \Rightarrow T&=\frac{mg}{2\cos\theta}\\\\&=\frac{60\times 10}{2\cos 37^\circ}\\\\&=\boxed{375\quad{\rm N}}\end{align*} Hence, the correct answer is (c).
Problem (20): In the following figure, what is the tension in the inclined and horizontal cords supporting a weight of $60\,{\rm kg}$, respectively? (Take $\sin 37^\circ=0.6$ and $\cos 37^\circ=0.8$)
(a) 1000 N , 800 N (b) 800 N , 1000 N
(c) 1333 N , 450 N (d) 800 N , 2000 N
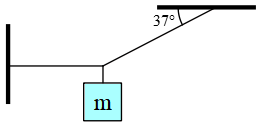
Solution: The object is at rest without any movement, so it is in equilibrium. According to Newton's second law, the equilibrium condition is the net force on the object must be zero. Three forces are acting on the object as shown in the free-body diagram below.
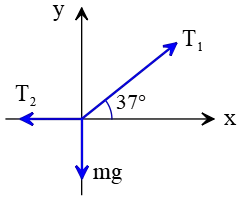
We are assumed that the tension in the inclined cord is $T_1$ and in the horizontal cord is $T_2$. Resolve the inclined tension $T_1$ into $x$ and $y$ components. Balancing the forces along the vertical and horizontal directions gives us \begin{gather} T_1 \sin 37^\circ=mg \\ T_1 \cos 37^\circ=T_2 \end{gather} Dividing the first expression by the second, the tension $T_1$ cancels out, and we have left the tension $T_2$ as below \begin{align*} T_2&=\frac{mg}{\tan 37^\circ} \\\\ &=\frac{600}{0.6/0.8}\\\\&=\boxed{800\quad {\rm N}}\end{align*} where we used the relation below \[\tan 37^\circ=\frac{\sin 37^\circ}{\cos 37^\circ}\] Substitute $T_2=800\,{\rm N}$ into the second equation $(2)$ and solve for $T_1$ as below \begin{align*} T_1&=\frac{T_2}{\cos 37^\circ}\\\\ &=\frac{800}{0.8}\\\\&=\boxed{1000\quad {\rm N}} \end{align*} Hence, the correct answer is (a).
Problem (21): From a cable, it is used to accelerate a $200-{\rm kg}$ body vertically upward at a constant rate of $2\,{\rm m/s^2}$. What is the maximum tension in the cable in ${\rm N}$? (Take $g=10\,{\rm m/s^2}$).
(a) 1600 (b) 2000
(c) 1200 (d) 2400
Solution: Take the direction of the motion to be the positive direction. Two forces; upward tension, and downward weight are acting on the body. The net force of these two gives an upward acceleration to the object. Applying Newton's second law and solving for the tension in the cable get \begin{align*} T-mg&=ma \\ T&=m(g+a) \\ &=200(10+2) \\&=\boxed{2400\quad \rm N} \end{align*} Hence, the correct answer is (d).
Problem (22): A rope is stretched between two poles $10\,{\rm m}$ apart. A $1-\rm {kg}$ bird sits on the midpoint of the rope so that sag of $12^\circ$ is formed. What is the tension in the rope at this point in $\rm N$?
(a) 25 (b) 30
(c) 20 (d) 40
Solution: Draw a free-body diagram, and specify all forces acting on that point. To that point three forces are applied; the bird's weight downward and two equal tensions toward the left and right of that point. Since the rope is not moving up or down and is at rest, its acceleration is zero.
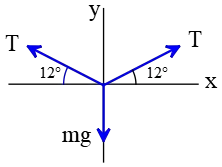
Balancing the forces at that point along the vertical gives us \begin{gather*} T \sin 12^\circ+T\sin 12^\circ-mg =0 \\\\ 2T\sin 12^\circ=mg \\\\ \Rightarrow \quad T=\frac{mg}{2\sin 12^\circ}\end{gather*} Substituting the numerical values into it, we will obtain the tension in the rope as below \[T=\frac{1\times 10}{2\times 0.2}=25\,{\rm N}\]
Weight force
Problem (23): In the following figure, what is the direction of the gravitational force acting on person A and B, respectively?
(a) $\searrow$ , $\swarrow$ (b) $\downarrow$ , $\nearrow$
(c) $\nwarrow$ , $\nearrow$ (d) $\downarrow$ , $\downarrow$
Solution: The direction of the gravitational force acting on any object is always toward the center of Earth. Thus, the correct answer is (a).
Problem (24): The weight of an object on the surface of Mars equals $9\,{\rm N}$. What is the mass of the object and its weight on the surface of the Moon in SI units? (Consider the gravitational acceleration on the surface of Mars and the Moon $3.6\,{\rm m/s^2}$ and $1.6\,{\rm m/s^2}$, respectively).
(a) 0.9 , 1.44 (b) 0.9 , 4
(c) 2.5 , 1.44 (d) 2.5 , 4
Solution: The weight of an object is defined as $W=mg$ where $g$ is the acceleration of gravity on the surface of a planet. The weight on Mars is given, so we can find the mass of the object \[m=\frac{W_{Mars}}{g_{Mars}}=\frac{9}{3.6}=2.5\,{\rm kg}\] Notice that the mass of any object is constant everywhere, regardless of where it is located.
Now that the mass is known, use the weight formula to find the object's weight on the Moon \begin{align*} W_{Moon}&=mg_{Moon} \\\\ &=2.5\times 1.6 \\\\ &=\boxed{4\,\rm N}\end{align*} Note that the SI units of mass and weight are $\rm kg$ and $\rm N$, respectively. Hence, the correct answer is (d).
Elevators
Problem (25): An object weighing $400\,{\rm g}$ is on a spring scale inside an elevator. If the elevator is moving down and slowing at a constant rate of $2\,{\rm m/s^2}$, what is the reading of the scale?
(a) 4.8 N (b) 3.2 N
(c) 4 N (d) 3.8 N
Solution: First of all, draw a free-body diagram and show all forces acting on the object inside the elevator. Two forces are acting on the object; the weight force downward $W$, and the normal force $F_N$ by the scale on the object. This normal force is the same reading of the scale.
For simplicity, in all the AP physics force problems, take the acceleration direction as the positive and in accordance with it write down Newton's second law of motion.
Recall that whenever we have $av>0$, then the motion is slowing down. In this case, the elevator moving down and slowing. We conclude that the acceleration must be in the opposite direction of the velocity, which is down. Thus, the acceleration of the elevator is upward.
According to the free-body diagram and Newton's law, we have \begin{gather*} F_{net}=ma \\\\ N-mg=ma\\\\ N=m(g+a) \end{gather*} Substituting the numerical values into it, we have \[N=0.400(10+2)=4.8\,{\rm N}\] Keep in mind that the number that the scale shows is the same force applied by the scale on the object.
Hence, the correct answer is (a).
Problem (26): A person weighing $60,{\rm kg}$ stands on a scale in a moving elevator. The elevator starts moving down initially at rest. The velocity vs. time graph for this motion is shown below. What is the ratio of the scale reading at the instant $t_1=4\,{\rm s}$ to the apparent weight of the person at time $t_2=15\,{\rm s}$?
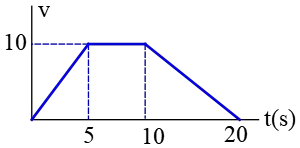
Solution: Refer to the pdf version for the explanation.
Inclines
In this section, some problems about inclined planes that appear in the AP Physics 1 exams are presented.
Problem (27): A box of mass $m=7\,{\rm kg}$ lie on top of a frictionless incline plane of angle $20^\circ$. What acceleration (in ${\rm m/s^2}$) does the block find as it slides down the incline? (take $g=10\,{\rm m/s^2}$.
(a) 3.4 (b) 0.34
(c) 2.4 (d) 10
Solution: The incline has a smooth surface, so there is no friction. The only force along the incline is the component of the weight downward, $mg\sin\theta$. This is the force that is responsible for pulling the box down and accelerating it. Applying Newton's second law, $F_{net}=ma$, we have \begin{gather*} F_{net}=ma \\\\ mg\sin\theta=ma \\\\ \Rightarrow \boxed{a=g\sin\theta}\end{gather*} Substituting the numerical values into it, we have \[a=(10) \sin 20^\circ=3.4\,{\rm m/s^2}\] Hence, the correct answer is (a).
Problem (28): A block is kicked up the $22^\circ$ smooth incline plane with an initial speed of $4.5\,{\rm m/s}$.
(a) How far up the incline will it go?
(b) How much time does it take for the block to return to its starting point?
Solution: In this AP force sample question, you must do some calculations on kinematics. "How far" and "How much time" are the frequent phrases use in all the AP physics kinematics problems.
As you know, acceleration is one of the most important kinematic variables. In this case, we must first find it.
(a) The incline is smooth, so the friction is zero. In addition, there is no driving force in this case. Thus, the only force that is exerted on the block is $W_x=mg\sin\theta$ down the incline. Take the direction of motion as positive, so the weight component parallel to the incline $W_x$ is toward the negative direction. Applying Newton's 2nd law, we have \begin{gather*} -mg\sin\theta=ma \\ \Rightarrow \quad a=-g\sin\theta \end{gather*} As you can see, the acceleration is independent of the mass of the object. Substituting the values into the above, we will have \[a=-10\times \sin 22^\circ=3.75\,{\rm m/s^2}\] The negative indicates that the acceleration is toward down the incline. Now that the block's acceleration and initial velocity down the incline are known, we can use the time-independent kinematics equation $v^2-v_0^2=2a\Delta x$, where $\Delta x$ is the displacement over which the block is displaced. Here, we set the final velocity zero, $v=0$, since we want the maximum distance the block moves up. Therefore, \begin{gather*} v^2-v_0^2=2a\Delta x \\\\ 0-(4.5)^2 =2(-3.75) \Delta x \\\\ \Rightarrow \quad \boxed{\Delta x=2.7 \quad {\rm m}}\end{gather*}
(b) In this part, the time it takes for the block to reach the starting point has been wanted. When an object reaches the starting point, then according to the definition of displacement, its displacement is zero, $\Delta x=0$. Thus, in this case, it is better to use the following kinematics equation. \[\Delta x=\frac 12 at^2+v_0t\] Substituting the values into it and solving for $t$, we have \begin{gather*} \Delta x=\frac 12 at^2+v_0t \\\\ 0=\frac 12 (-3.75)t^2+ 4.5t \\\\ 0=t(-3.75t+9) \\\\ \Rightarrow \, t_1=0 \, , \, t_2=2.4\,{\rm s}\end{gather*} In the third line, we factored out $t$. The first solution is for the initial time when the block is kicked up the incline and the second time $t_2$ corresponds to the point when the block has returned to starting position.
Problem (29): Two masses of $m_1=2\,{\rm kg}$ and $m_2=5\,{\rm kg}$ are connected together by a massless rope as shown below. The inclines have a coefficient of kinetic friction of $0.3$. Assume $m_A$ moves down and $m_A$ moves up. The acceleration of this system is closest to (in $m/s^2$).
(a) 0.03 (b) 4.6
(c) 1.4 (d) 3.9
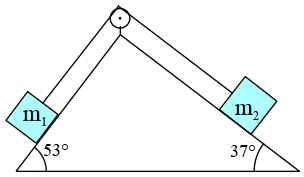
Solution: Two types of external forces are applied to the objects. One is the ubiquitous (on inclines) weight component $W_x=mg\sin\theta$ along the incline and the other is friction force. Take the direction of motion to be positive. Thus, the frictions are in the negative direction. In a free-body diagram, draw and label each force.
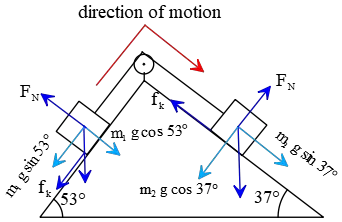
Applying Newton's second law, we have \[ W_{2x}-W_{1x}-f_{k1}-f_{k2}=(m_1+m_2)a\] where $f_k$'s are the kinetic frictions and are defined as $f_k=\mu_k F_N$. The normal force is also found by $F_N=mg\cos\theta$. Combining all these and substituting the numerical values, the frictions and parallel incline weight components are determined as \begin{align*} f_{k1}&=\mu_k m_1g\sin\theta_1\\ &=(0.3)(2)(10) \sin 53^\circ\\&=4.8\,{\rm N} \\\\ f_{k2}&=\mu_k m_2g\sin\theta_2\\ &=(0.3)(5)(10) \sin 37^\circ\\&=9\,{\rm N} \\\\ W_{1x}&=m_1g\sin\theta_1\\ &=(2)(10) \sin 53^\circ \\&=16\,{\rm N} \\\\ W_{2x}&=m_2g\sin\theta_2\\ &=(5)(10) \sin 37^\circ \\&=30\,{\rm N} \end{align*} Now, put these values into Newton's 2nd law written above, \begin{gather*} W_{2x}-W_{1x}-f_{k1}-f_{k2}=(m_1+m_2)a \\\\ 30-16-4.8-9=(2+5)a \\\\ \Rightarrow \quad a=0.028 \quad {\rm m/s^2}\end{gather*} Thus, the acceleration is closest to (a). Hence, the correct answer is (a).
Problem (30): A $3-{\rm kg}$ box has been held fixed on a $30^\circ$ incline by an external force,$F$, perpendicular to it. The coefficient of static friction between the box and the slope surface is $0.3$. What minimum force is required to prevent the box from sliding along the incline?
(a) 76 N (b) 72 N
(c) 24 N (d) 50 N
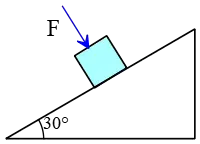
Solution: To the box, the following forces are applied. $mg\sin\theta$ down the incline, the normal force $N$, $mg\cos\theta$, and external force $F$ perpendicular to the incline, and finally the static friction force which is the direction must be determined.
If the external force $F$ is less than a certain value, then the box starts to slide down the incline. Until the box is at rest, the net force along the incline must be balanced with the static friction. \[mg\sin\theta=f_{s,max}=\mu_s N\] On the other hand, the net force along the direction perpendicular to the incline is determined as \begin{gather*} N-mg\cos\theta-F=0\\ \Rightarrow N=mg\cos\theta+F\end{gather*} By combining these two equations and solving for the unknown force $F$, we will have \begin{gather*} mg\sin\theta =\mu_s (mg\cos\theta+F) \\\\ \Rightarrow F=\frac{mg(\sin\theta-\mu_s \cos\theta)}{\mu_s}\end{gather*} where we factored out the common factor $mg$. Substituting the numerical values into it, we obtain the minimum force value for which the block is on the verge of motion. \begin{align*} F&=\frac{mg(\sin\theta-\mu_s \cos\theta)}{\mu_s} \\\\ &=\frac{(3)(10)(\sin 30^\circ-(0.3)\cos 30^\circ)}{0.3}\\\\&=24\quad {\rm N}\end{align*} Hence, the correct answer is (c).
Author: Dr. Ali Nemati
Published: 12/8/2020
© 2015 All rights reserved. by Physexams.com