Potential Energy Problems & Solutions for high schools
Some simple problems about potential energy involving gravitational and spring potential are provided and solved. All of these questions are for high school students.
Potential Energy: Introduction
Potential energy is the energy that an object will have by virtue of its position relative to a reference point. Potential because it has the potential to do work when it is released from that position.
Gravitational Potential Energy Problems
Problem: A rock with a mass of 2 kg is dropped from a height of 10 meters. Calculate the gravitational potential energy of the rock just before it hits the ground.
Solution: The gravitational potential energy due to Earth's gravity is defined as the product of an object's weight $mg$ and its height $y$ above some reference level (such as the ground). \begin{align*} \text{PE}_g &=mgh \\ &=2\times 9.8 \times 10 \\ &= 196\,\rm J \end{align*} Therefore, the gravitational potential energy of the rock just before it hits the ground is 196 Joules.
Problem: A block of mass 2 kg is placed on an inclined plane with an angle of inclination of 30 degrees. Calculate the gravitational potential energy of the block when it is at a height of 5 meters above the ground.
Solution: As defined, the gravitational potential energy possessed by an object located near the Earth's surface is the object's weight $mg$ times its vertical position $h$ above the surface level, $\text{PE}_g=mgh$.
It does not matter how this object was elevated to that height. It might have been lifted by force $F$ directly straight up, pushed with force $F'$ up an incline of length $L$, or lifted with force $F$ up over a stair.
At a height of $h$ above the ground on the inclined plane, the object has the potential energy of $mgh$.
Plugging in the given values into this equation, we get: \begin{align*} \text{PE}_g &=mg\times h\times \sin\theta \\\\ &=(2\times 9.8)(5) \times \sin 30^\circ \\\\ &=49\,\rm J\end{align*}
Problem: When a block is pushed up an incline, how does its potential energy compare to being raised vertically to the same height?
Solution: We must do work to raise an object against Earth's gravity. Gravitational potential energy is defined as the amount of work done against gravity in lifting an object upward times the height $h$ through which this work is applied.
On the other hand, work is defined as the required force $F$ to move an object times the distance it is moved $d$ (in this case, vertically). \[\text{work}=\text{force}\times \text{distance}\] When it comes to gravitational potential energy, the upward force is the weight of the object, $mg$.
Consider a scenario, in which you are going to lift an object straight up to a height of $h$. The amount of work you do to overcome Earth's gravity is equal to the object's weight, $mg$, multiplied by the height $h$ relative to the ground or the floor of a building.
In this case, the amount of gravitational potential energy possessed by the object is given by \[\text{PE}_g=mgh\] In the second scenario, imagine that the object needs to be pushed up an incline of length $L$. From problems involving inclined planes, you have learned that the force required to push a block up a frictionless incline is given by $F=mg\sin\theta$.
Now, when a block is pushed up an incline instead of being lifted vertically, it requires less force, $mg\sin\theta$, compared to lifting it straight up, $mg$. This less force is exerted on the object over a longer distance $L$, along the incline (although, it reaches the same height), compared to exerting a force of $mg$ over height $h$.
From these observations, we can conclude that the work done in pushing the object up the incline is equal to the work done in lifting it straight up to the same height $h$. \[W_{incline}=W_{straight}\] Because, in both scenarios, the object is elevated to the same height, the gravitational potential in both cases is equal. \[\text{PE}_{g-incline}=\text{PE}_{g-straight}\]
Problem: An object weighing 100 N slides down a frictionless ramp inclined at an angle of 40 degrees from the horizontal plane. If its initial height above the ground is measured at 6 meters, calculate its final gravitational potential energy when it reaches the bottom of the ramp.
Solution: What matters for calculating the gravitational potential energy is the position of that object relative to a reference point. Considering the reference point to be at the Earth's surface, the object is initially at height $6\,\rm m$ above the surface. Thus, its potential energy is found to be \begin{align*} \text{PE}_g&=mgh \\ &=100\times 6 \\ &=600\,\rm J\end{align*} Thus, the object initially has 600 joules of potential energy, and when it reaches the bottom of the plane, its position relative to the surface becomes zero, $y_f=0$. As a result, its final potential energy is zero.
Problem A crate weighing 145 N is pushed on an inclined plane with an angle of inclination of 25 degrees for 2 meters. Calculate its gravitational potential energy.
Solution: We are not given the height of the incline or the amount of height by which the crate is vertically displaced. The only given values are the distance traveled over the incline $L$ and its angle $\theta$.
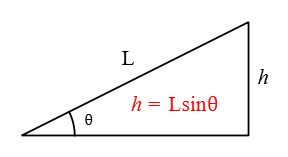
When an object is pushed a distance of $L$ over an incline (wedge, ramp, etc.) angled at $\theta$ to a final height of $h$ above the surface, its potential energy is calculated as $\text{PE}_g=mg\times \underbrace{L \times \sin\theta}_{h}$.
Actually, trigonometry gives us the height $h$ at which the crate is elevated relative to the ground on the incline. \begin{align*} \text{PE}_g &=mg\times\underbrace{L\sin\theta}_{h} \\\\ &= 145\times (2\sin 25^\circ) \\\\ &=122.5\,\rm J\end{align*} In fact, the crate has been elevated a distance of about $h=L\sin\theta=84\,\rm cm$ above the ground.
Problem: On a single day, a mountain climber weighing 75 kg successfully scales a vertical cliff, starting from an elevation of 1500 m and reaching the summit at 2400 m. The following day, she descends from the summit to the cliff's base, situated at an elevation of 1350 m. What is the alteration in her gravitational potential energy during (a) the initial day and (b) the subsequent day?
Solution: To solve any potential energy problem, first consider a reference level as the origin and calculate the position of the object relative to it.
The change in the gravitational potential energy is given by $\rm \Delta PE_g=mg\Delta h$, where $\Delta h$ is the change in the elevation of the object while going up or down.
(a) Assuming the Earth's surface as the origin, The climber's initial and final positions are $y_i=1500\,\rm m$ and $y_f=2400\,\rm m$. The change in the potential energy of the climber during the ascending time interval is \begin{align*} \rm \Delta PE_g&=mg\underbrace{(y_f-y_i)}_{\Delta h} \\\\ &=75\times 9.8\times (2400-1500) \\\\ &=661500\,\rm J\end{align*} Therefore, during the initial day, there is an alteration of 661,500 Joules in her gravitational potential energy.
(b) On the subsequent day, the climber descends from the summit at an elevation of $y_i=2400\,\rm m$ to the cliff's base at an elevation of $y_f=1350\,\rm m$. The change in its height is \[\Delta h=y_f-y_i=1350-2400=-1050\,\rm m\] Notice that since the climber is moving down, $\Delta h$ will be negative. Therefore, the change in its potential energy is \begin{align*} \rm \Delta PE_g&=mg\Delta h \\\\ &=75\times 9.8\times (-1050) \\\\ &=-764250\,\rm J\end{align*} Therefore, during the subsequent day, there is an alteration of -764,250 Joules (or -764.25 kJ) in her gravitational potential energy. The negative sign indicates a decrease in potential energy as she descends.
The two next potential problems are a bit challenging:
Problem: A pocket, weighing 1.25 kg, is raised by a person who is 1.75 m tall to a height of 2.20 m above the ground. Determine the potential energy of the pocket with respect to (a) the ground and (b) the top of the person's head. Additionally, explain how the work performed by the person is connected to the solutions in parts (a) and (b).
Solution: Remember that to find the potential energy of an object, we need a reference point to determine the position of the object relative to that point. The aim of this question is to illustrate the importance of choosing a reference level when solving potential problems.
(a) In this part, we are asked to place the origin on the ground. Hence, the pocket is positioned at a height of $h=2.2\,\rm m$ from the ground, and its corresponding gravitational potential energy is weight times the vertically displaced position \begin{align*} \text{PE}_g &=mgh \\ &=1.25\times 9.8\times 2.2 \\ &=26.96\,\rm J\end{align*}
(b) Now, place the origin of the potential energy at the top of the person's head. In this situation, the pocket $2.2\,\rm m$ above the surface, rests at a height of $\Delta h=2.2-1.7=0.5\,\rm m$ from the person's head. Thus, the potential energy stored in the pocket relative to the person's head will be \begin{align*} \text{PE}_g &=mgh \\ &=1.25\times 9.8\times 0.5 \\ &=6.125\,\rm J\end{align*} The work done by the person $W_{ext}$ to lift the pocket is the change in its gravitational potential energy over the course of which the person applies the force \[W_{ext}=\Delta \text{PE}_g\] The person exerted a force to lift the pocket straight up a distance of $2.2\,\rm m$ from the ground. Therefore, in lifting this pocket to the final height of 2.2 meters, the person does $26.96\,\rm J$ work.
The second part would not make sense. Since the total work done by an external agent (person) over a vertical distance depends on the initial and final heights, which in this case are the ground and 2.2 m height.
Spring Potential Energy
A compressed or stretched spring can do (physical) work on the object attached to it by displacing it. Because of this ability, potential energy can be associated with the spring force, which is called spring or elastic potential energy.
The amount of spring potential energy is directly proportional to the square of the distance $x$ the spring is stretched or compressed from equilibrium. \[\text{PE}_s=\frac 12 kx^2\] where $K$ is the spring constant.
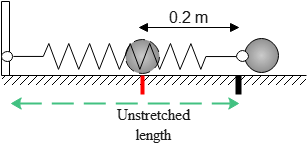
Problem: A spring with a spring constant of 100 N/m is compressed by a distance of 0.2 meters. Calculate the elastic potential energy stored in the spring.
Solution: The given values are $k=100\,\rm N/$ and the amount of compression of the spring from equilibrium (or unstretched length) $x=0.2\,\rm m$. Plugging in the given numerical values into this, we get \begin{align*} \text{PE}_s &=\frac 12 kx^2 \\\\ &=\frac 12 \times 100 \times (0.2)^2 \\\\ &=2\,\rm J\end{align*} Therefore, the elastic potential energy stored in the spring is $2\,\rm N\cdot m$ or 2 joules.
Problem: A rubber band has a spring constant of 50 N/m and is stretched by a distance of 0.1 meters. Calculate the elastic potential energy stored in the rubber band.
Solution: The rubber band acts like a spring since when it is stretched or compressed, it has the ability or potential to work on a body attached to it. Similar to spring, the potential energy stored in the rubber band is determined by $\text{PE}_s=\frac 12 kx^2$, where $x$ is the amount of distance that the band is displaced from its unstretched length.
Plugging in the numerical values into this equation, we get \begin{align*} \text{PE}_s&=\frac 12 kx^2 \\\\ &=\frac 12 \times 50 \times (0.1)^2 \\\\ &=0.25\,\rm J \end{align*}
There is another article that goes into the problems on spring potential energy in detail.
Problem: A bowstring has a spring constant of 200 N/m and is pulled back by a distance of 0.3 meters to shoot an arrow. Calculate the elastic potential energy stored in the bowstring just before releasing it.
Solution: When a bow is stretched, energy is stored in it. Then, this stored energy can do work on an arrow by shooting it. The amount of potential energy stored in the bow is determined as follows \begin{align*} \text{PE}_s&=\frac 12 kx^2 \\\\ &=\frac 12 \times 200 \times 0.3 \\\\ &=30\,\rm J\end{align*}
Conservation of Energy
Problem: A roller coaster starts at the top of a hill with an initial potential energy of 5000 J. As it descends, it encounters friction and air resistance, causing its mechanical energy to decrease. Calculate the final kinetic energy of the roller coaster when it reaches the bottom of the hill.
Solution: To solve this problem, we need to consider the conservation of mechanical energy. The total mechanical energy of the roller coaster is the sum of its potential energy (PE) and kinetic energy (KE). According to the law of conservation of mechanical energy, the total mechanical energy remains constant as long as no external forces are acting on the system.
In this question, we were told that the only forces acting on the roller coaster are friction and air resistance, which are internal forces. Thus, according to the definition of conservation of mechanical energy, these forces cannot change the system's mechanical energy.
Given that the initial potential energy (PE) is $5000\,\rm J$, we can assume that at the top of the hill, all of this potential energy is converted into kinetic energy (KE) when it reaches the bottom.
Therefore, at the bottom of the hill, all $5000\,\rm J$ of potential energy will be converted into kinetic energy. Hence, the final kinetic energy (KE) when it reaches the bottom is $5000\,\rm J$.
Author: Dr. Ali Nemati
Published: Aug 12, 2023
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
