Hooke's law Practice Problems with Solution for High Schools
Get ready to explore Hooke’s Law with our easy-to-understand guide. This article is packed with step-by-step solutions, making your homework a breeze and helping you ace the AP Physics 1 exam.
Hooke's Law Problems:
Problem (1): A block of mass $2\,\rm kg$ is attached to the end of a horizontal spring with spring stiffness constant $k=3\,\rm N/m$. If it is stretched by $10\,\rm cm$, what is the force of the spring?
Solution: According to Hooke’s law, the force exerted by a spring (either stretched or compressed) on an object attached to it is experimentally determined by the following formula: \[F=-kx\] where $k$ is the spring (stiffness) constant whose SI units is $\rm N/m$, and $x$ is the amount of object's displacement from the unstretched position.
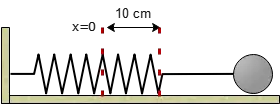
Therefore, the magnitude of the force that is applied to the object is known to be \begin{align*} F&=kx \\ &=3\times 0.10 \\ &=0.3\,\rm N \end{align*} Note that the minus sign in Hooke's law indicates that the force exerted by the spring on the object is in the opposite direction of spring's displacement. Usually, for simplicity, the negative is removed from the calculation, when considering the magnitude of the force.
Problem (2): A mass of $4\,\rm kg$ is placed on top of a vertical string whose base is fixed to the ground. The spring compresses by $2\,\rm cm$.
(a) How much is the spring constant?
(b) How much energy is stored in the spring?
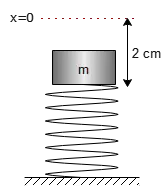
Solution: Here, the spring is placed vertically. In all Hooke's law problems, when an object of mass $m$ rests on a vertical spring whose constant is $k$, then according to Newton's 2nd law, we have \[kx=mg \Rightarrow k=\frac{mg}{x} \]
(a) Applying the above formula, we have \begin{align*} k&=\frac{mg}{x} \\\\ &=\frac{4\times 10}{0.02} \\\\ &=\boxed{2000\,\rm N/m} \end{align*}
(b) The spring potential energy is calculated by the following formula \[PE_s=\frac 12 kx^2\] Hence, \[PE_s=\frac 12 (2000)(0.02)^2=\boxed{0.4\,\rm J}\]
Problem (3): An object with unknown mass is hung from a vertical spring with the spring constant $350\,\rm N/m$ so that it stretches the spring down by $7\,\rm cm$. What is the object's mass?
Solution: The spring is attached to the ceiling. Two forces are acting on the object. one is the gravitational force $F_g=mg$ downward, and the other is the spring force $F_s=kx$ upward. Balancing these two forces gives us a relation that by solving it for the unknown mass $m$, we will have \begin{align*} F_s &=F_g \\ kx&=mg \\ \Rightarrow m&=\frac{kx}{g} \\\\ &=\frac{350\times 0.07}{10} \\\\ &=\boxed{2.45\,\rm kg} \end{align*} It is worth noting that the minus sign in the original form of Hooke's law, $F_s=-kx$, shows us that the direction of the applied force by the spring on the object and its displacement is always in the opposite direction. In this case, the object pulls down the spring by its weight until it reaches a position where it no longer moves down.
Thus, the spring displacement is downward, so the force that the spring applies to the suspended object must be upward, according to Hooke's law. That is the meaning of the negative sign in the equation $F_s=-kx$.
Problem (4): A trampoline has a spring stiffness constant $k=4500\,\rm N/m$. A person weighing $780\,\rm N$ stands on it. How far will the trampoline go down?
Solution: The trampoline acts like a compressed spring. The trampoline goes down as much as the person's weight is balanced by the spring force the trampoline exerts on the person, $kx=mg$. Thus, we get \begin{align*} x&=\frac{mg}{k} \\\\ &=\frac{780}{4500} \\\\&=\boxed{0.17\,\rm m} \end{align*} Hence, the trampoline goes down as much as about $17\,\rm cm$.
Problem (5): The spring constant of a horizontal spring is $150\,\rm N/m$.
(a) How much force is required to compress it $35\,\rm cm$?
(b) How much work is done on the spring during this displacement?
Solution: The spring constant $k$ and the displacement value of the spring from its equilibrium position ($x=0$) are given.
(a) According to Hooke's law, the magnitude of the spring force is given by $F_s=kx$. Thus, we have \[F_s=150\times 0.35=\boxed{52.5\,\rm N}\]
(b) The work done by a spring is found using the formula $W=\frac 12 kx^2$. Therefore, substituting the values into it we have \[W=\frac 12 (150)(0.35)^2 =\boxed{9.2\,\rm J} \]
Problem (6): An object of mass $0.45\,\rm kg$ is hung from the end of a vertical spring that is attached to the ceiling. The object is allowed to lower slowly to an equilibrium point by a distance of $3\,\rm cm$. What is the value of the spring constant?
Solution: In this problem, the hanging object stretches down the spring due to its weight. On the other side, an upward force must be applied to the object to balance with the downward gravitational force. This force obeys Hooke's law.
According to Newton's second law, at the equilibrium point, the net force on the suspended object must be zero. The upward spring force $F_s=kx$ and the downward gravitational force $F_g=mg$ are acting on the object. Balancing these two forces and solve for the spring constant $k$ as below \begin{align*} kx&=mg \\\\ k&=\frac{mg}{x} \\\\ &=\frac{0.45\times 9.8}{0.03} \\\\&=\boxed{147\,\rm N/m} \end{align*} Try to remember this equation for an object suspended from or placed on top of a vertical spring in all Hooke's law problems.
We emphasize again that the negative sign in the spring force formula $F_s=-kx$ is removed during the calculation. The minus sign only shows us the direction of the spring force.
Problem (7): The spring constant of a spring is $150\,\rm N/m$. Find the magnitude of the force required to (a) compress the spring by $2.4\,\rm cm$ from its unstretched position, and (b) stretch the spring by $4.5\,\rm cm$ from its unstretched length.
Solution: Hooke's law relates the force that a spring exerts on an object when it is displaced from its unstretched position by $x$ as below \[F_s=-kx\] The negative in Hooke's law indicates the direction of the applied force on the object by the spring is always in the opposite direction of its displacement.
Usually, in all Hooke's law problems, the magnitude of the spring force is required such that the negative is removed.
(a) The spring compresses by $x=2.4\,\rm cm$, so the required force to provide this displacement is \[F=150\times (0.024)=\boxed{3.6\,\rm N}\]
(b) Similarly, the required force to stretch such spring by $x=4.5\,\rm cm$ is calculated as below \[F=150\times (0.045)=\boxed{6.75\,\rm N}\] Note that in the above, we converted all displacements into their SI unit, meters, by dividing by $100$.
Problem (8): A stone of mass $4\,\rm kg$ rests on a vertical spring. The spring is compressed $8\,\rm cm$ by the stone.
(a) What is the spring constant?
(b) The stone is pushed down an additional $2\,\rm cm$ and released. How much elastic potential energy has the spring just before that release?
Solution: (a) The stone is placed on a vertical spring. The upward spring force $F_s$ balances with the downward weight force $F_g$. From this we have \begin{align*} F_s&=F_g \\ kx&=mg \\ k&=\frac{mg}{x} \\\\ &=\frac{4\times 9.8}{0.08} \\\\ &=\boxed{490\,\rm N/m} \end{align*}
(b) This part is related to a question about elastic potential energy. Recall that the spring potential energy of a compressed or stretched spring by $x$ is given by the following formula \[PE_s=\frac 12 kx^2\] Note that $x$ is the distance value that the spring is displaced from its unstretched length or its equilibrium point.
In this case, after that additional pushing down, the spring has a total distance of $8+2=10\,\rm cm$ from the unstretched length. Therefore, we have \[PE_s=\frac 12 (490)(0.10)^2=\boxed{2.45\,\rm J}\]
Problem (9): A $6-\rm kg$ fruit basket full of apples is suspended motionless from a spring scale whose spring constant is $450\,\rm N/m$. By how much is the spring stretched down?
Solution: We want to solve this question differently. Here, we are going to speak more about the negative sign of Hooke's law and its role in solving problems.
We know that the minus sign in the equation $F_s=-kx$ is nothing but indicates the direction of the force applied by the spring is in the opposite direction of its displacement from its unstretched length.
If we want to solve Hooke's law problems by vector methods, that negative must be considered.
In the vector method, first, choose a positive direction. Let $y=0$ be our assumed origin and choose up to be the $+y$ direction.
Analysis (1): The basket is motionless, so the net force on it must be zero. The downward weight force and upward spring force acting on the basket must be balanced to produce a net zero force (zero acceleration).
Analysis (2): The spring is stretched down, so it has a negative displacement (going down in the $-y$ direction). According to the negative sign in Hooke's law, the spring force must be directed upward with a magnitude of $kx$, in agreement with the analysis (1).
Now apply Newton's second law in its vector form as $\vec{F}_{net}=m\vec{a}$ where $a=0$. \begin{gather*} \vec{F}_{net}=0 \\\\ \vec{F}_s+\vec{F}_g=0 \\\\ kx+(-mg)=0 \\\\ \Rightarrow \quad x=\frac{mg}{k} \end{gather*} Substituting the numerical values into this, we get \[x=\frac{6\times 9.8}{450}=\boxed{0.13\,\rm m}\] Thus, the spring of the scale goes down by $13\,\rm cm$.
Problem (10): A $250-\rm N$ force stretches a horizontal spring $25\,\rm cm$.
(a) Calculate the spring constant of the spring?
(b) How far would the spring stretch if a force of $150\,\rm N$ applied to it?
Solution: (a) With the given information first find the spring constant using Hooke's law as below \begin{align*} k&=\frac{F_s}{x} \\\\ &=\frac{250}{0.25} \\\\ &=\boxed{1000\,\rm N/m} \end{align*} This is the spring constant of this spring which does not changes by applying other forces.
(b) In this case, the applied force on the spring is changed as $F_s=150\,\rm N$, and we are asked for the spring displacement value from its unstretched length. Again, apply Hooke's law formula and solve for the displacement value $x$ \begin{align*} x&=\frac{F_s}{k} \\\\ &=\frac{150}{1000}\\\\ &=\boxed{0.15\,\rm m} \end{align*} Thus, applying such force can stretch the spring as far as $15\,\rm cm$ from its unstretched length.
Problem (11): A coil spring is $35\,\rm cm$ long when a weight of $25\,\rm N$ is hung from its free end and $36\,\rm cm$ when the weight is changed to $55\,\rm N$. Calculate the spring force constant of the spring.
Solution: Here, the natural or unstretched length of the spring is not given, but rather, its elongated length.
Given that the spring extends fro$m35\,\rm cm$ to $36\,\rm cm$ when the weight changes from $25\,\rm N$ to $55\,\rm N$, we can calculate the change in force $\Delta F$ and the change in length $\Delta x$: \begin{gather*} \Delta F = 55\,\rm N - 25\,\rm N = 30\,\rm N \\ \Delta x = 36\,\rm cm - 35\,\rm cm = 1\,\rm cm = 0.01\,\rm m \end{gather*} Substituting these values into the formula gives: \[k = \frac{\Delta F}{\Delta x} = \frac{30\,\rm N}{0.01\,\rm m} = 3000\,\rm N/m\] So, the spring force constant of the spring is $3000\,\rm N/m$.
Problem (11): A $75-\rm kg$ person slowly adds his weight to a vertical spring attached to the ceiling. The mas-spring system reaches an equilibrium point by stretching the spring down by $2.8\,\rm cm$ beyond that the spring no longer goes down further.
(a) Calculate the spring constant.
(b) A second identical spring is added to the previous one in parallel. This time, again, the person adds his weight to the combined springs. By how much will the combined springs be going down?
Solution: Again, we have Hooke's law problem that must be solved by considering the downward weight force $F_g=mg$.
(a) In this part, an object is hung from a spring attached to the ceiling. Thus, balance the upward spring force $F_s$ with the downward weight force $F_g$ at the equilibrium point and from that solve for the spring constant $k$ as below \begin{align*} F_s&=F_g \\ kx&=mg \\ \Rightarrow k&=\frac{mg}{x} \\\\ &=\frac{75\times 9.8}{2.8\times 10^{-2}} \\\\ &=\boxed{26250\,\rm N/m} \end{align*}
(b) The purpose of this section is to analyze springs in a parallel configuration. Here, we have two identical springs attached to the ceiling and a weight is hung from both. We want to examine the behavior of such systems.
In this case, two upward spring forces balance the downward force of gravity (weight). Apply Newton's second law to the object and solve for the unknown common displacement of the springs. Therefore, \begin{align*} F_g&=F_{s1}+F_{s2} \\\\ mg&=kx+kx \\\\ \Rightarrow x&=\frac{mg}{2k} \\\\&=\frac{75\times 9.8}{2\times 26250} \\\\&=\boxed{0.014\,\rm m} \end{align*} Therefore, The springs go down as much as $1.4\,\rm cm$.
Keep in mind that because the two springs are identical, their displacements from the equilibrium point are the same. That's why we assumed $x_1=x_2=x$ for both springs.
Problem (12): A $0.45\,\rm kg$ object is attached to a horizontal spring with a force constant of $k=600\,\rm N/m$. It is displaced from its unstretched length (or equilibrium) and then released. Find the period and frequency of oscillations of the object.
Solution: In all simple harmonic motion problems, Hooke's law is used to derive the frequency $f$ and period $T$ of the oscillating object attached to a spring. In summary, the following formulas can be used \[f=\frac{1}{T}=\frac{1}{2\pi}\sqrt{\frac{k}{m}}\] Substituting the values into this equation, we get \[f=\frac{1}{2\pi}\sqrt{\frac{600}{0.45}}=\boxed{5.8\,\rm Hz}\] and the inverse of frequency gives us the period of oscillations as below \[T=\frac 1f=\boxed{0.17\,\rm s}\] Therefore, when the object attached to this spring is displaced from its unstretched length, every $1\,\rm s$ it will have six times complete back and forth movement. In other words, it oscillates with a frequency of about $6$ hertz, the SI unit of frequency.
The period of oscillation for this object also means that it completes a back-and-forth motion in about $0.17\,\rm s$.
Problem (13): We want to compress a light spring with spring constant $k=25\,\rm N/m$ by $10\,\rm cm$.
(a) How much force is required to accomplish this?
(b) How much work is done on the spring?
Solution: Hooke's law gives us a relation between the magnitude of the spring force exerted on an object and the displacement of the spring, $F=kx$. Notice that we removed the minus sign in the original Hooke's law since we want the spring force's magnitude.
The other point about this formula is that $F$ is always the maximum force the spring exerts on any block attached to it during a distance of $x$.
(a) Thus, the maximum force is found to be \[F=25\times (0.10)=\boxed{2.5\,\rm N} \]
(b) The work done by a spring does not obey the work formula we practiced in the section on work problems in physics. Because, in this case, the spring force is a varying force.
Overall, keep in mind the work done by a spring on any object during a displacement of $x$ is calculated as below \[W_s=-\frac 12 kx^2\] And the work done by any external agent (like us) to stretch or compress the spring by a distance of $x$ is the negative of the work done by the spring on the object \[W_s=-W_{ext}\]
(b) According to the above, we have \begin{align*} W_{ext}&=\frac 12 kx^2 \\\\ &=\frac 12 (25)(0.10)^2 \\\\ &=\boxed{0.125\,\rm J} \end{align*} Thus, we must spend $0.125\,\rm J$ of energy to compress or stretch this spring by $0.10\,\rm m$.
Or, it can be said the work done by the spring on the object in stretching or compressing by 10 cm is about $-2\,\rm j$.
Summary:
In this short course, we explored Hooke’s law by solving various problems. We learned that Hooke’s law establishes a relationship between the spring force $F_s$, the spring constant $k$, and the displacement $\Delta x$ of the spring from its equilibrium position, expressed as $F_s=−k\Delta x$. The negative sign in Hooke’s law signifies that the spring force $F_s$ is a restoring force, meaning it acts in the opposite direction of the spring’s displacement. This is a key characteristic of Hooke’s law problems
Author: Dr. Ali Nemati
Published: 8/24/2022
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
