Snell's law practice problems with answers
Are you seeking practice problems to help with your homework, or perhaps a deeper understanding of Snell’s law? This comprehensive guide provides everything you need to know about Snell’s law, from problem-solving techniques to fundamental concepts. It’s a one-stop resource for all your needs.
By the way, if you’re taking the AP Physics 1 exam this year, be sure to use this ultimate AP Physics 1 formula sheet. It’s a valuable resource.
Snell's Law Practice Problems
Problem (1): A beam of flashlight traveling in air incident on the surface of a thin glass at an angle of $38^\circ$ with the normal. The index of refraction of the glass is $1.56$. What is the angle of refraction?
Solution: When a beam of light strikes the boundary between two different media, such as air and glass, part of it is reflected, and another part is refracted.
The portion that enters the other side of the boundary is called the refracted ray. The angle that this ray makes with the normal to the boundary is known as the angle of refraction.
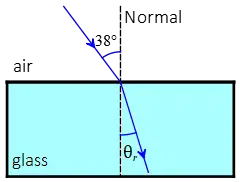
In this example problem, the light is initially in the air with an index of refraction $n_i=1.00$ and strikes the boundary surface separating air and glass at an angle of incidence $\theta_i=38^\circ$. The subscript $i$ denotes the incident.
The other medium is glass with $n_r=1.56$. The refracted ray lies within it at an unknown angle $\theta_r=?$, which should be found using Snell's law of refraction.
Before going further and solving the problem, we expect that since the light beam enters from a medium with a low index of refraction (air) into one with a high index of refraction (glass), the refracted ray should be bent toward the normal.
By applying Snell's law, we can verify this claim. \begin{align*} n_i \sin\theta_i&=n_r\sin\theta_r\\\\ (1.00)\sin 38^\circ&=(1.56)\sin\theta_r\\\\\Rightarrow \sin\theta_r&=\frac{1.00}{1.56}\sin 38^\circ\\\\&=0.3947\end{align*} Now, we find the angle whose sine is $0.3947$: \begin{align*} \sin\theta_r&=0.3947\\ \Rightarrow \theta_r&=\sin^{-1}(0.3947)\\&=23.25^\circ\end{align*} As expected, the refracted ray is bent towards the normal.
Problem (2): A boy is in a pool and shines a flashlight toward the level of it at a $35^\circ$ angle to the vertical. At what angle does the flashlight beam leave the pool? (the index of refraction of glass is $1.33$).
Solution: As before, a beam of light strikes the surface boundary of two different media, so we must use Snell's law to find the refracted angle in the air.
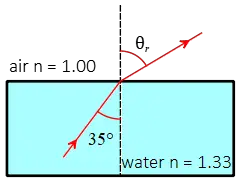
Contrary to the previous problems, here the light beam initially travels in the glass and enters the air, which has a lower index of refraction. Therefore, we expect that the angle of refraction in the air will bend away from the normal.
In other words, we expect that the angle of refraction will be greater than the angle of incidence, i.e., $\theta_r>\theta_i$. Now, we calculate it by applying Snell's law formula as below: \begin{align*} n_i \sin\theta_i&=n_r\sin\theta_r\\\\ (1.33)\sin 35^\circ&=(1.00)\sin\theta_r\\\\\Rightarrow \sin\theta_r&=\frac{1.33}{1.00}\sin 35^\circ\\\\&=0.7629\end{align*} The angle whose sine is $0.7629$ is found as below \begin{align*} \sin\theta_r&=0.7629 \\ \Rightarrow \theta_r&=\sin^{-1}(0.7629)\\&=49.72^\circ\end{align*} As expected, the refracted ray bends away from the normal.
One of the applications of Snell's law is in solving a phenomenon in physics called total internal reflection. For more practice, refer to the following page:
Total internal reflection on problems and solutions
Problem (3): A slab of glass has an index of refraction of 1.5 and is submerged in water with $n=1.33$. A beam of monochrome light is incident on the slab and is refracted.
(a) Find the angle of refraction if the angle of incidence is $30^\circ$.
(b) Now, assume that the light is initially in the glass and incident on the glass-water surface. What is the refraction of light?
Solution: (a) A beam of light strikes the boundary between water ($n_i=1.33$) and glass ($n_r=1.5$) at point A at an angle of incidence $\theta_i=30^\circ$. Applying Snell's law of refraction, $n_i \sin \theta_i=n_r \sin \theta_r$, at the surface where the light enters the glass, we can solve for the unknown refracted angle as follows: \begin{align*} \sin\theta_r&=\frac {n_i}{n_r}\sin \theta_i \\\\ &=\frac{1.33}{1.5}\sin 30^\circ \\\\ &=0.443\end{align*} Therefore, the angle of refraction is $\theta_r=26.3^\circ$.
(b) In the second case, the light originates from the glass ($n_i=1.5$) and strikes the boundary with water ($n_r=1.33$) at an angle of incidence of $30^\circ$. Using Snell's law equation, we can calculate the angle of refraction in the water: \begin{align*}n_i\sin\theta_i&=n_r\sin\theta_r\\\\ (1.5)\sin 30^\circ&=(1.33)\sin\theta_r\\\\\Rightarrow \sin\theta_r&=\frac{1.5}{1.33}\sin 30^\circ\\\\&=0.563\end{align*} Thus, the angle of refraction in the water is $34.3^\circ$.
Problem (4): A beam of light traveling in the air, strikes a flat slab of glass at an incident angle of $30^\circ$. The index of refraction of the glass is $1.5$. At the moment of leaving the glass, what is the angle of refraction?
Solution: In this problem, we must apply Snell's law twice —once for the entering stage at the air-glass interface and the second for the exiting stage at the glass-air interface.
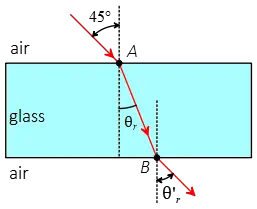
In the first stage, the incident beam is in the air ($n_i=1.00$) and strikes at point $A$ with an angle of incidence of $45^\circ$. The refracted beam lies inside the glass ($n_r=1.5$) with an unknown refracted angle $\theta_r$. This can be determined as follows: \begin{align*} n_i \sin\theta_i&=n_r\sin\theta_r\\\\ (1.00)\sin 45^\circ&=(1.5)\sin\theta_r\\\\\Rightarrow \sin\theta_r&=\frac{1.00}{1.5}\sin 45^\circ\\\\&=0.4715\end{align*} Therefore, the first refracted angle, which occurs in the slab of glass, is $\theta_r=28.13^\circ$.
For the second stage, the beam of light inside the glass strikes the glass-air interface at point $B$ with an angle of incidence of $28.13^\circ$. The refracted beam enters the air ($n_r=1.00$) with an unknown angle $\theta'_r$, which can be found as follows: \begin{align*} n_i \sin\theta_i&=n_r\sin\theta'_r\\\\ (1.5)\sin 28.13^\circ&=(1.00)\sin\theta'_r\\\\\Rightarrow \sin\theta'_r&=\frac{1.5}{1.00}\sin 28.13^\circ\\\\&=0.7072\end{align*} Finally, the beam leaves the glass with an angle of refraction of $45^\circ$, which is the same as the angle of entering.
When a beam of light passes through a slab of any material with uniform thickness the angle of entering (incident angle) and the leaving angle (refracted angle) are the same.
Problem (5): A uniform rectangular block of glass ($n=1.56$) surrounded by some fluid with an index of refraction $n=1.63$. A beam of light strikes at point $A$ at an angle of $32^\circ$ to the normal. At what angle does the light beam leave the slab?
Solution: In this problem, we must apply Snell's law twice - at points $A$ and again at point $B$ - to determine the path of the refracted ray as it exits the slab. Snell's law is given by the equation $n_i \sin\theta_i=n_r\sin\theta_r$ where $n_i$ and $\theta_i$ are the index of refraction and angle of incidence of the medium where the ray originates, respectively.
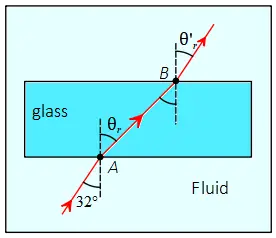
Similarly, $n_r$ and $\theta_r$ are the index of refraction and angle of refraction of the medium where the ray exits, respectively.
To find the angle of refraction at point $A$, We solve Snell's law for $\sin \theta_r$ as follows: \begin{align*} n_i \sin\theta_i&=n_r\sin\theta_r\\\\ (1.63)\sin 32^\circ&=(1.56)\sin\theta_r\\\\\Rightarrow \sin\theta_r&=\frac{1.63}{1.56}\sin 32^\circ\\\\&=0.5537\end{align*} Taking the inverse sine of both sides, we find the refracted angle at point $A$: \begin{align*}\theta_r&=\sin^{-1}(0.5537)\\&=33.62^\circ\end{align*} Now, the refracted ray acts as the incident ray and strikes point $B$ at an angle of incidence of $33.62^\circ$ to the normal. This ray is inside the glass with $n_i=1.56$. Again, applying Snell's law of refraction at point $B$, we have \begin{align*} n_i \sin\theta_i&=n_r\sin\theta'_r\\\\ (1.56)\sin 33.62^\circ&=(1.63)\sin\theta'_r\\\\\Rightarrow \sin\theta'_r&=\frac{1.56}{1.63}\sin 33.62^\circ\\\\&=0.5200\end{align*} Taking the inverse sine of both sides, we find \begin{align*}\theta'_r&=\sin^{-1}(0.5200)\\&=32.00^\circ\end{align*} Thus, as expected, the light beam leaves the slab at the same angle to the normal as the angle of incidence.
Problem (6): A beam of light incident on and deflected by a $30^\circ-60^\circ-90^\circ$ prism as shown in the figure. The deflected light makes an angle of $25^\circ$ with the direction of the incident ray. Using laws of refraction, find the prism's index of refraction.
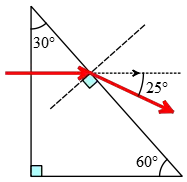
Solution: In this example problem, there are two boundary surfaces to consider. The first is the front face of the prism, where the original ray strikes at a normal angle, allowing it to enter the prism without deflection.
The second surface is the hypotenuse of the prism, where the previously reflected ray strikes and undergoes final deflection by the prism.
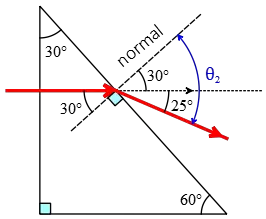
Since the final refraction occurs on the hypotenuse, we first draw the normal to it. From the resulting geometry, we can determine all the necessary components for applying Snell's law, i.e., the angles of incidence and refraction.
From geometry, we can see the ray's angle of incidence on the hypotenuse is the same as the apex angle of the prism, i.e., $\theta_1=30^\circ$.
The ray exits the prism at an angle of $\theta_2$, which, according to the geometry, is the sum of the deflection angle ($25^\circ$) and the angle of incidence ($30^\circ$), i.e., $\theta_2=25^\circ+30^\circ=55^\circ$. By substituting these values, along with the index of refraction for air ($n_2=1.00$), into Snell's law, we can find $n_1$ for the prism. \begin{align*} n_1\sin\theta_1&=n_2\sin\theta_2\\\\n_1(\sin 30^\circ)&=(1.00)(\sin 55^\circ)\\\\\Rightarrow n_1&=\frac{(1.00)(\sin 55^\circ)}{\sin 30^\circ}\\\\&=1.63 \end{align*} Note that to apply Snell's law, we must determine all angles with respect to the normal to the boundary between two different media.
Author: Dr. Ali Nemati
Date Published: 5/8/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
