Total Internal Reflection Problems and Solutions
On this page, all aspects of the total internal reflection phenomenon are explored in the form of problem-solving.
For reference, total internal reflection occurs when the incident light is in a medium with a higher index of refraction.
In this situation, if the angle of incidence is greater than the critical angle, then the refracted ray totally internally reflected back into the original medium.
Total Internal Reflection Problems
Problem (1): An unknown glass has an index of refraction of $n=1.5$. For a beam of light originating in the glass, at what angles does the light $100\%$ reflected back into the glass? (The index of refraction of air is $n_{air}=1.00$).
Solution: When light moves through a medium with an index of refraction $n_1$ and strikes a boundary of a region with an index of refraction $n_2$ such that $n_1>n_2$, then total internal reflection can occur if the incident angle equals or is greater than a critical angle $\theta_c$ given by the following formula \[\sin\theta_c=\frac{n_2}{n_1}\] If the incident ray equals the critical angle, then the refracted ray exit along the boundary at the angle of $90^\circ$.
For incident angles greater than the critical angle, $\theta_1 >\theta_c$, the refracted ray vanishes at the boundary, and $100\%$ is reflected back into the original medium. This process is called total internal reflection.
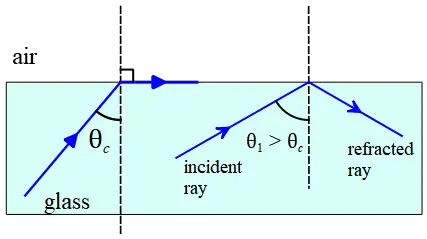
In this problem, we are told that light is initially in a medium with a higher index of refraction and wants to enter a medium with a lower index of refraction. So, the necessary condition for occurring total internal reflection is satisfied.
Thus, we must first find the critical angle whose magnitude is obtained as below \[\sin\theta_c=\frac{n_{air}}{n_{glass}}=\frac{1}{1.5}\] Taking the inverse of the sine of both sides, gives \[\theta_c=\sin^{-1}\left(\frac{1}{1.5}\right)=41.8^\circ\] Hence, if the angle of incidence in the glass exceeds about $42^\circ$, then all incident rays completely return back into the same medium.
Problem (2): A ray of light traveling through glass with an index of refraction $n=1.5$ strikes the interface of the glass-water. Let the index of refraction of water be $n=1.33$. At what angle, the ray does not enter the water?
Solution: We want no ray to exist in the water. We know that when a ray of light strikes a boundary of two different media, part of it is reflected back into the same medium and part of the ray enters the second medium (or refracted).
In this question, we are asked to find an angle at which the refracted ray is removed. This occurs when the refracted angle in the second medium (here, water) becomes greater than or equal to $90^\circ$. Applying Snell's law of refraction, we have \begin{align*} n_1 \sin\theta_1&=n_2 \sin\theta_2\\\\ (1.5)\sin\theta_1&=(1.33)\sin 90^\circ\\\\ \Rightarrow \quad \sin\theta_2&=\frac{1.33}{1.5}\sin 90^\circ\\\\&=0.887\end{align*} Next, take the inverse of the sine to find the angle whose sine is $1.128$ \[\theta_2=\sin^{-1}(0.887)=62.5^\circ\] This incident angle at which the refracted angle becomes $90^\circ$ is called the critical angle. Any ray, in the glass, striking the boundary with an angle that exceeds 40 degrees, totally returns back into the same original medium. This phenomenon is also called total internal reflection.
Problem (3): Find the critical angle for a ray of light traveling from Ethyl alcohol to Benzene. Ethyl alcohol has an index of refraction $n=1.361$ and Benzene has $n=1.501$.
Solution: There occurs no totally internal reflection because there is no critical angle for this configuration. In this scenario, light is traveling from a rare medium (low $n$) to a dense medium (with high $n$) and this is contrary to the criteria for the formation of a total internal reflection.
Thus, total internal reflection occurs when light traveling in a medium strikes the boundary of a medium whose index of refraction is higher than the original medium.
Problem (4): The speed of sound in a room filled with air is $343\,{\rm m/s}$. The walls of this room are made of concrete, in which the speed of sound is $1850\,{\rm m/s}$.
(a) Find the critical angle for total internal reflection of sound waves striking the air-concrete interface.
(b) If we want the sound to undergo total internal reflection, in which medium must it be traveling?
Solution: To find the critical angle for a total internal reflection problem, we must use the following equation \[\theta_c=\sin^{-1}\left(\frac{n_{rare}}{n_{dense}}\right)\] But in this question, neither of indices of refraction are given.
Recall that Snell's law of refraction is also written in terms of velocities instead of indices of refraction. Thus, the alternate form of Snell's law is given by the following equation \[\frac{\sin\theta_1}{\sin\theta_2}=\frac{v_1}{v_2}\] where the subscripts $1$ and $2$ refer to the incident and refracted rays.
(a) We know that the critical angle is the angle at which the refracted ray becomes $90^\circ$. So, setting $\theta_2=90^\circ$ in the above equation, and solving for $\theta_1=\theta_{cri}$, we get \begin{align*} \sin\theta_{cri}&=\sin\theta_2 \left(\frac{v_1}{v_2}\right)\\\\&=\sin 90^\circ \left(\frac{343}{1850}\right)\\\\&=0.186 \end{align*} Now, take the inverse of sine from both sides to find the angle whose sine is $0.186$ \[\theta_{cri}=\sin^{-1}(0.186)=10.7^\circ\] Hence, if the sound waves strike the wall at angles greater than about $11^\circ$, then all is reflected back into the wall without any waves passing through the wall.
(b) As you know, total internal reflection occurs when mechanical waves (sound) or electromagnetic waves (light) are incidents on a boundary of a medium having a lower index of refraction than the original medium.
We can modify the above statement to accommodate the velocities in both mediums where the indices of refraction are not known. In this case, the total internal reflection occurs when the waves strike the boundary of a medium, in which the speed of the waves is greater than the original medium.
In this problem, the total internal reflection can occur when sound waves travel from the air and strike the wall at an angle greater than the critical angle found above, i.e. $\theta>10.7^\circ$.
Problem (5): The boundary of the two mediums is shown in the figure below. The angle of incidence with the horizontal is $30^\circ$. The incident ray refracted parallel to the interface. Find the index of refraction of the second medium.

Solution: We are told in the problem that the refracted ray is parallel to the boundary of two mediums. We know that this situation always occurs when the incident ray is in a dense medium and strikes the boundary of a less dense medium.
So, the second medium must have a lower index of refraction than the original medium. Note that the incident angle is measured with a line perpendicular to the boundary. Here, the incident angle is $\theta_1=90^\circ-30^\circ=60^\circ$.
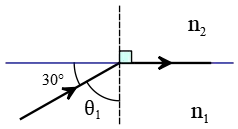
Setting the refracted angle as $\theta_2=90^\circ$ in Snell's law of refraction, and solving for the index of refraction $n_2$, we will have \begin{align*} n_1 \sin\theta_1&=n_2\sin\theta_2\\\\\sqrt{3}\sin 60^\circ&=n_2 \sin 90^\circ\\\\ \sqrt{3}\left(\frac{\sqrt{3}}2\right)&=n_2\\\\\Rightarrow n_2 &=\frac 32 \end{align*} As expected, the second medium must be less dense than the first medium.
Problem (6): A beam of light moves from air into an unknown glass. The angle of incidence is $30^\circ$, and the angle of refraction is $22^\circ$. For a beam of light originating from the glass, find the critical angle.
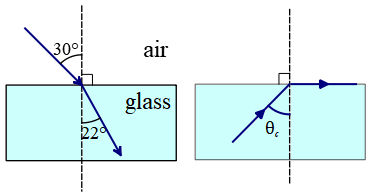
Solution: Critical angle is defined when a ray travels in a dense medium and strikes a boundary with a lower index of refraction. Its magnitude is calculated as \[\theta_c=\sin^{-1}\left(\frac{n_2}{n_1}\right)\] where always $n_1>n_2$.
When a beam of light strikes the interface of the two media at the critical angle, the refracted ray exits parallel to the boundary. In this case, the refracted angle is $90^\circ$.
Here, we want to find the critical angle when the light is in the glass and enters the air. The index of refraction of the glass is unknown.
From the first part of the question, we can find the glass's index of refraction by applying Snell's law of refraction. \begin{align*} n_1 \sin\theta_1&=n_2 \sin\theta_2\\\\ (1)\sin 30^\circ&=n\sin 22^\circ\\\\ \Rightarrow \quad n&=\frac{\sin 30^\circ}{\sin 22^\circ}(1)\\\\&=\frac{0.5}{0.375}\\\\&=1.33 \end{align*} By having the index of refraction of the glass, the critical angle is found for this total internal reflection problem from the following equation \[\theta_c=\sin^{-1}\left(\frac{n_2}{n_1}\right)=\sin^{-1}\left(\frac{1.00}{1.33}\right)=48.8^\circ\] Thus, if light originated from the water incident on the boundary of air at an angle greater than about $49^\circ$, then light is totally returned back into the water and does not enter the air.
Problem (7): The critical angle of a specific glass in the air is $\theta_c=37.8^\circ$. Now suppose that we put it into a tank of water. What will change its critical angle?
Solution: In the first case, the boundary is composed of glass-air. Using critical angle formula, we have \[\sin\theta_c=\frac{n_{air}}{n_{glass}}\] In the second case, the glass surrounded by a water. So, the interface is glass-water. Again, its critical angle is found as \[\sin\theta'_c=\frac{n_{water}}{n_{glass}}\] The index of refraction of the glass is unknown. Dividing the second relation by the first one, gives \[\frac{\sin\theta'_c}{\sin\theta_c}=\frac{n_{water}}{n_{air}}\] Setting $n_{water}=1.33$ and solving for the unknown angle $\theta'_c$, we get \begin{align*} \sin\theta'_c&=\sin\theta_c \left(\frac{n_{water}}{n_{air}}\right)\\\\&=\sin(37.8^\circ)\frac{1.33}{1.00}\\\\&=0.816\end{align*} Take the inverse sine of both sides to find the angle whose sine is $0.816$ \[\theta'_c=\sin^{-1}(0.816)=54.7^\circ \]
Problem (8): A light bulb is placed 5 meters below a swimming pool. What is the diameter of the circle of light formed on the surface seen directly from above?
Solution: We can assume the light bulb to be a point source. Rays emit in all directions from that point source and strike the water-air interface. Some rays are incident on the boundary at less than the critical angle, refracted, and enter the air.
The rays have an incident angle greater than the critical angle, do not enter the air, and $100\%$ reflect back into the water.
These completely reflected rays are responsible for the formation of a circle of light on the surface of the water.
The diameter of the circle of light is the distance between the two points at which the rays reach the surface at the critical angle. First, using critical angle formula, we find it as below \[\theta_c=\sin^{-1}\left(\frac{1.00}{1.33}\right)=48.7^\circ\] As you can see from the geometry, and using the definition of sine function, the radius of the circle of light is found as \[\sin\theta_c=\frac{r}{H} \Rightarrow r=H\sin\theta_c\] where $H$ is the pool's depth. So, the radius or diameter of the circle $D=2r$ is computed as below \[D=2H\sin\theta_c=2(5)(\sin 48.7^\circ)=7.5\,{\rm m}\]
Problem (9): A beam of light is incident on the surface $AB$ of a prism surrounded by air at the critical angle, as shown in the figure. Find the angle of incidence, $\theta_1$.
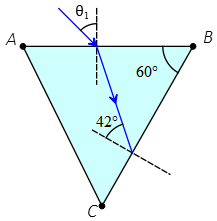
Solution: we are told that the ray is incident on the surface $BC$ at the critical angle. Thus, the refracted ray must be parallel to $BC$.
To find the critical angle in a total internal reflection problem, using Snell's law, we arrive at the following formula \[\sin\theta_c=\frac{n_{rare}}{n_{dense}}\] Here, the prism is surrounded by air, so $n_{rare}=1.00$. The index of refraction of the prism, $n_p$, is not given.
Thus, the critical angle at the boundary of $BC$ is found as below \[\sin 42^\circ=\frac{1}{n_p} \quad (I)\] Now, we must apply Snell's law at the entering point into the prism for the incident ray, but the angle of refraction at that point is not known.
From geometry of the figure, we have $\beta=90^\circ-42^\circ=48^\circ$. On the other, recall that the sum of angles of a triangle equals $180^\circ$.
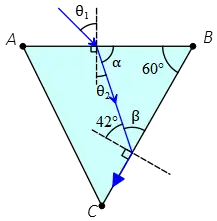
Thus, the angle $\alpha$ is determined as below \begin{gather*} \alpha+\beta+60^\circ=180^\circ \\ \alpha+48^\circ+60^\circ=180^\circ\\\Rightarrow \quad \alpha=72^\circ\end{gather*} Now that we have angle $\alpha$, the refracted ray at the entering surface $AB$ is simply found as below \[\theta_2+\alpha=90^\circ \Rightarrow \theta_2=18^\circ\] Applying Snell's law at this surface $AB$, we get \begin{align*} n_1 \sin\theta_1&=n_2 \sin\theta_2 \\\\ (1)\sin\theta_1 &=n_p \sin 18^\circ \quad (II) \end{align*} From equation $(I)$, the index of refraction of prism is $n_p=\frac{1}{\sin 42^\circ}$. Substituting this into equation $(II)$, we can get the incident angle as below \begin{align*} \sin\theta_1 &=\frac{\sin 18^\circ}{\sin 42^\circ}\\\\&=0.462 \end{align*} By taking the inverse of sine from both sides, we can find the angle whose sine is $0.461$ \[\theta_1=\sin^{-1}(0.461)=27.5^\circ\]
Summary
In this article, some problems about total internal reflection were presented along with detailed solutions.
The necessary conditions for total internal reflection are as below:
(1) Light must travel from a denser medium to a rare medium.
(2) The angle of incidence in the denser medium must be greater than the critical angle at the boundary of the two media.
Author: Ali Nemati
Date Published: 9/3/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
