Simple Harmonic Motion Problems for High Schools
Simple harmonic motion is defined as a kind of motion in which the net force along the motion obeys Hooke's law.
According to Hooke's law, the net force is proportional to the displacement from the equilibrium point and is always directed toward that point. \[F_{net}=-kx\]
This article teaches all concepts relating to simple harmonic motion (SHM) by problem-solution strategy.
In the following, some problems on simple harmonic motion are solved. All problems are for the AP Physics 1 exam and/or high school students.
Simple Harmonic Motion (SHM) Problems
Problem (1): A 0.50-kg object is attached to a horizontal spring whose spring constant is k=300 N/m and is undergoing a simple harmonic motion. Calculate its
(a) Period, (b) frequency, (c) angular frequency.
Solution: Imagine an object is attached to an unstretched spring, displaces the spring from its equilibrium, and then releases. After releasing, the object undergoes a simple harmonic motion. The period and frequency of such simple harmonic motion are obtained by the following formula \[T=2\pi\sqrt{\frac{m}{k}}\quad,\quad f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}\] where $m$ is the mass of the object and $k$, is a constant that indicates the stiffness of the spring, called the spring constant.
(a) Substituting the values into the above formula for the period, we have \[T=2\pi\sqrt{\frac{0.5}{300}}=0.256\quad {\rm s}\]
(b) To find the frequency, we can use the formula above or use $f=1/T$, instead. Thus, \[f=\frac{1}{0.256}=3.9\quad {\rm Hz}\] Note that the SI unit of frequency is Hz.
(c) Angular frequency is related to the frequency or period of oscillation as $\omega=2\pi f=2\pi/T$. Therefore, \[\omega=2\pi f=2\pi(3.9)=24.5\,{\rm \frac{rad}{s}}\] The SI unit of angular frequency is radians per second, $rad/s$.
Problem (2): A scale is stretched by 3.2 cm when a 2.4 kg object is attached.
(a) Find the spring stiffness constant.
(b) Now suppose the object is lowered downward from its rest by as much as 2 cm and released. Find the period and frequency of the oscillations.
(c) Write down the vertical displacement vs. time equation for this system.
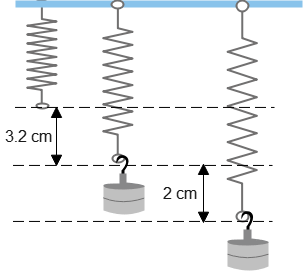
Solution: The spring-mass system has a simple harmonic motion in which the period and frequency of oscillations are given by the following formula \[T=2\pi\sqrt{\frac{m}{k}}\quad,\quad f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}\] where $k$ is the spring stiffness constant.
(a) In this problem, $k$ is unknown and is found by applying Newton's second law of motion to the vertical forces, downward weight, and upward spring force, acting on the object. These forces are in balance because the object is at rest after stretching.
Thus, when a load is hung from a spring (say a scale), the spring constant is computed as below: [k=\frac{mg}{x_0}=\frac{(2.4)(9.8)}{3.2}=7.35\,({\rm N \cdot m^{-1}})\] In the above, $x_0$ is the maximum distance when a load stretches an unloaded spring.
(b) The initial configuration (after hanging an object from the scale) is at rest with no oscillations. This situation is called the equilibrium state.
Any agent that disrupts this situation can cause oscillations in the mass-spring system.
In this example problem, the object is pushed from its equilibrium point by $2\,{\rm cm}$ and comes to another rest. This maximum displacement is called the amplitude of the oscillations. Thus, $A=0.2\,{\rm m}$.
The period, which is the time required to complete one cycle, is obtained as below \[ T=2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{2.4}{7.35}}=3.6\,{\rm s}\] The frequency of the oscillations, which indicates the number of full cycles per second is the inverse of the period \[f=\frac{1}{T}=\frac{1}{3.6}=0.28\,{\rm Hz}\]
(c) The vertical displacement vs. time equation for a simple harmonic motion is as $y=A\sin(\omega t)$ or $y=A\cos(\omega)t$ which depends on the initial configuration of the system. $\omega=2\pi/T=2\pi f$ is the angular frequency.
The former case is for when the object is attached to an unstretched spring, i.e., $x_0=0$. The latter case is for an object that is hung from a stretched spring, i.e., $x_0\neq0$, see figures.
This spring-mass system starts its oscillations when the spring is initially stretched some length, so we must use the cosine function. \begin{align*} y&=A\cos\left(\frac{2\pi}{T} t\right)\\\\&= (0.2)\cos\left(\frac{2\pi}{3.6} t\right)\\\\&=(0.2\,{\rm m})\cos\left(\frac{5\pi}{9} t\right)\end{align*}
Problem (3): An object of 45 N is hanging from a spring vertically. The spring is stretched from its equilibrium point by 0.14 m. What is the spring constant?
Solution: The spring is initially unloaded and unstretched. Hanging a 45-N object from it causes it to stretch by 0.14 m. This system is at rest and, therefore, at equilibrium. Applying Newton's second law gives the following formula to find the spring stiffness constant \[k=\frac{mg}{x_0}=\frac{45}{0.14}=321.4 \, {\rm N\cdot m^{-1}}\] Note that $x_0$ is the length the unloaded spring is initially stretched by an object's weight.
Problem (4): A 2-kg block is attached to a spring whose constant is 32 N/m horizontally. Imagine it being displaced from equilibrium by 4 cm and released from rest. How much time does it take for the block to reach the point x=2 cm?
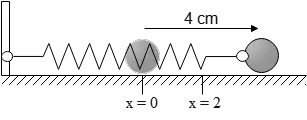
Solution: To find the required time, we must write down an equation in which the object's position at any instant of time is shown explicitly.
We know that a mass attached to a spring undergoes a simple harmonic motion (SHM) with the equation $x=A\cos\omega t$.
Above, $A$ is the maximum displacement from the equilibrium point of the spring-mass system, called the amplitude.
$\omega$ is also the angular frequency, which is related to period and frequency by $\omega=2\pi f=2\pi/T$.
The block's period of oscillation is found by \[T=2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{2}{32}}=\frac{\pi}{4}\,{\rm s}\] Therefore, the angular frequency is $\omega=2\pi/T=8\,{\rm rad/s}$.
In this example, the maximum distance (amplitude) from where the block is released at time $t=0$ is 4 cm, so $A=0.4\,{\rm m}$.
Substituting these quantities into the above equation of SHM yields $x=(0.4\,{\rm m})\cos(8t)$. This equation gives the location of the object at any instant of time.
If we put $x=0.2\,{\rm m}$ into the equation above and solve for the time $t$, it gives the time required to reach that point. \begin{align*} x&=0.4 \cos(8t)\\ 0.2&=0.4 \cos(8t)\\ \Rightarrow 1/2&=\cos(8t)\end{align*} Taking inverse trigonometric of both sides, gives \[8t=\cos^{-1}(1/2)=\pi/6 \Rightarrow t=\pi/48=0.06\,{\rm s}\] Hence, it takes 0.06 seconds for the object to reach the point located at x=2 cm.
Problem (5): An object hangs from a spring with a constant stiffness of 40 N/m and stretches it by 0.5 m.
(a) What is the mass of the hanging object? (take $g=10\,{\rm m/s^2}$)
(b) We pull the object $3\,{\rm cm}$ from its equilibrium position and release it. Find an equation for the position of the object as a function of time.
Solution: (a) Because the object is at rest, applying Newton's second law gives the equation $kx=mg$. Solving for the unknown mass $m$, we have \[m=\frac{kx}{g}=\frac{40\times 0.5}{10}=2\,{\rm kg}\]
(b) By doing this, the object oscillates around its equilibrium position. Here, $0.3\,{\rm m}$ is the maximum distance from that position, which is called the amplitude of oscillations.
The period of the oscillations is also obtained by the following formula: \begin{align*} T&=2\pi\sqrt{\frac{m}{k}}\\\\&=2\pi\sqrt{\frac{2}{40}}\\\\&=1.4\quad {\rm s}\end{align*} Thus, one complete cycle takes 2 seconds.
When an object at the maximum distance from its equilibrium starts its oscillation motion, then the standard equation of position vs. time is given by $y=A\cos(\omega t)$, where $\omega=2\pi/T$.
Therefore, the displacement vs. time equation for this object is as follows: \[y=(0.3\,{\rm m})\cos\left(\frac{10\pi}{7} t\right)\]
Problem (6): Consider placing a spring in a vertical position and putting a 100-g object on it. We see it compressed by 2 cm.
(a) If an additional load of 300 grams is placed on top of the previous object, how much will the spring compress this time?
(b) Find the spring constant.
Solution: This question is similar to the problems on Hooke's law, refer to that page and practice more. We must use Hooke's law twice. Here, the weight of the object, $W$, causes compression. The first object brings the spring to an equilibrium position, so $k\Delta x_1=W_1$.
The additional load also makes the displacement $k\Delta x_2=W_2$. Taking the proportions of these two equations and solving for the unknown displacement $\Delta x_2$, we have \begin{align*} \frac{k\Delta x_1}{k\Delta x_2}&=\frac{W_1}{W_2} \\ \\\Rightarrow \Delta x_2&=\frac{W_2 \Delta x_1}{W_1}\\\\ &=\frac{300\times 2}{100}\\\\&=6\quad {\rm cm}\end{align*} Therefore, the second object compresses the spring 6 cm from its previous position.
(b) The weight of the first load $(0.1\,{\rm kg})(9.8)=0.98\,{\rm N}$ causes the spring to compress by $0.2\,{\rm m}$. By applying Hooke's law, we can find the spring constant as below \[k=\frac{F}{x}=\frac{0.98}{0.2}=4.9\,({\rm N\cdot m^{-1}})\]
Problem (7): An object attached to a spring with a constant of 400 N/m vibrates at 36 Hz. If the stiffness of the spring is doubled, how would the oscillations change?
Solution: According to the frequency formula for a simple harmonic motion, $f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$, the frequency of vibrations is proportional to the square root of the spring's constant, i.e., $f\propto \sqrt{k}$. Thus, we would have \begin{align*} \frac{f_2}{f_1}&=\frac{\sqrt{k_2}}{\sqrt{k_1}}\\\\\frac{f_2}{f_1}&=\frac{\sqrt{2\times 400}}{\sqrt{400}}\\\\ &=\sqrt{2} \end{align*} Hence, the frequency of vibrations becomes $\sqrt{2}$ times the frequency of the original spring.
Problem (8): A cork is on the surface of rippling water and does have an up-and-down motion. The cork's vertical displacement motion $y$ is described by the following function \[y(t)=3.3 \sin\left(\frac 13 t+\frac{\pi}5\right)\] All quantities are in SI units. (a) Find the amplitude, frequency, period, angular frequency, and phase constant of the motion.
(b) Where is the cork at time $t=2\,{\rm s}$.
(c) Find the velocity and acceleration of the motion as functions of time and their corresponding maximum values.
(d) Find the initial values of the position, velocity, and acceleration of the cork.
Solution: The standard equation of motion for simple harmonic motion is given by the formula $y(t)=A\sin(\omega t+\delta)$ where $A$ is the amplitude, $\omega$ is the angular frequency, and $\delta$ is the phase constant. The angular frequency is also related to the period $T$ and frequency $f$ as $\omega=2\pi f=2\pi/T$.
(a) In this problem, the given function is similar to the function of simple harmonic motion (SHM). By comparing these two functions, we can find the quantities asked for. Therefore, \begin{gather*} A=3.3\quad{\rm m} \\ \omega=\frac 13\quad{\rm rad/s} \\ T=\frac{2\pi}{\omega}=6\pi\quad{\rm s}\\ f=\frac{\omega}{2\pi}=\frac{2}{3\pi}\quad{\rm Hz}\\ \delta=\pi/5 \quad {\rm rad}\end{gather*}
(b) Setting $t=2\,{\rm s}$ gives the vertical position of the cork at any instant of time relative to the water level. \[y(t=2)=3.3 \sin\left(\frac 13 (2)+\frac{\pi}5\right)=3.17\,{\rm m}\]
(c) Velocity is the first derivative of the position function, so we have \begin{align*} v_y&=\frac{dy}{dt}=\frac{d}{dt} A\sin(\omega t+\delta)\\\\&=A\omega \cos(\omega t+\delta)\\\\&=(3.3)(1/3)\cos \left(\frac 13 t+\frac{\pi}5\right)\\\\&=(1.1\,{\rm m/s}) \cos \left(\frac 13 t+\frac{\pi}5\right)\end{align*} The acceleration is also obtained by differentiation with respect to velocity or second derivative of the position. \begin{align*} a_y&=\frac{dv_y}{dt}=\frac{d}{dt} A\omega\cos(\omega t+\delta)\\\\&=-A\omega^2 \sin(\omega t+\delta)\\\\&=-(3.3)(1/3)^2 \sin \left(\frac 13 t+\frac{\pi}5\right)\\\\&=-(0.37\,{\rm m/s^2}) \sin \left(\frac 13 t+\frac{\pi}5\right)\end{align*} Recall that the maximum value of sine or cosine functions like $A\cos(anything)$ or $A\sin(anything)$ is $A$. Therefore, the maximum values of velocity and acceleration are found as below \[v_{max}=1.1\,{\rm m/s} \quad,\quad a_{max}= 0.37\,{\rm m/s^2}\]
(d) By setting $t=0$ in the vertical displacement function $y(t)$, we can find the asked initial values. \begin{align*} y_0(t=0)&=(3.3)\sin(1/3\times 0+\pi/5)\\&=(3.3)\sin(\pi/5)\\&=1.94\,{\rm m}\\\\v_{0y}(t=0)&=(1.1)\cos(1/3\times 0+\pi/5)\\&=0.9\,{\rm m/s}\\\\a_{0y}(t=0)&=-(0.37)\sin(1/3\times 0+\pi/5)\\&=-0.22\,{\rm m/s^2}\end{align*}
Problem (9): The horizontal displacement of an object attached to a spring is described by the following equation \[x=0.5\cos (0.4t)\] where $x$ is in meters and $t$ is in seconds. Find the (a) amplitude, (b) frequency, (c) period, (d) maximum velocity, and (e) maximum acceleration.
Solution: The displacement of this object is varying as a cosine function, which is a characteristic feature of a simple harmonic motion with the standard equation $x=A\sin(\omega t)$ or $x=A\cos(\omega t)$. The angular frequency is also defined as $\omega=2\pi/T=2\pi f$ where $T$ and $f$ are the period and frequency of oscillations, respectively. By comparing the given equation with the standard form, one can find the requested quantities.
(a) The amplitude, which is defined as the maximum distance from the equilibrium position in an oscillating motion, is found as $A=0.5\,{\rm m}$.
(b) The period of the harmonic motion is the time it takes the motion to repeat itself and is obtained from the angular frequency by the following formula \[T=\frac{2\pi}{\omega}=\frac{2\pi}{0.4}=5\pi\,{\rm s}\]
(c) The frequency of harmonic motion, which is defined as the number of complete cycles in one second, is related to the angular frequency as below \[f=\frac{\omega}{2\pi}=\frac{0.4}{2\pi}=\frac{1}{5\pi}\,{\rm Hz}\] Keep in mind that the period and frequency are also related together by $f=1/T$.
(d) The maximum velocity in a simple harmonic motion is found as $v_{max}=A\omega$, thus in this case, we have \[v_{max}=(0.5)(0.4)=0.2\,{\rm m/s}\]
(e) The maximum acceleration in a simple harmonic motion is also found by the formula $a_{max}=A\omega^2$, therefore, \[a_{max}=(0.5)(0.4)^2=0.08\,{\rm m/s^2}\]
Problem (10): An object of mass 0.5 kg attached to a massless spring with spring constant k=15 N/m. It is displaced from its equilibrium by 4 cm and released.
(a) Find the total energy of the mass-spring system.
Solution: Recall that the total mechanical energy of a system consisting of a mass attached to a spring remains constant during back-and-forth oscillations.
The value of this constant is found by the formula $E=\frac 12 kA^2$, where $A$ is the amplitude of the spring.
In this example, the greatest distance from equilibrium (amplitude) is 5 cm so $A=0.4\,{\rm m}$. Therefore, the total mechanical energy of this system is \[E=\frac 12 kA^2=\frac 12 (15)(0.04)^2= 0.012\,{\rm J}\]
(b) Compute the elastic potential energy of the spring when it is located $2\,{\rm cm}$ from the releasing point.
Solution: When a spring is stretched or compressed, it stores a type of potential energy called elastic potential energy, whose formula is \[U_e=\frac{1}{2}kx^2\] Where $x$ is the amount of stretching or compression from its equilibrium point.
Here, the total displacement from the equilibrium point is $\Delta x=4-2=2\,{\rm cm}$. Thus, the elastic potential energy of spring stored at that location is \[U_e=\frac{1}{2} (15\,{\rm N/m})(0.02\,{\rm m})^2=0.003\,{\rm J}\]
(c) Compute the maximum velocity of the object.
We know that the sum of elastic potential energy $U_e$ and kinetic energy is the total mechanical energy of a mass-spring system, which is a constant value.
On the other hand, when $U_e$ is zero, the kinetic energy acquires its maximum value, so the mechanical energy remains constant. Therefore, at that point, we have \begin{align*} E&=P_e+\frac 12 mv^2\\\\0.012&=0+\frac 12 (0.5)v_{max}^2\\\\\Rightarrow v_{max}&=\sqrt{0.048}\\\\&=0.22\quad {\rm m/s}\end{align*}
(d) What is the velocity of the object when the block is placed 2 cm away from the spring?
Again, using the conservation of mechanical energy in the mass-spring system, we can find the velocity at each point of the path of the oscillation. \begin{align*} E&=P.E+K.E\\\\ E&=\frac 12 kx^2 + \frac 12 mv^2\\\\ 0.012 &=\frac 12 (15)(0.02)^2+ \frac 12 (0.5)v^2 \\\\\Rightarrow v&=\sqrt{3.6}=0.19\,{\rm m/s}\end{align*}
In the following article, you can find the exact meaning of potential energy in physics with some solved problems.
Problem (11): A block of mass 2 kg is attached to a spring with a spring constant of 500 N/m that lies horizontally on a surface. The block is pulled to a point 5 cm away from the equilibrium point. Calculate
(a) The work required to stretch the spring.
(b) the speed of the block when it passes through equilibrium.
Solution: (a) The work done for stretching or compressing a spring is stored in the form of potential energy, called elastic potential energy, in the spring.
The formula for elastic potential energy is as $U_s=\frac 12 kx^2$, where $x$ is the distance from the equilibrium point.
The equilibrium point is also defined as the point where neither the spring is stretched nor compressed. Therefore, \[U_s=\frac 12 kx^2=\frac 12 (500)(0.05)^2=0.0625\,{\rm J}\] The work done to bring the spring 5 cm to the right of equilibrium is about 0.06 joules.
(b) The conservation of mechanical energy in the case of the spring-mass system has the following form \[\frac 12 kA^2=\frac 12 kx^2+\frac 12 mv^2\] where $A$ is the maximum displacement from the equilibrium (amplitude), $x$ is the position of the object attached to the spring at any instant of time relative to the equilibrium, and $v$ is the object's velocity at that specific point.
In this problem, the velocity is asked when the object is in equilibrium, that is, when $x=0$. On the other hand, the spring initially is stretched by $5\,{\rm cm}$ and released from rest, so this value is the amplitude of the oscillations. Therefore, \begin{align*} \frac 12 kA^2&=\frac 12 kx^2+\frac 12 mv^2 \\ \\ \frac 12 (500)(0.05)^2&=\frac 12 k (0)+\frac 12 (2)v^2 \\ \\ \Rightarrow v&=0.8\quad {\rm m/s}\end{align*} Hence, when the block passing through the equilibrium position, its velocity is about $0.8\,{\rm m/s}$.
It is worth noting that, at this position, the speed of the object attached to the spring is always at its maximum.
(c) Suppose the coefficient of friction between the block and horizontal surface is $\mu_k=0.250$. Again, find the above speed at the equilibrium point.
Author: Dr. Ali Nemati
Date Published: 7/18/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
