- Home
- Physics Problems
- Problems
Solved Problems
A $\rm 100\,g$ rubber ball is thrown horizontally with a speed of $5\ \rm m/s$ toward a wall. It is initially traveling to the left. It rebounds with no loss of speed. The collision force is shown in the top graph below.
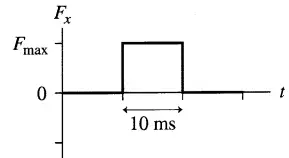
(a) What is the value of maximum force $F_{max}$?
(b) Draw an acceleration vs. time graph for the collision on the middle set of axes below. Make your graph align vertically with the force graph, and provide an appropriate numerical scale on the vertical axes.
(c) Draw a velocity vs. time graph for the collision on the bottom set of axes below. Make your graph align vertically with the acceleration graph, and provide an appropriate numerical scale on the vertical axes.
(a) If a force $F$ is applied to a particle for a time interval $\Delta t$, it causes the momentum $P$ of the particle to change. According to the original form of Newton's second law, the rate of change of the momentum of a particle is equal to the force acting on it.
In this case, since the particle rebounds back with no loss of speed, the change in its momentum is calculated as follows: \begin{align*} \Delta \vec{P} &=P_{rebound}-P_{impact} \\\\ &=m(+v)-(m(-v))\\\\ &=+2m\end{align*} (we have considered the positive direction of the coordinate to be to the right). Therefore, we have \begin{align*} F_{max}&=\frac{\Delta P}{\Delta t}\\\\ &=\frac{2mV}{\Delta t} \\\\ &=\frac{2\times 0.1\times 5}{10\times {10}^{-3}} \\\\ &=100\,\rm N \end{align*}
(b) Using Newton's second law, $a_x=F/m$, the ball has acceleration only in the time interval $10\,\rm ms$.
(c) To draw the velocity vs. time graph, use the following kinematic equation for motions with constant acceleration, $v=v_0+a\Delta t$.
In such cases, the different sections of the velocity vs. time graph are a straight line.
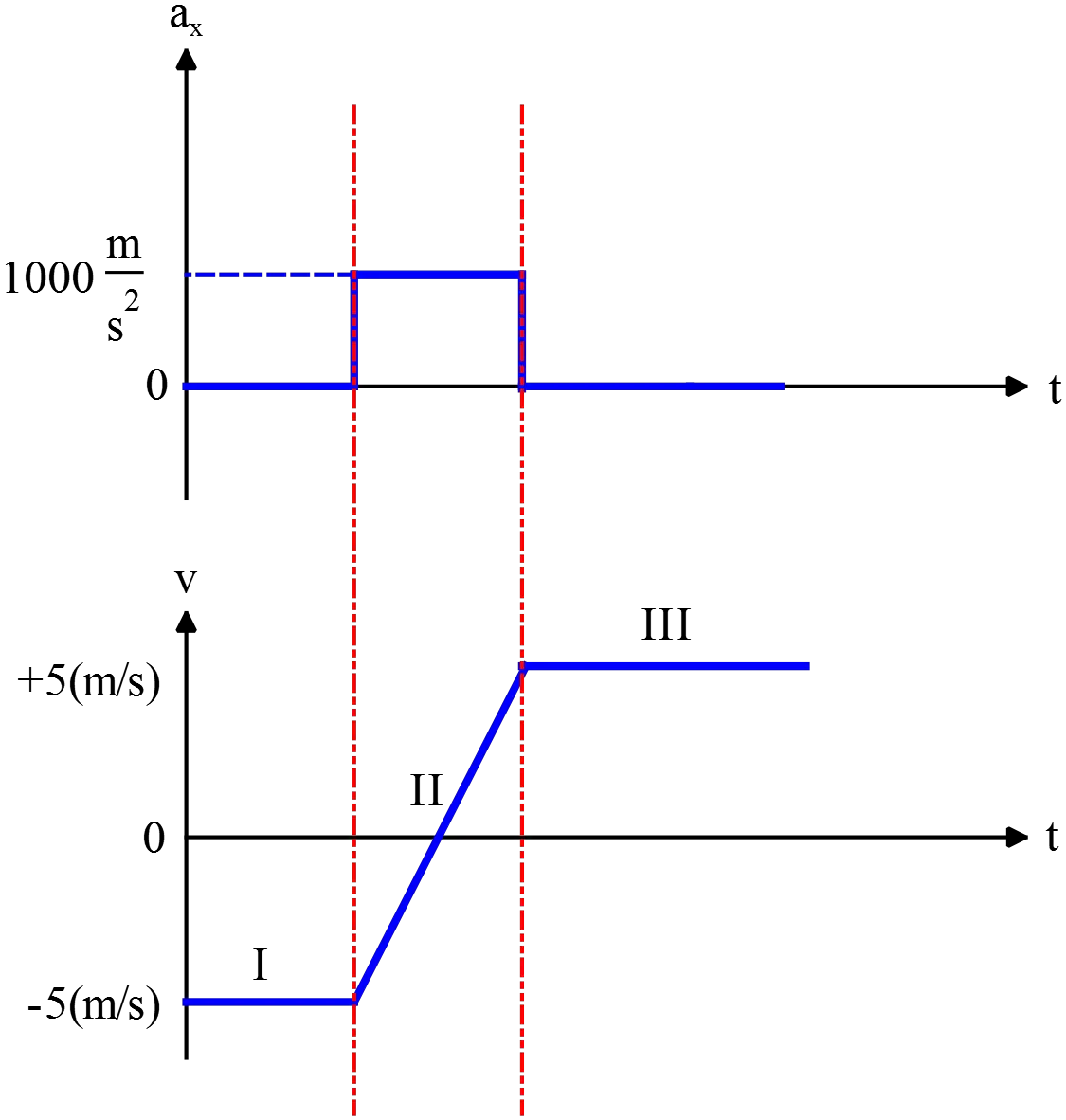
In this problem, the first section ($\rm{I}$) has$a_x=0$, so $v=v_0=-5\,\rm m/s$ which corresponds to a line parallel to the time axis.
In the second section ($\rm{II}$), $a_x=1000\,\rm m/s^2$, so \[v=v_0+a\Delta t \to v=-5+1000\,t\] Which is a diagonal line with a slope $1000$.
The third section ($\rm{III}$) is the same as the first.
A $1200\,\rm{kg}$-car moving at $15\,\rm m/s$ collides head-on with a $2000\,\rm kg$ truck initially at rest and sticks to the truck after the collision.
(a) What is their velocity just after the collision?
(b) What is the impulse on the car?
(c) If the collision lasts $0.5\,\rm s$, what is the average deceleration and force of the car?
(d) What fraction of the initial energy is lost in the collision?
(a) Since the two cars stick together after the collision, we have a completely inelastic collision. In this type of collision, the momentum of the system is conserved but the kinetic energy is not. Therefore, applying the conservation of the momentum before and after the collision, we have \begin{gather*} \vec P_i=\vec P_f \\\\ m_c{\vec{v}}_c+m_t\underbrace{{\vec{v}}_t}_{0}=\left(m_c+m_t\right){\vec{v}}_f \\\\ \Rightarrow {\vec{v}}_f=\frac{m_c}{m_c+m_t}{\vec{v}}_c \end{gather*} Substituting the given numerical values, gives \[ {\vec{v}}_f=\frac{1200}{1200+2000}\times (12)=5.63\,\rm m/s\]
(b) The impulse ($\vec{J}$) is the product of the average force and the time interval during which this force acts on an object. It is equal to the change in momentum: $\vec{J}={\vec{F}}_{ave}\Delta t=\Delta \vec{P}$. Therefore, \begin{align*} {\vec{J}}_{car}&=\Delta {\vec{P}}_{car} \\ &=m_{car}({\vec{v}}_f-{\vec{v}}_i) \\ &=1200(5.63-15) \\&=-1.13\times {10}^4\,\rm kg\cdot m/s\end{align*}
(c) By definition of the average acceleration, we have \begin{align*} {\overline{a}}_{ave}&=\frac{\Delta \vec{v}}{\Delta t} \\\\ &=\frac{v_f-v_i}{\Delta t} \\\\ &=\frac{5.63-15}{0.5} \\\\ &=-18.\,\rm m/s^2\end{align*} Now apply Newton's second law of motion to the car and find its average force \begin{align*} F_{ave}&=ma_{ave} \\ &=1200\times (-18.8) \\ &=-22.5\,\rm kN \end{align*}
(d) Find the following ratio \begin{align*} e&=\frac{K_i-K_f}{K_i} \\\\ &=\frac{\frac{1}{2}m_cv^2_c-\frac{1}{2}(m_c+m_t)v^2_f}{\frac{1}{2}m_cv^2_c} \\\\ &=\frac{1200\times {15}^2-3200\times (5.63)^2}{1200\times {15}^2} \\\\ \Rightarrow \quad e&=\boxed{0.625}\end{align*}
A 0.5 kg cart and a 2 kg car are attached and are rolling forward with a speed of 2 m/s. Suddenly a spring-loaded plunger pops out and blows the two carts apart from each other. The smaller mass cart shoots backward at $2.0\, \mathrm{m/s}$.
(a) What are the speed and direction of the $2\, {\rm kg}$ cart?
(b) If the spring constant of the plunger is $25000\, {\rm N/m}$, by how much was the spring initially compressed?
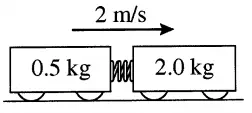
(a) There is no external force (such as friction) in the $x$ direction, so from the principle of the conservation of momentum, we have:
\begin{gather*} {\vec{P}}_i={\vec{P}}_f \\\\ (m_1+m_2){\vec{V}}_i=m_1{\vec{V}}_{1f}+m_2{\vec{V}}_{2f} \\\\ (2+0.5)(+2)=0.5\times (-2)+2V_{2f} \\\\ \Rightarrow V_{2f}=+3\,\rm m/s \end{gather*} The positive sign indicates that $2\,\rm kg$ block is moving to the right (since we have considered the positive direction to be to the right).
(b) Using the conservation of mechanical energy $E_1=E_2$, we obtain
\[\frac{1}{2}k\Delta x^2+\frac{1}{2}(m_1+m_2)V^2_i=\frac{1}{2}m_1V^2_{1f}+\frac{1}{2}m_2V^2_f\] Where $\frac{1}{2}kx^2$ represents the elastic potential energy of the spring. Therefore, solving for $\Delta x^2$, and substituting the given values, yields: \begin{gather*} \Delta x^2=\frac{1}{k}\left(m_1V^2_{1f}+m_2V^2_{2f}-\left(m_1+m_2\right)V^2_i\right) \\\\ \Delta x^2=\frac{1}{25000}\left(0.5\times {\left(-2\right)}^2+2\times 3^2-\left(2.5\right)\times 2^2\right) \\\\ \Delta x=\sqrt{\frac{10}{25000}}=\sqrt{4\times {10}^{-4}}=0.02\,\rm m\end{gather*} In the last equality, the square root of both sides is taken.
A ball of mass $0.25\,\rm kg$ is dropped vertically from a height of 1.8 m and bounces back to the original height. What is the magnitude of the impulse that the floor exerts on the ball during the bounces?
To reach the initial height, the velocity just before and after the bounce must have equal magnitude but opposite direction (because of conservation of mechanical energy).
According to the conservation of mechanical energy, the initial mechanical energy is equal to the final mechanical energy. We can express this as: \begin{gather*} E_i=E_f \\\\ \Rightarrow mgh=\frac{1}{2}mv^2\to v=\sqrt{2gh} \end{gather*}
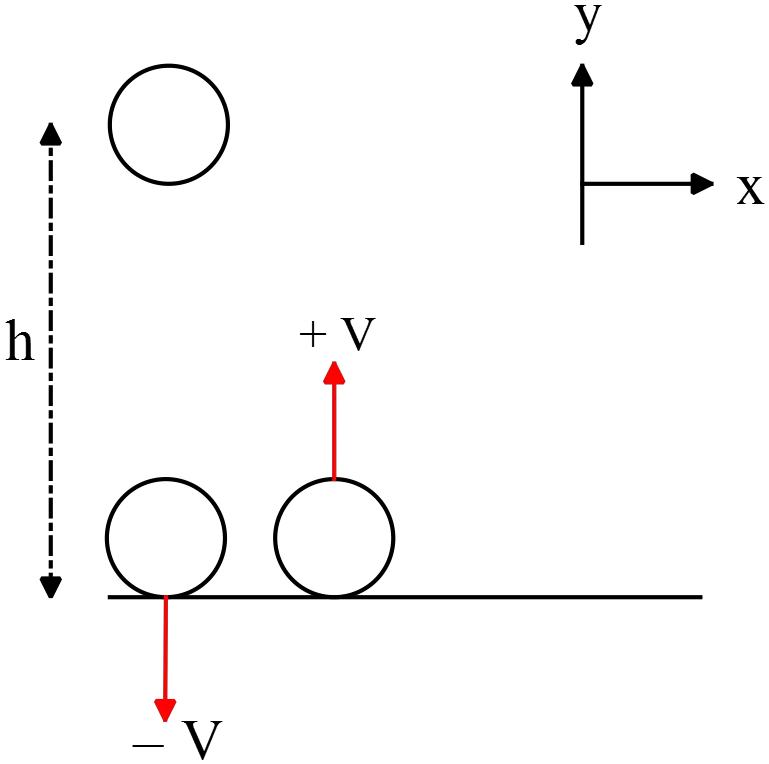
When a net force acts on an object, the impulse of this force is equal to the change in the momentum of the object that is $\Delta \vec{P}=\Delta \vec{F}\cdot \Delta t$. Substituting the numerical values into this gives \begin{align*} \Delta \vec{P}&=m({\vec{v}}_2-{\vec{v}}_1) \\\\ &=m (v\hat{j}-v(-\hat{j})) \\\\ &=2mv\ \hat{j} \end{align*} Here, ($\vec{v}_1$) represents the velocity just before the bounce, and ($\vec{v}_2$) represents the velocity just after the bounce. Substituting $\sqrt{2gh}$ for $v$ in the above equation, we get \begin{align*} \Delta P &=2m\sqrt{2gh} \\\\ &=2(0.250)\sqrt{2(9.8)(1.8)} \\\\ &=2.97\,\rm kg\cdot m/s \end{align*}
Two blocks, $M=2m$, sit on a horizontal frictionless surface with a compressed massless 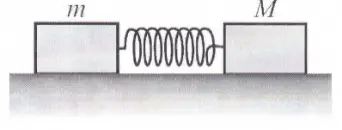 spring between them. After the spring is released $M$ has velocity $v$. What was the total energy initially stored in the spring?
spring between them. After the spring is released $M$ has velocity $v$. What was the total energy initially stored in the spring?
In this problem, releasing the spring can be viewed as an explosion, therefore momentum and mechanical energy must be conserved.
\[{\vec{P}}_{initial}={\vec{P}}_{final}\]
\[0=M\vec{v}+m{\vec{v}}_1\to v_1=-2v\]
Initially the system, due to the spring, has potential energy. After releasing the spring potential energy converts to the kinetic energy, so in final we have
\[U_{initial}=K_{final}=\frac{1}{2}Mv^2+\frac{1}{2}mv^2_1\]
\[=\frac{1}{2}\left(2m\right)v^2+\frac{1}{2}m{\left(-2v\right)}^2=3mv^2\]
\[\Rightarrow U_{initial}=3mv^2\]
A heavy wooden block rests on a flat table and a high-speed bullet is fired horizontally into the block, the bullet stopping in it.
How far will the block slide before coming to a stop?
The mass of the bullet is 10.5 g, the mass of the block is 10.5 kg, the bullet's impact speed is 750 m/s, and the coefficient of kinetic friction between the block and the table is 0.220.
We can treat this as two separate events
(i) Bullet colliding with the block: to find the speed of the block, we’ll use the conservation of momentum.
(ii) Block (and bullet) sliding with friction: To determine the distance, we’ll use the conservation of energy or the work-energy theorem.
Let’s start with the conservation of momentum. The combined speed of the block and bullet after the collision can be calculated as follows: \begin{align*} P_i&=P_f\\\\ m_{bul}\,v_{i,bul}&=(m_{bul}+M_{blo})V_f \\\\ \Rightarrow V_f&=\frac{m_{bul}}{m_{bul}+M_{blo}}v_{i,bul}\\\\&=\left(\frac{0.0105\,{\rm kg}}{0.0105+10.5}\right)750\\\\ &=0.75\quad {\rm m/s}\end{align*} where $W_f$ is the work done by the friction force. The remaining part is a kind of work-energy theorem problem. Apply this principle to find the desired distance.
\begin{align*} K_2-K_1&=W_{net} \\\\ 0-\frac{1}{2}(m_{bul}+M_{blo})V^2_f&=W_f\\\\&=-f_kd\\\\&=-{\mu }_k(m_{bul}+M_{blo})gd \\\\ \Rightarrow V_f^2 &=2{\mu }_kgd \end{align*} Solving the above equation for $d$, and substituting the numerical values, we have
\begin{align*} d&=\frac{V^2_f}{2{\mu }_kg}\\\\&=\frac{(0.75)^2}{2\times 0.22\times 9.8}\\\\&=0.13\quad {\rm m}\end{align*} Because, we want the system to come to a stop, so $K_1=0$.
In the above expressions, $W_f$ is the work done by the friction force $f_k$.
If you want to more about static and kinetic coefficient friction force, refer to the following page:
Coefficient of friction problems and solutions
In a pool game, the cue ball, which has an initial speed of $5.0\,\mathrm{m/s}$, makes an elastic collision with the eight ball, which is initially at rest. After the collision, the eight ball moves at an angle of $30{}^\circ $ to the right of the original direction of the cue ball. Assume that the balls have equal mass.
(a) Find the direction of the motion of the cue ball immediately after the collision.
(b) Find the speed of each ball immediately after the collision.
(a) An elastic collision conserves both momentum and energy:
\begin{gather*} m{\vec{V}}_i=m{\vec{V}}_8+m{\vec{V}}_c \\\\ \frac{1}{2}mV^2_i=\frac{1}{2}mV^2_8+\frac{1}{2}mV^2_c \\\\ \Rightarrow V^2_i=V^2_8+V^2_c \end{gather*} Where $\vec{V_i}$ is the initial velocity of the cue ball.
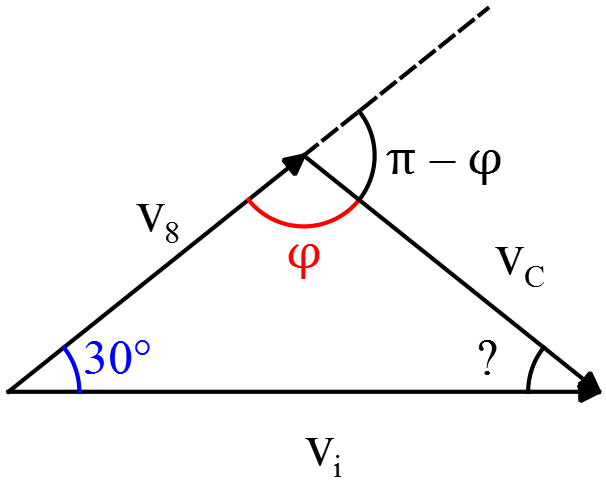
From the geometry above, we can obtain \[{\vec{V}}_i={\vec{V}}_8+{\vec{V}}_c\] Squaring both sides of the above relation and using the result of the conservation of kinetic energy, we get
\begin{gather*} {\vec{V}}^2_i=({\vec{V}}_8+{\vec{V}}_c) \cdot ({\vec{V}}_8+{\vec{V}}_c) \\\\ \Rightarrow V^2_i=V^2_8+V^2_c+2{\vec{V}}_8 \cdot {\vec{V}}_c \end{gather*} Substituting the values gives: \begin{align*} V^2_i&=V^2_8+V^2_c+2V_8V_c\,\cos (\pi -\varphi) \\\\&=\underbrace{V^2_8+V^2_c}_{V^2_i}-2V_8V_c \cos \varphi \end{align*} Equating both sides, gives \[\cos \varphi=0\] Therefore, we conclude that $\phi =90^\circ$, i.e., the angle of cue ball with respect to $\vec{V_i}$ must be $60^\circ$.
(b) Now we can use the conservation of the momentum in $x$ and $y$ directions, separately.
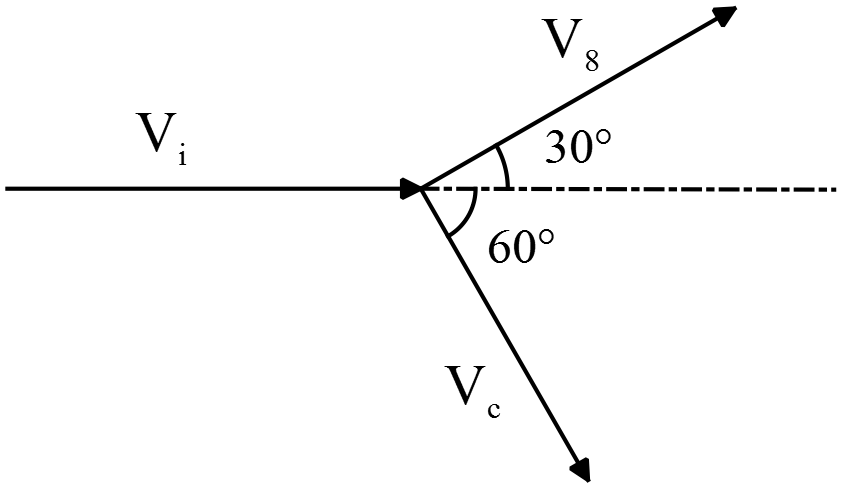
\begin{gather*} P_{ix}=mV_i \\\\ P_{fx}=m(V_8\,\cos 30^\circ+V_c\,\cos 60^\circ) \end{gather*} Equating the above momenta in the $x$-direction and solving for $V_i$, gives \begin{gather*} P_{ix}=P_{fx} \\\\ \Rightarrow V_i=V_8\,\cos 30^\circ+V_c\,\cos 60^\circ \\\\ 5=V_8\left(\frac{\sqrt{3}}{2}\right)+V_c\left(\frac{1}{2}\right)\ \ ,\ \ (*) \end{gather*} Next, write the conservation of momentum for the $y$-axis and set $P_{iy}=0$ since the cue ball moves initially only in the $x$ direction. \begin{gather*} P_{iy}=P_{fy}=V_8\,\sin 30^\circ-V_c\,\sin 60^\circ=0 \\\\ V_8\left(\frac{1}{2}\right)-V_c\left(\frac{\sqrt{3}}{2}\right)=0 \\\\ \Rightarrow \quad V_c=\frac{1}{\sqrt{3}}V_8\ \ ,\ \ (**) \end{gather*} Using (*) and (**) and solving for $V_8$, we get: \begin{gather*} 5=V_8\left(\frac{\sqrt{3}}{2}\right)+\frac{1}{\sqrt{3}}V_8\left(\frac{1}{2}\right) \\\\ \Rightarrow V_8=\frac{10}{\sqrt{3}+\frac{1}{\sqrt{3}}}=\boxed{4.33\,\rm m/s}\end{gather*}
Now by substituting $V_8$ into the relation $*$, we obtain the desired speed $V_C$
\[V_c=\frac{1}{\sqrt{3}}V_8=\frac{10}{4+1}=2.5\,\rm m/s\]
A heavy ball with a mass of $2.0\, \mathrm{kg}$ is sitting on a tabletop. A second, lighter ball is bowled toward the first ball with goal of knocking the heavy ball off the table. The light ball has a mass of $0.25\ \mathrm{kg}$.
(a) When the light ball collides with the heavy ball, it is seen that the heavy ball rolls at a speed of $1.0\ \mathrm{m/s}$ after being hit. If the collision between the two balls is elastic, then how fast was the light ball moving when it struck the heavy ball?
(b) If instead of being elastic collision, the light ball is covered with super-glue so that the two balls stick together, then how fast would the light ball need to be moving when it struck the heavy ball? The final, after collision, speed of the heavy ball is still $1.0\ \mathrm{m/s}$.
In the collision problems there are two situations:
($i$) Elastic collisions where the linear momentum and kinetic energy are conserved. And we have the following relation $v_{2f}-v_{1f}=v_{1i}-v_{2i}$
($ii$) Inelastic collisions where the linear momentum is conserved but the kinetic energy due to the internal friction is not conserved. In this collision the objects has the same velocity after the collision.
(a) We expect that the lighter ball will rebound to the left after striking heavier ball. Use 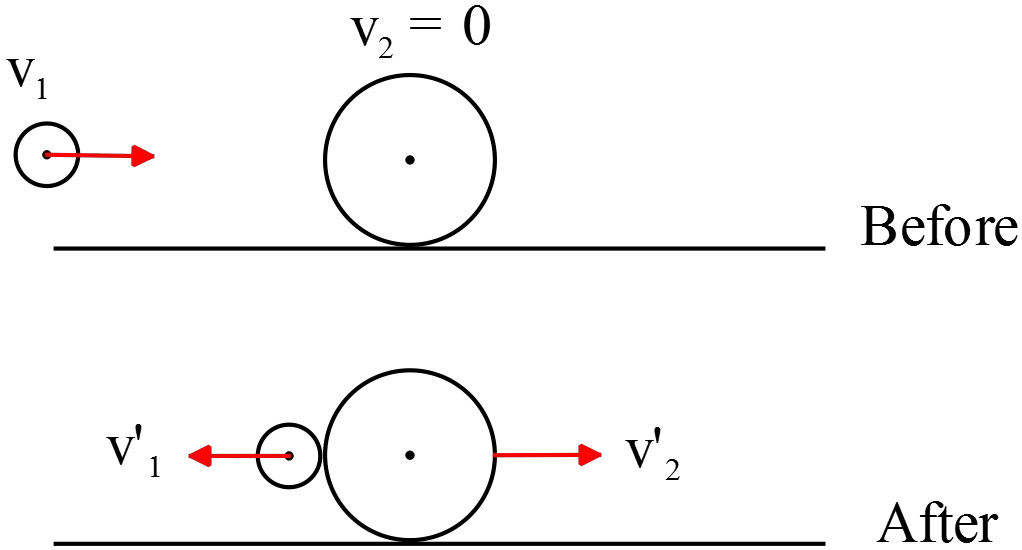 the conservation of momentum $\vec P_i=\vec P_f$ to find a relation between velocities
the conservation of momentum $\vec P_i=\vec P_f$ to find a relation between velocities
\[m_1v_1+m_2v_2=m_1v^{'}_1+m_2v^{'}_2\]
\[0.25v_1+0=0.25v^{'}_1+2\left(1\right)\Rightarrow v^{'}_1=v_1-8\ ,\ \ \left(1\right)\]
Using the general relation between relative velocities of the objects in an elastic collision, we get
\[v^{'}_2-v^{'}_1=v_1-v_2\Rightarrow 1-v^{'}_1=v_1\ ,\ \ (2)\]
\[\left\{ \begin{array}{rcl}
v^{'}_1 &=& v_1-8\ \\
1-v^{'}_1 & = &v_1 \end{array}
\right.\Rightarrow \ v_1-8=1-v_1\Rightarrow 2v_1=9\Rightarrow v_1=+4.5\ \mathrm{m/s}\]
(b) Because the two balls stick together and have the same velocity after the collision so this is an inelastic collision.
\[m_1v_1+m_2v_2=\left(m_1+m_2\right)v^{'}\]
\[0.25v_1+0=\left(0.25+2.0\right)\left(1.0\right)\Rightarrow 0.25v_1=2.25\]
\[v_1=9.0\ \mathrm{m/s}\]
Two cars, one a compact car with mass of $1200\,{\rm kg}$ and the other a large pickup truck with mass $3000\, {\rm kg}$, collide head-on at a typical freeway speeds ($70\, {\rm mph}$). The collision is inelastic and two vehicles stuck together after the collision.
(a) What is the speed of the vehicles after the collision?
(b) What are the changes of velocity for the compact car and for the truck?
(c) Which vehicle has a greater change in linear momentum?
(a) Because after the collision, the two cars stuck together, the collision is inelastic and only the linear momentum of the system is conserved.
\begin{gather*} \vec{P}_i=\vec{P}_f \\ \Rightarrow m_pv_p+m_c(-v_c)=(m_p+m_c)V \\\\ \to V=\frac{m_p-m_c}{m_p+m_c}v_i \end{gather*} By substituting the numerical values into it, we get \[V=\frac{(3000-1200)}{3000+1200}\times 70=+30\,\rm mph\]
Note: the two cars before the collision have the same velocity but in opposite directions to each other.
We assume that the pickup moves in the $+x$ and the compact in the $-x$ direction. We see that after the collision the common final velocity of the two cars is positive namely, the cars are moving in the $+x$ direction.
(b) The change in the velocity of pickup is found as below \begin{align*} \Delta v_p&=(v_p)_{after}-(v_p)_{before} \\ &=30-70 \\ &=-40\quad\rm mph \end{align*} And similarly, the change in the compact's velocity is \begin{align*} \Delta v_c&=(v_c)_{after}-(v_c)_{before} \\ &=+30-(-70) \\ &=+100\quad\rm mph\end{align*}
(c) The changes in the momentum $\Delta P=m\Delta v$ is determined as below \begin{gather*} \Delta P_c=m_c\Delta v_c=1200\,(+100)=12\times {10}^4\,{\rm kg\cdot mph} \\ \Delta P_p=m_p\Delta v_p=3000\,(-40)=-12\times {10}^4\,{\rm kg \cdot mph} \end{gather*} Therefore, the changes in the momentum are the same but in the opposite directions.
A bullet of mass $m=0.01\, \rm {kg}$ is fired at a wooden block of mass $M=1.00\,\rm{kg}$ as shown. The velocity of the bullet just before it strikes the block is 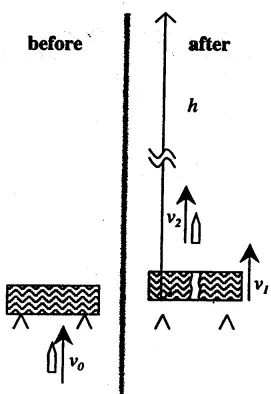 $v_0=850\,\rm m/s$.
$v_0=850\,\rm m/s$.
The bullet passes through the block and rises to a maximum height $h=1200\,\rm{m}$.
(a) What is the velocity $v_2$ of the bullet just after it exits the blocks?
(b) What is the $v_1$ velocity of the block just after the bullet has left it?
(c) What is the kinetic energy that is lost in the collision?
(d) The bullet passes through the block in $3\times {10}^{-5}\,\mathrm{s}$. What is the average force (magnitude and direction) that the block exerts on the bullet?
(a) Use the conservation of energy just after the bullet exits the block at the speed of $v_2$ and when it reaches the height $h$. That is, $E_i=E_f$
\begin{gather*} E_i=E_f \\\\ \frac{1}{2}mv^2_2=mgh \end{gather*} Solving the above equation for $v_2$ and substituting the given values, we obtain \begin{align*} v_2&=\sqrt{2gh}\\\\&=\sqrt{2\times 9.8\times 1200}\\\\&=153.36\,\rm m/s \end{align*}
(b) Apply the conservation of the momentum during the collision as \begin{gather*} P_i=P_f \\\\ mv_0=Mv_1+mv_2 \end{gather*} Solving for $v_1$ and plugging in the given numerical values yields: \begin{align*} v_1&=\frac{m}{M}(v_0-v_2)\\\\ &=\frac{0.01}{1}(850-153.36) \\\\ &=6.96\,\rm m/s \end{align*}
(c) To find the amount of kinetic energy lost during this inelastic collision, subtract the kinetic energies of the bullet and the block from the initial kinetic energy as follows: \begin{align*} \Delta K&=\frac{1}{2}mv^2_0-\left(\frac{1}{2}Mv^2_1+\frac{1}{2}mv^2_2\right) \\\\ &=3470\,\rm J\end{align*} Since $\Delta K\neq 0$, this is an inelastic collision, as expected.
(d) When a net average force $\Sigma \vec{F}$ acts on an object during a time interval $\Delta t$, the impulse-momentum theorem states that the impulse of this force equals the change in the momentum of that object, i.e., \[\Sigma \vec{F}\cdot t=\Delta P=m{\vec{v}}_f-m{\vec{v}}_i\] Therefore, substituting the values into this gives: \begin{align*} \Sigma \vec{F}&=\frac{\Delta \vec P}{\Delta t} \\\\ &=\frac{m(v_2-v_0)}{\Delta t} \\\\ &=\frac{(0.01)(153.36-850)}{3\times 10^{-5}} \\\\ &=-2.32\times {10}^5\,\rm N \end{align*} The negative sign indicates that the net force is in the opposite direction of the motion of the bullet (downward).
A 24 g bullet is shot vertically into a 3 kg block. The block lifts upward 8.00 mm. The bullet penetrates the block and comes to rest in it in a time interval of 0.001 s. Assume the force on the bullet is constant during penetration and that air resistance is negligible. What is the initial kinetic energy of the bullet?
Let $v_0$ be the initial velocity, $v_1$ be the velocity of the bullet and block after penetration.
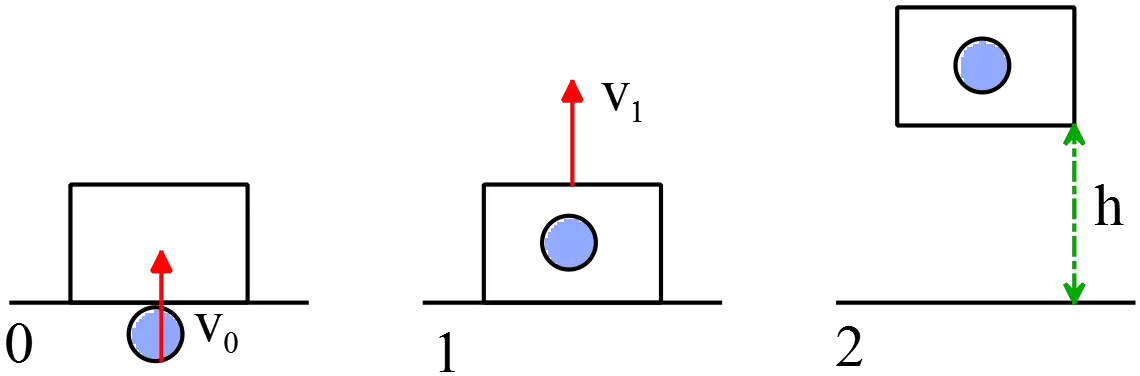
First, use the conservation of mechanical energy after collision and at the instant that the system reaches the height $8\, \rm{mm}$ to find $v_1$ as
\begin{align*} E_1&=E_2 \\\\ \frac{1}{2}(m+M)v^2_1&=(m+M)gh\\\\ \Rightarrow \quad v_1&=\sqrt{2gh}\\\\&=\sqrt{2\times 9.8\times 0.008}\\\\& =0.396\quad {\rm m/s}\end{align*}
Now use the linear momentum conservation just before and just after the collision. Since the bullet and block have the same velocity immediately after the collision, this case is an inelastic collision.
\begin{align*} P_0&=P_1\\\\ mv_0&=(m+M)v_1\\\\ \Rightarrow \quad v_0&=\left(1+\frac{M}{m}\right)v_1 \\\\ &=\left(1+\frac{3}{0.024}\right)(0.396) \\\\&=49.9\quad {\rm m/s} \end{align*} Therefore, the initial kinetic energy of the bullet is \begin{align*} K_0&=\frac{1}{2}mv^2_0\\\\&=\frac{1}{2}(0.024)(49.9)^2\\\\&=29.88\quad {\rm J}\end{align*}
To better understand momentum conservation, refer to the solved problems of momentum problems.
During a collision with a wall, the velocity of a $0.2\, \mathrm{kg}$ ball changes from $20\, \mathrm{m/s}$ toward the wall to $12\, \mathrm{m/s}$ away from the wall. If the time the ball was in contact with the wall was $60\, \mathrm{ms}$, what was the magnitude of the average force applied to the ball?
The average force acting on an object equals the time rate of change of its linear momentum,i.e., ${\vec{F}}_{ave}=\frac{\Delta \vec{P}}{\Delta t}$ (the original version of Newton's 2nd law), therefore \begin{align*} \Delta \vec{P}&={\vec{P}}_f-{\vec{P}}_i\\\\ &=(0.2)(12(-\hat{i})-20\hat{i}) \\\\ &=-6.4\,\rm kg\cdot m/s \ (\hat{i})\end{align*} Therefore, the average force applied to the ball upon impacting to the wall is calculated as follows: \begin{align*} {\vec{F}}_{ave}&=\frac{6.4}{60\times {10}^{-3}}(-\hat{i}) \\\\ &=106.6\,\rm N\ (-\hat{i})\end{align*} Note: the product of average force and the time interval during which this force is exerted on the body is called the impulse of this force. \[\vec{J}={\vec{F}}_{ave}=\Delta \vec{P}\]
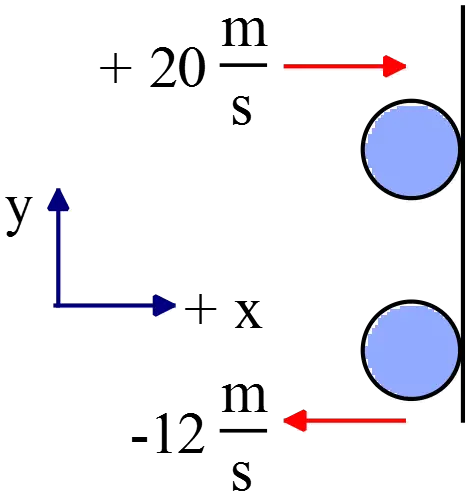
Captain Kirk is located $124\ \mathrm{m}$ from the Starship Enterprise and at rest with respect to the Enterprise. Unfortunately, Kirk's $36.6\ \mathrm{kg}$ jetpack has malfunctioned. Kirk in his spacesuit has a mass of $366\ \mathrm{kg}$. The only way for the Kirk to get back to the enterprise is to throw his jetpack out in the opposite direction of the Enterprise. Kirk is able to throw this jetpack away from him at $1.55\ \mathrm{m/s}$. How long (in minutes) will it take Captain Kirk to get back to the Enterprise?
First using the conservation of linear momentum find the velocity of the Kirk then use the kinematical relations to determine the desired time.
Since Kirk and jetpack initially are at rest so $P_i=0$, so
\[{\vec{P}}_i={\vec{P}}_f\Rightarrow 0=m_K{\vec{v}}_K+m_j{\vec{v}}_j\Rightarrow \ {\vec{v}}_K=-\frac{m_j}{m_K}{\vec{v}}_j=-\frac{36.6}{366}\left(-1.55\right)=+0.155\ \frac{\mathrm{m}}{\mathrm{s}}\]
We have chosen the positive direction to be $+x$ direction. So Kirk with the constant velocity of $0.155\ \mathrm{m/s\ }$ in direction of the Enterprise moves towards it. Thus, use the definition of the velocity to find the elapsed time.
\[x=x_0+v_0t\Rightarrow t=\frac{124}{0.155}=800s\]
Convert to minutes as $800\ \mathrm{s\times }\left(\frac{\mathrm{1min}}{\mathrm{60\ s}}\right)=13.3\ \mathrm{min}$
A cannon of mass $M=500\ \mathrm{kg}$, fixed to the ground, shoots a cannon ball of mass $m=20\ \mathrm{kg}$ at a speed of $1000\ \mathrm{m/s}$. Now the stops holding the cannon to the ground are removed, so that it is free to move. The same charge of gunpowder is used and an identical ball fired. What is the speed of the ball?
First find the energy of the gunpowder that is released and goes into the motion of the ball.
\[Q=\frac{1}{2}mv^2_0=\frac{1}{2}\left(20\right){\left({10}^3\right)}^2={10}^7\ \mathrm{J}\]
this energy causes the motion of the ball and cannon (conservation of energy!) so $Q=\frac{1}{2}Mv^2_c+\frac{1}{2}mv^2_b$. Now use the conservation of the momentum to calculate the speed of the cannon after firing then substitute it into the $Q$ relation.
\[{\vec{P}}_i={\vec{P}}_f\Rightarrow 0=M{\vec{v}}_c+m{\vec{v}}_b\Rightarrow {\vec{v}}_c=-\frac{m}{M}{\vec{v}}_b\]
\[\Rightarrow \ {\vec{v}}_c=-\frac{20}{500}\left(1000\right)=-40\ \mathrm{m/s}\]
The negative means that the cannon moves in opposite direction of the ball. Therefore,
\[Q=\frac{1}{2}Mv^2_c+\frac{1}{2}mv^2_b\Rightarrow v_b=\sqrt{\frac{2Q-Mv^2_c}{m}}=\sqrt{\frac{2\times {10}^7-500\times {\left(-40\right)}^2}{20}}=979.79\ \frac{\mathrm{m}}{\mathrm{s}}\]
A lead bullet of mass $m=10.0\ \mathrm{g}$ is traveling with a velocity of $v_0=100\ \mathrm{m/s}$ when it strikes a wooden block. The block has a mass of $M=1.00\ \mathrm{kg}$ and is at rest on the table, as shown in the diagram below. The bullet embeds itself in the block and after the impact, they slide together. All the kinetic energy that is lost in the collision is converted into heat. Assume that all this heat goes into heating up the bullet.
(a) What is the speed of the wooden block after the collision?
(b) How much heat is generated as a result of the collision?
(c) By how many degrees does the temperature of the bullet rise after the collision? (The specific heat of the bullet is $128\ \mathrm{J/(kg.{}^\circ\!{C}})$.)
(d) Suppose that the table has a coefficient of kinetic friction of $\mu=0.2$. At what distance will the block stop?
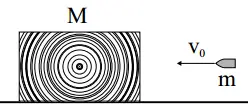
(a) Because the bullet and block stick together and have the same velocity after the collision, we have an inelastic collision. Use the conservation of momentum to find this velocity \begin{gather*} P_i=P_f \\\\ mv_0=(m+M)v_f \\\\ \Rightarrow v_f=\frac{m}{m+M}v_0 \end{gather*} Substituting the values into the equation above gives \[v_f=\frac{0.010}{0.010+1}(100)=1\,\rm m/s\]
(b) In an inelastic collision, the kinetic energy is not conserved, but the change in kinetic energy equals the heat generated during this collision, i.e., $\Delta K=-Q$. Therefore, \begin{align*} -Q&=K_f-K_i\\\\ &=\frac{1}{2}(m+M)v^2_f-\frac{1}{2}mv^2_0 \\\\ &=\frac{1}{2}(0.01+1)(1)^2-\frac{1}{2}(0.01)(100)^2 \end{align*} Hence, as a result of collision, the following amount of heat is generated. \[Q=49.495\,\rm J\] The negative sign indicates that the heat is transferred into the surroundings.
(c) The heat produced during this collision causes the temperature of the bullet to increase. Thus, using the equation $Q=mc\Delta T$ and solving for $\Delta T$, we have \begin{align*} \Delta T&=\frac{Q}{mC}\\\\ &=\frac{49.495}{(0.010)(128)} \\\\ &=38.66\,\rm ^\circ C\end{align*}
(d) Use the work-energy theorem as $K_2-K_1=W_{net}$. In this case, only the friction force does work on the system so
\begin{gather*} K_2-K_1=-W_f \\\\ 0-\frac{1}{2}(m+M)v^2_1=-\underbrace{{\mu }_k(m+M)g}_{f_k}d \end{gather*} Solving the above expression for $d$, we get \begin{align*} d&=\frac{v^2_1}{2({\mu }_k g)} \\\\ &=\frac{1^2}{2\times 0.2\times 9.8} \\\\ &=25.51\,\rm cm \end{align*}
A hockey puck of mass $m=0.35\ \mathrm{kg}$ is sliding without friction on ice, with a velocity of $8.0\ \mathrm{m/s}$ in the $x$ direction. A hockey player hits the puck with his stick, applying a constant force for $0.1\ \mathrm{s}$. As a result of this force, the puck changes direction and subsequently moves off with a velocity of $15.0\ \mathrm{m/s}$ entirely in the $y$ direction.
(a) What are the $x$ and $y$ components of the force?
(b) Give the magnitude of the force and the angle it makes relative to the positive $x$ axis.
(a) The initial and final momentums of the puck are
\[p_{ix}=mv_{ix}\ ,\ \ p_{iy}=0\ \ ,\ \ p_{fy}=mv_{fy}\ ,\ \ p_{fx}=0\]
One of the consequences of the Newton's 2${}^{nd}$ law is that the time rate of the change of particle's momentum equals the net force acting on it that is $\vec{F}=\frac{\mathrm{\Delta }\vec{P}}{\mathrm{\Delta }t}$. So
\[F_x=\frac{\mathrm{\Delta }P_x}{\mathrm{\Delta }t}=\frac{P_{fx}-P_{ix}}{\mathrm{\Delta }t}=\frac{0-mv_{ix}}{\mathrm{\Delta }t}=-\frac{8\times 0.35}{0.1}=-28\ \mathrm{N}\]
\[F_y=\frac{\mathrm{\Delta }P_y}{\mathrm{\Delta }t}=\frac{P_{fy}-P_{iy}}{\mathrm{\Delta }t}=\frac{mv_{fy}-0}{\mathrm{\Delta }t}=\frac{0.35\times 15}{0.1}=52.5\ \mathrm{N}\]
(b) Recall that if the components of a vector are given, its magnitude and direction w.r.t horizontal axis are determined by
\[\left|\vec{F}\right|=\sqrt{F^2_x+F^2_y}=\sqrt{{\left(-28\right)}^2+{\left(52.5\right)}^2}=59.5\ \mathrm{N}\] 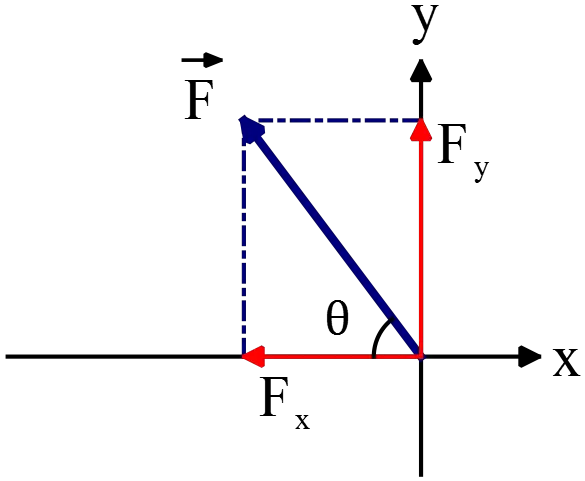
\[\theta ={\tan^{-1} \left(\frac{\left|F_y\right|}{\left|F_x\right|}\right)\ }={\tan^{-1} \left(\frac{52.5}{28}\right)\ }=61.9{}^\circ \]
Since $x$ component is negative and $y$ component is positive so the resultant vector lies in the second quadrant.
A $0.05\ \mathrm{kg}$ hockey puck (labeled $m_2$) is at rest in the center of an air hockey table when a smaller puck with mass $m_1=0.025\ \mathrm{kg}$ moving with velocity $v_{i1}=5\ \mathrm{m/s\ }$collides with it. After collision the pucks move off as shown in the picture.
(a) What is the velocity of each puck after the collision?
(b) Is this collision elastic?
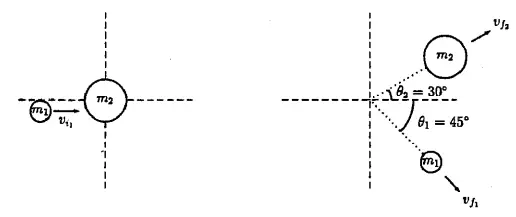
(a) Use the conservation of the momentum in the $x$ and $y$ directions:
\[P_{ix}=P_{fx}\Rightarrow m_1{\left(v_{1i}\right)}_x+m_2{\left(v_{2i}\right)}_x=m_1{\left(v_{1f}\right)}_x+m_2{\left({\vec{v}}_{2f}\right)}_x\]
\[\Rightarrow m_1v_{1i}=m_1v_{1f}\,{\cos 45{}^\circ \ }+m_2v_{2f}\,{\cos 30{}^\circ \ }\ \ ,\ \ \mathrm{(I)}\]
\[P_{iy}=P_{fy}\Rightarrow 0=m_1{\left(v_{1f}\right)}_y+m_2{\left(v_{2f}\right)}_y\]
\[\Rightarrow -m_1v_{1f}\,{\sin 45{}^\circ \ }+m_2v_{2f}\,{\sin 30{}^\circ \ }=0\ \ ,\ \ \mathrm{(II)}\]
From $\mathrm{(II)}$ we get
\[v_{2f}=\frac{m_1v_{1f}\,{\sin 45{}^\circ \ }}{m_2\,{\sin 30{}^\circ \ }}\]
Insert $v_{2f}$into $\mathrm{(I)}$, we obtain
\[m_1v_{1i}=m_1v_{1f}\,{\cos 45{}^\circ \ }+m_2\left(\frac{m_1v_{1f}\,{\sin 45{}^\circ \ }}{m_2\,{\sin 30{}^\circ \ }}\right){\cos 30{}^\circ \ }\]
\[v_{1i}=v_{1f}\left({\cos 45{}^\circ \ }+{\sin 45{}^\circ \ }{\cot 30{}^\circ \ }\right)\]
\[\Rightarrow v_{1f}=\frac{v_{1i}}{\left({\cos 45{}^\circ \ }+{\sin 45{}^\circ \ }{\cot 30{}^\circ \ }\right)}=2.6\ \frac{\mathrm{m}}{\mathrm{s}}\]
\[v_{2f}=\frac{m_1v_{1f}\,{\sin 45{}^\circ \ }}{m_2\,{\sin 30{}^\circ \ }}=1.8\ \frac{\mathrm{m}}{\mathrm{s}}\]
(b) To see that whether the collision is elastic or inelastic, we must calculate the initial and final kinetic energy of the pucks before and after the collision.
\[K_i=K_{1i}+K_{2i}=\frac{1}{2}m_1v^2_{1i}+0=0.31\ \mathrm{J}\]
\[K_f=K_{1f}+K_{2f}=\frac{1}{2}m_1v^2_{1f}+\frac{1}{2}m_2v^2_{2f}=0.17\ \mathrm{J}\]
Since during this collision some of the kinetic energy lost as a heat into the surrounding so we have an inelastic collision.
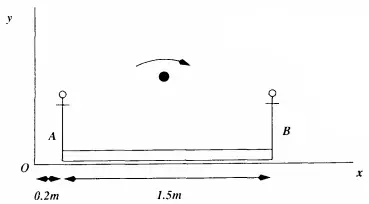
Two equal mass people are symmetrically located at the extreme ends of a uniform $1.5\ \mathrm{m}$ long platform. The combined mass of the people and platform is $150\ \mathrm{kg}$. Additionally one person holds a $6\ \mathrm{kg}$ ball at end $A$ of the platform. The platform sits on a frictionless surface.
(a) What is the $x$ coordinates of the center of the mass of the system.
The person on end A now throws the ball to the other person who catches it right at the opposite end of the platform.
(b) Does the center of mass of the whole system change location?
(c) After the ball is caught, what is the $x$ coordinate of end A of the platform?
(a) By definition, the center of mass of a collection of point particles is
\[{\vec{r}}_{cm}=\frac{\Sigma m_i{\vec{r}}_i}{M}\]
Let the mass of ball be $m_b$. Therefore
\[x_{cm}=\frac{(m_Ax_A+m_Bx_B)+m_br_b}{M+m_b}=\frac{150\left(0.95\right)+6\times 0.2}{150+6}=0.92\ \mathrm{m}\]
Since the combined mass of the people and platform is given, we must consider it as a new mass $M$ located at the center of the platform $0.95\mathrm{m}$ away from the axis.
(b) Since there are no frictional forces act on the system (external forces) so due to Newton's 2${}^{nd}$ law the center of the mass does not change.
(c) After the ball is caught by the B, all points of the system moving to the left by amount of $x$. So first, calculate the new center of mass and then set it to the previous magnitude! (see figure below)
\[x^{'}_{cm}=\frac{150\left(0.95-x\right)+6\left(1.7-x\right)}{150+6}\]
\[x^{'}_{cm}=x_{cm}=0.92\Rightarrow x=0.14\ \mathrm{m}\]
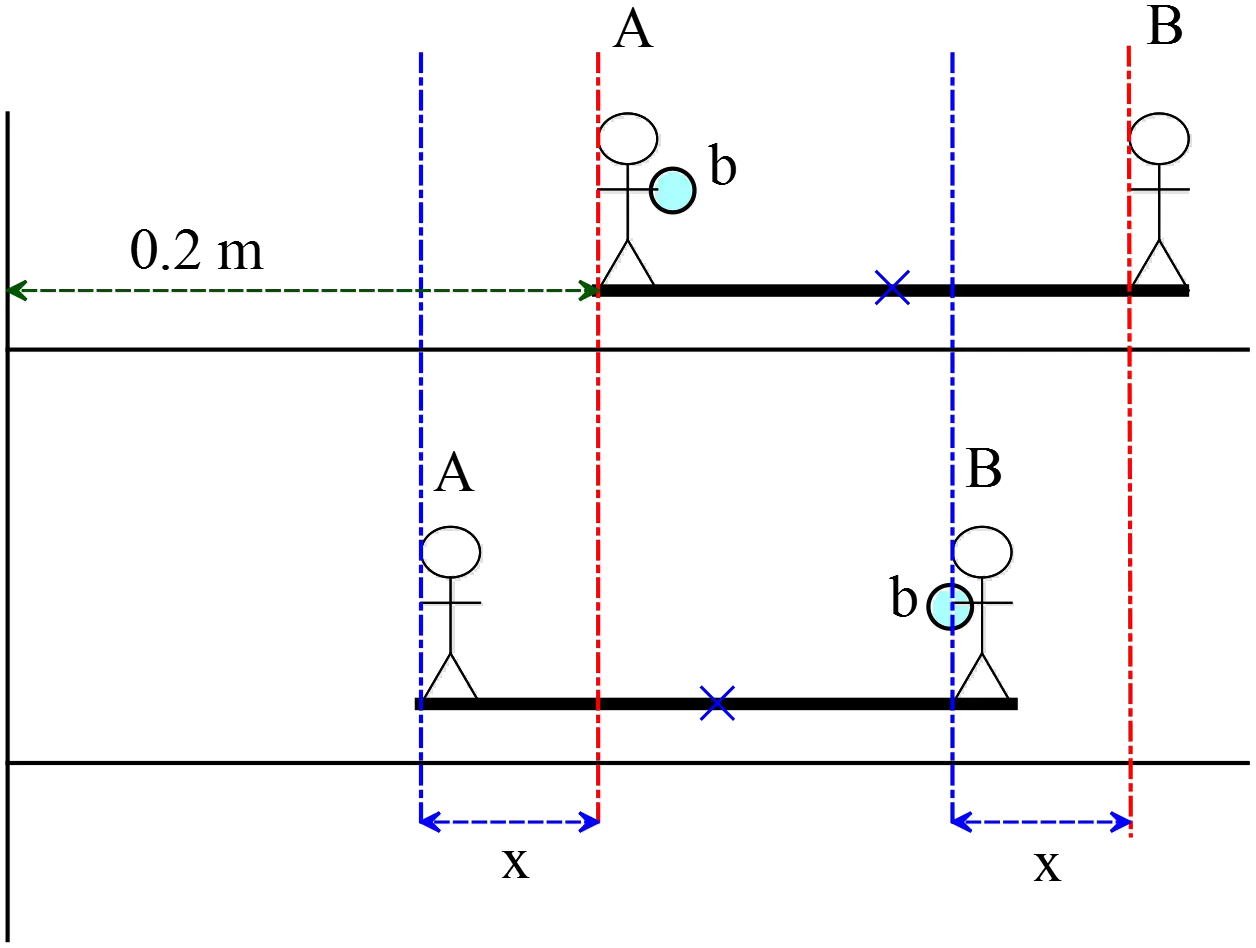
A man of mass $M=60\ {\rm kg}$ stands in the center of a platform one of mass $m=40\ {\rm kg}$ that rests on ice. Another identical platform floats at a distance $L=1.5\ {\rm m}$ away. The contact of the two platforms with the ice is frictionless. The man jumps from the first to the second platform, and lands in the center of the second platform.
(a) Locate the center of mass of the two-platform and man system before the man jumps. Use the center of mass of platform one as origin.
(b) What is the velocity $v_{CM}$of the center of mass of the two-platform and man system when the man is midway between the two platforms?
(c) How far apart are the two platforms when the man lands?
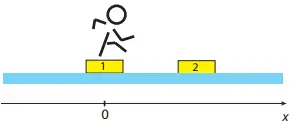
(a) Using the definition of the center of mass of a system of masses $m_i$ at distances $r_i$ from the origin, we get
\[x_{cm}=\frac{\Sigma m_ir_i}{\Sigma m_i}=\frac{\left(m+M\right)x_1+mx_2}{m+M+m}=\frac{\left(60+40\right)\left(0\right)+(40\times 1.5)}{40+60+40}=0.43\ \mathrm{m}\]
Away from the origin.
(b) Since there is no external force acting on the two-platform and man system, Newton's second law $\Sigma {\vec{F}}_{ext}=M\frac{d}{dt}{\vec{v}}_{cm}$states that the velocity of the center of mass is constant over time or is conserved. The initial velocity of cm is zero so its final velocity must be also zero.
\[{\left(v_{cm}\right)}_i={\left(v_{cm}\right)}_f=0\]
(b) Similar to the reasoning above, since there is no external force, the cm does not move that is ${\left(x_{cm}\right)}_i={\left(x_{cm}\right)}_f=0.43\ \mathrm{m}$
Let us denote the final position of the platforms by $x^{'}_1$ and $x^{'}_2$. At the moment the man lands on the platform two, the position of this platform has not changed yet so
\[{\left(x_{cm}\right)}_f=\frac{\left(m+M\right)x^{'}_2+mx^{'}_1}{2m+M}\]
\[=\frac{\left(m+M\right)x^{'}_2+m\left(-\mathrm{\Delta }x\right)}{2m+M}={\left(x_{cm}\right)}_i=0.43\]
Solving for $\mathrm{\Delta }x$ (shown in the figure), we get
\[\Rightarrow \frac{\left(40+60\right)\left(1.5\right)-40\mathrm{\Delta }x}{2\left(40\right)+60}=0.43\]
\[\mathrm{\Delta }x=2.245\ \mathrm{cm}\]
This is the distance of platform one from the origin at the moment the man lands on the second platform. From the figure, we can find the distance between the platforms as
\[d=\mathrm{\Delta }x+1.5=3.745\ \mathrm{m}\]
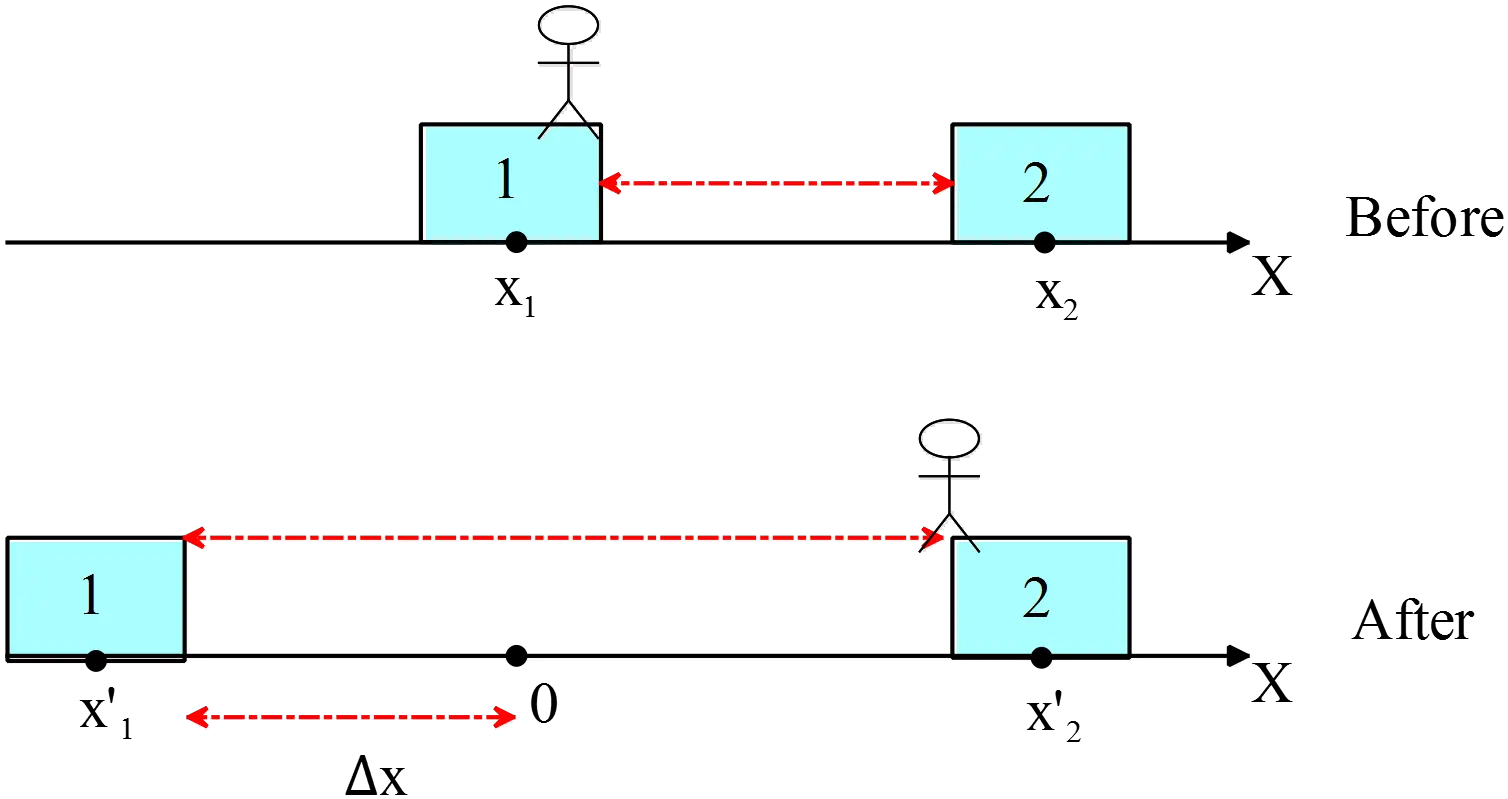
An 8 g bullet is shot into a 4 kg block, at rest on a frictionless surface. The bullet remains lodged in the block. The block moves into spring and compresses it by 3 cm. The force constant of the spring is $1500\, {\rm N/m}$.
(a) What is the initial velocity of the bullet?
(b) What is the impulse, due to the spring, during the entire time interval in which block and spring are in contacts?
(a) Apply the conservation of linear momentum between entering and lodging the bullet in the block ($2$)
\[P_1=P_2\Rightarrow mV_0=\left(M+m\right)V_2\]
Now apply the conservation of mechanical energy between the instant of entering the bullet into the block ($2$) and after the bullet + block come to a stop ($3$)($K_f=0$)
\[E_2=E_3\Rightarrow \frac{1}{2}\left(m+M\right)V^2_2=\frac{1}{2}kx^2\]
By combining these two relation, we obtain the initial velocity of the bullet
\begin{align*} \frac{1}{2}(m+M)\left(\frac{m}{m+M}\right)^2V^2 &=\frac{1}{2}kx^2\\\\ \Rightarrow \quad V&=\frac{L}{m}\sqrt{k(m+M)}\\\\ &=\frac{0.03}{0.008}\sqrt{1500(0.008+4)}\\\\&=290.76\quad {\rm m/s}\end{align*} where in above we set $x=L$.
(b) Impulse is defined by the following relation
\[\vec{J}=\underbrace{\vec{F}\cdot\mathrm{\Delta }t}_{impulse}=\mathrm{\Delta }\vec{P}\]
So we must find the change in momentum of the block + bullet during the time interval stated above. Block+bullet after coming to a stop, start again move in the opposite direction (the elastic potential energy at the end of the path convert to the kinetic energy) Since there is no friction then there is an asymmetry between going and backing paths. Therefore, we must multiply the going result by two to find the total time in which the block+bullet is in contact.
\begin{align*} J_{2\to 3}&=(m+M)(\underbrace{V_3}_{0}-V_2)\\\\&=(m+M)\left(0-\frac{m}{m+M}V\right) \\\\&=-mV\\\\ &=-0.008\times 290.76=2.32\,{\rm N.m}\end{align*} Therefore, the total momentum is \[J_{tot}=J_{2\to 3}+J_{3\to 2}=4.65\quad {\rm N.s}\]
You can find more solved problems on impulse and momentum, here.
MOST USEFUL FORMULA IN MOMENTUM AND COLLISION:
Momentum of a particle:
\[\vec p=m\vec v\]
Newton's second law :
\[\Sigma \vec F=\frac{d\vec p}{dt}\]
Kinetic energy of a particle:
\[K=\frac 1 2 mv^2\]
Impulse:
\[\vec J=\Sigma \vec F \left(t_2-t_1\right)\]
Impulse-Momentum theorem:
\[\vec J_{net}=\Sigma \vec F_{net} \Delta t=\Delta P\]
Relative speeds of approach and separation in elastic collision:
\[v_{2f}-v_{1f}=v_{1i}-v_{2i}\]
Center of mass:
\[\vec r_{cm}=\frac {\Sigma m_i \vec r_i}{\Sigma m_i}=\frac{m_1\vec r_1+m_2\vec r_2+\cdots}{m_1+m_2+\cdots}\]
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
