Coulomb's Law: Solved Problems for High School and College
Practice problems with detailed solutions about Coulomb's law are presented that are suitable for the AP Physics C exam and college students. For more solved problems (over 61) see here.
Note: In textbooks, the terms ‘Coulomb force’, ‘electric force’, and ‘electrostatic force’ are used interchangeably to describe the force between two point charges.
Coulomb's Law Practice Problems
Problem (1): Two like and equal charges are at a distance of $d=5\,{\rm cm}$ and exert a force of $F=9\times 10^{-3}\,{\rm N}$ on each other.
(a) Find the magnitude of each charge.
(b) What is the direction of the electrostatic force between them?
Solution: The magnitude of the force between two rest point charges $q$ and $q'$ separated by a distance $d$ is given by Coulomb's law as follows: \[F=k\,\frac{|q|\,|q'|}{d^2}\] where $k \approx 8.99\times 10^{9}\,{\rm \frac{N.m^{2}}{C^2}}$ is the Coulomb constant and the magnitudes of charges denoted by $|\cdots|$.
Let the magnitude of charges be $|q_1|=|q_2|=|q|$, Now by substituting the known numerical values of $F$ and distance $d$, and solving for $|q|$ we get
\begin{align*} F&=k\,\frac{|q_1|\,|q_2|}{d^{2}}\\ 9\times 10^{-3}&=(8.99\times 10^{9})\frac{|q|^{2}}{(0.05)^{2}}\\ \Rightarrow q^{2}&=25\times 10^{-16}\\ \Rightarrow q&=5\times 10^{-8}\,{\rm C} \end{align*} In the second equality, we converted the distance from $cm$ to $m$ to coincide with SI units.
The direction of the Coulomb force depends on the sign of the charges. Two like charges repel and two unlike ones attract each other.
Since $q_1$ and $q_2$ have the same signs the electric force between them is repulsive.
Problem (2): What is the electrostatic force between two pieces of grain in a grain elevator if one piece holds a charge of $5\times 10^{-16}\,\rm C$ and the other holds a charge of $2\times 10^{-16}\,\rm C$, while being separated by a distance of 0.06 m?
(a) Find the magnitude of the Coulomb force that one grain exerts on the other.
(b) Is the force attractive or repulsive?
Solution: Known values:\begin{gather*}|q|=2\times 10^{-16}\,{\rm C}\\ |q'|=5\times 10^{-16}\,{\rm C}\\ d=0.06\,{\rm m} \end{gather*}
(a) Coulomb's law gives the magnitude of the electric force between two stationary (motionless) point charges so by applying it we have \begin{align*}F&=k\,\frac{|q|\,|q'|}{d^{2}}\\&=(9\times 10^{9})\,\frac{(2\times 10^{-16})(5\times 10^{-16})}{(0.06)^2}\\&=2.5\times 10^{-19}\,{\rm N}\end{align*}
(b) Since the charges have like signs the electric force between them is repulsive.
If you are getting ready for AP physics exams, these electric force problems are also relevant.
Problem (3): What is the magnitude of the force that a ${\rm 25\, \mu C}$-charge exerts on a ${-\rm 10\,\mu C}$ charge ${\rm 8.5\, cm}$ away? (Take $k=9\times 10^{9}\,{\rm \frac{N.m^{2}}{C^2}}$)
Solution: The magnitude of the attraction/repulsion force between two point charges is given by Coulomb's Law as follows: \begin{align*}F&=k\frac{|qq'|}{r^2}\\&=(9\times 10^{9}){\rm \frac{(25\times 10^{-6}\,C)(10\times 10^{-6}\,C)}{(8.5\times 10^{-2}\,m)^2}}\\&=311.5\quad {\rm N}\end{align*} These two point charges have opposite signs, so the electrostatic force between them is attractive.
Problem (4): Two charged particles apply an electric force of $5.2\times 10^{-3}\,{\rm N}$ on each other. Distance between them gets twice as much as before. What will be Coulomb's force?
Solution: Using Coulomb's law, we have $F=k\frac{|qq'|}{r^2}$, where $r$ is the distance between two charges. We are told in the problem that the distance is doubled so $r_2=2r_1$, thus the electric force is found as \begin{align*}F_2&=k\frac{|qq'|}{r_2^2}\\\\&=k\frac{|qq'|}{(2r_1)^2}\\\\&=\frac 14 \underbrace{k\frac{|qq'|}{r_1^2}}_{F_1}\\\\&=\frac 14 F_1\end{align*}
Problem (5): Two charged point particles are $4.41\,{\rm cm}$ apart. They are moved and placed in a new position. The force between them is found to have tripled. How far apart are they now?
Solution: initial distance is $r_1=4.41\,{\rm cm}$. At the new location, the force is tripled $F_2=3F_1$. Applying Coulomb's law, we have \begin{align*}F_2&=3F_1\\ \\ k\frac{\cancel{|qq'|}}{r_2^2}&=3k\frac{\cancel{|qq'|}}{r_1^2}\\ \\ \frac{1}{r_2^2}&=\frac{3}{(4.41\times 10^{-2})^2}\\\\ \Rightarrow r_2^2&=\frac{(4.41\times 10^{-2})^2}{3}\end{align*} Taking the square root of both sides, we get \[r_2=0.0254\,{\rm m}\] Thus, if those two charges are $2.54\,{\rm cm}$ away, the electrostatic force between them gets tripled.
Problem (6): Two small spheres are charged with the same quantity of charge but of opposite types. The charge on each sphere is $8\times 10^{-7}\,\rm C$ and they are separated by a distance of $\rm 0.75\, m$. Determine the electrical force of attraction between the two spheres.
Solution: Use Coulomb's law and plug in known values and solve for the unknown. \begin{align*} F&=\frac{kq_1 \, q_q}{r^2} \\\\ &=\frac{(9\times 10^9)(8\times 10^{-7})(8\times 10^{-7})}{(0.75)^2} \\\\ &=0.01\,\rm N \end{align*}
Conceptual Problem: A student rubs a balloon against their hair and then touches it to a wall. The balloon adheres to the wall. What is the scientific principle that explains why the balloon sticks to the wall?
Solution: The balloon sticks to the wall due to the principle of static electricity, which can be explained by Coulomb’s law.
When the balloon is rubbed against the student’s hair, it becomes negatively charged due to the transfer of electrons from the hair to the balloon.
When the balloon is then brought near the wall, these extra electrons repel the electrons in the wall, causing the surface of the wall to become positively charged.
Coulomb’s law states that the force between two charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between them.
In this case, the balloon and the wall act like two charges. The negatively charged balloon and the positively charged wall attract each other, and this electrostatic force, as described by Coulomb’s law, causes the balloon to stick to the wall.
Solve these practice problems on the electric charge to get a better view of charges in physics.
Conceptual Problem: Two identical metal spheres, C and D, have charges of $+3.0\times 10^{-6}$ coulomb and $+1.5 \times 10^{-6}$ coulomb, respectively. The magnitude of the electrostatic force on C due to D is $3.6$ newtons. What is the magnitude of the electrostatic force on D due to C?
Solution: According to Newton’s third law of motion, every action has an equal and opposite reaction. This law applies to the forces between charged particles as well. Therefore, the magnitude of the electrostatic force on sphere B due to sphere A is equal to the magnitude of the electrostatic force on sphere A due to sphere B.
This is because the forces are action-reaction pairs according to Newton’s third law, and their magnitudes are determined by the charges on the spheres and the distance between them according to Coulomb’s law.
Therefore, the magnitude of the electrostatic force on sphere B due to sphere A is also 2.4 Newtons, the same as the force on sphere A due to sphere B.
Problem (7): Suppose that two point charges, each with a charge of +1 Coulomb are separated by a distance of
1 meter.
(a) Will they attract or repel?
(b) Determine the magnitude of the electrical force between them.
Solution:
(a) Since the charges are like the electric force between them is repulsive.
(b) The magnitude of electric force between two charges is found by Coulomb's law as follows: \begin{align*} F&=k\frac{|q_1 q_2|}{r^2}\\&=\big(9\times 10^9\big)\frac{1\times 1}{1^2}\\&=9\times 10^9\quad {\rm N}\end{align*}Where $|\cdots|$ denotes the absolute values of charges regardless of their signs.
Problem (8): Two balloons are charged with an identical quantity and type of charge: -0.0025 C. They are held apart at a separation distance of 8 m. Determine the magnitude of the electrical force of repulsion between them.
Solution: applying Coulomb's law and putting the given numerical values in it, we have \begin{align*} F&=k\frac{q_1 q_2}{r^2}\\&=\big(9\times 10^9\big)\frac{(0.0025)(0.0025)}{(8)^2}\\&=879\quad {\rm N}\end{align*}
Problem (9): Two charged boxes are 4 meters apart from each other. The blue box has a charge of +0.000337 C and is attracting the red box with a force of 626 Newtons. Determine the charge of the red box. Remember to indicate if it is positive or negative.
Solution: known information are $q_1=+0.000337\,{\rm C}$, $F=626\,{\rm N}$, and $d=4\,{\rm m}$. Unknown is $q_2=?$. Coulomb's law gets the magnitude of the force between two charges. By applying it and solving for $q_2$, we have \begin{align*} F&=k\frac{q_1 q_2}{d^2}\\ \\ \Rightarrow q_2&=\frac{F\,d^2}{k\,q_1}\\ \\ &=\frac{626\times (4)^2}{(9\times 10^9)(0.000337)}\\ \\&=0.0033\quad {\rm C}\end{align*} Since in the problem said that the force is attraction, so the charge of the red box must be negative.
Note that, Coulomb's law gives only the magnitude of the electric force without their signs.
Problem (10): A piece of Styrofoam has a charge of -0.004 C and is placed 3.0 m from a piece of salt with a charge of -0.003 C. How much electrostatic force is produced?
Solution: the magnitude of the electrostatic force is determined as follows, \begin{align*} F&=k\frac{q_1 q_2}{d^2}\\&=\big(9\times 10^9\big)\frac{(0.004)(0.003)}{(3)^2}\\&=12000\quad {\rm N}\end{align*} Note that in Coulomb's force equation, the magnitude of the charges (regardless of their signs) must be included.
Problem (11): Two coins lie 1.5 meters apart on a table. They carry identical electric charges. Approximately how large is the charge on each coin if each coin experiences a force of 2.0 N?
Solution: Substituting the given numerical into Coulomb's law equation, we have \begin{align*} F&=k\frac{q_1 q_2}{d^2}\\ \\ 2&=\big(9\times 10^9 \big)\frac{q\,q}{(1.5)^2}\\ \\ \Rightarrow q&=\sqrt{\frac{2\times (1.5)^2}{9\times 10^9}}\\ \\ &=2.23\times 10^{-5} \quad {\rm C} \end{align*}
The following problems are for practicing for the AP Physics C problems.
Problem (6): Three point charges are placed at the corners of an equilateral triangle as in the figure below. What is the magnitude and direction of the net electric force on the $2\,\rm \mu C$ charge?
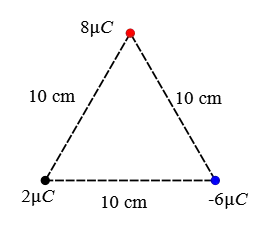
Solution: The force that the charge $-6\,\rm \mu C$ applies to the $2\,\rm \mu C$ is attractive and to the right along the line connecting them and its magnitude is also calculated as follows: \begin{align*} F_{2,-6}&=k\frac{qq'}{r^2} \\\\ &=(9\times 10^9) \frac{(2\times 10^{-6})(6\times 10^{-6})}{(0.10)^2} \\\\ &=10.8\,\rm N \end{align*} The charge $8\,\rm \mu C$ is repelled the charge $2\,\rm \mu C$ along the line joining them with a magnitude of \begin{align*} F_{2,8}&=k\frac{qq'}{r^2} \\\\ &=(9\times 10^9) \frac{(2\times 10^{-6})(8\times 10^{-6})}{(0.10)^2} \\\\ &=14.4\,\rm N \end{align*} Given the geometry shown below, the force $\vec{F}_{2,8}$, denoted by $\vec{F}_8$ for simplicity, makes an angle of $60^\circ$ with the negative direction of $x$-axis.
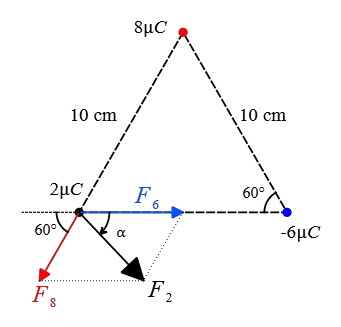
Resolving this vector force along the horizontal and vertical directions gives its components \begin{align*} F_{1x}&=F_1 \cos 60^\circ \\ &=14.4\times (0.5)=72.2\,\rm N \\\\ F_{1y}&=F_1 \sin 60^\circ \\&=14.4\times (\frac{\sqrt{3}}{2})=72.2\sqrt{3}\,\rm N \end{align*} The net electric force on the charge $2\,\rm \mu C$ is the vector sum of individual forces due to other charges (superposition principle) \[\vec{F}_2=\vec{F}_8+\vec{F}_6 \] Adding the vectors along the horizontal and vertical directions give the corresponding components of the net electric force. \begin{align*} F_{2x}&=10.8+(-72.2) \\&=28.6\,\rm N \\\\ F_{2y}&=0+(-72.2\sqrt{3}) \\&=-72.2\sqrt{3} \,\rm N \end{align*} Given these components, we can find the magnitude and direction of the net electric force the desired charge \begin{align*} F_2&=\sqrt{F_{2x}^2+F_{2y}^2} \\\\ &=\sqrt{(28.6)^2+(-72.2\sqrt{3})^2} \\\\&=32.16\,\rm N \end{align*} and its direction with the positive $x$-direction as follows: \begin{align*} \alpha &=\tan^{-1}\left(\frac{F_{2y}}{F_{2x}}\right) \\\\ &=\tan^{-1}\left(\frac{72.2\sqrt{3}}{28.6}\right) \\\\ &=77^\circ \end{align*}
Problem (7): A $2-\rm \mu C$ point charge and another point charge of magnitude $4-\rm \mu C$ are a distance $L=1\,\rm m$ apart. Where should a third point charge be placed so that the net electric force on it is zero?
Solution: This is a tricky question and is more similar to the AP Physics C questions. We solve this problem by assuming the third point charge is positive.
Simple reasoning shows that between the charges the net force on the third charge points to the right and adds together rather than canceling each other. Thus, this region is removed.
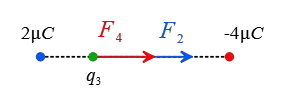
Now, assume a point somewhere outside the charges and closer to the smaller one at a distance $x$ from it. The following figure shows that the forces on this hypothetical positive charge are clearly in opposite directions.
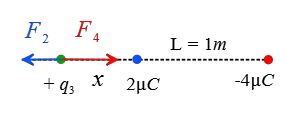
\begin{gather*} F_2=F_4 \\\\ k\frac{q_3 q_2}{x^2}=k\frac{q_3 q_4}{(L+x)^2} \\\\ \frac{2}{x^2}=\frac{4}{(1+x)^2} \\\\ (1+x)^2=2x^2 \\\\ \Rightarrow \boxed{x^2-2x-1=0} \end{gather*} The above quadratic equation has two solutions \[x_1=2.41\,\rm m \quad , \quad x_2=-0.4\,\rm m\] The negative in the second solution means that we must go back to the region between the charges that is not acceptable. Thus, outside the charges and somewhere close to the smaller charge we can find a point where the net Coulomb force on the third charge is zero.
For practice, consider yourself a negative charge, repeat the above steps, and find the result.
Problem (8): In the following figure, a small sphere of mass $3\,\rm g$ and charge of $q_1=15\,\rm nC$ are suspended by a light string over the second charge of equal mass and charge of $-85\,\rm nC$. The distance between the two charges is $2\,\rm cm$.
(a) Find the tension in the string.
(b) What is the smallest value of separation $d$, assuming the string can withstand a maximum tension of $0.150\,\rm N$?
Solution: The negative charge and gravity pull vertically down the positive charge and the tension in the string pulls up, as depicted in the following free-body diagram.
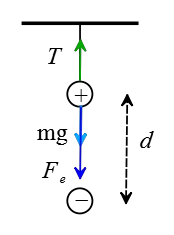
(a) The positive charge is motionless so the net force on it must be zero. Balancing the above forces applied to it gives the tension force in the string. \begin{gather*} T=F_e+mg \\\\ T=k\frac{q_1 q_2}{r^2}+mg \\\\ T=(9\times 10^9) \times \frac{(15\times 10^{-9})(85\times 10^{-9})}{(0.02)^2}+(0.003)(10) \\\\ \Rightarrow \boxed{T=0.31\,\rm N} \end{gather*}
(b) This time, the maximum tension force that the string can withstand is given and asked to find the smallest distance between the charges.
Again we use the above relation between the forces on the positive force and solve for the unknown distance $d$. \begin{gather*} T=k\frac{q_1 q_2}{r^2}+mg \\\\ T-mg=k\frac{q_1 q_2}{r^2} \\\\ r^2=k\frac{q_1 q_2}{T-mg} \end{gather*} Taking the square root of both sides and substituting the numerical values gives \begin{align*} r&=\sqrt{\frac{(9\times 10^9)(15\times 10^{-9})(85\times 10^{-9})}{0.150-(0.003)(10)}} \\\\ &=0.97\,\rm m \end{align*}
In summary, Coulomb's law is fundamental for solving an electrostatic problem in the case of some arrangements of point charges. The following PDF is tailored for the college level and is difficult.
Author: Dr. Ali Nemati
Last Updated: Feb 3, 2024
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
