- Home
- Physics Problems
- Problems
Solved Problems
A large piece of cork weighs $0.285\,{\rm N}$ in air. When held submerged underwater by a spring scale, the scale reads $0.855\,{\rm N}$. Find the density of the cork.
Draw a free body diagram as shown in the figure:
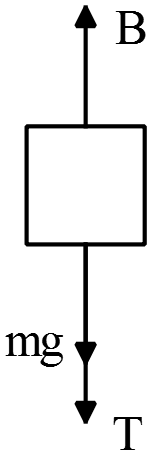
Apply Newton's second law to the cork:\[\Sigma F_y=0\Rightarrow B=mg+T\] Where $T$ is tension in the spring scale and $B$ is buoyancy force.
Buoyancy force: when a rigid object is submerged in a fluid (completely or partially), there exists an upward force on the object that is equal to the weight of the fluid that is displaced by the object, i.e., $B=\rho_{fluid}V_{submerged}\,g$
The mass of the cork is known (weight measured in the air), so using the buoyancy force formula we can find its volume.
\begin{gather*} B=mg+T=\rho_{water}V_{cork}g \\ \\ 0.285+0.855=1000\times 9.8\times V_{cork} \\ \\ V_{cork}=1.16\times {10}^{-4}\quad {\rm m^3}\end{gather*}
Given the $V_{cork}$, one can determine the density of the cork by \begin{gather*} \rho_{cork}=\frac{m_{cork}}{V_{cork}}=\frac{W_{cork}}{gV_{cork}}\\ \\ \rho_{cork}=\frac{0.285}{9.8\times 1.16\times {10}^{-4}}=250.7\,{\rm kg/m^3}\end{gather*}
An object of volume $0.2\, \rm m^3$ is completely submerged in a fluid with density $500\,\rm kg/m^3$. Compute the buoyant force of the fluid on the object.
Recall from Archimedes's principle examples, that the buoyant force is equal to the weight of the displaced fluid.
In this case, since the object is totally submerged so the volume of the displaced fluid and object is the same.
Remind that the weight of an object is mass times g and mass is density times volume of an object.
Applying buoyant force formula gives \begin{align*}F_B&=\underbrace{\rho_{fluid}V_{submerged}}_{M}g\\ \\ &=500\times 0.2\times 9.8=980\quad {\rm N}\end{align*}
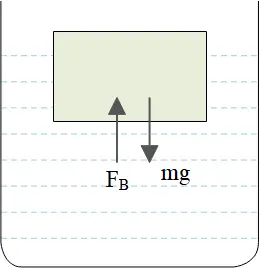
A 1.5 kg block of wood floats on water with 68 percent of its volume submerged. A lead block is placed on the wood, fully submerging the wood to a depth where the lead remains entirely out of the water. Find the mass of the lead block.
By applying Archimedes' principle and Newton's second law, we can solve this problem.
Stage (1): before loading the lead block, Newton's second law states that in the vertical direction there is no motion.
On the other hand, recall from Archimedes' principle problems that the buoyant force equals to the weight of displaced fluid.
\begin{gather*} \Sigma F_y=0 \\ \\ F_B-m_{block}g=0\\\\ \Rightarrow \rho_{water}V_{sub}g=m_{block}g \\\\ \Rightarrow \quad \rho_{water}\left(0.68\ V_{block}\right)=m_{block} \\\\ \rho_{water}V_{block}=\frac{m_{block}}{0.68}\end{gather*}
Stage (2): after loading \begin{gather*} \Sigma F_y=0\\\\ \left(m_{lead}+m_{block}\right)g=F_B=\rho_{water}V_{block}g\\\\ \Rightarrow m_{lead}=\rho_{water}V_{block}-m_{block}\end{gather*}
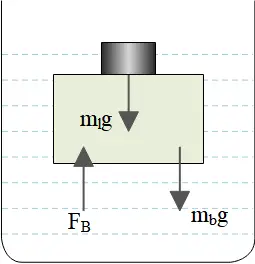
Now substituting stage 1 into the stage 2, we obtain
\begin{align*} m_{lead}&=\frac{m_{block}}{0.68}-m_{block}\\\\&=1.5\times 0.47\\\\&=0.71\quad {\rm kg}\end{align*}
A spherical shell of copper with an outer diameter of $12\, {\rm cm}$ floats on water with half its volume above the water's surface. Determine the inner diameter of the shell. The cavity inside the spherical shell is empty.[$\rho_{water}=1000\,\frac{{\rm kg}}{{{\rm m}}^{{\rm 3}}}\ ,\ \ \rho_{copper}=8940\,\frac{{\rm kg}}{{{\rm m}}^{{\rm 3}}}$]
The volume of displaced water is equal to the volume of the object that is submerged i.e. $\frac{1}{2}\left(\frac{4}{3}\pi R^3_1\right)$.
Because the object is motionless (in equilibrium) so $\Sigma F_y=0$
\[mg=F_B=\rho_wV_{subm}g\]
\[\rho_{copper}V_{shell}g=\rho_wV_{subm}g\]
\[\rho_{copper}\frac{4}{3}\pi\left(R^3_1-R^3_2\right)=\rho_w\frac{1}{2}\left(\frac{4}{3}\pi R^3_1\right)\Rightarrow \ R^3_2=R^3_1\left(1-\frac{1}{2}\frac{\rho_w}{\rho_{copper}}\right)\]
\[\therefore R_2={\left({\left(0.12\right)}^3\left(1-\frac{1}{2}\frac{1000}{8940}\right)\right)}^{\frac{1}{3}}=0.118\ {\rm m}= 11.8\ {\rm cm}\]
Where $\frac{4}{3}\pi(R^3_1-R^3_2)$ is the volume of the spherical shell with outer radius $R_1$ and inner radius $R_2$.
A solid cylinder (radius $=0.150\,{\rm m}$, height=$0.120\,{\rm m}$) has a mass of $6.5\,{\rm kg}$. This cylinder is floating in the water. Then oil ($\rho=725\, {\rm kg/}{{\rm m}}^{{\rm 3}}$) is poured on top of the water until the situation shown in the drawing results. How much of the height of the cylinder is in the oil?
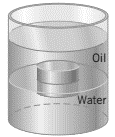
Here there is two buoyant force acting on the cylinder that must be balanced by the weight of the cylinder (since the cylinder is in equilibrium) i.e. $\Sigma F_y=0$
\begin{gather*}F_{Bo}+F_{Bw}=W_{cyl} \\ \\ \rho_oV_{sub,o}g+\rho_wV_{sub,w}g=m_{cyl}g \end{gather*} Where the above volumes are submerged volumes of the cylinder in the oil and water.
Because the cylinder totally submerged in the fluids ,$V_{sub,o}+V_{sub,w}=V_{cyl}$
Therefore from the above equations, we obtain
\[\rho_o\left(V_{cyl}-V_{sub,w}\right)+\rho_wV_{sub,w}=m_{cyl}\]
\begin{align*} \Rightarrow V_{sub,w}&=\frac{m_{cyl}-\rho_oV_{cyl}}{\rho_w-\rho_o}\\ &=\frac{6.5-725\times \left(\pi{\left(0.15\right)}^2\times 0.12\right)}{1000-725}\\ &=1.27\times {10}^{-3}\,\rm m^3 \end{align*} Use the definition of the volume of the cylinder to find its height \begin{align*} h_w&=\frac{V_{sub,w}}{\pi r^2}\\ \\ &=\frac{1.27\times {10}^{-3}}{p\times {\left(0.15\right)}^2}\\ \\ &=0.018\quad{\rm m}\end{align*} The sum of the submerged heights in the oil and water is the height of the cylinder. \[h_w+h_o=H_{cyl}\Rightarrow h_o=0.12-0.018=0.102\ {\rm m}\]
$h_o$ is the height of the cylinder floating in the oil.
Suppose that the radius of the pulmonary artery decreases to $80\%$ the original radius owing to cholesterol buildup. By how much would the pressure change to maintain the original flow rate of blood through the artery? (a pressure difference of $450\, {\rm Pa}$ exist across the length of the pulmonary artery)
Because the flux passing through the artery is constant, so if we called $I_V$ as the volume flow rate then the Poiseuille's law states
\[\Delta P=\frac{\eta L}{\pi r^4}I_V\]
\[{\left(I_V\right)}_{obst}={\left(I_V\right)}_{free}\to \frac{\pi R^4_{obst}\Delta P_{obst}}{8\eta L}=\frac{\pi R^4_{free}\Delta P_{free}}{8\eta L}\]
\[R^4_{obst}\Delta P_{obst}=R^4_{free}\Delta P_{free}\]
\[\Delta P_{obst}=\Delta P_{free}{\left(\frac{R_{free}}{R_{obst}}\right)}^4=450{\left(\frac{1}{0.8}\right)}^4=1048\ {\rm Pa}\]
\[\therefore \Delta P_{obst}-\Delta P_{free}=\left(1048-450\right)=648\ {\rm Pa}\]
The aorta has an inner radius of approximately $0.25\, {\rm cm}$. the average speed of blood through the aorta is $1.0\, {\rm m/s}$. A capillary has an inner radius of approximately $5$ microns ($5\times {10}^{-6}\, {\rm m}$) and the average speed of blood through a capillary is $1.0\, {\rm cm/s}$. Assuming that all the blood flowing through the aorta flows through the capillaries, determine the number of capillaries in the circulatory system.
Because all the blood flowing through the aorta flows through the capillaries, then the volume flux is conserved. By definition, volume flux ($I_V$) is equal to the area of the tube times the speed of fluid through it.
Thus,in this case we have
\[{\left(I_V\right)}_{aorta}={\left(I_V\right)}_{capillaries}\]
\[{\left(A\times v\right)}_{aorta}=N{\left(A\times v\right)}_{capillary}\]
\[N_{capillary}=\frac{A_{aorta}\times v_{aorta}}{A_{capillary}\times v_{capillary}}=\frac{\left(\pi r^2_{aorta}\times v_{aorta}\right)}{\pi r^2_{capillary}\times v_{capillary}}\]
\[=\frac{{\left(0.25\times {10}^{-6}\right)}^2\times 1}{{\left(5\times {10}^{-6}\right)}^2\times {10}^{-2}}=2.5\times {10}^7\ \]
The pulmonary artery, which connects the heart to the lungs, is $8.5\, {\rm cm}$ long and has an inner radius of $2.4\, {\rm mm}$. If a pressure difference of $450\, {\rm Pa}$ exist across the length of the pulmonary artery, what is the average speed of the blood flowing through it? ($\eta_{Blood}=0.004\ {\rm Pa.s}$)
Use the Poiseuille's law to determine how the pressure drop relates to the flux $I_V$
\[I_V=Av=\frac{\pi R^4\Delta P}{8\eta L}\]
\[v=\frac{\pi R^4\Delta P}{8\eta L}\frac{1}{A}=\frac{\eta R^4\Delta P}{8\eta L}\frac{1}{\eta R^2}=\frac{R^2\Delta P}{8\eta L}\]
\[=\frac{{\left(2.4\times {10}^{-3}\right)}^2\times 450}{8\times 4\times {10}^{-3}\times 8.5\times {10}^{-2}}=0.45\frac{{\rm m}}{{\rm s}}\]
The water flows straight downward out the end of circular pipe of radius $r=2\,{\rm mm}$ and velocity $v_0=1\, {\rm m/s}$. It flows in a continuous column, without breaking into drops.
(a) What is the flow rate in this column?
(b) What is the radius of the column a distance $H=\frac{1}{2}\,{\rm m}$ below the pipe?
(a) In an incompressible fluid, the volume flow rate is defined as $I_V=Av$, where $v$ is the velocity of the fluid perpendicular to the cross-sectional area $A$. Therefore,
\begin{align*} I_V&=A_{disk}v\\ \\ &=\left(\pi r^2\right)v\\ \\ &=\pi{\left(0.002\right)}^2\left(1\right)\\ \\&=1.256\times {10}^{-3}\quad {\rm m^3/s}\end{align*}
(b) Use the Bernoulli equation, $P+\rho gh+\frac{1}{2}\rho v^2={\rm Constant}$ at the two points to find the velocity of the water at $H$, then given that the volume flow rate is constant determines the desired radius! At $h=H/2$, we have \[P_h+\rho gh+\frac{1}{2}\rho v^2=Constant\] and at $h=0$, \[P_0+\frac{1}{2}\rho v^2_0=Constant\]
\begin{gather*} \Rightarrow \ quad P_h+\rho gh+\frac{1}{2}\rho v^2=P_0+\frac{1}{2}\rho v^2_0 \\ \\ \Rightarrow\quad v={\left(v^2_0+2gh\right)}^{\frac{1}{2}}={\left(1^2+9.8\times 0.5\right)}^{\frac{1}{2}}=\ 3.286\ \frac{{\rm m}}{{\rm s}}\end{gather*} Since the initial and final entry are open to air so the air pressure at these points is the same that is $P_h=P_0$. \begin{align*} {\left(I_V\right)}_{ini}&={\left(I_V\right)}_{fin} \\ \\ \Rightarrow \quad A_iv_i&=A_fv_f \\ \\ \Rightarrow \quad \left(\pi r^2_i\right)v_i&=\left(\pi r^2_f\right)v_f \end{align*} Thus, the radius of the column at that distance is \begin{align*} r_f&={\left(\frac{v_i}{v_f}\right)}^{\frac{1}{2}}r_i\\ &=(0.002)\sqrt{\frac{1}{3.286}}\\ \\&=1.1{\rm mm}\end{align*}
Two identical vertical tubes are connected by a small horizontal tube as shown in the figure. The tubes are open at the top. Equal volumes of liquids with densities $\rho_1=4800\, {\rm kg/m^3}$ and $\rho_2=800\,{\rm kg/m^3}$ are at sitting at rest in the tubes. The height $H=2\, {\rm m}$ and ${\rm 1\,atm=1.013\times 10^{5}\,Pa}$.

(a) What is the pressure at the bottom of fluid $2$?
(b) What is the height $h_A$?
(c) A ball of radius $R=1\, {\rm cm}$ and density $\rho_b=1200\, {\rm kg/m^3}$ is dropped into the left tube. The viscosity of the top fluid is $\eta_2=0.03\ {\rm Pa.s}$. While the ball is in fluid $2$, what is its terminal velocity?
(a) The pressure at a point $h$ below the free surface of a fluid is given by $P=P_0+\rho gh$, where $P_0$ is the air pressure. Therefore \begin{align*} P&=1.013\times {10}^5+800\left(9.8\right)\left(2\right)\\ \\ &=1.17\times {10}^5\ {\rm Pa}\end{align*}
(b) Since the fluids are at equilibrium (motionless) so the pressure at the bottom of the tubes must be the same so \begin{gather*} P_1=P_2 \\ \\ \Rightarrow P_0+\rho_1gh_A=P_0+\rho_2gH+\rho_1gh \\ \\ \rho_1h_A=\rho_2H+\rho_1h \\ \\ \Rightarrow h_A=\frac{\rho_2}{\rho_1}H+h\end{gather*} Since stated that there is equal volume thus \begin{gather*} V_1=V_2 \\ \\ \Rightarrow HA=\left(h_A+h\right)A \\ \\ \Rightarrow H=h_A+h \\ \\ \Rightarrow\quad h_A=\frac{\rho_2}{\rho_1}H+h \\ \\ \xrightarrow{H=h_A+h} h_A=\frac{\rho_2}{\rho_1}H+\left(H-h_A\right) \\ \\ \Rightarrow h_A=\frac{1}{2}H\left(\frac{\rho_2}{\rho_1}+1\right) \end{gather*} Therefore, we get \[h_A=\frac{1}{2}\left(2\right)\left(\frac{800}{4800}+1\right)=1.167\ {\rm m}\]
(c) The three forces acting on the ball are, buoyancy force $F_b$, Drag force $F_D$, and gravity. Terminal velocity means that the acceleration of the ball must be zero so the net force on the ball is zero i.e. $\Sigma F_{net}=0$
\begin{gather*} \Sigma F_y=0 \\ \\ F_D+F_b-mg=0 \\ \\ 6\pi\eta Rv+\rho_2V_{sub}g-mg=0 \\ \\ \Rightarrow v_T=\frac{m-\rho_2V_{sub}}{6\pi\eta R}g\end{gather*} Using the definitions of mass and density $m=\rho V$, we have \begin{align*} v_T&=\frac{\left(\rho_b-\rho_2\right)\left(\frac{4}{3}\pi R^3\right)}{6\pi\eta R}g\\ \\&=\frac{2}{9}\left(\rho_b-\rho_2\right)\frac{R^2g}{\eta}\\ \\ &=\frac{2}{9}\left(1200-800\right)\frac{{\left(0.01\right)}^2\left(9.8\right)}{0.03}\\ \\&=2.90\quad {\rm m/s}\end{align*}
A spherical ball has a mass of $2.66\, {\rm kg}$ and a radius of $3.34\, {\rm cm}$. This ball is suspended from a weight scale.
(a) What would be the weight of this ball as measured in the air?
(b) What is the volume of this ball in $\rm m^3$?
(c) The ball, still suspended from the scale, is now immersed in fresh water. Calculate the effective weight of the ball for this situation. ($\rho_w=1000\,\rm kg/m^3$)
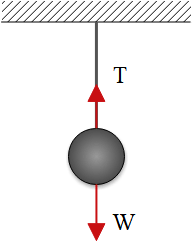
(a) The weight of an object that is suspended from a string (scale) equals the tension in the string i.e. $\Sigma F_y=0\Rightarrow T-W=0$
\[\Rightarrow \ \ T=mg=2.26\times 9.8=26.1\ {\rm N}\]
(b) The volume of the sphere is defined as \begin{align*} V&=\frac{4}{3}\pi r^3\\ \\ &=\frac{4}{3}\pi{\left(3.34\times {10}^{-2}{\rm m}\right)}^2\\ \\&=1.56\times {10}^{-4}\quad {\rm m^3}\end{align*}
(c) There is a buoyancy force acting on the objects in the fluids. This force equals the weight of the displaced fluid.
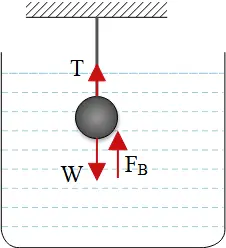
Therefore, \begin{align*} \Sigma F_y=0 &\Rightarrow \ T+F_b-mg=0\\ &\Rightarrow T=mg-\rho V_{sub}g\\ &=26.1-\left({10}^3\times 1.56\times {10}^{-4}\right)\left(9.8\right)\\ &=24.57\ {\rm N} \end{align*} Where $V_{sub}$ is the amount of volume that submerged in the water.
A water tank is filled to a height of h=2.2 m. The air in the tank above the 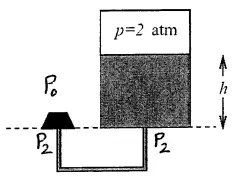 water is kept at a constant pressure of $P=2.0\, {\rm atm}$. The diameter of the U shaped is $3.0\, {\rm cm}$. Initially a weight is put on the open end of the pipe, which temporarily prevents the water from flowing out. ($\rho_w=1000\, {\rm kg/}{{\rm m}}^{{\rm 3}}$, $1\, {\rm atm=}{{\rm 10}}^{{\rm 5}}\ {\rm Pa}$ , $P_0=1\,{\rm atm}$)
water is kept at a constant pressure of $P=2.0\, {\rm atm}$. The diameter of the U shaped is $3.0\, {\rm cm}$. Initially a weight is put on the open end of the pipe, which temporarily prevents the water from flowing out. ($\rho_w=1000\, {\rm kg/}{{\rm m}}^{{\rm 3}}$, $1\, {\rm atm=}{{\rm 10}}^{{\rm 5}}\ {\rm Pa}$ , $P_0=1\,{\rm atm}$)
(a) What is the pressure at the bottom of the tank?
(b) Calculate the minimum value of the weight $W$, so that it isn't pushed away by the pressure of the water.
(c) The weight is removed, and the water starts to flow out of the open end of the pipe. Determine the velocity $v$ of the water just after it leaves the pipe.
(d) What is the flow rate?
(a) The pressure at depth $h$ below the surface of a fluid is given by $P=P_0+\rho gh$ where $P_0$ is the air pressure. So
\begin{align*} P_2&=P+\rho gh\\ \\&=\left(2\times {10}^5\right)+1000\times 9.8\times 2.2\\ \\&=2.21\times {10}^5\ {\rm Pa}\end{align*}
(b) The force acting on the open end of the tube due to the tank ($P_2A$) and air ($P_0A$) must be balanced with the weight of $W$. So using the definition of pressure we have \begin{align*} F_{net} &=A\Delta P=A\left(P_2-P_0\right)=\pi{\left(\frac{d}{2}\right)}^2\left(P_2-P_0\right)\\ &\Rightarrow F_{net}=\pi{\left(\frac{0.03}{2}\right)}^2\left(2.21-1\right)\times {10}^5=86.2\ {\rm N} \end{align*} Thus,\[W=F_{net}=86.2\, {\rm N}\to {\rm \ \ W=mg}\Rightarrow {\rm m=8.8\ kg}\]
(c) Use the Bernoulli's equation at points A and B
\[P_A+\rho gh_A+\frac{1}{2}\rho v^2_A=P_B+\rho gh_B+\frac{1}{2}\rho v^2_B\]
Let the base to be as shown in the figure, so $h_A=h_B=0=v_B$
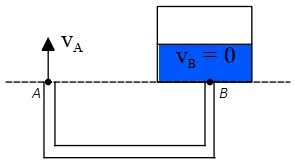
\begin{align*} &\Rightarrow \frac{1}{2}\rho v^2_A=P_B-P_A\\ &\Rightarrow z_A=\sqrt{\frac{2\left(P_B-P_A\right)}{\rho}}=\sqrt{\frac{2\left(2.21-1\right)\times {10}^5}{1000}}\\ &=15.55\quad {\rm m/s} \end{align*}
(d) The flow rate is defined as $Q=Av$ so
\begin{align*} Q &=\pi r^2v=\pi{\left(\frac{d}{2}\right)}^2v\\ &=\pi{\left(\frac{0.03}{2}\right)}^2\times 15.6\\ &=0.099\quad {\rm m^3/s} \end{align*}
A cubic block of ice (each side, s=1 m) floats in a lake. The density of ice is $917\, {\rm kg/m^3}$ and the density of lake water is $1000\,{\rm kg/m^3}$.
(a) How far ($s-x_0$) does the top of the ice block lie above the water level?
(b) Now assume that the block has been pushed further $x$ distance into the water. When released, the block will bob up and down. What is the net force on the ice block when it is $x$ distance below its equilibrium position?
(c) Using the analogy to a spring force, what is the angular frequency of bobbing?
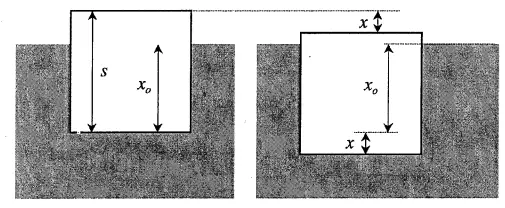
(a) Two forces acting on the ice block, buoyancy $F_B$, and gravity (which is the weight force). These forces must be in balance (the ice block does not accelerate). Recall from buoyant force formula, that $F_B=\rho_f V_{dis}g$. Thus, balancing these two forces $F_B=W$, get
\begin{align*} \rho_wV_{sub}g=\underbrace{\rho_{ice}V_{ice}g}_{W}\Rightarrow \rho_wx_0A=\rho_{ice}As\\ \Rightarrow x_0=\frac{\rho_{ice}}{\rho_w}s=\frac{917}{1000}\left(1\right)=0.917\ {\rm m}\\ \therefore s-x_0=1-0.917=8.3\ {\rm cm} \end{align*}
In the above, $V_{sub}$ is the submerged volume of the ice in the water and $A=s^2$ is the cross-sectional area of the ice block.
(b) In this case, since the ice block is moved away from the equilibrium so there is a net force on the block as
\begin{align*}F_{net}&=F_B-W\\ \\ &=\rho_wA\left(x_0+x\right)g-\rho_{ice}Asg\end{align*} From part (a) we know that $\rho_wx_0A=\rho_{ice}As$ so
\[F_{net}=-\rho_ws^2gx\] We have inserted a minus to show that the force and displacement are in opposite directions. In the other words $F_{net}$ is a restoring force like the spring force in Hook's law.
(c) As mentioned in part (b), the $F_{net}$ is similar to the spring force $F_S=-kx$ so
\begin{align*}F_{net}&=F_S\\ \\ -\rho_ws^2gx&=-kx\\ \\ \Rightarrow \quad k&=\rho_ws^2g\end{align*} In the springs the angular frequency is defined as
\begin{align*} \omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{\rho_ws^2g}{\rho_{ice}s^3}}=\sqrt{\frac{\rho_wg}{\rho_{ice}s}}\\ \\ \therefore \quad \omega=\sqrt{\frac{1000\times 9.8}{917\times 1}}=3.26\quad {\rm rad/s} \end{align*} Where $m=\rho_{ice}V=\rho_{ice}s^3$ is the mass of the ice block.
(a) A water tank ($\rho_{water}=\,1000{\rm kg/m^3}$ ) is placed on top of a hill, as shown in the figure.
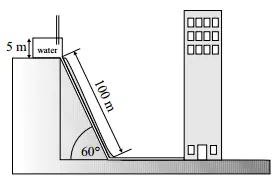
The atmospheric pressure is $P_{atm}=1.013\, \times \ {10}^5\ {\rm N/}{{\rm m}}^{{\rm 2}}$ . The level of the water in the tank is $5.00\ {\rm m}$ high. The length of the pipe is $100\, {\rm m}$, and the inclination is $\theta\ =\ 60.0{}^\circ $ .
(b) Determine the pressure in the pipe at the bottom of the hill. Assume that the water is not flowing through the pipe (static case).
(c) At what velocity will the water exit from a faucet on the sixth floor, $41\, {\rm m}$ above the ground?
(a) The pressure at depth $h$ in a fluid with density $\rho$ is given by $P=P_0+\rho gh$. In this problem, the distance between the bottom of the pipe and the free surface of water is \begin{align*}h_{tot}&=h_{tank}+l_{pipe}\,{\sin 60^\circ}\\ &=5+100\,{\sin 60^\circ}\\ &=91.6\quad {\rm m} \end{align*} Therefore, \begin{align*} P_{Bottom} &=P_0+\rho gh_{tot}\\ &=1.013\times {10}^5+\left({10}^3\right)\left(9.8\right)\left(91.6\right)\\ &=9.99\times {10}^5\quad {\rm N/m^2} \end{align*} (b) Use the Bernoulli's equation between the 6${}^{th}$ floor and end of the pipe.
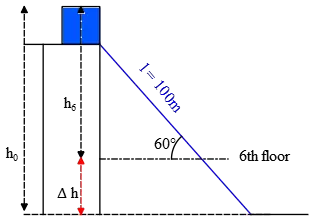
Since the faucet is open to atmosphere so $P_6=P_0=1\,{\rm am}$
\begin{gather*} P_0+\frac{1}{2}\rho v^2_0+\rho gh_0=P_6+\frac{1}{2}\rho v^2_f+\rho gh_6 \\ \\ g(\underbrace{h_0-h_6}_{\Delta h})=\frac{1}{2}v^2_f \\ \\ \Rightarrow v_f=\sqrt{2g(h_0-h_6)}=\sqrt{2\times 9.8\times (91.6-41)}=31.49\quad {\rm m/s}\end{gather*} Where $\Delta h$ is the distance shown in the figure. (Since, as mentioned, the water in the pipe is in steady state, $v_0=0$)
A man is sitting in a boat on a swimming pool. In the boat there is a rock of mass $M =100\, {\rm kg}$ and density ${\rho }_{{\rm rock}}=5.00\times{10}^{3}\,{\rm \ kg/}{{\rm m}}^{{\rm 3}}$. He throws the rock into the water. By what amount and in what direction will the water level of the pool change? The density of water is ${\rho }_{{\rm water}}=10^{3}\,{\rm kg/}{{\rm m}}^{{\rm 3}}$ and the area of the pool surface is ${\rm 50.0\ }{{\rm m}}^{{\rm 2}}$ .
Notes: a floating object displaces its own weight of water and a submerged object displaces its own volume of water. Therefore, in the case that the rock is in the boat the volume of the displaced water is
\[\Delta V_{in}=\frac{m_{rock}}{\rho_w}=\frac{100}{1000}=0.1\ {{\rm m}}^{{\rm 3}}\]
And when the rock is thrown into the water
\[\Delta V_{out}=\frac{m_{rock}}{\rho_{rock}}=\frac{100}{5\times {10}^3}=0.02\ {{\rm m}}^{{\rm 3}}\]
Thus the total change in the water level is $\Delta V_{tot}=\Delta V_{in}-\Delta V_{out}$.
\[\Delta {{\rm V}}_{{\rm tot}}{\rm =0.1-0.02=0.08\ }{{\rm m}}^{{\rm 3}}\]
Using the definition of the volume of a rectangular shape, we obtain the change in the water level of the pool
\[\Delta V_{tot}=A\Delta h\Rightarrow \Delta h=\frac{\Delta V_{tot}}{A}=\frac{0.08}{50}=1.6\times {10}^{-3}\ {\rm m}\]
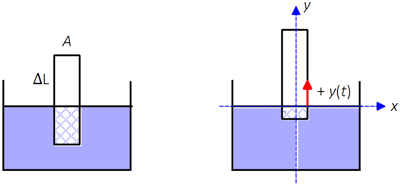
A meter-stick with a density of $700\, {\rm kg/m^3}$ is lowered end on into a swimming pool filled with water.
(a) How much of the meter stick is above the water when the meter stick reaches static equilibrium with the water?
(b) If the meter stick is raised $10\, {\rm cm}$ above its equilibrium position and released, with what period does it oscillate?
(c) For the condition above, what is the maximum speed of the oscillation of the meter stick?
(a) Static equilibrium reaches when the buoyant and gravity force acting on the object are balanced by each other. By definition, the buoyant force is equal to the weight of the fluids displaced by a submerged object in that fluid. Let the amount of the stick meter above the water be $\Delta L$ and the total length of it be $L$. Therefore,
\begin{align*} F_g=F_B\to \underbrace{\rho V}_{M}g=\underbrace{\rho_wV_{sub}}_{M_{sub}}g\\ \rho ALg=\rho_wA\left(L-\Delta L\right)g\Rightarrow \Delta L=\frac{\rho_w-\rho}{\rho_w}L\\ \Delta L=\frac{1000-700}{1000}\left(1\right)=0.3\ {\rm m=30\ cm}\\ \end{align*} Where $A$ is the cross-sectional area of the meter stick and $M_{sub}$ is the amount of the meter stick submerged in the water.
(b) Since the meter stick moved away from the equilibrium position so there is a net force on it.
If the submerged height is greater than the equilibrium height ($L-\Delta L$) then $F_B>mg$ and the object accelerates upward or vice versa.
Let us assume the $y$ axis is in the upward direction. Since at the instant that the meter stick is pulled up by $y(t)$, the buoyant force is smaller than the weight of the meter stick so there is net force toward the $-y$ axis. Using Newton's second law and applying Archimedes principle formula, we obtain \begin{align*} \Sigma F=Ma\to F_B\hat{j}+W\left(-\hat{j}\right)=Ma\left(-\hat{j}\right)\\ \rho_wA\left(L-\Delta L+y(t)\right)g-\rho ALg=-\rho AL\frac{d^2y(t)}{dt^2}\\ \end{align*} From part (a), we can rearrange the relation above as follows \[\Rightarrow \rho AL\frac{d^2y(t)}{dt^2}=-\rho_wAy(t)g\Rightarrow \frac{d^2y(t)}{dt^2}=-\frac{\rho_wg}{\rho L}y(t)\] This is similar to the equation of simple harmonic motion $\frac{d^2x}{dt^2}+\omega^2x=0$ where $\omega$ is the angular velocity and is related to the period of the motion by $\omega=2\pi/T$ so
\[T=2\pi\sqrt{\frac{\rho L}{\rho_wg}}=2\pi\sqrt{\frac{700\times 1}{1000\times 9.8}}=1.68\ {\rm s}\]
(c) In above the equation of motion of the meter stick is as the harmonic motion that is $y\left(t\right)=A\,{\sin \omega t\ }$, where $A$ is the maximum displacement of the body from equilibrium position that in this case is $10\, {\rm cm}$. By taking time derivative of $y(t)$, we can find the equation of the velocity of the object as $v\left(t\right)=A\omega\,{\cos \omega t\ }$ where $A\omega$ is the maximum speed. So in this case \begin{align*} v_{max}&=A\omega=0.1\times \sqrt{\frac{\rho_wg}{\rho L}}\\ &=0.1\times \sqrt{\frac{1000\times 9.8}{700\times 1}}\\ &=0.374\quad {\rm m/s} \end{align*}
Four liters of liquid helium are stored at their boiling point temperature of $4.2\, {\rm K}$ in a spherical container of radius $0.1\, {\rm m}$. The container is perfect black body absorber. The container is surrounded by a spherical shield whose temperature is $77\ {\rm K}$. This shield is a perfect black body. A vacuum exists in space between the container and the shield. $L_V=2.1\times {10}^4\, {\rm J/K}$ and helium density is $\rho_{He}=125\, {\rm kg/}{{\rm m}}^{{\rm 3}}$.
(a) What volume of liquid helium boils away through the venting valve in one hour?
(b) If instead absorbing part of the liquid helium container is aluminized, how much helium boils off in one hour? The emissivity of aluminum is $\epsilon_{Al}=0.1$
(a) Since there is a vacuum between container and shield, so the heat must be transferred through the valve via radiation. Recall that Stefan-Boltzmann law states that the power radiated by an object with absolute temperature $T$ is given by $P_r=e\sigma AT^4$, where $\sigma$ is the Stefan's constant and $e$ is emissivity of the radiating surface. The net heat absorbed by the helium is
\begin{align*} P_{net}=\frac{Q_{abs}}{t}=e\sigma A\left(T^4_{shield}-T^4_{He}\right)\\ \Rightarrow Q_{abs}=4\pi r^2e\,t\sigma\left(T^4_{shield}-T^4_{He}\right) \end{align*} \begin{align*} Q_{abs}&=4\pi{\left(0.1\right)}^2(1)(60\times 60)(5.67\times {10}^{-8})({77}^4-{\left(4.2\right)}^4)\\ &=901.68\ {\rm J} \end{align*} This absorbed heat causes $m\, {\rm g}$ helium boils away through valve so \begin{align*}Q_{abs}&=mL_V\\ \\ \Rightarrow m&=\frac{901.68}{21000}\\ \\&=0.042\ {\rm kg}\end{align*} Use the formulae of density to determine the desired volume. \[V=\frac{m}{\rho}=3.43\times {10}^{-4}\, {\rm m^3}\]
MOST USEFUL FORMULA IN FLUIDS:
Density of a substance:
\[\rho=\frac m v\]
Pressure in a fluid:
\[P=\frac F A\]
Pressure in a static liquid:
\[P=P_0+\rho gh\]
SI unit of pressure:
\[1\,\rm {Pa}=1\, \rm {N/m^2}\]
Common units of pressure:
\begin{align*} 1\,\rm {atm}&=101.325\,\mathrm {kPa}=760\,\mathrm {mmHg}=760\,\mathrm {torr} \\ &\approx 14.70\,\mathrm {lb/in^2} \end{align*}
Bernoulli equation:
\[P+\rho gh+\frac 1 2 \rho v^2= constant\]
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
