Faraday's Law Equation with Simple Solved Examples
Experiments showed that when the magnetic flux through a surface bounded by a wire change, an emf (voltage) is generated in the wire equal to the rate of change of the magnetic flux.
With a simple setup, we can demonstrate Faraday's law formula:
1) Grasp a magnet and move it toward a stationary conducting ring of wire which is connected to the ammeter. The ammeter shows a deflection.
2) Now move the magnet away from the ring. Again, the ammeter shows a deflection but in a reverse direction.
3) In the third case, both the magnet and the ring are stationary. The ammeter doesn't show any deflection.
4) Now suppose the magnet is fixed and the loop is moving toward or away from the magnet. Result: ammeter reads a current!
This simple observation shows that a current is induced in a wire loop when a magnet or a loop moves toward or away from one another.
In other words, a current is induced (produced) in a closed conducting path when there is a relative motion between the magnet and the closed path. This current is produced by an induced emf.
All the above words can be summarized as follows:
If the magnetic flux through a loop changes with time then an emf(voltage) is induced around the loop. The average induced emf is \[\mathcal{E}=-\frac{\Delta \Phi_m}{\Delta t}\]This is Faraday's law of induction.
The minus sign in Faraday's law equation is related to the direction of the induced emf.
Key notes about Faraday's law of induction:
(1) an emf is induced in a closed loop or any other closed conducting circuit as long as there is a changing magnetic flux.
(2) magnetic flux in the above equation is the total flux through the closed loop. If a coil has $N$ tightly wound loops, then $\Phi_m=N\phi_m$ where $\phi_m$ is the flux through each loop of the coil.
(3) The direction of the induced emf or induced current is obtained using Lenz's law or directly with the direction of the normal vector to the loop.
Faraday's Law of Induction Solved Problems
Now we want to solve some problems to see Faraday's law equation in action:
Example (1): A loop of area $200\,{\rm cm^2}$ is positioned perpendicular to a uniform magnetic field. Without changing in direction of the magnetic field, its magnitude is reduced by $0.08\,{\rm T}$ in the time interval $0.02\,{\rm s}$. Find the average induced emf in the loop.
Solution: according to Faraday's law of induction equation, a changing magnetic flux through a closed surface bounded by a wire, creates an emf with a magnitude of $\mathcal{E}=|\frac{\Delta \Phi_m}{\Delta t}|$.
Recall that the flux through a surface of area $A$ is defined as $\Phi_m=\vec{B}\cdot\hat{n}A$ where $\hat{n}$ is a unit vector (a vector whose its magnitude is unity) normal (perpendicular) to that surface.
In this example, the area and its direction are fixed so the only factor changes is the magnitude of the magnetic field. Consequently, the change in the flux is written as below \begin{align*}\Delta \Phi_m&=A\Delta B\\&=\left(200\times 10^{-4}\right)(-0.08)\\&=-16\times 10^{-4}\quad {\rm Wb}\end{align*} Next, use Faraday's law formula to find the magnitude of the average induced emf \begin{align*}\mathcal{E}&=\left|\frac{\Delta \Phi_m}{\Delta t}\right|\\ \\ &=\left|\frac{-16\times 10^{-4}}{0.02}\right|\\ \\&=0.08\quad {\rm V}\end{align*}
Example (2): A wire loop of area $A=0.12\,{\rm m^2}$ is placed in a uniform magnetic field of strength $B=0.2\,{\rm T}$ so that the plane of the loop is perpendicular to the field. After $2\,{\rm s}$, the magnetic field reverses its direction. Find the magnitude of the average emf induced in the loop during this time.
Solution: According to Faraday's law, a changing magnetic flux produces an emf in a closed path or circuit.
On the other hand, magnetic flux is also the product of the magnetic field, area, and cosine of the angle between $\vec{B}$ and a unit vector normal to the plane.
In this example, the first two factors are fixed ($B$ and $A$) but the direction of the magnetic field is changed. Thus, if we consider initially the field and the normal to the plane was parallel ($\theta=0^\circ$) then after 2 seconds, they are in opposite direction ($\theta=180^\circ$). Therefore, the change in magnetic flux is as follows \begin{align*} \Delta \Phi_m&=\Phi_2-\Phi_1\\&=BA(\cos \theta_2-\cos\theta_1)\\&=(0.2)(0.12)(\cos 180^\circ-\cos 0^\circ)\\&=0.24(-1-1)\\&=-0.48\quad {\rm Wb}\end{align*} Now applying Faraday's law of induction equation, we can find the magnitude of the induced emf in the loop \begin{align*} \mathcal{E}&=\left|\frac{\Delta \Phi_m}{\Delta t}\right|\\ \\&=\left|\frac{-0.48}{2}\right|\\ \\&=0.24\quad {\rm V}\end{align*}
Example (3): The plane of a 400-turn square coil of side length $40\,{\rm cm}$ makes an angle of $60^\circ$ with a uniform magnetic field. The magnitude of the magnetic field changes with time as $8\,{\rm \frac{T}{s}}$ while its direction is held fixed. What is the magnitude of the induced emf in the coil?
Solution: The magnitude of the induced emf(voltage) is given by Faraday's law equation as \[\mathcal{E}=\left|\frac{\Delta \Phi_m}{\Delta t}\right|\]Here, of three factors involving in the magnetic flux formula ($\Phi_m=BA\cos\theta$), only the magnetic field's magnitude $B$ is changing with time so by inserting it into the above formula we get \begin{align*} \mathcal{E}&=\left|\frac{\Delta \Phi_m}{\Delta t}\right|\\ \\&=\left|\frac{\Delta (BA\cos \theta)}{\Delta t}\right|\\\\&=\left|\left(\frac{\Delta B}{\Delta t}\right)A\cos \theta\right|\\\\&=(8)(0.4\times 0.4)\cos 60^\circ\\ \\&=0.64\quad {\rm V}\end{align*} This is the induced emf in a single turn of a $N$-turn coil.
Total induced emf is equal to the number of turns $N$ times the emf induced in each turns as $\mathcal{E}_t=N\mathcal{E}$ thus, we get \[\mathcal{E}_t=400 \times 0.64=256\quad {\rm V}\]
Example (4): A circular coil with 100 turns and radius $r=10\,{\rm cm}$ and resistance $10\,{\rm \Omega}$ is placed in a uniform magnetic field so that it is perpendicular to the plane of the coil. The field changes uniformly from zero to $0.4\,{\rm T}$ in 2 seconds.
(a) Calculate the induced emf in the coil during the field changing.
(b) How many amps of induced current are established in the coil during that change of field?
Solution: The area of circular loop is \[A=\pi r^2=\pi (0.1)^2=0.01\pi\,{\rm m^2}\] Initial flux through the coil is zero since $B_i=0$. The flux at time $t=2\,{\rm s}$ is obtained as \begin{align*}\Phi_{m,f}&=BA\cos \theta \\&=(0.4)(0.01\pi)\cos 0^\circ\\&=4\pi\times 10^{-3}\quad {\rm Wb}\end{align*}Thus, the change in flux through one turn of the coil is \[\Delta \Phi_m=\Phi_{m,f}-\Phi_{m,i}=4\pi\times 10^{-3}\quad {\rm Wb}\]
(a) Now, put it into Faraday's law formula to find the emf induced in each turn as \begin{align*} \mathcal{E}&=\left|\frac{\Delta \Phi_m}{\Delta t}\right|\\ \\ &=\left|\frac{4\pi\times 10^{-3}\,{\rm Wb}}{0.2\,{\rm s}}\right|\\ \\&=0.2\pi\quad {\rm mV}\end{align*} Consequently, the total emf induced in the coil is \begin{align*} \mathcal{E}_t&=N\mathcal{E}\\&=100\times (0.2\pi\times 10^{-3})\\&=0.02\pi \quad{\rm V}\end{align*}
(b) The magnitude of the induced current is obtained as \[I=\frac{|\mathcal{E}_t|}{R}\] Thus, in this problem we have \[I=\frac{0.02\pi}{10}=2\pi\quad {\rm mA}\]
Example (5): A solenoid with length of $L=25\,{\rm cm}$ has a radius of $r=4\,{\rm cm}$ and $500$ turns. It is placed in a region where a uniform magnetic field of magnitude $400$ gauss makes an angle of $37^\circ$ with the axis of the solenoid. Find the average induced emf if the magnetic field finally is reduced to zero in $0.2\,{\rm s}$.
Solution: first of all collect and convert all data into SI units as below \begin{gather*} \theta=37^\circ \\ \Delta t=0.2\,{\rm s}\\L=25\,{\rm cm}=0.25\,{\rm m} \\ r=4\,{\rm cm}=0.04\,{\rm m} \\A= \pi r^{2} \\ B_i=400\,{\rm G}=400\times 10^{-4}=0.04\,{\rm T} \\B_f=0 \end{gather*} Since the only changing parameter is the magnetic field $B$ so the change in magnetic flux through each turn of the solenoid is obtained as \begin{align*}\Delta\phi_m&=(B_f-B_i)A\cos \theta\\&=(0-0.04)\pi(0.04)^{2}\cos 37^\circ\\&=5.1\times 10^{-5}\quad {\rm Wb}\end{align*} The change in total flux through the coil is \[\Delta \Phi_m=N\phi_1=0.02\]The amount of induced emf is obtained using Faraday's law formula as following \begin{align*}\mathcal{E}&=-\frac{\Delta \Phi_m}{\Delta t}\\\\&=-\frac{0.02}{0.2}\\\\&=-0.1\quad {\rm V}\end{align*} The minus sign shows the direction of the emf induced in the solenoid.
Problem (6): A solenoid is being pulled away from a loop as shown in the figure below. What is the direction of the current induced in the loop?
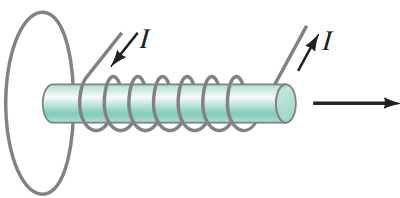
Solution: If we put our thumb along the direction of the current in the wire, our turned fingers show the direction of the magnetic field inside the solenoid, which is to the right. By pulling the solenoid away from the loop, the number of magnetic field lines crossing the area of the loop, called magnetic flux, is decreasing. This changing magnetic flux induces an emf in the loop, according to Faraday's law of induction.
The direction of this induced current is found using Lenz's law. According to this law, the direction of the induced current is so that the magnetic field created by that current opposes any initial changes in the magnetic flux.
Here, we must set up a current in the loop so that its associated magnetic field compensated for the increasing or decreasing flux through the desired surface.
In this case, the magnetic flux or number of field lines through the loop is decreasing, so the current in the coil must be in a direction that compensates for this decrease.
A counterclockwise current circling in the loop creates a magnetic field pointing to the right.
A clockwise current in the loop produces a magnetic field pointing to the left and cancels the effect of the original decreasing flux due to the movement of the solenoid away from the loop.
As a result, a clockwise current is induced in the loop.
Problem (7): A flexible loop of radius $15\,\rm cm$ is located perpendicularly inside an external magnetic field of strength $0.25\,\rm T$. We hold the loop from points $A$ and $B$ and stretch it until its area nearly becomes zero in $0.5\,\rm s$. In this time interval, how much average emf is induced in the loop?
Solution: Initially the lines of the external magnetic field are crossing the whole area enclosed by the loop at a right angle, $\theta=0^\circ$.
In this stage, the amount of flux is determined as \begin{align*} \Phi_i&=BA\cos\theta \\\\&=(0.25)(0.15) \cos 0^\circ \\\\ &=0.0375\quad\rm T\cdot m^2\end{align*} After the loop is completely stretched, its area is nearly zero and consequently, there is no longer magnetic flux through it, giving $\Phi_f=0$.
During this process, the flux passing through the loop is changed, and according to Faraday's law of induction, an emf is produced along the loop whose magnitude is given by \[\mathcal E=-\frac{\Delta \Phi_B}{\Delta t}\] Therefore, the average magnitude of the induced emf during the $0.5-\rm s$ time interval is \begin{align*} \mathcal E&=\frac{\Delta \Phi_B}{\Delta t} \\\\ &=\frac{(0-0.0375) \,\rm T\cdot m^2}{0.5\,\rm s} \\\\ &=0.075\,\rm V\end{align*} Keep in mind that the minus sign in the above formula gets the direction of the induced emf in the loop.
For more solved examples, go here.
Date Published: 2/19/2021
Author: Dr. Ali Nemati
© 2015 All rights reserved. by Physexams.com