Physics Work Problems for High Schools
In this tutorial, we want to practice some problems on work in physics. All these questions are easy and helpful for your high school homework.
Work Problems: Constant Force
Problem (1): A constant force of 1200 N is required to push a car along a straight line. A person displaces the car by 45 m. How much work is done by the person?
Solution: If a constant force $F$ acts on an object over a distance of $d$, and $F$ is parallel to $d$, then the work done by force $F$ is the product of the force times distance.
In this case, a force of $1200\,{\rm N}$ displaces the car $45\,{\rm m}$. The pushing force is parallel to the displacement. So, the work done by the person is equal to \[W=Fd=1200\times 45=54000\,{\rm J}\] The SI unit of work is the joule, ${\rm J}$.
Problem (2): You lift a book of mass $2\,{\rm kg}$ at constant speed straight upward a distance of $2\,{\rm m}$. How much work is done during this lifting by you?
Solution: The force you apply to lift the book must be balanced with the book's weight. So, the exerted force on the book is \[F=mg=2\times 10=20\quad{\rm N}\] The book is lifted 2 meters vertically. The force and displacement are both parallel to each other, so the work done by the person is the product of them. \[W=Fd=20\times 2=40\quad {\rm J}\]
Problem (3): A force of $F=20\,{\rm N}$ at an angle of $37^\circ$ is applied to a 3-kg object initially at rest. The object has displaced a distance of $25\,{\rm m}$ over a frictionless horizontal table. Determine the work done by
(a) The applied force
(b) The normal force exerted by the table
(c) The force of gravity
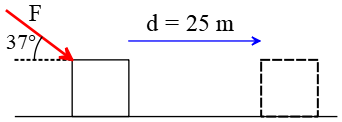
Solution: In this problem, the force makes an angle with the displacement. In such cases, we should use the work formula $W=Fd\cos\theta$ where $\theta$ is the angle between force $F$ and displacement. To this object, an external force $F$, normal force $F_N$, and a gravity force $w=mg$ are applied.
(a) Using vector decompositions, the component of the force parallel to the displacement is found to be $F_{\parallel}=F\cos \theta$. Thus, the product of this component parallel to the displacement times the magnitude of displacement gives us the work done by external force $F$ as below \begin{align*} W_F&=\underbrace{F\cos\theta}_{F_{\parallel}}d\\\\ &=(20\times \cos 37^\circ)(25)\\\\&=400\quad {\rm J}\end{align*}
(b) Now, we want to find the work done by the normal force. But let's define what the normal force is.
In physics, ''normal'' means perpendicular. When an object is in contact with a surface, a contact force is exerted on the object. The component of the contact force perpendicular to the surface is called the normal force.
Thus, by definition, the normal force is always perpendicular to the displacement. So, the angle between $F_N$ and displacement $d$ is $90^\circ$. Hence, the work done by the normal force is determined to be \[W_N=F_N d\cos\theta=(30)(25)\cos 90^\circ=0\]
(c) The weight of the object is the same as the force of gravity. This force applies to the object vertically downward, and the displacement of the object is horizontal. So, again, the angle between these two vectors is $\theta=90^\circ$. Hence, the work done by the force of gravity is zero.
Problem (4): A person pulls a crate using a force of $56\,{\rm N}$ which makes an angle of $25^\circ$ with the horizontal. The floor is frictionless. How much work does he do in pulling the crate over a horizontal distance of $200\,{\rm m}$?
Solution: The component of the external force parallel to the displacement does work on an object over a distance of $d$. In all work problems in physics, this force component parallel to the displacement is found by the formula $F_{\parallel}=F\cos \theta$. Thus, the work done by this force is computed as below \begin{align*} W&=F_{\parallel}d\\&=(F\cos\theta)d\\&=(56\cos 25^\circ)(200) \\&=10080\quad {\rm J}\end{align*} We could use the work formula from the beginning $W=Fd\cos\theta$ where $\theta$ is the angle between $F$ and $d$.
Problem (5): A worker pushes a cart with a force of $45\,{\rm N}$ directed at an angle of $32^\circ$ below the horizontal. The cart moves at a constant speed.
(a) Find the work done by the worker as the cart moves a straight distance of $50\,{\rm m}$.
(b) What is the net work done on the cart?
Solution:(a) All information to find the work done by the worker is given, so we have \begin{align*} W&=Fd\cos\theta\\&=(45)(50) \cos 32^\circ\\&=1912.5\quad {\rm J}\end{align*}
(b) ''net'' means "total". In all work problems in physics, there are two equivalent methods to find the net work. Identify all forces that are applied to the cart, find their resultant force, and then compute the work done by this net force over a specific distance.
Or compute all works done on the object across a distance individually, then sum them algebraically.
Usually, the second method is easier. We take this approach here.
The cart moves in a straight horizontal path. All forces apply on it are, the worker force $F$, the normal force $F_N$, and the force of gravity or its weight $F_g=mg$. The work done by normal and gravity forces in a horizontal displacement is always zero since the angle between these forces and the displacement is $90^\circ$. So, $W_N=W_g=0$. Hence, the net (total) work done on the object is \[W_{total}=W_N+W_g+W_F=1912.5\,{\rm J}\]
Problem (6): A $1200-{\rm kg}$ box is at rest on a rough floor. How much work is required to move it $5\,{\rm m}$ at a constant speed (a) along the floor against a $230\,{\rm N}$ friction force, (b) vertically?
Solution: In this problem, we want to displace a box $5\,{\rm m}$ horizontally and vertically. In the horizontal direction, there is also kinetic friction.
(a) At constant speed, means there is no acceleration in the course of displacement, so according to Newton's second law $\Sigma F=ma$, the net force on the box must be zero. To meet this condition, the external force $F_p$ applied by a person must cancel out the friction force $f_k$. So, \[F_p=f_k=230\quad {\rm N}\] The force $F_p$ and displacement are both parallel, so their product get the work done by $F_p$ \[W_p=F_p d=230\times 5=1150\quad {\rm J}\]
(b) In the vertical path, two forces act on the box. One is the external lifting force, and the other is the force of gravity. Since the box is moving at constant speed vertically, there is no acceleration, and thus this lifting external force $F_p$ must be balanced with the weight of the box. \[F_p=F_g=mg=(1200)(10)=12000\,{\rm J}\] Assume the box is moved vertically upward. In this case, the lifting force and displacement are parallel, so the angle between them is zero $\theta=0$, and the work done by this force is \[W_p=F_p d\cos 0=12000\times 5=60\,{\rm kJ}\] On the other side, the weight force, or force of gravity $F_g=mg$ is always downward, so the angle between the box's weight and upward displacement is $180^\circ$. So, the work done by the weight of the box is \begin{align*}W_g&=F_g d\cos 180^\circ \\\\ &=(1200)(10)(5)(-1) \\\\ &=-60\,{\rm kJ}\end{align*} In such cases where the angle between $F$ and $d$ is $180^\circ$, they are called antiparallel.
Problem (7): A 40-kg crate is pushed using a force of 150 N at a distance of $6\,{\rm m}$ on a rough surface. The crate moves at a constant speed. Find (a) the work done by the external force on the crate.
(b) The coefficient of kinetic friction between the crate and the floor?
Solution: (a) the crate is moved horizontally through a distance of $6\,{\rm m}$ by a force parallel to its displacement. So, the work done by this external force is \[W_p=F_p d \cos\theta=(150)(6)\cos 0=900\,{\rm J}\] where subscript $p$ denotes the person or any external agent.
(b) According to the definition of the kinetic friction force formula, $f_k=\mu_k F_N$, to find the coefficient of kinetic friction $\mu_k$, we must have both the friction force and normal force $F_N$.
In the question, we are told that the crate moves at a constant speed, so there is no acceleration, and thus, the net force applied to it must be zero.
When the friction force, which opposes the motion, is equal to the external force $F_p$, then this condition is satisfied. So, \[f_k=F_p=150\,{\rm N}\] On the other side, the crate is not lifted off the floor, so there is no motion vertically.
Balancing all forces applied vertically, the weight force and the normal force $F_N$, we can find the normal force $F_N$ as below \begin{gather*} F_N-F_g=0\\ F_N=F_g\\ \Rightarrow F_N=mg=40\times 10=400\quad {\rm N}\end{gather*} Therefore, the coefficient of kinetic friction is found to be \[f_k=\frac{f_k}{F_N}=\frac{150}{400}=0.375\]
Practice these questions to understand friction force
Problems on the coefficient of friction
Problem (8): A 18-kg packing box is pulled at constant speed by a rope inclined at $20^\circ$. The box moves a distance of 20 m over a rough horizontal surface. Assume the coefficient of kinetic friction between the box and the surface to be $0.5$.
(a) Find the tension in the rope?
(b) How much work is done by the rope on the box?
Solution: The aim of this problem is to find the work done by the tension in the rope. The magnitude of the tension in the rope is not given. So, we must first find it.
(a) We are told the box moves at a constant speed, so, as previously mentioned, the net force on the box must be zero to produce no acceleration. But what forces are acting horizontally on the box? The horizontal component of tension in the rope, $T_{\parallel}=T\cos\theta$, and the kinetic friction force $f_k$ in the opposite direction of motion are the forces acting on the box horizontally.
If these two forces are equal in magnitude but opposite in direction, then their resultant (net) becomes zero, and consequently, the box will move at a constant speed. \begin{align*} f_k&=T_{\parallel}\\\mu_k F_N&=T\cos\theta\quad (I) \end{align*} The forces in the vertical direction must also cancel each other since there is no motion vertically. As you can see in the figure, we have \[F_N=T\sin\theta+F_g\] Substituting this into the relation (I), rearranging and solving for $T$, yields \begin{gather*} \mu_k (T\sin\theta+mg)=T\cos\theta \\\\ \Rightarrow T=\frac{\mu_k mg}{\cos\theta-\mu_k\sin\theta}\end{gather*} Substituting the numerical values into the above expression, we find the tension in the rope. \[T=\frac{(0.5)(18)(10)}{\cos 20^\circ-(0.5) \sin20^\circ}=117\quad {\rm N}\]
(b) The only force that causes the box to move some distance is the horizontal component of the tension in the rope, $T_{\parallel}=T\cos\theta$. So, the work done by the tension in the rope is \begin{align*} W&=T_{\parallel}d\\ &=(117)( \cos 20^\circ)(20) \\&=2199\quad {\rm J}\end{align*}
Problem (9): A table of mass 40 kg is accelerated from rest at a constant rate of $2\,{\rm m/s^2}$ for $4\,{\rm s}$ by a constant force. What is the net work done on the table?
Solution: This is a combination of a kinematics problem and a physics work problem. Here, first, we must find the distance over which the box is displaced. The given information is: initial speed $v_0=0$, acceleration $2\,{\rm m/s^2}$, time taken $t=4\,{\rm s}$. Using this data, we can find the total displacement by applying the kinematics equation $\Delta x=\frac 12 at^2+v_0t$, \begin{align*} \Delta x&=\frac 12 at^2+v_0t\\\\&=\frac 12 (2)(4)^2+0(4)\\\\&=16\quad {\rm m}\end{align*} So, this constant force causes the table to move a distance of 16 meters across the surface. To find the work done, we need a force, as well. The force is mass times acceleration, $F=ma$, so we have \[F=ma=40\times 2=80\,{\rm N}\] Now that we have both the force and displacement, the net work done on the table is the product of force along the displacement times the magnitude of displacement \[W=80\times 16=128\quad {\rm J}\]
Work problems in a uniform circular motion
Problem (10): A 5-kg object is held at the end of a string and undergoes uniform circular motion around a circle of radius $5\,{\rm m}$. If the tangential speed of the object around the circle is $15\,{\rm m/s}$, how much work was done on the object by the centripetal force?
Solution: Here, an object moves around a circle, so we encounter a uniform circular motion problem.
In such motions around a curve or circle, that force in the radial direction exerting on the object is called the centripetal force.
On the other hand, a movement around a circle is tangent to the path at any instant of time. Thus, we conclude that in any uniform circular motion, a force is applied to the whirling object that is perpendicular to its motion at any moment of time.
So, the angle between the centripetal force and displacement at any instant is always zero, $\theta=0$. Using the work formula $W=Fd\cos\theta$, we find that the work done by the centripetal force is always zero.
This is another example of zero work in physics.
Work problems on an incline
Problem (11): A $5-{\rm kg}$ box, initially at rest, slides $2.5\,{\rm m}$ down a ramp of angle $30^\circ$. The coefficient of friction between the box and the incline is $\mu_k=0.435$. Determine (a) the work done by the gravity force, (b) the work done by the frictional force, and (c) the work done by the normal force exerted by the surface.
Solution: This part is related to problems on inclined plane surfaces. The forces acting on a box on an inclined plane are shown in the figure. As you can see, the forces along the direction of motion are the parallel component of the weight $W_{\parallel}$, and the friction force $f_k$.
(a) In the figure, you realize that the angle between the object's weight (the same as the force of gravity) and downward displacement $d$ is zero, $\theta=30^\circ$.
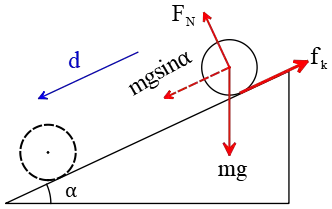
So, the work done by the force of gravity on the box is found using work formula as below \begin{align*} W&=Fd\cos\theta\\&=(mg)(d) \cos 30^\circ\\&=(5\times 10)(2.5) \cos 30^\circ\\&=108.25\quad {\rm J}\end{align*}
(b) To find the work done by friction, we need to know its magnitude. From the kinetic friction force formula, $f_k=\mu_k F_N$, we must determine, first, the normal force acting on the box.
There is no motion in the direction perpendicular to the incline, so the resultant of forces acting in this direction must be zero. Equating the same direction forces, we will have \[F_N=mg\sin\alpha=(5)(10) \sin 30^\circ=25\,{\rm N}\] Substituting this into the above equation for kinetic friction, we can find its magnitude as \[f_k=\mu_k F_N=(0.435)(25)=10.875\,{\rm N}\] The friction force and the displacement of the box down the ramp are parallel, i.e., $\theta=0$. The work done by friction is \begin{align*} W_f&=f_kd\cos\theta \\\\ &=(10.875)(2.5) \cos 0\\\\ &=27.1875\,{\rm J}\end{align*}
(c) By definition, the normal force is the same contact force that is applied to the object from the surface perpendicularly. On the other hand, the object moves along the incline, so its displacement is perpendicular to the normal force, $\theta=90^\circ$. Hence, the work done by the normal force is zero. \[W_N=F_N d\cos\theta=F_N d\cos 90^\circ=0\]
Problem (12): We want to push a $950-{\rm kg}$ heavy object 650 m up along a $7^\circ$ incline at a constant speed. How much work do we do over this distance? Ignore friction.
Solution: When it comes to constant speed in all work problems in physics, you must remember that all forces in the same direction must be equal to the opposing forces. This condition ensures that there is no acceleration in the motion.
In this case, all forces acting on the object are: the pushing force along the incline upward $F_p$, and the parallel component of the force of gravity (weight) along the incline downward, $W_{\parallel}=mg\sin\alpha$. Thus, we can find the pushing force as \begin{align*}F_p&=mg\sin 7^\circ\\\\ &=(950)(10) \sin 7^\circ \\\\& =1159\quad {\rm N}\end{align*} In the question, we are told that the object is moving up the incline, so the angle between its displacement and upward pushing force is zero, $\theta=0$. Hence, the work done by the person to push the object along the incline upward is \begin{align*} W_p&=F_p d\cos\theta\\&=1159\times 650 \cos 0\\&=753350\quad{\rm J}\end{align*}
Problem (13): Consider an electron moving at a constant speed of $1.1\times 10^6\,\rm m/s$ in a straight line. How much energy is required to stop this electron? (Take the electron's mass, $m_e=9.11\times 10^{-31}\,\rm kg$.
Solution: In this problem on work, we cannot use the work formula directly, since none of the work variables, i.e., $F$, $d$, $\theta$, are given except the velocity. In these cases, we have a problem on the work-energy theorem.
According to this rule, the net work done over a distance by a constant force on an object of mass $m$ equals the change in its kinetic energy \[W_{net}=\underbrace{\frac 12 mv_f^2-\frac 12 mv_i^2}_{\Delta K}\] Substituting the numerical values given in this problem, we get the required work to stop this fast-moving electron. \begin{align*}W_{net}&=\frac 12 m(v_f^2-v_i^2) \\\\ &=\frac 12 (9.11\times 10^{-31}) \left(0^2-(1.1\times 10^6)^2 \right) \\\\ &=-5.5\times 10^{-19}\,\rm J\end{align*} where we set the final velocity $v_f=0$ since the electron is to stop.
Problem (14): How much power is needed to lift a $25-\rm kg$ weight $1\,\rm m$ in $1\,\rm s$?
Solution: The power in physics is defined as the ratio of work done on an object to the time taken $P=\frac{W}{t}$. The SI unit of power is the watt ($W$).
In this problem, first, we must find the amount of work done in lifting the object as much as $1,\rm m$ vertically. The only force involved in this situation is the downward weight force. Thus, \[W=(mg)h=(25\times 10)(1)=250\,{\rm J}\] This amount of work has been done in a time interval of $1\,\rm s$. Hence, the power is calculated as below \[P=\frac{W}{t}=\frac{250}{1}=250\,\rm W\]
Problem (15): A particle having charge $-3.6\,\rm nC$ is released from rest in a uniform electric field $E$ moves a distance of $5\,\rm cm$ through it. The electric potential difference between those two points is $\Delta V=+400\,\rm V$. What work was done by the electric force on the particle?
Solution: The work done by the electric force on a charged particle is calculated by $W_E=qEd$, where $E$ is the magnitude of the electric field and $d$ is the amount of distance traveled through $E$. But in this case, the electric field strength is not given, and we cannot use this formula.
We can see this as a problem on electric potential. Recall that the work done by the electric force on a charge to move it between two points with different potentials is given by $W=-q\Delta V$. Substituting the given numerical values into this, we will have \begin{align*} W&=-q\Delta V \\&=-(-3.6)(+400) \\&=\boxed{1440\,\rm J} \end{align*}
Summary:
Here, we learned how to calculate the work done by a constant force in physics by solving a couple of example problems.
Overall, the work done by a constant force is the product of the horizontal component of the force times the displacement between the initial and final points.
In addition, power, a related quantity to work in physics, is also defined as the rate at which work is done.
Author: Dr. Ali Nemati
Date Published: 9/20/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
