Electrostatics practice problems: AP Physics 1
In this long article, we are going to solve some problems on the electrostatic force due to some point charges. All these practice questions are helpful for the AP Physics C prep and college final exams.
Electrostatics Practice Problems
Problem (1): In an experiment, some excess electrons are placed on a $4-\rm g$ small gold sphere, resulting in its net charge becoming $-6.4\,\rm nC$.
(a) How many excess electrons are there on the sphere?
(b) Find the number of excess electrons per gold atom.
(The atomic number and atomic mass of gold are $79$, $197\,\rm g/mol$, respectively.)
Solution: All objects are naturally neutral, meaning they have no any excess charge. When some extra charge is delivered to an initially neutral object, it is negatively or positively charged as much as $Q$.
This charge is related to the number of transferred electrons or protons, $n$ by \[Q=ne\] where $e$ is the fundamental charge of an electron, $1.6\times 10^{-19}\,\rm C$.
(a) The total number $n$ of transferred extra electrons charged the gold sphere as much as $q=-6.4\,\rm nC$. Thus, according to the above formula, this amount of charge corresponds to the following number of electrons \begin{align*} n&=\frac{q}{e}\\\\&=\frac{-6.4\times 10^{-9}}{-1.6\times 10^{-19}} \\\\ &=\boxed{4\times 10^{10}}\end{align*}
(b) First, determine how many moles equal $4\,\rm g$ of gold. The atomic mass of gold tells us that one mole of gold has $197\,\rm g$ of mass. On the other hand, there are $6.02\times 10^{23}$ atoms in one mole of any element.
A simple proportion gives us the number of atoms in the gold sphere \begin{align*} N&=\frac{4\,\rm g}{197\,\rm g}\times (6.02\times 10^{23}) \\\\ &=1.22\quad\rm atoms\end{align*} Therefore, the excess electrons per gold atom are found to be \begin{align*} \frac{n}{N}&=\frac{4\times 10^{10}}{1.22\times 10^{22}} \\\\ &=3.2\times 10^{-12}\end{align*}
Problem (2): A plastic ruler is rubbed with a cloth; as a result, it acquires a charge of $-3.4\times 10^{-8}\,\rm C$. Does the mass of the rod increase or decrease, and by how much?
Solution: Once two initially neutral objects are rubbed together, the electrons are removed from one object and transferred to the other. As a result, the object loses its electrons and is converted into a positively charged object, while the other object, which gains the same number of electrons, ends up with a negatively charged object.
The number of transferred electrons between the two objects is related to the object's net electric charge, $q$, and the fundamental charge $e$ as below \[q=\pm ne\] where the plus sign is for when the object loses electrons and the negative for gaining electrons.
Here, the final charge of the plastic ruler after rubbing is negative, $q=-3.4\times 10^{-8}\,\rm C$, so in this process, it gains some extra electrons, whose number is determined by solving for $n$ from the above formula and substituting the numerically given values into it \begin{align*} n&=-\frac{q}{e} \\\\ &=-\frac{-3.4\times 10^{-8}}{1.6\times 10^{-19}} \\\\ &=\boxed{1.125\times 10^{11}} \end{align*} This is the number of electrons that caused the plastic ruler to become negatively charged when rubbed with the cloth.
Remember that each electron has a mass of $m_e=9.109\times 10^{-31}\,\rm kg$. Once such a huge number of electrons are removed from the plastic ruler (or rod), the ruler's mass is slightly reduced by an amount whose value is found as below \begin{gather*} \Delta m=Nm_e\\ =\left(1.125\times 10^{11}\right) \times \left(9.109\times 10^{-31}\right) \\ \Rightarrow \boxed{\Delta m=1.025\times 10^{-19}\,\rm kg} \end{gather*} In the formula above, $\Delta m$ is the amount that the object's mass is changed by gaining or losing electrons in a process of rubbing.
This increase in the object's mass is hugely small compared to the object's original mass.
Refer to the section on the electric charge problems for more practice.
Problem (3): A negative charge of $-0.450\,\rm \mu C$ applies an upward force of $0.250\,\rm N$ to an unknown charge, $0.450\,\rm m$ straight below it.
(a) What is the magnitude and sign of the unknown charge?
(b) What are the magnitude and direction of the unknown charge applied to the charge above it?
Solution: According to Coulomb's law, two charged particles, having charges $q_1$ and $q_2$, at a distance $r$ from each other, exert forces on one another whose magnitude is \[F_{1-on-2}=F_{2-on-1}=k\frac{|q_1||q_2|}{r^2}\] where $k$ is called the Coulomb (or electrostatic) constant.
The second part of this law explains the direction of the electric force. It says that the forces are directed along the line joining the two particles; they are repulsive if the charges have the same sign and attractive if they are unlike. These forces are a pair of actions and reactions.
(a) Applying Coulomb's law formula and solving for the unknown charge $q_x$ gives \begin{align*} q_x&=\frac{Fr^2}{kq_1} \\\\ &=\frac{0.250\times (0.450)^2}{(9\times 10^9)(0.45\times 10^{-6})} \\\\ &=\boxed{12.5\times 10^{-6}\,\rm C}\end{align*} Keep in mind that in Coulomb's law formula, only the absolute values of the charges, without any positive or negative sign, are involved.
Recall that two like charges attract each other and unlike charges repel. By exerting an upward force on the unknown charge, the top charge actually pulls the unknown charge at the bottom towards itself.
The electric forces due to the two point charges applied on each charge are a pair of actions/reactions. That means that the bottom unknown charge should also pull the top charge straight toward itself downward.
This is the case when two electric charges have the opposite sign or are unlike electric charges. As a result, the bottom unknown charge must be positive since the top charge is negative.
(b) We argued in the preceding part that the bottom unknown charge $q_x$ must be a positive charge. On the other hand, according to Coulomb's law, the force magnitude applied to each charge due to the other charge is the same. Therefore, \[F_{q_1-on-q_x}=F_{q_x-on-q_1}=0.250\,\rm N\]
Problem (4): Two small plastic spheres, each having a mass of $0.250\,\rm kg$ and charge of $-60\,\rm nC$, are placed $2\,\rm cm$ apart center-to-center.
(a) What electric force (magnitude and direction) does each sphere exert on the other?
(b) What is the ratio of electric force between the spheres and their weight?
Solution: Two charged objects exert an electric force whose magnitude is obtained using the following Coulomb's law formula, \[F_e=k\frac{|q_1||q_2|}{r^2}\] where $k_e\approx 9\times 10^9\, \rm N\cdot m^2/C^2$ is the Coulomb constant. Notice that $|\cdots|$ means that the value of charges must be inserted, regardless of their signs.
(a) The magnitudes (or strengths) of the electric force that two charged particles apply to each other are the same but are in opposite directions. Applying the above equation and solving for $F_e$ gives us \begin{align*} F_e&=k\frac{|q_1||q_2|}{r^2}\\\\ &=(9\times 10^9) \frac{(60\times 10^{-9})(60\times 10^{-9})}{(0.02)^2} \\\\ &=0.081\,\rm N\end{align*} Note that according to Coulomb's law, the electric force between two charged objects does not depend on the mass of each object.
(b) Weight, $W$, is defined as the product of mass, $m$, and the gravitational acceleration, $g=9.8\,\rm m/s^2$. \[W=mg\] Simply construct the ratio of these two forces to be able to compare them. \begin{align*} \frac{W}{F_e}&=\frac{mg}{F_e} \\\\ &=\frac{0.25\times 9.8}{0.081} \\\\ &=3.025 \end{align*} This tells us that the weight of each sphere is about $3$ times the electric force between the spheres.
Problem (5): Four identical point charges of $4.6\,\rm nC$ are placed at the corners of a $0.30\,\rm cm$-side square. What electric force is applied to each charge?
Solution: The total (or net) electrostatic force on a charge due to an arrangement of other charges is determined by the vector sum of each force exerted on that charge separately. This is called the superposition principle.
First, calculate the magnitude of the electrostatic force applied to one of the charges due to each charge, say the charge located at the right upper corner.

The charges $q_1$ and $q_2$ have the same magnitude and are at the same distance from the desired charge $q_4$. Thus, using Coulomb's law, the magnitude of the applied electric force on $q_4$ is found to be \begin{align*} F_{14}=F_{24}&=k\frac{|q||q'|}{r^2} \\\\ &=k\frac{q^2}{x^2} \end{align*} The magnitude of the electric force that the charge $q_3$ is applied to the charge $q_4$ is written \begin{align*} F_{34}&=k\frac{|q||q'|}{r^2} \\\\ &=k\frac{q^2}{d^2}\\\\&=k\frac{q^2}{x^2+x^2}\end{align*} This force points away from the charge $q_4$ and lies along the line joining $q_3$ to $q_4$. In a situation where there is an arrangement of charges in two dimensions, we have to resolve one of the forces into its $x$ and $y$ components.
In this question, resolve $\vec{F}_{34}$ into its components along the $x$ and $y$ axes, as shown in the figure below.

\begin{align*} F_{34-x}&=F_{34}\cos 45^\circ \\&=F_{34}\times \frac{\sqrt{2}}{2} \\\\ F_{34-y}&=F_{34}\sin 45^\circ \\&=F_{34}\times \frac{\sqrt{2}}{2} \end{align*} where $F_{34}$ is the magnitude of the force vector $\vec{F}_{34}$. The force $\vec{F}_{14}$ is horizontal and points in the positive $x$ direction or in vector notation as \[\vec{F}_{14}=k\frac{q^2}{x^2}\quad (\hat{i})\] Similarly, the force $\vec{F}_{24}$ is directed upward along the positive $y$ direction \[\vec{F}_{24}=k\frac{q^2}{x^2}\quad (\hat{j})\] The next crucial step in solving these questions is adding the forces as vectors. Sum the $x$ and $y$ components separately to find the $x$ and $y$ components of the net electric force applied to the charge $q_4$. \begin{align*} F_{net-x}&=F_{1-x}+F_{2-x}+F_{3-x} \\\\ &=k\frac{q^2}{x^2}+0+k\frac{q^2}{2x^2}\left(\frac{\sqrt{2}}{2}\right) \\\\ &=k\frac{q^2}{x^2} \left(1+\left(\frac{\sqrt{2}}{4}\right)\right) \\\\ F_{net-y}&=F_{1-y}+F_{2-y}+F_{3-y} \\\\ &=0+k\frac{q^2}{x^2}+k\frac{q^2}{2x^2}\left(\frac{\sqrt{2}}{2}\right) \\\\ &=k\frac{q^2}{x^2} \left(1+\left(\frac{\sqrt{2}}{4}\right)\right) \end{align*} Substituting the numerical values into those, we have \begin{gather*} F_{net-x}=k\frac{q^2}{x^2} \\\\ =(9\times 10^9) \times \frac{(4.6\times 10^{-9})^2}{(0.30)^2} \left(1+\left(\frac{\sqrt{2}}{4}\right)\right) \\\\ =\boxed{2.86\times 10^{-6}\,\rm N} \end{gather*} Similarly, \[F_{net-y}=2.86\times 10^{-6}\,\rm N\] The Pythagorean theorem gives us the magnitude of the net force $F_{net}$ applied to the charge $q_4$ \begin{align*}F_{net}&=\sqrt{F_{net-x}^2+F_{net-y}^2} \\\\&=\boxed{4.05\times 10^{-6}\quad \rm N}\end{align*} The angle that net force makes with the horizontal is obtained using the following formula \begin{align*} \theta&=\arctan\left(\frac{F_{net-y}}{F_{net-x}}\right) \\\\ &=\arctan\left(\frac{2.86\times 10^{-6}}{2.86\times 10^{-6}}\right) \\\\ &=\arctan(1) \\\\ \Rightarrow &=\boxed{45^\circ} \end{align*} Therefore, all three other equal-magnitude charges apply a $2.86\,\rm \mu N$ force at an angle of $45^\circ$ to the other charge.
Problem (6): Three identical negative point charges of $4\,\rm \mu C$ have occupied the vertices of an equilateral triangle, $25\,\rm cm$ on a side. Calculate the net electric force on each charge.
Solution: This problem is similar to the previous one, but for practice, the charges have negative signs. We take the net electrostatic force on the charge $q_3$ exerted by other charges.
All charges have the same signs, so there is a repulsive force between any pair of charges.
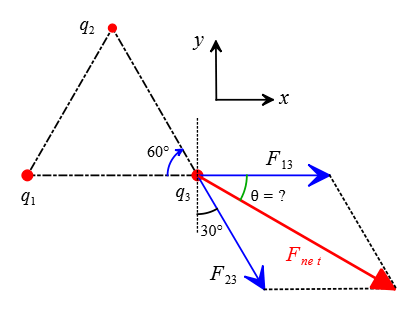
The charge $q_1$ repels $q_3$ away from itself to the right along the positive $x$ axis with a magnitude of \begin{align*} F_{13}&=k\frac{|q_1||q_3|}{a^2} \\\\ &=(9\times 10^9)\times \frac{(4\times 10^{-6})^2}{(0.25)^2} \\\\ &=2.30\quad \rm N\end{align*} In vector notation is \[\vec{F}_{13}=2.30\,\rm (N) \quad \hat{i}\] Similarly, the charge $q_2$ also repels the charge $q_3$ away from itself at an angle of $\alpha=30^\circ$ with the vertical. \begin{align*} F_{13}&=k\frac{|q_2||q_3|}{a^2} \\\\ &=(9\times 10^9)\times \frac{(4\times 10^{-6})^2}{(0.25)^2} \\\\ &=2.30\quad \rm N\end{align*} This force vector must be decomposed into its components along $x$ and $y$ axes. \begin{align*} F_{23-x}&=F_{23}\sin\alpha \\&=2.30\times \sin 30^\circ \\&=1.15\quad \rm N \\\\ F_{23-y}&=F_{23}\cos\alpha \\&=2.304\times \cos 30^\circ \\ &=1.99\quad \rm N\end{align*}
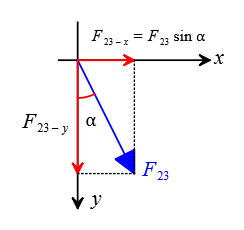
Now perform vector addition by adding axes by axes components together to find the components of the net electrostatic force $F_{net}$ exerted on $q_3$ \begin{align*} F_{net-x}&=F_{13-x}+F_{23-x}\\&=2.30+1.15 \\&=3.45\quad \rm N \\\\ F_{net-y}&=F_{13-y}+F_{23-y}\\&=0+1.99\\&=1.99\quad \rm N\end{align*} The magnitude of the net force is obtained using the Pythagorean theorem \begin{align*} F_{net}&=\sqrt{F_{net-x}^2+F_{net-y}^2} \\&=\sqrt{(3.45)^2+(1.99)^2}\\&=\boxed{3.98\quad\rm N}\end{align*} And it acts at an angle of $\theta$ given by \begin{align*} \theta&=\arctan\left(\frac{F_{net-y}}{F_{net-x}}\right) \\\\ &=\arctan\left(\frac{1.99}{3.45}\right) \\\\ \Rightarrow &\approx\boxed{30^\circ} \end{align*}
Problem (7): Calculate the magnitude and direction of the net electrostatic force on the leftmost charge.
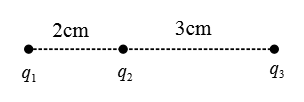
Solution: This electrostatic problem involves three point charges in a line.
According to the superposition principle, the net electrostatic force (Coulomb force) on the charge $q_1$ is the vector sum of the force $\vec{F}_{31}$ exerted by $q_3$ on $q_1$ and the force $\vec{F}_{21}$ exerted by $q_2$ on $q_1$. \[\vec{F}_1=\vec{F}_{31}+\vec{F}_{21}\] This sum is of the vector type, meaning that you must consider the direction of each force. Let the line joining the charges be the $x$-axis, and take it to the right as the positive direction.
The positive charge $q_3$ repels the positive charge $q_1$ straight away from itself to the left. This means that $\vec{F}_{31}$ points in the negative $x$ direction.
Likewise, the positive charge $q_1$ is attracted to the negative charge $q_2$, to the positive $x$ direction, meaning that $\vec{F}_{21}$ points in the positive $x$ direction.
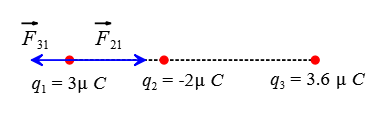
Next, subtract the magnitudes of each electrostatic force due to the charges on the charge $q_1$ as below \begin{gather*} F_1=k\frac{|q_3||q_1|}{r_{31}^2}+k\frac{|q_2||q_1|}{r_{21}^2} \\\\ =(9\times 10^9)(3\times 10^{-6})\left(-\frac{3.6\times 10^{-6}}{(0.05)^2}+\frac{2\times 10^{-6}}{(0.02)^2}\right) \\\\ \Rightarrow \quad \boxed{F_2=+96.12\,\rm N} \end{gather*} where $r_{31}$ is the distance from $q_3$ to $q_1$. The positive sign indicates that the net force exerted on charge $q_1$ due to the other two charges points in the positive $x$ direction with a magnitude of $96.12\,\rm N$.
Problem (8): Two charges of $q_1=1\,\rm nC$ and $q_2=3\,\rm nC$ are spaced $2\,\rm m$ apart. At what point between the charges is the electric field equal to zero?
Solution: Assume a point between the charges where the total electric field is zero, say point $P$ at distance $x$ from the smaller charge $q_1$. Let the line connecting the charges be the $x$ axis, with $q_1$ at the origin, and take it to the right as the positive direction, as shown in the figure below.
Recall that, by definition, the electric field due to a positive point charge is away from it.
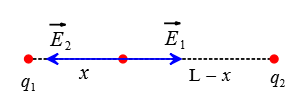
Equate the magnitude of the electric fields due to each charge at point $P$ and solve for the unknown distance $x$. \begin{gather*} E_1=E_3 \\\\ k\frac{|q_1|}{x^2}=k\frac{|q_3|}{(L-x)^2} \\\\ \frac{(1\times 10^{-9})}{x^2}=\frac{(3\times 10^{-9})}{(2-x)^2} \\\\ (2-x)^2=3x^2 \end{gather*} where $L$ is the charge separation. Put the above expression into standard quadratic equation, $ax^2+bx+c=0$, \begin{gather*} (2-x)^2=3x^2 \\ 2+x^2-4x^2=3x^2 \\ \Rightarrow \quad 2x^2+4x-4=0 \end{gather*} Now apply the quadratic formula to solve it \begin{align*} x&=\frac{-4\pm\sqrt{(4)^2-(4)(2)(-4)}}{2(2)} \\\\ &=-1\pm\sqrt{3} \end{align*} The negative root gives us a negative distance, $x=-2.73\,\rm m$, meaning that the point $P$ must be to the left of charge $q_1$, and this violates our initial assumption that the point $P$ is between the charges.
As a result, we choose the plus sign (positive root) since it makes sense. Hence, the correct position where the total electric field is zero is $x_p=0.73\,\rm m$ from the smaller charge.
Problem (9): An electron is moving with a speed of $3.5\,\times 10^6\,\rm m/s$ horizontally to the right.
(a) What is the magnitude and direction of the weakest electric field that can bring it uniformly to rest across a distance of $4.5\,\rm m$?
(b) After entering the field, how much time does it take the electron to completely stop?
Solution: Recall from work-kinetic energy problems that the change in the kinetic energy $\Delta K$ of a moving object over a distance $x$ equals the work done by the external forces $F$ that caused those changes in the velocities (or kinetic energy). \[\Delta K=\frac 12 m(v_f^2-v_i^2)=W_{ext}\] Where $W_{ext}=F_{ext}x$. In this problem, the external electric field applies a force to the charge. Since the electron has a negative charge, it moves in the opposite direction of external $\vec{E}$, unlike the proton, which moves in the direction of $\vec{E}$.
(a) This electron is traveling to the right, so an external electric field directed to the right opposes its motion and finally can bring it to rest. Applying the work-kinetic energy theorem, substituting $F_{ext}=eE_{ext}$ by definition of an electric field, and solving for $E$, we have \begin{gather*} \frac 12 m(v_f^2-v_i^2)=W_{ext}=(eE_{ext})x \\\\ \frac 12 (9.1\times 10^{-31})(0-(3.5\times 10^{6})^2)=(1.6\times 10^{-19})(E_x)(4.5) \\\\ \Rightarrow \boxed{E_{ext}=7.74\quad \rm N/C} \end{gather*}
(b) This part is related to a kinematic problem. Since it's said that the electron's velocity is decreasing uniformly until it comes to a stop, we can use the following kinematic equation. \begin{gather*} \Delta x=\frac{v_f+v_i}{2}\times t \\\\ 4.5=\frac{(3.5\,\times 10^6)+0}{2}\times t \\\\ \Rightarrow \boxed{t=2.6\times 10^{-6}\,\rm s} \end{gather*}
Problem (10): Two point charges of $-8\,\rm \mu C$ and $5.6\,\rm \mu C$ are separated by a distance of $20\,\rm cm$. What is the electric field (magnitude and direction) at a point midway between the charges?
Solution: The free-body diagram for this case is depicted in the figure below.
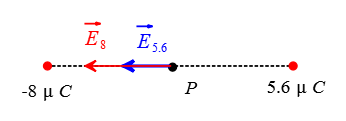
Midway between the two charges, the electric field due to the $-8-\rm \mu C$ charge is directed toward itself with a magnitude of \begin{align*} E_8&=k\frac{|q|}{r^2} \\\\ &=(9\times 10^9) \frac{8\times 10^{-6}}{(0.10)^2} \\\\ &=7.2\times 10^{6}\,\rm N/C\end{align*} Similarly, the electric field due at the midpoint between the charges is directed away from the positive charge $5.6\,\rm \mu C$ and produces a field strength of \begin{align*} E_{5.6}&=k\frac{|q|}{r^2} \\\\ &=(9\times 10^9) \times \frac{5.6\times 10^{-6}}{(0.10)^2} \\\\ &=5.04\times 10^{6}\,\rm N/C\end{align*} At point $P$ we must add the electric fields, but this addition is of the vector type. This type of vector addition in physics is called the superposition principle.
Beware that in calculating the electric field magnitude, we omitted the signs of the charges. But, those signs guided us to find the correct direction of the electric field at a specific point.
Let the line joining the charges be the $x$ axis, and take it positive to the right. We assume that the direction of the electric field due to a positive charge is away from the charge, whereas the field $\vec{E}$ due to a negative charge is toward that charge.
In this electrostatic practice problem, both charges point to the left (i.e., to the negative $x$ axis). Therefore, the total field at point $P$ midway between the charges points to the left and has magnitude \begin{align*} E_{tot}&=E_8+E_{5.6}\\\\ &=(7.2+5.04) \times 10^6 \\\\ &=\boxed{12.24\quad \rm N/C} \end{align*} Or in vector notation is written as \[\vec{E}=12.24\,\rm N/C \quad \left(-\hat{i}\right)\]
Problem (11): What is the magnitude and direction of the electric field due to the given point charges at point $P$ as shown below?
Solution: First, find the electric field magnitude due to each point charge at the desired point as below \begin{align*} E_{-5}&=k\frac{|q|}{x^2} \\\\ &=(9\times 10^9)\times \frac{(5\times 10^{-9})}{(0.03)^2} \\\\&=5\times 10^4 \,\rm N/C \\\\ E_{-10}&=k\frac{|q|}{y^2}\\&=(9\times 10^9) \times \frac{(10\times 10^{-9})}{(0.06)^2} \\\\&=2.5\times 10^4\,\rm N/C \\\\ E_{10}&=k\frac{|q|}{r^2}\\\\ &=(9\times 10^9) \times \frac{(10\times 10^{-9})}{(0.03)^2+(0.06)^2} \\\\&=2\times 10^4 \,\rm N/C \end{align*} Next, sum the electric fields due to each charge separately as vectors. This is the most important and challenging step in solving the electrostatic force problems in any AP Physics C exam.
If the charges were on a line, we could use the plus or minus sign to indicate the direction of each electric field. Here, we encounter a configuration of charges in two-dimension, so it is better to use vector components.
The $-5\,\rm nC$ charge is positioned at the left upper corner, and its electric field at point $P$ is directed toward itself, to the up or $\hat{j}$ or in vector notations \[\vec{E}_{-5}=5\times 10^4\,\rm N/C \quad (\hat{j})\] Similarly, for the charge of $-10\,\rm nC$ at the left bottom corner, we have \[\vec{E}_{-10}=2.5\times 10^4 \,\rm N/C \quad (\hat{i})\] The situation for the $+10\,\rm nC$ charge is a little more difficult. Its electric field direction points away from itself (since it is a positive charge) and lies along the line joining the charge and point $P$ as shown below.
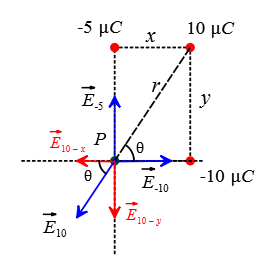
Now, resolve the electric field vector $\vec{E}_{10}$ along $x$ and $y$ axes, which is related to the problem of resolving a vector into its components. \begin{gather*} E_{10-x}=E_{10}\cos\theta \\ E_{10-y}=E_{10}\sin\theta \end{gather*} where $\theta$ is angle that $\vec{E}_{10}$ makes with the horizontal as depicted in the figure. Using the trigonometry functions definition and the geometry, we have \begin{gather*} \cos\theta=\frac yr=\frac{6}{\sqrt{6^2+3^2}}=\frac{6}{\sqrt{45}} \\\\ \sin\theta=\frac xr=\frac{3}{\sqrt{6^2+3^2}}=\frac{3}{\sqrt{45}} \end{gather*} Thus, the components of $\vec{E}_{10}$ are calculated as below \begin{align*} E_{10-x}&=(2\times 10^4) \times \frac{6}{\sqrt{45}}\\&=1.78\times 10^4\,\rm N/C \\\\ E_{10-y}&=(2\times 10^4) \times \frac{3}{\sqrt{45}} \\&=0.89\times 10^4\,\rm N/C \end{align*} Therefore, in vector notation, it is written as \[\vec{E}_{10}=1.78\times 10^4\,(-\hat{i})+0.89\times 10^4 \,(-\hat{j})\] The total (or net) electric field at point $P$ is found using the superposition principle. The sum of $x$ and $y$ components of each electric field separately at point $P$ gives us \begin{align*}E_{P-x}&=E_{-10-x}+E_{10-x}+E_{-5-x} \\ &=(2.5+(-1.78)+0) \times 10^4 \\&=0.72\times 10^4\,\rm N/C \\\\ E_{P-y}&=E_{-10-y}+E_{10-y}+E_{-5-y}\\ &=(0+0.89+5) \times 10^4\\&=5.89\times 10^4\,\rm N/C \end{align*} These are the components of the net electric field at $P$. The net field $\vec{E}_P$ has the magnitude \begin{align*} E_P&=\sqrt{E_{P-x}^2+E_{P-y}^2} \\\\&=10^2 \sqrt{(0.72)^2+(5.89)^2}\\\\&=\boxed{593\quad \rm N/C} \end{align*}
Problem (12): A charge of $-38.6\,\rm \mu C$ and three other charges of $-27\,\rm \mu C$ are placed at the corners of a square, $0.25\,\rm m$ on a side. What is the strength and direction of the net electric field at the center of the square?
Solution: All charges are negative, and according to the definition, the electric field of a negative point charge is directed toward itself with a magnitude of $E=k\frac{|q|}{r^2}$ at distance $r$.
The desired point where the net electric field should be found is equidistant from each charge, midway between the square diameter, $d$. The Pythagorean theorem gives the square diameter as \begin{align*} d^2&=a^2+a^2\\&=2a^2 \end{align*} where $a$ is the square side. Thus, each charge is positioned at a distance of \begin{align*} r&=\frac d2=\frac{\sqrt{2}}{2}a \\\\ &=\frac{\sqrt{2}}{2} \times (0.25) \\\\ &=0.17\,\rm m\end{align*} Now, the magnitude of the electric field due to each charge at point $P$ is calculated as \begin{align*} E_{-38.6}&=k\frac{|q|}{r^2} \\\\ &=(9\times 10^9) \times \frac{(38.6\times 10^{-6})}{(0.17)^2} \\\\ &=12.02\times 10^6\,\rm N/C\end{align*} and for the charge $-27\,\rm \mu C$ is \begin{align*} E_{-27}&=k\frac{|q|}{r^2} \\\\ &=(9\times 10^9) \times \frac{(27\times 10^{-6})}{(0.17)^2} \\\\ &=8.40\times 10^6\,\rm N/C\end{align*} Stop for a moment and again see the free-body diagram carefully. The electric fields due to the two electric charges of $-27\,\rm \mu C$ at point $P$ have the same magnitude but are directed in opposite directions. As a result, these to $\vec{E}_{-27}$ cancel each other and do not contribute to the total electric field at point $P$.
Therefore, only the electric fields $\vec{E}_{-27}$ and $\vec{E}_{-38.6}$, located at the left upper and right bottom corners, contribute to the $\vec{E}_{net}$. The difference between these two fields (since these point in different directions) gives the net electric field at $P$ \begin{align*} E_{net}&=E_{-38.6}-E_{27} \\&=12.02-8.40 \\&= \rm N/C\end{align*}
On the page, electric field practice problems, you can find more questions.
Problem (13): An electron accelerates from rest to the south at a rate of $60\,\rm m/s^2$ in a uniform electric field. What is the magnitude and direction of the electric field?
Solution: The electron has a negative charge, so the force $\vec{F}=-e\vec{E}$ applied to it due to the electric field is in the direction opposite that of the field.
Because the field $\vec{E}$ is uniform and constant, the force is also constant, so we can use the constant acceleration kinematic equations.
According to Newton's second law $F=ma$. Substituting $F=eE$ into it, and solving for $E$ yields \begin{align*} E&=\frac{ma}{e}\\\\ &=\frac{(9.11\times 10^{-31})(60)}{(1.6\times 10^{-19})} \\\\&=\boxed{3.4\times 10^{-10}\,\rm N/C} \end{align*} Electron always travels in the opposite direction of the electric field. In this case, we are told that the electron is moving to the south, so the electric field must be directed to the north.
Problem (14): A $0.155-\rm kg$ ball is attached to a light thread and hangs vertically from the ceiling. This ball carries a net charge of $175\,\rm \mu C$. If the pendulum is placed in a horizontally directed uniform electric field of strength $1400\,\rm N/C$, find the angle the pendulum makes with the vertical line, assuming the system is in equilibrium.
Solution: Another interesting AP Physics C problem on electrostatics. Three forces are applied to such a pendulum floating in an external electric field. Downward weight force, $w=mg$, tension $T$ along the string, and the force due to the electric field, $F=qE$.
Once the pendulum is in an equilibrium position, all those forces are balanced together, meaning the net force exerted on the pendulum is zero. In such a situation, the components of the net force along the $x$ and $y$ axes must be set to zero.
The free-body diagram for this case is depicted in the following figure. The ball has a positive charge, so the force applied to it due to the electric field points to the right or positive $x$ axis.
In the next step, resolve the tension in the thread into its components as below \begin{gather*} T_x=T\sin\theta \\ T_y=T\cos\theta \end{gather*} Applying the equilibrium condition, setting the $F_{net-x}=0$ and $F_{net-y}=0$. \begin{gather*} F_{net-x}=0 \\ F_e-T_x=0 \\ qE-T\sin\theta=0 \\ \Rightarrow \quad T\sin\theta=qE \quad \rm (I) \end{gather*} And along the vertical axis, \begin{gather*} F_{net-y}=0 \\ T_y-w=0 \\ \Rightarrow\quad T\cos\theta=mg \quad \rm (II) \end{gather*} Dividing the first expression $\rm (I)$ by the second $\rm (II)$, an interesting formula is obtained that applies to almost all such questions. \[\boxed{\tan\theta=\frac{qE}{mg}}\] Substituting the numerical values into it, gives \begin{align*} \tan\theta&=\frac{qE}{mg} \\\\ &=\frac{(175\times 10^{-6})(1400)}{0.155\times 9.8} \\\\&=0.161 \end{align*} Taking the inverse tangent from both sides gives us the angle that the pendulum makes with the vertical when the system reaches equilibrium. \begin{gather*} \theta=\arctan(0.161) \\ \Rightarrow \quad \boxed{\theta=9^\circ}\end{gather*}
Problem (15): The total electric flux passing through a cubical box of side $30\,\rm cm$ is $1.42\times 10^3 \,\rm N\cdot m^2/C$. What charge is inside the box?
Solution: This is a problem on Gauss's law. According to this law, the total flux $\Phi_E=$ passing through a closed surface is equal to the net charge $Q_{enc}$ enclosed within the surface divided by $\epsilon_0$. \[\Phi_E=\frac{Q_{enc}}{\epsilon_0}\] Therefore, the net charge, meaning the sum of positive and negative charges inside the surface, is obtained as \begin{align*} Q_{enc}&=\epsilon_0 \Phi_E \\\\&=(8.85\times 10^{-12}) \times (1.42\times 10^3) \\\\&=12.56\times 10^{-9}\end{align*} Therefore, a charge or combination of charges with a magnitude of $12.56\,\rm nC$ enclosed within the box can produce such an electric flux.
Note that neither the location of the charge inside the box nor the shape of the surface surrounding the charge is important. If the closed surface is substituted by another surface, say a sphere, the amount of the charge obtained would not change.
Problem (16): A charge of $240\,\rm nC$ is placed at the center of the cube, $80\,\rm cm$ on a side, so that no other charges are nearby.
(a) What is the total flux through the whole of the cube?
(b) What is the flux through each face of the cube?
Solution: The charge is completely surrounded by the cube, so the net enclosed charge is $q_{enc}=2.4\times 10^3\,\rm nC$. Gauss's law relates the net charge inside a closed surface to the total electric flux $\Phi_E$ that passes through that surface.
(a) Applying Gauss's law and substituting the numerical values into it, we have \begin{align*} \Phi_E&=\frac{q_{enc}}{\epsilon_0} \\\\ &=\frac{240\times 10^{-9}}{8.85\times 10^{-12}}\\\\&=2.71\times 10^4 \quad \rm N\cdot m^2/C \end{align*} This number tells us how many electric field lines are passing through the closed surface.
Note that if the charge were not at the center, we would still get the same total flux because the charge is still completely surrounded by the surface.
(b) The charge is equidistant from all surfaces of the cube because it is placed at the center of the cube. As a result, each face of the cube receives an equal number of field lines or electric fluxes. \[\Phi_{tot}=6\phi_{face}\] On the other hand, the total flux is also determined using Gauss's law, $\Phi_{tot}=\frac{Q_{enc}}{\epsilon_0}$. Put everything together will end up as below \begin{align*} \phi_{face}&=\frac 16 \Phi_{tot} \\\\ &=\frac{Q_{enc}}{6\epsilon_0} \\\\ &=\frac{(240\times 10^{-9})}{6\times(8.85\times 10^{-12})} \\\\ &=\boxed{4.5\times 10^3\,\rm N\cdot m^2/C}\end{align*} This is the electric flux through each face of the cube.
In this part, the location of the charge inside the cube is important. If the charge were not centered, the faces near the charge would receive more field lines (or more flux), and faces further away would get fewer lines. Consequently, in this case, we could not use Gauss's law.
Author: Dr. Ali Nemati
Published: April 2, 2023
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
