Gauss's Law Problems and Solutions
Gauss's Law Definition:
In simple terms, Gauss's law states that the total number of electric field lines exiting a closed surface is directly proportional to the net electric charge $q_{in}$ enclosed within that volume.
Electric field lines are also defined as the electric flux $\Phi_E$ passing through any closed surface. Therefore, we can express Gauss's law mathematically using the following formula: \[\Phi_E=\oint{\vec{E}\cdot d\vec{A}}=\frac{q_{in}}{\epsilon_0}\] The closed-loop integral signifies integration over the entire closed surface.
Gauss's law is particularly useful for simplifying the calculation of the electric field associated with highly symmetrical charge distribution.
In the following, some questions with answers about Gauss's law are solved numerically and qualitatively which is helpful for class 12 students and college students.
Gauss's Law: Solved Practice Problems
Problem (1): Find the net electric charge inside the sphere below.
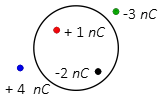
Solution: In the definition of Gauss’s law, the term “net charge” refers to the algebraic sum of all charges enclosed within the desired closed surface.
For the given sphere, the net charge inside can be calculated as follows: \[q_{in}={\rm (+1\,nC)+(-2\,nC)=-1\,nC}\] This means that the total charge enclosed within the sphere is negative and has a magnitude of 1 nC.
Problem (2): A point charge of $-2\,{\rm \mu C}$ is located at the center of a cube with sides $L=5\,{\rm cm}$. What is the net electric flux through the surface?
Solution: In this problem, computing the electric flux through the cube's surface using its direct definition as $\Phi_E =\vec{E}\cdot \vec{A}$ is a challenging and time-consuming task.
Gauss's law provides an alternative method for finding the electric flux. It states that the flux through a closed surface equals the enclosed charge divided by the vacuum permittivity $\epsilon_0$. Applying Gauss's law to the cube in this question, we calculate the flux as follows: \begin{align*}\Phi_E&=\frac{q_{in}}{\epsilon_0} \\ \\&=\frac{-2\times 10^{-6}}{8.85\times 10^{-12}}\\\\&=-226\times 10^{3}\quad {\rm \frac{N\cdot m^{2}}{C}}\end{align*} The minus sign indicates that the electric field lines are entering the cube.
Isn’t this content as valuable as a $10 private class? Please support me here. I worked hard to prepare this article.
Problem (3): A charge is located inside the cube (is not at the center)
(a) Find the net electric flux passing through the surface of the cube.
(b) Can you find the electric field on the surface of the cube using Gauss's law?

Solution: (a) Using Gauss's law the net electric flux is calculated as the net charge inside the cube divided by $\epsilon_0$. Therefore, substituting the numerical values, we have \begin{align*} \Phi_E&=\frac{q_{in}}{\epsilon_0}\\\\&=\frac{3\times 10^{-9}}{8.85\times 10^{-12}}\\\\&=339\quad {\rm \frac{N\cdot m^{2}}{C}}\end{align*}
(b) Gauss’s law is applicable and computable when there is high symmetry in the problem. In this example, the distances between the enclosed charge and each of the cube's surfaces are not equal. Due to this asymmetry, Gauss's law cannot be used to determine the electric field on the cube's surfaces.
Problem (4): A particle with charge Q is placed at the center of a cube with edges of L.
(a) What is the electric flux that passes through the entire cube?
(b) Find the electric flux through one of the faces of the cube.
(c) Calculate the electric field on one of the faces of the cube.
Solution:
(a) Using Gauss's law equation, $\Phi_E=q_{in}/\epsilon_0$, the electric flux passing through all surfaces of the cube is given by: \[\Phi_E=\frac{Q}{\epsilon_0}\]
(b) In this specific case, all the electric flux passes equally through the six faces of the cube. Thus, by dividing the total flux by six surfaces, we can find the flux through each of them. \[\phi_E=\frac{\Phi_E}{6}=\frac{Q}{6\epsilon_0}\] Note that if a charge is located everywhere except the center of a cube, we cannot use this approach. The flux through the surface close to the charge would be greater than the flux through the surface farther from the charge.
(c) We can not use Gauss's law to find the electric field on each surface of the cube, because all points of a surface are not at the same distance from the charge inside the cube. Consequently, the electric field cannot be factored out of the integral.
My income comes from your generous donations. Please support me.
Problem (5): A $3.5\,{\rm cm}$-radius hemisphere contains a total charge of $6.6\times 10^{-7}\, {\rm C}$. The electric flux through the rounded portion of the surface is $9.8\times {10}^4 \,{\rm \frac{N\cdot m^2}{C}}$. What is the flux through the flat base of the hemisphere?
Solution: The amount of electric flux $\Phi_E$ through any closed surface is related to the enclosed total charge by Gauss's law: \[\Phi_E=\frac{Q_{in}}{\epsilon_0}\] The hemisphere has two surfaces: the rounded portion and the flat base. Therefore, the total electric flux through it can be expressed as \[ \underbrace{\Phi_{E,r}+\Phi_{E,b}}_{\Phi_E}=\frac{Q_{in}}{\epsilon_0} \] Given that the flux through the rounded portion is $9.8\times {10}^4 \,{\rm \frac{N\cdot m^2}{C}}$, we can solve for the flux through the flat base: \[ 9.8\times {10}^4+\Phi_{E,b}=\frac{6.6\times {10}^{-7}}{8.854\times {10}^{-12}}\] Solving for $\Phi_{E,b}$: \[ \Phi_{E,b}=-2.34\quad {\rm \frac{N\cdot m^2}{C}} \]
To prepare for the AP Physics C exam, consider practicing similar questions on the electrostatic force.
Problem (medium): A cube with sides of $\ell=8.5\,\rm cm$ is positioned in a uniform electric field of strength $E=7500\,\rm N/C$ so that two of the faces are parallel to the field lines.
(a) What is the flux through each of the cube's six faces?
(b) What is net flux passing through the cube?
Solution: In this problem, a cube is placed into an external uniform electric field, and we are asked to find the flux through the entire cube and each of its faces. Let's consider this situation.
Assume a cube with six vectors (each of unit magnitude) perpendicular to its faces. These vectors are called unit normal vectors, $\hat{n}$. The flux through each face can be expressed as: \[\Phi_E=EA\cos\theta\] where $\theta$ is the vector between the electric field vector $\vec{E}$ and each of the unit vectors perpendicular to the faces, $\hat{n}$.
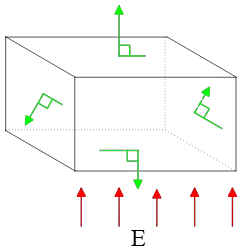
(a) Now insert such a cube into a uniform external electric field so that two of its faces—let’s call them “up” and “down”—are aligned with the direction of $\vec{E}$. Thus, the flux passing through these two faces can be calculated as follows: \begin{align*} \phi_{up}&=EA\cos 0^\circ \\&=7500\times (0.085)^2\times 1 \\&=54.2\quad \rm N\cdot m^2/C \\\\ \phi_{down}&=EA\cos 180^\circ \\&=7500\times (0.085)^2\times (-1) \\&=-54.2\quad \rm N\cdot m^2/C \end{align*} The electric fluxes through other faces of the cube is zero because their normal vectors make an angle of $90^\circ$ with the external electric field $\vec{E}$.
(b) The net electric flux is the sum of fluxes through all faces of the cube, assuming no charge is enclosed within the cube. Therefore, \begin{align*} \Phi_{net}&=\phi_{up}+\phi_{down}+\cdots \\ &=54.2+(-54.2)+0 \\ &=\boxed{0} \end{align*}
Problem (medium): A point charge $q$ is placed near a plane with approximately infinite extension. What is the flux through such a plane due to that point charge?
Solution: Since the plane is infinitely extended, the proximity of the electric charge to it does not significantly affect the situation. However, for better visualization, Let's assume the charge is extremely close to the plane. In this scenario, exactly half of the electric field lines — whether incoming or outgoing — penetrate the infinite plane.
On the other hand, the total electric flux (or the total number of field lines) produced by charge $q$, as determined by Gauss's law, is given by: \[\Phi=\frac{q}{\epsilon_0} \] Therefore, the total field lines that cross the infinite plane (i.e., the flux passing through that plane) can be computed as follows: \[\phi_{plane}=\frac 12 \Phi=\frac{q}{2\epsilon_0} \] For further exploration of electric charge properties, consider solving these problems on electric charge.
Problem (medium): A point charge of $0.0524\,\rm \mu C$ is positioned at the center of a tetrahedron.
(a) What is the total electric flux through its whole surface?
(b) What is the flux through one of its faces?
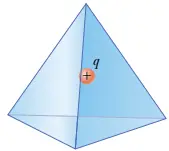
Solution: The electric flux $\Phi_E$ through any closed surface is related to the charge inside it by Gauss's law \[\Phi_E=\frac{Q_{in}}{\epsilon_0}\]
(a) According to the definition above, the total electric flux through the four sides of the tetrahedron is calculated as follows: \begin{align*}\Phi_E&=\frac{0.0524\times 10^{-6}}{8.85\times 10^{-12}} \\\\ &=5921\quad \rm N\cdot m^2/C \end{align*} Recall that the electric flux represents the number of field lines passing through a given surface. In this problem, approximately 5921 field lines pass through the entire surface of the tetrahedron.
(b) The above result represents the total flux passing through the four sides of the tetrahedron. A regular tetrahedron has four identical faces.
Since the charge is placed at the center of the tetrahedron, it is equidistant from each face. Consequently, the flux through each face is one-fourth of the total flux. \[\phi_E=\frac 14 \Phi_E = 1480\,\rm N\cdot m^2/C \] Therefore, the electric flux through one face of the tetrahedron is approximately $1480\,\rm N\cdot m^2/C$.
Practice Problem: In the figure below, a configuration of four closed surfaces and three charges of $-2Q$, $+Q$, and $-Q$ is shown. What is the electric flux through each surface?
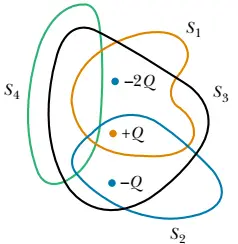
Solution: The electric flux $\Phi_E$ —representing the number of field lines passing through a given closed surface—is determined by Gauss’s law: \[\Phi_E=\frac{Q_{enclosed}}{\epsilon_0}\] As you can see, what matters is the presence of an electric charge and a closed surface surrounding it.
Now let’s analyze the situation for different colored closed surfaces:
There are two charges inside the orange closed surface, resulting in a total charge of $Q_{enclosed}=-2Q+Q=-Q$. Dividing this net charge by $\epsilon_0$, we get the electric flux through the orange surface \[\phi_{orange}=\frac{Q_{enc}}{\epsilon_0}=\frac{-Q}{\epsilon_0}\] Similarly, the flux through other colored closed surfaces are computed as below \begin{align*} \phi_{blue}&=\frac{Q_{enc}}{\epsilon_0}\\ &=\frac{-Q+Q}{\epsilon_0}=\boxed{0} \\\\ \phi_{black}&=\frac{Q_{enc}}{\epsilon_0} \\&=\frac{-2Q+Q-Q}{\epsilon_0} \\ &=\boxed{-\frac{2Q}{\epsilon_0}} \end{align*} No electric flux passes through the green closed surface because it does not surround any charge. \[\phi_{green}=\frac{Q_{inside}}{\epsilon_0}=\boxed{0}\]
Problem (medium): An electron is placed at a distance of $\ell/2$ just above the center of a square of edge $\ell$. Find the magnitude of the electric flux that passes through the square.
Solution: If we want to use Gauss's law to find the flux for such a configuration, we should construct a closed surface around the given charge. However, it’s essential to recall that Gauss’s law has limitations and is only applicable to situations with highly symmetric shapes or charge configurations.
Now consider the following scenario: If an electric charge (such as an electron or proton) is inserted at the center of a cube, the flux through each of its faces equals one-sixth of the total flux through that cube.
In our case, let’s imagine forming a cube with the given square so that the electron is positioned precisely at its center. By doing so, we can easily compute the flux passing through our original square.
The total electric flux through this imaginary cube is calculated as follows: \begin{align*} \Phi_{total}&=\frac{q_{inside}}{\epsilon_0} \\\\ &=\frac{-1.6\times 10^{-19}}{8.85\times 10^{-12}} \\\\ &=1.8\times 10^{-8}\,\rm N\cdot m^2/C \end{align*} As a result, the flux through the original square is \[\phi_E=\frac 16 \Phi_{total}=3\quad \rm nN\cdot m^2/C \] where $n=10^{-9}$.
Problem (6): A charge $q$ is located exactly at the center of the sphere. Find the electric field at the surface of the sphere.
Solution: We can use Gauss's law to find either the net electric flux through any closed surface or the electric field on the desired surface, provided that there is sufficient symmetry, as demonstrated in this example.
Using Gauss's law, the net electric flux through the surface of the sphere is given by: \[\Phi_E=\frac{q_{in}}{\epsilon_0}=\frac{q}{\epsilon_0}\] Next, use the definition of the flux to find the electric field at the sphere's surface: \begin{align*} \Phi_E &=\oint{\vec{E}\cdot d\vec{A}}\\ \\&=\oint{E dA \cos \theta} \\ \\ &=E \cos 0^\circ \oint{dA} \\ \\&=E(4\pi R^{2}) \end{align*} In the second line, we used the definition of scalar product, where $\theta$ is the angle between $\vec{E}$ and a unit vector normal (perpendicular) to the surface. In the last line, the integral over the whole surface of the sphere yields the area of a sphere.
Combining the first and second parts of the problem, we find the electric field on the surface of the sphere: \[4\pi R^{2}E=\frac{q}{\epsilon_0} \Rightarrow E=\frac{q}{4\pi\epsilon_0}\] Note: If the charge were located anywhere except the center of the sphere, we could not find the electric field on the sphere’s surface using Gauss’s law.
Problem (7): Charge $Q$ is distributed uniformly throughout an insulating sphere of radius $R$. Find the magnitude of the electric field at a point $R/2$ from the center.
Solution: If we have a symmetrical configuration, as in this case, use Gauss's law to find the electric field at each point of space. To do this, one must suppose a Gaussian surface at the desired point. In this problem, draw a Gaussian surface as a sphere of radius $R/2$ and proceed as follows \[\oint{\vec{E}.d\vec{A}}=\frac{Q_{in}}{{\epsilon }_0}\] Where $Q_{in}$ is the charge inside the Gaussian surface which here is the sphere of radius $R/2$ and is determined by the definition of volume charge density \begin{align*} \rho &=\frac{Q}{V} \\ \\ \Rightarrow Q_{in}&=\rho V_{Gauss} \\ \\ &=\rho \left(\frac{4}{3}\pi {\left(\frac{R}{2}\right)}^3\right) \\\\&=\frac{1}{6}\rho \pi R^3\end{align*} Substituting above into Gauss's law, we get \[E\oint{dA}=\frac{1}{6}\rho \pi R^3\] The electric field is taken out of the integral since it is constant at the location of the Gaussian sphere by symmetry considerations. The closed integral gives the area of the Gaussian surface.
Therefore \begin{align*} E\left(4\pi {\left(\frac{R}{2}\right)}^2\right)&=\frac{\frac{1}{6}\rho \pi R^3}{\epsilon_0} \\ \\ \Rightarrow E&=\frac{1}{4\pi {\epsilon }_0}\frac{2}{3}\rho \pi R\end{align*} Since the density of the sphere is uniform everywhere so substitute it by the total charge induced on the original sphere of radius $R$ as \[\rho =\frac{Q}{V}=\frac{Q}{\frac{4}{3}\pi R^3}\] Therefore
\begin{align*} E&=\frac{1}{4\pi {\epsilon }_0}\frac{2}{3}\frac{Q}{\frac{4}{3}\pi R^3}\pi R\\ \\ &=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{{2R}^2}\\ \\ &=\frac{Q}{8\pi {\epsilon }_0R^2}\end{align*}
Problem (8) A non-uniform, but spherically symmetric, distribution of charge has a charge density of $\rho\left(r\right)=\rho_0\left(1-\frac{r}{R}\right)$ for $(r<R)$ and $\rho\left(r\right)=0$ for $(r>R)$ where $\rho_0=\frac{3Q}{\pi R^3}$ is a positive constant.
(a) Show that the total charge contained in the charge distribution is $Q$
(b) Show that the electric field in the region ($r>R$) is identical to that produced by a point charge $Q$ at $r=0$.
(c) Obtain an expression for the electric field for $r<R$ and graph the magnitude of the $E(r)$ as a function of $r$.
(d) Find the value of $r$ at which the electric field $E(r)$ is a maximum, and find the value of that maximum field.
Solution:
(a) By definition, the total charge distributed in a region of space is $Q=\int{\rho\left(r\right)dV}$
\begin{align*} Q_{tot}&=\int{\rho\left(r\right)dV}\\ &=\int^R_0{\rho_0\left(1-\frac{r}{R}\right)\ 4\pi r^2dr}\\ &= 4\pi \rho_0{\left(\frac{1}{3}r^3-\frac{r^4}{4R}\right)}^R_0\\ &=\frac{1}{3}\pi \rho_0R^3\\ &=\frac{1}{3}\pi R^3\left(\frac{3Q}{\pi R^3}\right)=Q\\ \quad \Rightarrow Q_{tot}&=Q \end{align*}
(b) Use Gauss's law to find the electric field of a charge distribution inside and outside of the desired volume. The charge configuration has spherical symmetry so by symmetry consideration, the electric field must be radial. \begin{align*} \oint{\vec{E}\cdot \hat{n}dA}&=\frac{Q_{in}}{\epsilon_0} \\ \\ E_r\oint{dA}&=\frac{Q_{in}}{\epsilon_0} \\ \\ E_r\left(4\pi r^2\right)&=\frac{Q_{in}}{\epsilon_0} \\ \\ \Rightarrow E_r&=\frac{Q_{in}}{4\pi\epsilon_0r^2}\end{align*} if $r>R$ then the net charge inside the Gaussian surface $Q_{in}=\int{\rho\left(r\right)dV}=Q$ because the Gaussian surface encloses the overall sphere. Therefore \[E_r\left(r>R\right)=\frac{Q}{4\pi\epsilon_0r^2}\]
(c) From part (b) , $E_r=\frac{Q_{ins}}{4\pi\epsilon_0r^2}$ but the amount of enclosed charge in a Gaussian surface inside of the sphere is \begin{align*} Q_{in} &=\int{\rho\left(r\right)dV}\\ \\ &=\int^r_0{\rho_0\left(1-\frac{r}{R}\right)4\pi r^2dr}\\ \\ &=4\pi\epsilon_0{\left(\frac{1}{3}r^3-\frac{r^4}{4R}\right)}^r_0\\ \\ &=4\pi\epsilon_0\left(\frac{1}{3}r^3-\frac{r^4}{4R}\right) \end{align*} Therefore, the electric field in the region $r<R$ is obtained as below \[\Rightarrow E_r\left(r<R\right)=\frac{\rho_0}{\epsilon_0}\left(\frac{1}{3}r-\frac{r^2}{4R}\right)\]
(d) we must find the maximum value of the electric field inside the sphere so
\begin{align*}\frac{d}{dr}E_r\left(r<R\right)&=0 \\ \\ \frac{\rho_0}{\epsilon_0}\left(\frac{1}{3}-\frac{r}{2R}\right)&=0 \\ \\ \Rightarrow r&=\frac{2}{3}R\end{align*} Substituting this value of $r$ into the above electric field inside the sphere, we have
\[E_r\left(r=\frac{2}{3}R\right)=\frac{\rho_0}{\epsilon_0}\left(\frac{2}{9}R-\frac{R}{9}\right)=\frac{\rho_0}{9\epsilon_0}R\]
Problem (9): A solid conducting sphere carrying charge $q$ has radius $a$. It is inside a concentric hollow conducting sphere with an inner radius $b$ and outer radius $c$. The hollow sphere has no net charge.
Derive expressions for the electric field magnitude in terms of the distance $r$ from the center for the region $r<a\ ,\ a<r<b\ ,\ b<r<c\ $, and $r>c$.
(a) Graph the magnitude of the electric field as a function of $r$ from $r=0$ to $r=2c$.
(b) What are the charges on the inner surface and the outer surface of the hollow sphere?
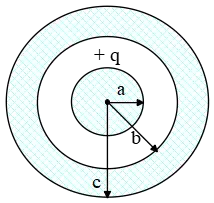
Solution:
In such problems, Gauss’s law allows us to find the electric field everywhere.
(a) Gauss's law states that the electric flux through any closed surface $S$ is equal to the charge enclosed by it divided by $\epsilon_0$: \[\oint_s{\vec{E}.\hat{n}dA}=\frac{Q_{enc}}{\epsilon_0}\]
To apply Gauss's law, we must first consider a closed surface called a Gaussian surface. This surface has the same symmetry as the electric field. In this case, the Gaussian surface must be a spherical surface of radius $r$ concentric with the conducting charged sphere of radius $a$.
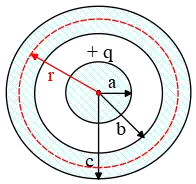
Note: Although Gauss's law is valid for any surface surrounding a charged configuration, it is most useful when we choose a Gaussian surface that matches the original symmetry of the problem.
To find the electric field in the region $r<a$, the Gaussian surface is inside the sphere of radius $a$. Since inside this surface, there is not any charge, so there is no flux through it, thus \[\oint_s{\vec{E}\cdot \hat{n}dA}=\frac{Q_{in}}{\epsilon_0}=0\Rightarrow E\left(r<a\right)=0\] In the region $a<r<b$, the Gaussian surface encloses the charged sphere $q$, so \begin{align*}\oint_s{\vec{E}\cdot \hat{n}dA}&=\frac{Q_{in}}{\epsilon_0}\\ \\ E\oint_s{dA}&=\frac{q}{\epsilon_0} \\ \\ \Rightarrow E\left(a<r<b\right)&=\frac{q}{4\pi \epsilon_0r^2}\end{align*} Since $E$ is constant and perpendicular everywhere on the Gaussian surface, so we take it out of the integral.
The closed integral $\oint_s{dA}$ is the surface area of the sphere. In the case of a sphere, the normal vector $\hat{n}$ is along the radial direction i.e. $\hat{n}=\hat{r}$.
Because inside the Gaussian surface, there is a positive charge, the electric field points away from the center or is radially outward, i.e., $\vec{E}=E\left(r\right)\hat{r}$.
Region $b<r<c$ lies inside the conductor. Using the fact that the electric field inside a conductor is zero, we get $E\left(b<r<c\right)=0$.
In region $r>c$, the net charge encloses by the Gaussian surface is $+q$, so in this region the electric field is \begin{align*}\oint_s{\vec{E}\cdot \hat{n}dA}=\frac{Q_{in}}{\epsilon_0}=\frac{q}{\epsilon_0}\\ \\ \Rightarrow E\left(r>c\right)&=\frac{q}{4\pi \epsilon_0r^2}\end{align*} The graph is as follows
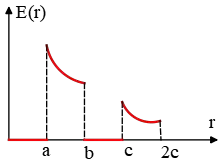
(b) The free charge $q$ inside the sphere of radius $a$ induces charge $-q$ on the inner surface and subsequently induces charge $+q$ on the outer surface of the spherical shell.
Page Published: 2/28/2021
Last Update: Sep 16, 2022
Author: Dr. Ali Nemati
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
