Inclined Planes: Practice Problems with Solutions

In this article, we explore the topic of inclined planes in physics with several solved practice problems designed for high school and college students.

Get ready to sharpen your problem-solving skills and deepen your knowledge of this fundamental concept in physics!

Save time, boost your score! Get our comprehensive 31-page equation sheet and ace the AP Physics 1 Exam in $2025$. Limited time offer for just $\$ 10$! (Download free PDF sample).

Inclined Plane Problems without Friction:

Problem (1): A 45 kg object rests on a 30° inclined plane.
(a) What force is exerted down the inclined plane?
(b) What force acts perpendicular to the plane?

Solution: In all inclined plane problems, the first step is to choose a suitable coordinate system. It is common to choose the positive direction along and down the plane, with the up direction perpendicular to the plane.

The weight force and normal force always act on an object resting on a smooth inclined plane (without friction). The normal force acts along the upward direction of our chosen coordinate system, while the weight force should be decomposed into components in the tilted coordinate system.

As shown in the figure below, one component of the weight force is parallel to the plane and acts downward, while the other is perpendicular and acts in the $-y$ direction.

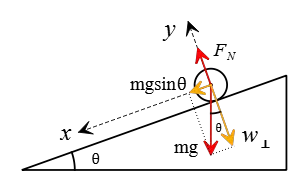
Inclined plane problem - free body diagram

(a) With these brief explanations, the downward weight component parallel to the slope always pulls an object down on an inclined plane.

Using trigonometry, we can find that this component is $mg\sin\theta$, where $m$ is the mass of the object and $\theta$ is the angle of the inclined plane. \begin{align*} F_x&=mg\sin\theta \\ &=45\times 9.8\sin 30^\circ \\ &=\boxed{220.5\,\rm N} \end{align*}
(b) As you noticed along the perpendicular direction to the plane, two forces act on the object while it has no motion (i.e., $a_y=0$). To determine the force acting perpendicular to the plane, we need to find the normal force. Applying Newton's second law to this direction gives us the normal force on the object \begin{gather*} F_{net-y}=ma_y \\\\ F_N-w_{\bot}=0 \\\\ F_N-mg\cos\theta=0 \\\\ \Rightarrow F_N=\underbrace{mg\cos\theta}_{w_{\bot}} \end{gather*} Substituting the given numerical values into this, we have \[\boxed{F_N=45\times 9.8 \cos 30^\circ=382\,\rm N}\]

Problem (2): A car of mass $m$ is at the top of an icy 15° slope whose length is 30 m.
(a) Find the acceleration of the car.
(b) How long does it take for the car to reach the bottom?
(c) How fast is the car at the bottom?

Solution: The slope is icy, so it has no friction. Recall from the previous problem that the downward weight component parallel to the inclines is $mg\sin\theta$. This force causes the car to go down from the top of the inclined plane.

(a) Because the incline is frictionless, the only force that acts on the car is $w_{\parallel}=mg\sin\theta$. Applying Newton's second law and substituting the numerical value yields \begin{gather*} F_{net}=ma_x \\\\ mg\sin\theta=ma_x \\\\ \rightarrow a_x=g\sin\theta \\\\ a_x=(9.8) \sin 15^\circ \\\\ \Rightarrow \boxed{a_x=2.6\,\rm m/s^2} \end{gather*} As this equation shows, the acceleration along the inclined plane does not depend on the object's mass.

(b) The car starts its motion from rest, i.e., $v_0=0$. The car's acceleration is also found in the previous part. The only kinematic equation that relates these known values together is $\Delta x=\frac 12 at^2+v_0t$, where $\Delta x$ is the total displacement traveled by the object along the slope, which here is $\Delta x=30\,\rm m$. \begin{gather*} \Delta x=\frac 12 at^2+v_0t \\\\ 30=\frac 12 (2.6)t^2+0 \\\\ \rightarrow t=\sqrt{\frac{2\times 30}{2.6}} \\\\ \Rightarrow \boxed{t=4.8\,\rm s} \end{gather*}
(c) To find the velocity at the bottom, we can use either of two kinematic equations $v^2-v_0^2=2a\Delta x$ or $v=v_0+at$. We choose the first equation and put the numbers into it \begin{gather*} v^2-v_0^2=2a\Delta x \\\\ v^2-0=2(2.6)(30) \\\\ \Rightarrow \boxed{v=12.48\,\rm m/s} \end{gather*}

If you found this article helpful, I would greatly appreciate your support. It allows me to continue producing valuable content for readers like you.

Problem (3): A hockey puck with an acceleration of $6\,\rm m/s^2$ is sliding down a $12-\rm m$-long frictionless ramp.
(a) What is the angle of the ramp?
(b) How long does it take the puck to reach the bottom?
(c) If the mass of the puck is doubled, how does its acceleration change down the incline?

Solution: The ramp or inclined plane has an unknown angle $\theta$ that we need to determine. We assume the positive $x$-axis to be down the ramp.

(a) The only force that pulls the puck down the slope and accelerates it is the component of weight force parallel to the inclined plane, $w_{\parallel}=mg\sin\theta$. Therefore, by using the second law, we get \begin{gather*} F_{net}=ma_x \\\\ mg\sin\theta=ma_x \\\\ \Rightarrow a_x=g\sin\theta \end{gather*} Substituting the numerical values into this, solving for angle $\theta$, and taking the inverse sine of both sides, we get \begin{align*} \theta &=\sin^{-1} \left(\frac{a_x}{g}\right) \\\\ &=\sin^{-1} \left(\frac{6}{9.8}\right) \\\\ &=37.7^\circ \end{align*}
(b) The puck is initially held at rest, $v_0$, and the ramp's length $\Delta x=12\,\rm m$ is also known, so use the following kinematic equation to find the required time. \begin{gather*} \Delta x=\frac 12 at^2+v_0t \\\\ 12=\frac 12 (6)t^2+0 \\\\ \Rightarrow \boxed{t=2\,\rm s} \end{gather*}
(c) In part (a), we saw that the acceleration of an object sliding down a frictionless ramp depends on $g$ and the ramp's angle $\theta$, but not on the mass $m$. Therefore, by doubling the puck's mass, its acceleration does not change along the inclined plane. \[a_{new}=a_{old}=6\,\rm m/s^2\]

Problem (4): A $1500-\rm kg$ car is at rest on a frictionless hill inclined at $17^\circ$.
(a) Sketch a free-body diagram and calculate the components $w_{\parallel}$, $w_{\bot}$, and the normal force acting on the car.
(b) Find the car's acceleration when it is released.
(c) If the hill is $55-\rm m$-long, what would be the car's final velocity at the bottom of the hill?
(d) How long will it take for the car to reach the end of the hill?

Solution: (a) Two forces act on the car—the normal force perpendicular to the hill, $F_N$, and the weight force, $w=mg$. The weight force has two components that are parallel $w_{\parallel}$ and perpendicular $w_{\bot}$ to the inclined plane.

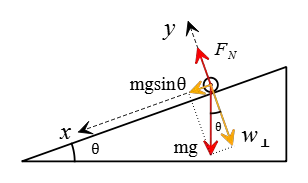
Inclined plane problem - weight components and normal force

From the above free-body diagram, we can calculate these components as \begin{align*} w_{\parallel} &=mg\sin\theta \\ &=(1500\times 9.8) \sin 17^\circ \\ &=\boxed{4297.86\,\rm N} \\\\ w_{\bot}&=mg\cos\theta \\&=1500\times 9.8\cos 17^\circ \\&=\boxed{14057.68\,\rm N} \end{align*}
(b) The car perpendicular to the hill does not have acceleration, so $a_y=0$. However, the car parallel to the hill is accelerating $a_x=?$, and we need to determine $a_x$.

By applying Newton's second law along the $x$- and $y$-axes on the hill, we get \begin{gather*} F_{net-x}=ma_x \\ mg\sin\theta=ma_x \\ \Rightarrow a_x=g\sin\theta \\\\ F_{net-y}=ma_y \\ F_N-w_{\bot}=0 \\\Rightarrow F_N=w_{\bot}=\boxed{14057.68\,\rm N} \end{gather*} Therefore, the car's acceleration is \[a_x=9.8\times \sin 17^\circ =2.86\,\rm m/s^2 \]
(c) This part is related to a kinematics problem in physics. The car starts from rest ($v_0=0$) and is displaced along the hill by $\Delta x=55\,\rm m$. Its acceleration is also found in the previous part, $a_x=2.86\,\rm m/s^2$. Using the following kinematics equation and solving for $v$, we get \begin{gather*} v^2-v_0^2=2a\Delta x \\\\ v^2-0=2(2.86)(55) \\\\ \Rightarrow \boxed{v=17.73\,\rm m/s} \end{gather*}
(d) To find the unknown time $t$, we apply the equation $v=v_0+at$ and solve as follows: \begin{gather*} v=v_0+at \\ 17.73=0+(2.86)t \\ \Rightarrow \boxed{6.2\,\rm s} \end{gather*}

If you enjoyed this article, please consider making a small donation to help fund my future work.

Problem (5): A box with a mass of $45\,\rm kg$ is held at rest by a rope on a frictionless ramp inclined at $30^\circ$. Draw a free-body diagram and find the value of the tension force exerted by the rope.

Solution: The box is at rest, so there is no motion or acceleration along the $x$- and $y$- axes parallel and perpendicular to the inclined plane, respectively.

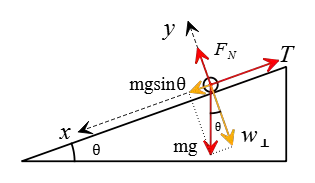
Inclined plane problem with tension force

As the free-body diagram shows, the tension force is upward on the ramp, and the weight component $mg\sin\theta$, as always, is down the incline. Applying Newton's second law gives us \begin{gather*} F_{net-x}=ma_x \\\\ T-mg\sin\theta=0 \\\\ \Rightarrow T=mg\sin\theta \end{gather*} By substituting the given values into this, the value of tension force is obtained as follows \[T=45\times 9.8\times \sin 30^\circ=\boxed{220.5\,\rm N}\]

Inclined Plane Problems with Friction:

Problem (6): A slippery object slides down a ramp of $9\,\rm m$ long inclined at $10^\circ$. The kinetic friction between the object and the ramp is $\mu_k=0.06$. How long does it take for the object to reach the bottom?

Solution: The only force exerted on the object and forcing it to go down is the component of weight parallel to the inclined plane. The kinetic friction force up the incline opposes the weight force down the incline. Balancing these two exerting forces gives acceleration to the slippery object.

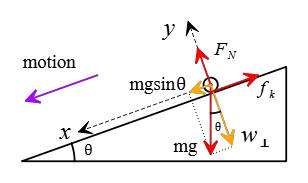
Inclined plane problem along with friction force

Consider the downward direction of the ramp as the positive $x$ direction. Applying Newton's second law to forces along the inclined plane yields \begin{gather*} F_{net-x}=ma_x\\\\ mg\sin\theta-f_k=ma_x \\\\ mg\sin\theta -\mu_k N=mg \end{gather*} where in the last line, we used the definition of friction force. Applying the above law along the direction normal to the slope, given that in this direction the object does not move, we can find the normal force on the object \begin{gather*} F_N-mg\cos\theta=0 \\ \Rightarrow F_N=mg\cos\theta \end{gather*} Substituting this into the first expression and removing the common factor $m$, we get the object's acceleration along the rough inclined plane \begin{align*} a_x &=g(\sin\theta-\mu_k \cos\theta) \\\\ &=(9.8) \left(\sin 10^\circ-(00.6) \cos 10^\circ \right) \\\\ &=1.12\,\rm m/s^2 \end{align*} Assume the object was initially at rest, $v_0=0$. On the other hand, the total displacement or distance that the object covers is the length of the incline, $\Delta x=9\,\rm m$.

By knowing that information, we can use the displacement kinematic equation $\Delta x=\frac 12 at^2+v_0t$ to find the required time as below \begin{gather*} \Delta x=\frac 12 at^2+v_0t \\\\ 9=\frac 12 (1.12)t^2 + 0 \\\\ \rightarrow t=\sqrt{\frac{2\times 9}{1.12}} \\\\ \Rightarrow \quad \boxed{t=4\,\rm s} \end{gather*} Thus, our slippery object takes about $4$ seconds to reach the bottom of the inclined plane.

Problem (7): A $54.6\,\rm kg$ block is resting on a $7^\circ$ slope.
(a) What is the normal force acting on the block?
(b) What is the friction force holding the block on the slope?

Solution: except for the weight and friction forces, no other external forces at angles, act on the block resting on the inclined plane.

(a) Recall that, as always in all inclined plane problems, in the presence of these two forces, the normal force on an object on a slope is $F_N=mg\cos\theta$. Substituting the given values gives us \[F_N=54.6\times 9.8\times \cos 7^\circ=531\,\rm N\]
(b) The block is at rest on the slope, so there should be a force to oppose the weight component $mg\sin\theta$ to hold the block motionless on the inclined plane. This opposing force is the same friction force.

Consequently, in this special case, the friction force is found to be $f=mg\sin\theta$ whose magnitude is also as below \[f=54.6\times 9.8\times \sin 7^\circ= 65.2\,\rm N\]

Problem (8): A $46.5\,\rm kg$ crate is resting motionless on a ramp inclined at an angle of $20^\circ$. What is the coefficient of friction between the crate and the ramp?

Solution: The crate does not have acceleration along the ramp, so the downward weight component $mg\sin\theta$ must be balanced with the upward friction force on the incline. Therefore, we have $f=mg\sin\theta$. On the other hand, in these situations, the normal force acting on the object also has a magnitude of $F_N=mg\cos\theta$.

From the problems on the coefficient of static friction force, we remember that $f=\mu F_N$. Combining everything together, we get \begin{gather*} f=\mu F_N \\\\ mg\sin\theta=\mu (mg\cos \theta) \\\\ \rightarrow \mu=\frac{\sin\theta}{\cos\theta}=\tan\theta \end{gather*} Substituting the numerical values into this equation, we get \[\boxed{\mu=\tan 20^\circ=0.36} \]

This question has an important note for us. It tells us that when an object is either at rest (motionless) or moving with a constant velocity along a rough inclined plane, the coefficient of friction between the incline and the object is independent of the object's mass and only depends on the angle of the incline.

Problem (9): A box weighing $95\,\rm N$ is held at rest on a slope inclined at an angle of $25^\circ$.
(a) Find the magnitudes of the weight forces parallel and perpendicular to the inclined plane.
(b) Assuming the coefficient of static friction between the box and the incline is $0.55$, what is the maximum frictional force?
(c) Does the box move? If yes, at what rate does the box move down? If not, with what $\mu_s$ will the box be on the verge of sliding?

Solution: The weight of the box and the angle of incline $\theta=25^\circ$ are given.
(a) As you have learned so far, the weight force components parallel ($w_\parallel$) and perpendicular ($w_\bot$) to the incline are given by the following formulas: \begin{align*} w_\parallel&=mg\sin\theta \\&=95\times \sin 25^\circ \\ &=\boxed{40.14\,\rm N} \\\\ w_\bot&=mg\cos\theta \\&=95\cos 25^\circ \\&=\boxed{86\,\rm N} \end{align*}
(b) Static friction is the maximum frictional force that opposes motion and prevents an object from moving. It is also defined as $f_{s,max}=\mu_s F_N$, where $F_N$ is the normal force exerted on an object sitting on the incline.

Recall that in the case of an external force applied to the object at an angle, the magnitude of the normal force is calculated as follows: \begin{align*} f_{s,max}&=\mu_s (mg\cos\theta) \\ &=(0.55)(95) \cos 25^\circ \\ &=\boxed{47.35\,\rm N} \end{align*}
(c) To determine whether the box moves down the incline or remains at rest, we must compare the weight component $w_\parallel$ down the incline with the maximum static friction upward along the incline.

In the last two parts, we found that \[\underbrace{w_\parallel}_{40.14} < \underbrace{f_{s,max}}_{47.35} \] The force opposing the motion is greater than the force pulling the box down the inclined plane, so the box remains motionless.

For the box to start sliding down from the top of the incline, the parallel weight component $w_\parallel$ must be equal to the frictional force. Equating these two forces and solving for $\mu_s$, we obtain the required coefficient of static friction to put the box on the verge of sliding. \begin{gather*} w_\parallel =f_{s,max} \\ mg\sin\theta =\mu_s (mg\cos\theta) \\\\ \rightarrow \mu_s=\tan\theta \\ \Rightarrow \boxed{\mu_s=\tan 25^\circ=0.466}\end{gather*}

Problem (10): A box of mass $35\,\rm kg$ sits on a $30^\circ$ incline. Consider these two cases and find out what is being said.
(a) If the box does not move down the incline, what can you say about the static frictional force acting on the box?

(b) If the box slides down the incline with an acceleration of $3\,\rm m/s^2$, find the kinetic frictional force and the coefficient of kinetic friction between the box and the incline.

Solution: Like any other inclined plane practice problem, first find the parallel and perpendicular components of the object's weight along the incline as below \begin{align*} w_\parallel&=mg\sin\theta \\&=35\times 9.8 \times \sin 30^\circ \\ &=\boxed{171.5\,\rm N} \\\\ w_\bot&=mg\cos\theta \\&=35 \times 9.8 \cos 30^\circ \\&=\boxed{297.0\,\rm N} \end{align*} Now we want to examine the behavior of the box along the slope with/without the frictional force.

(a) If the box is not going to slide down the incline, the net force along the slope must be zero. This means that the parallel component of the weight, $w_\parallel$, must be balanced by the static frictional force, $f_s$. Therefore we have: \[f_s = w_\parallel \Rightarrow \boxed{f_s = 171.5\,\rm N}\] This is the actual static friction force required to keep the box at rest on the incline.

(b) If the box slides down the incline with an acceleration of $3\,\rm m/s^2$, it means that the net force along the slope is positive and equal to the product of the mass and the acceleration, $ma_x$. This implies that the parallel component of the weight, $w_\parallel$, is greater than the kinetic frictional force, $f_k$. Therefore, we can write: \[w_\parallel-f_k=ma_x\] To find the value of $f_k$, we need to rearrange the equation and plug in the given values: \begin{align*} f_k &= w_\parallel - ma_x \\ &= 35\times 9.8 \times \sin 30^\circ - (35)(3) \\ &= 66.5\,\rm N \end{align*} Therefore, the kinetic frictional force is: \[f_k = 66.5\,\rm N\] To find the coefficient of kinetic friction, $\mu_k$, we need to use the formula for $f_k$, which is given by: \[f_k = \mu_k F_N\] where $F_N$ is the normal force, which is equal and opposite to the perpendicular component of the weight, $w_\bot$. The formula for $w_\bot$ is given by: \[w_\bot = mg\cos\theta\] Plugging in the given values, we get: \begin{align*} w_\bot &= 35\times 9.8 \times \cos 30^\circ \\ &= 297.0\,\rm N \end{align*} Therefore, the normal force is: \[F_N = 297.0\,\rm N\] To find the value of $\mu_k$, we need to divide both sides of the equation by $F_N$: \[\mu_k = \frac{f_k}{F_N} = \frac{66.5}{297.0} = 0.22\] Therefore, the coefficient of kinetic friction is: \[\mu_k = 0.22\]

Problem (11): A $5-\rm kg$ box is placed on a surface with a kinetic coefficient of friction of $0.28$. The surface is slowly raised and reaches an angle of $48^\circ$. What would be the acceleration of the box down the incline?

Solution: In the earlier questions, we saw that the acceleration of an object on a rough inclined plane is written as \[a=g(\sin\theta-\mu_k \cos\theta)\] Substituting the numerical values into it gives \begin{align*} a&=(9.8) \left(\sin 48^\circ-(0.28)\cos 48^\circ \right) \\&=\boxed{5.44\,\rm m/s^2} \end{align*}

Problem (12): A car weighing $2\times 10^4\,\rm N$ is at rest at the bottom of a $22^\circ$ hill. Several people are pushing the car uphill with a combined force of $8500\,\rm N$ parallel to the incline. (Assume the hill has negligible friction.)
(a) What acceleration does the car obtain?
(b) The people push on the car for $15\,\rm s$. How far does the car go up the incline?

Solution: Two forces are acting on the car in this direction: the parallel component of the weight,$w_{\parallel}$, and the pushing force, $F_p$. The net force is given by \[F_{net} = F_p - w_\parallel\] As always the weight components are found as follows: \begin{align*} w_{\parallel}&=mg\sin\theta \\&= (2\times 10^4) \sin 22^\circ \\ &=\boxed{7492.13\,\rm N} \\\\ w_{\bot}&=mg\cos\theta \\ &=(2\times 10^4) \cos 22^\circ \\&=\boxed{18543.67\,\rm N} \end{align*} Take the direction of the movement as the positive $x$-direction. In this case, the weight component $w_{\parallel}$ is in the negative $x$ direction or downhill, but the pushing force, exerted by people, is uphill.

(a) Applying the second law along the $x$-direction (on the inclined plane) gives us \begin{gather*} F_{net-x}=ma_x \\ F_{ext}-w_{\parallel}=ma_x \\ 8500-7492.13=2040.81 a_x \\ \Rightarrow \boxed{a_x=0.49\,\rm m/s^2} \end{gather*}
(b) The car is initially at rest at the bottom of the hill, $v_0=0$. The only kinematic relationship that connects our known values, $a=0.49\,\rm m/s^2$ and $t=15\,\rm m$, is $\Delta x=\frac 12 at^2+v_0t$, where $\Delta x$ is the distance traveled on the incline. Plugging in the values, we get: \begin{align*} \Delta x&=\frac 12 at^2+v_0t \\\\ &=\frac 12 (0.49)(15)^2+0 \\\\ &=\boxed{55.125\,\rm m} \end{align*}

Problem (13): A box weighing $175\,\rm N$ rests on a horizontal surface with a static coefficient of friction of $\mu_s=0.85$.
(a) At what angle should the surface be raised so that the box would just start to move?
(b) Assume the kinetic coefficient of friction is $\mu_k=0.42$. At what angle should the ramp be lowered so that the box moves without acceleration?

Solution: On the horizontal surface, the only forces initially acting on the box are the normal $F_N$ and the weight $w=mg$ forces. As soon as it makes an angle with the level, no longer the weight pulls the box perpendicularly.

At this point, we must choose a coordinate system on the inclined plane, as you saw in the previous problems.

(a) Before reaching a certain angle, the box remains at rest because the upward static friction force on the incline is greater than the downward force of $mg\sin\theta$ along the incline. As the angle increases, the weight component parallel to the incline gradually increases until it equals the maximum static friction force, causing the box to be on the verge of slipping downward. This can be expressed as $f_{s,max}=mg\sin\theta$, which can be rearranged to solve for the static coefficient of friction $\mu_s$. \begin{gather*} f_{s,max}=mg\sin\theta \\ \mu_s F_N=mg\sin\theta \\ \mu_s (mg\cos\theta)=mg\sin\theta \\ \Rightarrow \boxed{\mu_s=\tan \theta} \end{gather*} The desired angle is then found by taking the arctangent (inverse of tangent) of $\mu_s$. Using this method, we find that the box will remain at rest until the surface reaches an angle of approximately $40.36^\circ$. \begin{align*} \theta&=\arctan{\mu_s} \\ &=\arctan{0.85} \\ &=\boxed{40.36^\circ} \end{align*}
(b) As you have seen in part (a), the box is at rest until the surface reaches an angle of about $40^\circ$. Beyond that angle, the box would accelerate downslope. Now, by reducing the angle we can make a situation in which the box would travel with constant velocity (no acceleration). This occurs when the weight force component $mg\sin\theta$ down slope becomes equal to the kinetic friction force $f_k=\mu_k F_N$ upslope. Equating these two forces will give us the desired angle \begin{gather*} f_k=mg\sin\theta \\ \mu_k (mg\cos\theta)=mg\sin\theta \\ \Rightarrow \boxed{\tan\theta=\mu_k} \end{gather*} Substituting the given value into this equation and taking the inverse tangent of both sides, we get \begin{gather*} \tan\theta=0.42 \\ \rightarrow \theta =\tan^{-1}(0.42)=\boxed{22.7^\circ} \end{gather*}

Summary:

In this long article, we solved some problems on inclined planes with and without frictional force. In both cases, we learned that the normal force acting perpendicularly on an object on an inclined plane is written as $F_N=mg\cos\theta$.

On the other hand, the weight force component $w_{\parallel}$ parallel to the incline pulls the object downslope whose magnitude is $w_{\parallel}=mg\sin\theta$.

Author: Dr. Ali Nemati
Page Published: Sep 18, 2022