Coefficient of Friction Problems and Solutions
This tutorial covers some problems on friction force and coefficients of friction, which are important concepts in physics. You will see how to apply the formulas and principles of friction to various situations, such as sliding, rolling, and inclined planes.
The solutions are explained step by step, with diagrams and equations.
This tutorial is suitable for high school and college students who want to practice and improve their skills on friction problems.
Coefficient of kinetic friction: Problems
Problem (1): A constant force of $10\,{\rm N}$ is applied to a $2-{\rm kg}$ crate on a rough surface that is sitting on it. The crate undergoes a frictional force against the force that moves it over the surface.
(a) Assuming the coefficient of friction is $\mu_k=0.24$, find the magnitude of the friction force that opposes the motion.
(b) What is the net force on the crate?
(c) What acceleration does the crate obtain?
Solution: The kinetic friction force is the force that opposes the motion of a moving object. Its magnitude is given by the formula $f_k=\mu_k F_N$, where $\mu_k$ is the coefficient of kinetic friction, and $F_N$ is the normal force on the object due to contact with a surface.
In all problems involving the coefficient of friction, you must apply Newton's second law in the vertical direction to find the normal force if it is not given.
(a) The crate does not move vertically or lift off the surface, so the forces in this direction are balanced. The free-body diagram below shows that two forces act on the crate: an upward normal force $F_N$, and a downward weight force $W=mg$.
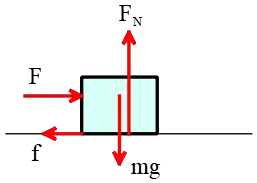
Thus, \[F_N=mg=2\times 10=20\,{\rm N}\] Now that the normal force is known, we can use the kinetic friction force formula $f_k=\mu_k F_N$ to find its magnitude: \[f_k=\mu_k F_N=0.24\times 20=4.8\,{\rm N}\]
(b) '' Net force'' means the sum vector of forces. In the horizontal direction, two forces act on the crate: external force $F$, and friction force $f$. These two forces apply in the opposite direction.
The subtraction of these two forces gives us the net (resultant) force on the crate. So, \[F_{net}=F-f_k=10-4.8=5.2\,{\rm N}\]
(c) According to Newton's second law of motion, if a force of $F$ is applied to a body of mass $m$, then it undergoes an acceleration whose magnitude is given by $a=\frac{F}{m}$. So, the acceleration that this crate experiences is found as \[a=\frac{F_{net}}{m}=\frac{4.8}{2}=2.4\,{\rm m/s^2}\]
Our journey is taking us to the US, and we’re counting on your generosity (here) to help us maintain and enhance our website during this transition.
Problem (2): A $75-{\rm kg}$ box is pulled over a rough surface using a horizontal force of $100\,{\rm N}$ at a constant velocity. Find the coefficient of friction between the box and the surface.
Solution: All coefficient of friction problems and Newton's second law of motion are closely related topics. The box moves at constant velocity.
According to the definition of average acceleration, $a=\frac{\Delta v}{\Delta t}$, constant speed or velocity means the acceleration is zero (This is valid for straight-line motion).
On the other hand, zero acceleration means no net force on the object, $F_{net}=ma=0$.
To meet this condition, the forces must balance each other. Consequently, the pulling force $F$ must equal the opposing friction force $f_k$, so \[F=f_k=\mu_k F_N \Rightarrow \mu_k=\frac{F}{F_N}\] Set the net force in the vertical direction to zero, since the box does not lift off the surface. Thus, the normal force $F_N$ is \[F_N=mg=75\times 10=750\,{\rm N}\] Therefore, the coefficient of friction is determined as \[\mu_k=\frac{F}{F_N}=\frac{100}{750}=0.13\]
Problem (3): Assume the coefficient of kinetic friction between a $22-{\rm kg}$ box and a rough floor is $0.25$.
(a) What horizontal force is needed for the box to move at a constant speed?
(b) Now, assuming $\mu_k=0$, what horizontal external force is required?
Solution: As before, the motion is along a horizontal straight path, so the constant speed means there is no acceleration $a=0$. Thus, the net force in this direction is zero, $F_{net}=ma=0$.
If the external force equals the magnitude of friction force, then the net force on the object is zero, and it moves at a constant speed.
(a) With the given explanation above, we must have \[F=f_k \Rightarrow \text{constant speed}\] The kinetic friction force, $f_k=\mu_k F_N$, depends on the magnitude of the normal force, which in this case is \[F_N=mg=22\times 10=220\,{\rm N}\] So, the magnitude of friction is \[f_k=\mu_k F_N=0.25\times 220=55\,{\rm N}\] Consequently, a constant force of $F=55\,{\rm N}$ parallel to a surface having $\mu_k=0.25$, forces a 22-kg object to move at a constant speed.
(b) When the coefficient of friction is zero, we are on a frictionless surface. Therefore, any force of any magnitude can accelerate the object resting on such a surface.
Problem (4): A heavy block weighing $300\,{\rm N}$ is moved at a constant speed by a force of $45\,{\rm N}$ applied parallel to the motion.
(a) What is the coefficient of friction involved in the problem?
(b) What is the mass of the block?
(c) Assuming $\mu_k=0$, find the acceleration of the block?
Solution: The weight of the block $W=mg=300\,{\rm N}$ and the magnitude of the external force are given.
(a) Again ''constant speed''. If there is a force equal in magnitude but opposite in direction of the external force, then the net force on the object is zero and, as a result, it moves at a constant speed.
Therefore, the friction force must be equal to the magnitude of the external force, $F=f_k=\mu_k F_N$. The block is moving, so we are dealing with kinetic friction.
In the vertical direction there is no motion, so Newton's second law of motion in this direction, $F_{net-y}=ma_y$, which gives us the magnitude of the normal force \[F_N-mg=0 \Rightarrow F_N=mg=300\,{\rm N}\] Now solving $F=f_k=\mu_k F_N$ for $\mu_k$, we have \[\mu_k=\frac{F}{F_N}=\frac{45}{300}=0.15\]
(b) Using the definition of weight in physics, $W=mg$, and solving this for $m$, we get \[m=\frac{W}{g}=\frac{300}{10}=30\,{\rm kg}\]
(c) In the case of zero friction, $\mu_k=0$, any force, no matter how small, accelerates the body whose magnitude is found as below \[a=\frac{F}{m}=\frac{45}{30}=1.5\,{\rm m/s^2}\]
Problem (5): A force of $35\,{\rm N}$ parallel to a concrete surface is required to start a $6\,{\rm kg}$ block resting on the surface to move.
(a) What is the coefficient of static friction between the block and the surface?
(b) By maintaining this force, the block accelerates at a constant rate of $0.6\,{\rm m/s^2}$. What is the coefficient of kinetic friction?
Solution: static friction does not have a simple formula. This type of friction varies with the external force acting on an object. But there is an upper bound for it, beyond which the object starts to move from rest.
The magnitude of static friction force at this particular instant, when the static friction has its greatest value, is determined by the formula \[f_{s, max}=\mu_s F_N\]
(a) The block is on a horizontal surface and an external force parallel to the surface acts on it, so the normal force equals the object's weight: \[F_N=mg=6\times 10=60\,{\rm N}\] In the problem, we were told that the object is at rest and wants to be on the verge of sliding. So, the only friction force involved in the movement is the static friction, whose maximum value is $f_{s, max}=\mu_s F_N$.
As said, the maximum value of static friction is always equal to the external forces acting on the object.
In this case, a $35-{\rm N}$ force puts the object on the verge of motion. So, $F=f_{s,max}$. Solving this equation for $\mu_s$, we find the coefficient of static friction as \begin{align*} f_{s,max}&=F\\\\ \mu_s F_N&=F\\\\ \Rightarrow \mu_s&=\frac{F}{F_N}\\\\&=\frac{35}{70}=0.5\end{align*}
(b) If this constant force continues, the object will move and the kinetic friction force will be exerted on the object.
Because it is said that the block experiences acceleration, there must be a net force on it. The external force is along the direction of motion, and by definition, the friction force is always in the opposite direction of motion.
Thus, the net force on the block is found by subtracting the friction from the external force as below: \[F_{net}=F-f_k=F-\mu_k F_N\] The block is on a horizontal surface with a force applied to it horizontally, so the normal force is always $F_N=mg=7\times 10=70\,{\rm N}$. According to Newton's second law, $F_{net}=ma$. Combining these two last equations, and solving for $\mu_k$, we have \begin{gather*} F_{net}=ma\\\\ F-\mu_k (mg)=ma \\\\ \Rightarrow \mu_k=\frac{F-ma}{mg} \\\\ =\frac{35-7\times 0.6}{7\times 10}\\\\=0.44\end{gather*} As expected, since always $\mu_s>\mu_k$.
Problem (6): A $20-{\rm kg}$ crate is initially at rest on a surface. A force of $75\,{\rm N}$ sets the crate in motion. After moving, a $60-{\rm N}$ force is required to keep it moving with a constant speed. What are the static and kinetic coefficients of friction between the crate and the surface?
Solution: In this question, we are given two external forces, one sets the crate in motion $F_1$, and the other keeps it moving at a constant speed $F_2$.
In all problems involving the coefficient of friction, that force that sets the object in motion from rest is associated with the maximum force of static friction whose magnitude is given by formula $f_{s, max}=\mu_s F_N$.
Therefore, the force $F_1$ is the maximum external force that is needed to overcome the static friction, so we can find the coefficient of static friction as \begin{align*} F_1&=f_{s,\max}=\mu_s F_N\\\\ F_1&=\mu_s (mg) \\\\75&=\mu_s (20\times 10) \\\\ \Rightarrow \mu_s &=\frac{75}{200} \\\\ &=0.375\end{align*} The friction force that is applied to a moving body is the kinetic friction force. In this case, a constant force of $60\,{\rm N}$, keeps the motion with constant speed. So, using kinetic friction force formula $f_k=\mu_k F_N$ and solving for $\mu_k$, we have \begin{align*} F_2&=f_k=\mu_k F_N\\\\ F_2&=\mu_2 (mg) \\\\60&=\mu_k (20\times 10) \\\\ \Rightarrow \mu_s &=\frac{60}{200} \\\\ &=0.300\end{align*} As expected, $\mu_s>\mu_k$.
Problem (7): A block is sitting on the surface of a moving train accelerating at $0.2g$. What minimum coefficient of static friction must exist between the block and the train's surface so that the block is not to slide?
Solution: A force in the direction of the train's acceleration is applied to the block. This force wants to displace the block but we want it not to happen. Thus, a force in the opposite direction of the external force must be exerted on the block to stop it from sliding.
This force that opposes the sliding of an object at rest is static friction. Thus, in this case, if the applied force by the acceleration of the train is canceled by the static friction, then the block does not slide on the surface. Hence, we have \begin{align*} F_{train}&=f_{s,max}\\\\ F_{train}&=\mu_s F_N \\\\ m_{block}a_{train}&=\mu_s (m_{block}g) \\\\ m_{block}(0.2g)&=\mu_s (m_{block}g) \\\\ \Rightarrow \mu_s &=0.2\end{align*} In the above, $F_N$ is the normal force exerted by the surface.
Problem (8): A block weighing $20\,{\rm N}$ is pulled by a rope horizontally along a surface. Assume the coefficients of static and kinetic friction between the block and the surface are $\mu_s=0.8$ and $\mu_k=0.6$. Find the magnitude of the force of friction on the block if
(a) The block is pulled by a tension force of $15\,{\rm N}$.
(b) The block is pulled by a tension force of $20\,{\rm N}$.
Solution: First, draw a free-body diagram and specify all forces acting on the block.
The object does not move in the vertical direction, so Newton's second law gives us the magnitude of the normal force exerted by the surface: \[F_N-mg=0 \Rightarrow F_N=mg=20\,{\rm N}\] We don't know whether the block moves or not. We know only if the applied force is greater than the maximum of static friction, then the block will move, otherwise, the object remains at rest.
On the other hand, if the applied force causes the object to move, then the friction is of the kinetic type; otherwise, it is static.
With these explanations, we must first find the maximum static friction, $f_{s, max}=\mu_s F_N$, that is applied to the block on this such surface. \[f_{s,max}=\mu_s F_N=0.8\times 20=16\,{\rm N}\] Note that this is the maximum value that the static friction can accept. Its value, at any instant, is determined by the amount of externally applied force.
(a) In this case, the applied force is not sufficient to overcome the maximum static friction force, so the object will not move. Hence, the static friction at that moment must be equal to the external force, i.e. \[f_s=F=20\,{\rm N}\]
(b) Now, the external force is as much as that can overcome the maximum of the static friction, $F>f_{s, max}$, so the object will move. When the object moves, instead of static friction, the force of kinetic friction opposes the motion whose magnitude is obtained as \[f_k=\mu_k F_N=0.6\times 20=12\,{\rm N}\]
Problem (9): A crate of mass $m$ is pulled at a constant velocity across a rough surface by a rope inclined at $\alpha$. What is the magnitude of the frictional force on the crate?
Solution: The block is moving on the surface, so we are dealing with kinetic friction force whose magnitude is $f_k=\mu_k F_N$. Thus, we need the magnitude of the normal force exerted by the surface to find the friction.
First, we draw a free-body diagram to explicitly see the forces applying to the crate.
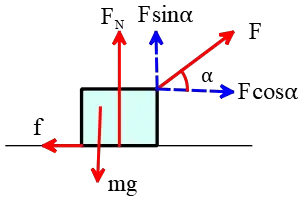
Resolving the tension force in the rope, two extra forces appear in the horizontal and vertical directions (blue dotted arrows). In the vertical direction, there is no motion $a_y=0$, so the net force vertically must be zero $F_{net,y}=ma_y=0$. Consider the positive direction upward. Thus, by equating the net force for vertical direction ($y$) zero, the normal force is obtained \begin{gather*}F_N+F\sin\alpha-mg=0 \\\\ \Rightarrow F_N=mg-F\sin\alpha \end{gather*} Now, substitute the normal force into the kinetic friction formula, to find its magnitude \[f_k=\mu_k F_N=\mu_k (mg-F\sin\alpha)\]
To practice more on resolving a vector in physics, refer to the following page:
Definition of vector in physics
Problem (10): Consider the coefficient of kinetic friction between tires and a horizontal road surface is $0.6$.
(a) In the case of braking, what is the magnitude of the maximum acceleration the car obtains?
(b) Assume the car initially travels at $30\,{\rm m/s}$. Determine the shortest distance in which the car can stop.
Solution: (a) When the car is braked, the only applied force along the motion is the kinetic friction, but in the opposite direction (see figure).
Applying Newton's second law in the $x$-direction, we will have \begin{align*} F-f_k&=ma\\ 0-\mu_k F_N &=ma \\ \mu_k(mg)&=ma\\ \Rightarrow a&=-\mu_k g\\&=(0.6)(10) \\&=-6\quad {\rm m/s^2}\end{align*}
(b) This part is related to the kinematics problems. We can use the time-independent kinematic equation $v^2-v_0^2=2a\Delta x$ to find the distance traveled by car during braking.
Substitute $v=0$, $v_0=30\,{\rm m/s}$, and $a=-6\,{\rm m/s^2}$. \begin{align*} a&=\frac{v^2-v_0^2}{2\Delta x}\\\\&=\frac{0-(30)^2}{2(6)}\\\\&=75\quad {\rm m}\end{align*}
Coefficient of static friction: Problems
Problem (11): A $100\,{\rm N}$ is applied to a $50\,{\rm kg}$ box setting on a surface. Suppose the coefficient of static friction is $\mu_s=0.25$. Is this applied force enough to move the box?
Solution: As mentioned earlier, for static friction, we can only find its maximum value, in contrast to kinetic friction. At any other moment, before reaching the maximum value, this is the external force that determines the magnitude of the static friction.
If the externally applied force on an object is less than the maximum of the static friction $F<f_{s, max}$, then the static friction equals the magnitude of the external force, $f_s=F$.
In this case, first, find the maximum value of the static friction \[f_{s, max}=\mu_s F_N=0.25\times 500=125\,{\rm N}\] where we substituted $mg$ for the normal force since the object is on a horizontal surface and a horizontal force is applied to it.
As you can see, the applied external force is not enough to move the object since $F<f_{s, max}$. So, the magnitude of the static friction is $f_s=100\,{\rm N}$.
Problem (12): A $300\,{\rm N}$ is required to start a box to move over a rough-level floor. If the coefficient of static friction between them is $0.35$, find the mass of the box.
Solution: The box is initially at rest, and a force of $300\,{\rm N}$ puts it on the verge of motion. So, this external force must be enough to overcome the maximum force of static friction, $F=f_{s, max}=\mu_s F_N$.
The object does not move in the vertical direction, so the net force vertically must be zero, \[F_N-mg=0 \Rightarrow F_N=mg\] Substituting this into the above expression and solving for $m$, we will have \begin{align*} F&=\mu_s F_N=\mu_s (mg) \\\\ \Rightarrow m&=\frac{F}{\mu_s g}\\\\ &=\frac{300}{0.35\times 10}\\\\ &=85.7\quad {\rm kg} \end{align*}
Problem (13): How much horizontal force is needed to start an $850-{\rm kg}$ crate sliding across a surface if the coefficient of static friction between the box and the surface is $0.45$?
Solution: In all coefficient of friction problems, we need to know the normal force on the object. As a rule of thumb, if the object is on a horizontal surface and a force parallel to the surface is applied to it, then Newton's second law tells us that the normal force is equal to the weight force mg, $F_N=mg$.
Now we turn to the main question. The crate is initially at rest. The maximum force of static friction applied to it is \begin{align*} f_{s,max}&=\mu_s F_N\\&=(0.45)(850\times 10) \\&=3825\quad {\rm N}\end{align*} If the externally applied force exceeds this value, then the object starts to move. Therefore, a force of $3825\,{\rm N}$ to an $850\,{\rm kg}$ on such a surface, can put the crate on the verge of sliding.
Problem (14): The coefficient of static friction between the tires of a car and a street asphalt surface is $0.9$. How steep can you park your car on a hill (maximum angle)?
Solution: First, draw a free-body diagram and specify all forces acting on the car.
The weight force of an object on an incline always resolves into two components: one is parallel to the incline downward $mg\sin\alpha$, and the other is perpendicular to the incline, $mg\cos\alpha$, as shown in the free-body diagram.
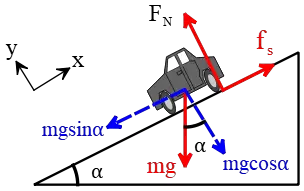
Applying Newton's second law of motion in the vertical direction to the motion gives us the normal force on the car. The car's acceleration vertically is zero $a_y=0$, so the net force in this direction must be zero $F_{net,y}=ma_y=0$. \[F_N-mg\cos\alpha=0 \Rightarrow F_N=mg\cos\alpha\] In this case, we want the car to remain at rest on an incline of angle $\alpha$. Thus, we need a static friction force (since the car is not moving instead of kinetic friction) with the same magnitude but in the opposite direction of $mg\sin\alpha$ to cancel it out.
By solving this expression for $\mu_s$, we get \begin{align*} mg\sin\alpha&=\mu_s F_N\\ mg\sin\alpha&=\mu_s(mg\cos\alpha)\\\\ \Rightarrow \mu_s&=\frac{\sin\alpha}{\cos\alpha}=\tan\alpha\end{align*} To park the car on an inclined street, the coefficient of static friction must be equal to the tangent of the angle of incline. Taking the inverse of tangent, we can find the desired angle \[\alpha=\tan^{-1}(\mu_s)=\tan^{-1}(0.9)\approx 42^\circ\] This is a general rule and one of the methods to find the coefficient of static friction.
Summary:
In this tutorial, you learned how to use the coefficient of friction to solve friction problems in physics.
Overall, to find the friction force in a problem, you must first determine the normal force on the object. Then, recognize which friction force, static or kinetic, is involved in the question.
In the end, substitute the given numerical values to find the desired quantity.
Author: Dr. Ali Nemati
Page Published: 9/30/2021
© 2015 All rights reserved. by Physexams.com
