Refractive Index: Formula and Solved Problems
In this tutorial, the index of refraction formula is explored with several solved sample problems. All these problems are simple and useful for high schools.
In physics, the ratio of the speed of light in a vacuum to the speed of light in a medium is called the index of refraction. The formula of index of refraction is written as \begin{gather*} n=\frac{\text{Speed of light in a vacuum}}{\text{Speed of light in the medium}}\\\\ n=\frac{c}{v_{medium}}\end{gather*}
Index of Refraction Formula: Definition
When light travels from one medium into another, it is refracted because the speed of light is different in the two media.
The index of refraction shows a kind of strength of a substance in refracting the incident light.
In the following sample problems, we see that the higher the index of refraction, the slower the speed of light in a material.
On the other side, the lower the speed of light in a substance, the smaller the angle of refraction.
Let's solve a few problems on the index of refraction.
Problem (1): The speed of a ray of light in ice is $2.29\times 10^{8}\,{\rm m/s}$. Find the index of refraction of ice.
Solution: The index of refraction of a transparent material, $n$, is defined as the speed of light in the vacuum divided by the speed of light in that material. \[n=\frac{c}{v}\] Note that $v$ is the speed of light in that medium. Substituting the numerical values into the index of refraction formula, we get \[n_{ice}=\frac{c}{v_{ice}}=\frac{3\times 10^{8}}{2.29\times 10^{8}}=1.31\] The index of refraction is a dimensionless quantity in physics.
Problem (2): The index of refraction of a medium is measured to be 1.2. What is the speed of light through that medium?
Solution: The speed of light moving through a dense medium is found using the formula \[n=\frac{c}{v}\] Rearranging this and solving for $v$, we can find the speed of light in a medium. \[v=\frac{c}{n}=\frac{3\times 10^8}{1.2}=2\times 10^8\quad {\rm m/s}\] Pay attention that the speed of light in vacuum is the maximum speed in nature and consequently, $v$ is always less than $c$.
Problem (3): The speed of light in a particular transparent medium is $82\%$ of its value in water. What is the index of refraction of this medium? (The index of refraction of water is 1.33)
Solution: The speed of light in a transparent material is determined by the formula $v=\frac{c}{n}$. Here, we are told that the speed of light in an unknown material $v_u$ is $82\%$ of its value in water so $v_u=0.82v_w$. Applying the above formula, we will have \begin{align*} \frac{c}{n_u}&=0.82\,\frac{c}{n_w}\\\\ \Rightarrow \quad n_w&=0.82 n_u\end{align*} So, the refractive index of the unknown medium is found to be \[n_u=\frac{n_w}{0.82}=\frac{1.33}{0.82}=1.62\]
Problem (4): A beam of light of wavelength $589\,{\rm nm}$ in the vacuum passes through a piece of Silicon of the index of refraction $n=3.5$.
(a) How fast does light travel in Silicon?
(b) How does the wavelength of light change in Silicon?
(c) What is the frequency of light in Silicon?
Solution: When light traveling in one medium enters the second medium, its velocity is changed. This change in velocity is the basic principle of refraction in physics.
(a) The ratio of the speed of light in the vacuum to the speed in a transparent medium is defined as the index of refraction of that medium i.e. $n=\frac{c}{v}$. Solving this equation for $v$, we have \[v=\frac{c}{n}=\frac{3\times 10^8}{3.5}=8.57\times 10^7\,{\rm m/s}\]
(b) In a similar way, when light moves from one medium into another, its wavelength also changes. In particular, when a beam of light of wavelength $\lambda_0$ in the vacuum passes through a dense medium having a refractive index of $n$, its wavelength reduces by the amount of \[\lambda_n=\frac{\lambda_0}{n}\] where $\lambda_n$ is the wavelength in the medium having index of refraction $n$. With these explanations, we have \[\lambda_n=\frac{589\,{\rm nm}}{3.5}=168.3\quad {\rm nm}\]
(c) As light travels from one medium to the second one, its frequency does not change. The only things that change when a wave moves from one medium to another are wavelength and speed in the medium.
So, the frequency of this ray of light in Silicon is the same as in the vacuum. To find the frequency, we use the wave speed formula $v=f\lambda$. In the vacuum $v=c$ so $c=\lambda f$. Thus, the frequency in of light in Silicon is found to be \[f=\frac{c}{\lambda}=\frac{3\times 10^8\,{\rm m/s}}{589\times 10^{-9}}\,{\rm m}=5.09\times 10^{14}\,{\rm Hz}\]
Problem (5): The index of refraction of diamond $n=2.41$. What is the speed of light through the diamond?
Solution: According to the definition of the index of refraction, $n=\frac{c}{v}$, the speed of a light ray in a medium, say diamond, is measured to be \[v=\frac{c}{n}=\frac{3\times 10^8}{2.41}=1.25\times 10^8\quad {\rm m/s}\] As expected because the speed of light in a medium is always less than the speed in the vacuum $c$.
Problem (6): A ray of red light takes $2.63\,{\rm ns}$ to travel $50\,{\rm cm}$ through an optically dense medium. What is the index of refraction of this medium?
Solution: This problem involves a kinematics problem. The known information is the time taken $t$ and distance traveled $d$ in the medium. Recall that the ratio of distance traveled to the time taken is the definition of speed in physics, $v=\frac{d}{t}$.
This light ray is moving in a dense medium so its speed can be related to the index of refraction of that medium using equation $n=\frac{c}{v}$. Combining these two above equations, and solving for the unknown $n$, we get \begin{align*} v&=\frac{d}{t}=\frac{c}{n}\\\\ \Rightarrow \quad n&=\frac{ct}{d}\\\\ &=\frac{(3\times 10^8)(2.63\times 10^{-9})}{0.5}\\\\&=1.578\end{align*}
Problem (7): The index of refraction for crown glass is $1.52$. A beam of light of wavelength $6500\text{\AA}$ in a vacuum passes through it. What is the wavelength of this light in the crown glass?
Solution: When a light of wavelength $\lambda_0$ in a vacuum moves through a dense medium having a refractive index of $n$, its wavelength in that medium is found to be $\lambda_n=\frac{\lambda_0}{n}$. Using this formula, we have \[\lambda_n=\frac{6500}{1.52}=4276.3 \text{\AA} \] As expected, the wavelength in a dense medium is reduced.
Problem (8): A ray of light having wavelength $\lambda$ in a vacuum enters three different transparent mediums. From largest to smallest, rank the indices of refraction of the media.
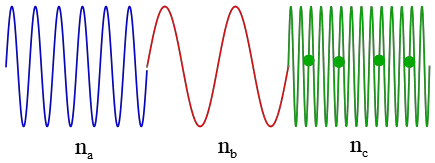
Solution: The extension of the wavelength of light in each medium is shown. As you can see, the wavelength in $b$ is greater than $a$ than $c$. \[\lambda_b>\lambda_a>\lambda_c\] According to the refractive index formula for wavelength, $\lambda_n=\frac{\lambda}{n}$, the wavelength in any transparent medium is inversely proportional with the index of refraction of that medium. So, the larger the wavelength, the greater the index of refraction. Hence, the order of the indices of refraction for the given mediums is as follows \[n_c>n_a>n_b\]
Problem (9): Two data centers, 300-m away, are connected with each other through optical fibers having a refractive index of 1.55. How long does it take the light to travel through this optical fiber?
Solution: The distance traveled $d=300\,{\rm m}$ and the index of refraction of the optical fiber $n=1.55$ are given. The refractive index formula,$n=\frac{c}{v}$, tells us about the velocity of a light ray in a medium like optical fiber. Having speed and distance traveled, we can use the definition of speed, $v=\frac{d}{t}$, to find the time elapsed.
Combining these two equations, gives us \[n=\frac{c}{d/t}=\frac{ct}{d}\] Solving this for $t$ and substituting the numerical values we will have \begin{align*} t&=\frac{nd}{c}\\\\&=\frac{(1.55)(300)}{3\times 10^{8}}\\\\&=1.55\times 10^{-6}\quad{\rm s}\end{align*} So, it takes about $1.5\,{\rm \mu s}$ to light travels this distance between the data centers.
Index of Refraction Formula in Snell's law
Another method to find the index of refraction of a material is using Snell's law of refraction. According to this rule, when a ray of light, strikes at an angle of $\theta_1$ with normal upon a boundary of another medium, it is refracted and enters into the second medium at an angle of $\theta_2$ with normal.
The first angle is called the angle of incidence and the second one is the angle of refraction. Snell's law relates these two angles with each other using the following formula \[n_1 \sin\theta_1=n_2 \sin\theta_2\] where $n_1$ and $n_2$ are the indices of refractive of the corresponding media.
Suppose a light ray is in the air and is to enter an unknown material. Knowing the angles of incidence and refraction, we can use this equation to find the index of refraction of that material.
In the following, we use Snell's law to find the index of refraction using some worked sample problems.
Problem (10): A ray of light traveling in the air, strikes the boundary of an unknown transparent material at an angle of incidence $54^\circ$. The angle of refraction is $23^\circ$. What is the index of refraction of that material?
Solution: When a light ray travels through a medium and strikes the boundary of another medium, it is refracted and bends toward or away from the normal. Snell's law of refraction governs this behavior. According to this rule, $n_1 \sin\theta_1=n_2\sin \theta_2$, where $\theta_1$ and $\theta_2$ are the angles of incidence and refraction with normal.
Substituting the numerical values into Snell's law formula and solving for the refractive index of unknown material, we have \begin{align*} n_1 \sin\theta_1&=n_2\sin \theta_2\\\\ (1)\sin 53^\circ&=n_2\sin 23^\circ\\\\ 0.8&=(0.39)n_2\\\\ \Rightarrow n_2&= 2.05 \end{align*}
To practice more problems on Snell's law, refer to the following page:
Snell's law Problems with answers
Problem (11): An unknown material is surrounded by water. A ray of the yellow light of wavelength $589\,{\rm nm}$ strikes the boundary between them at $45^\circ$ and is refracted at $32^\circ$. What is the index of refraction of the material? (The refractive index of water is 1.33).
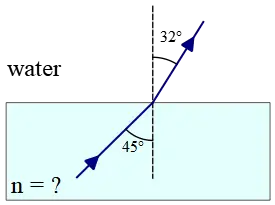
Solution: The angle of incidence $\theta_1=45^\circ$ and of refraction $\theta_2=32^\circ$ are given. Using Snell's law, we can a formula for index of refraction of that medium \begin{align*} n_1 \sin\theta_1&=n_2\sin \theta_2\\\\ (1.33)\sin 45^\circ&=n_2\sin 32^\circ\\\\ (1.33)(0.707)&=(0.530)n_2\\\\ \Rightarrow n_2&= 1.774 \end{align*} As you have seen, by measuring the incident and refracted angles of a light ray strike the boundary between two different media and using Snell's law, one can find a useful equation for the index of refraction of an unknown substance.
Problem (12): What is the critical angle for total internal reflection for a beam of light leaving the crown glass and entering the air? (The refractive index of crown glass is 1.52)
Solution: Critical angle is the incident angle at which the angle of refraction is $90^\circ$. So, putting this into Snell's law we will have \begin{align*}n_1 \sin\theta_1&=n_2\sin\theta_2\\\\ (1.52)\sin\theta_1&=(1)\sin 90^\circ\\\\ \Rightarrow \quad \sin\theta_1&=\frac{1}{1.52}\\\\&=0.658\end{align*} Taking the inverse of sine of both sides, the angle whose sine is 0.658 is obtained \[\theta_1=\sin^{-1}(0.658)=41.1^\circ\] So, the critical angle for crown glass is about $41.1^\circ$.
On the other side, total internal reflection occurs when the two conditions below are satisfied:
(i) The incident light is in a medium that has a higher refractive index.
(ii) The angle of incidence is greater than the critical angle.
So, for incident angles $\alpha>41.1^\circ$, all incoming light rays striking the glass-air boundary are reflected back into the original medium.
For more problems on total internal reflection, visit the following page
Total internal reflection problems with solution
Problem (13): A ray of light originally is in an unknown substance, at an angle of $68.4^\circ$ strike the glass having the refractive index of $n_g=1.333$. The refracted ray exit along the boundary. What is the index of refraction of the unknown substance?
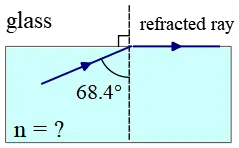
Solution: Because the refracted ray is parallel to the boundary so its angle with the normal (perpendicular) to the boundary is $\theta_2=90^\circ$. Plugging the numerical value into Snell's law of refraction and solving for $n$, we can find a formula for refractive index of the initial substance \begin{align*}n_1 \sin\theta_1&=n_2\sin\theta_2\\\\ n_1\sin 68.4^\circ&=(1.333)\sin 90^\circ\\\\ \Rightarrow \quad n_1&=\frac{1.333\times \sin 90^\circ}{\sin 68.4^\circ}\\\\&=\frac{1.333\times 1}{0.930}\\\\&=1.43\end{align*} Thus, the index of refraction of the unknown substance is $1.43$.
This particular incident angle at which the refracted ray is $90^\circ$ is called the critical angle. In this problem, if the incident angle becomes greater than this critical one, $100\%$ of the light ray is reflected back (total internal reflection) into the original substance without any part of it entering the glass.
In fact, in this situation, the boundary acts as a perfect mirror.
Summary:
In this article, the formula for the refractive index,$n$, of a material is discussed using a problem-solving strategy.
We learned that:
According to the index of refraction formula, $n=\frac{c}{v}$, the index of refraction of any substance is always greater than or equal to one. This is because the speed of light in a medium is always less than $c$.
As light travels from one medium into another, its frequency does not change but its wavelength changes as $\lambda_n=\frac{\lambda}{n}$, where $\lambda$ is the wavelength in the vacuum.
Using the refractive index formula, we can write Snell's law in an alternative form below \[n_1 \lambda_1=n_2\lambda_2\]
If light moves from one medium into another where its speed is greater, then the refracted ray bends away from the normal. This is the case for light traveling from water to air.
Author: Ali Nemati
Date Published: 9/15/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
