The helical path is the path of the motion of a charged particle when enters at an angle of $\theta$ in a uniform magnetic field $B$.
In this short tutorial, we explain the factors that cause this type of motion.
On a moving charged particle in a uniform magnetic field, a magnetic force of magnitude $F_B=qvB\,\sin \theta$ is acted where $\theta$ is the angle of velocity vector $v$ with the magnetic field vector $B$.
This is the main factor that creates a spiral or helical path.
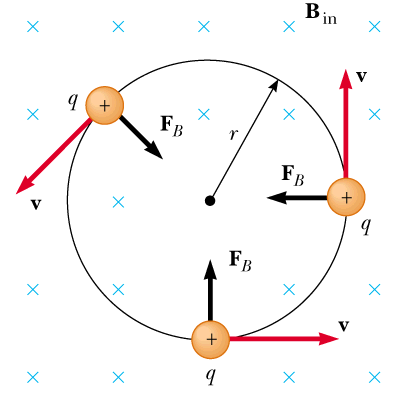
A charged particle (say, electron) can enter a region filled with uniform $B$ either with right angle $\theta=90^\circ$ or at angle $\theta$.
In the former case, its path results in a circular path, and in the latter case, a helical path is formed.
Now we want to answer this question: why do charged particles move in a helical path?
As soon as a charged particle enters a magnetic field $B$ with some angle $\theta$, one can decompose its velocity into parallel and vertical components with respect to magnetic field vector $B$ which are $v_{\parallel}=v\,\cos \theta$ and $v_{\bot}=v\,\sin \theta$.
The uniform magnetic field $B$ does not apply any force on the charged particle (say, electron) in the parallel direction since $\theta=0$ so $F_{\parallel}=q\,v_{\parallel}\,B\sin 0=0$.
Thus, the charged particle continues to move along the field direction with a uniform motion (a motion in which speed and velocity are constant ).
On the other hand, the vertical component undergoes a magnetic force of magnitude $F_{\bot}=q\,v_{\bot}\,B\sin 90^{\circ}=q\,v_{\bot}\,B$ which causes the charged particle moves uniformly around a circular path.
Those two above motions, uniform motion parallel to the field $B$ and uniform circular motion perpendicular to the field $B$, create the actual path of a charged particle in a uniform magnetic field $B$ which is similar to a spring and is called a spiral or helical path.
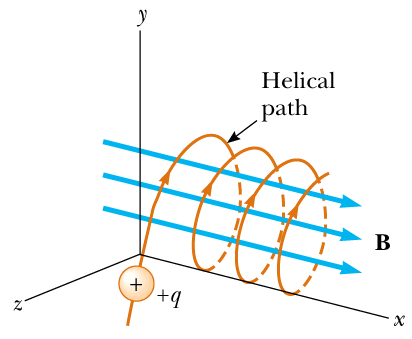
Characteristics of Helical Path:
Every helical path has three distinct characteristics as radius, time period, and pitch.
Radius: The normal force $F_{\bot}$ which creates a circular motion provides a centripetal force on the charged particle with a radial acceleration $a_r=\frac{m\,v_{\bot}^{2}}R$.
Applying Newton's second law of motion and balancing the centripetal force with the magnetic force we get a formula for the radius of the helical path as \begin{align*} F&=m\,a_r\\ \\ q\,v_{\bot}\,B&=m\,\frac{v_{\bot}^{2}}R\\ \\ \Rightarrow R&=\frac{m\,v_{\bot}}{q\,B}\\ \\&=\frac{mv\,\sin\theta}{qB}\end{align*} Where $m$ is the mass of the charged particle.
Time period: The time needed to complete one revolution is obtained by definition of average velocity as \begin{align*} v&=\frac{\Delta x}{\Delta t}\\ \\ v_{\bot}&=\frac{2\pi\,R}{T}\\ \\ \Rightarrow T&=\frac{2\pi\,R}{v_{\bot}}\\ \\&=\frac{2\pi}{q\,B}\,m\end{align*} where in the above we used the preceding formula for $R$ and $v_{\bot}=v\,\sin \theta$. This period is also called the cyclotron period and its frequency is the reciprocal of the period with formula \[f=\frac 1T=\frac{q\,B}{2\pi\,m}\]
Pitch of the helix: the distance traveled parallel to the magnetic field $B$ in one revolution is called the pitch of the helical path and is obtained as \begin{align*} p&=v_{\parallel}\,T\\&=(v\,\cos \theta)\,\left(\frac{2\pi\,m}{q\,B}\right)\end{align*} Thus, the formula for the pitch of the helix is $p=\frac{2\pi\,mv\,\cos \theta}{q\,B}$.
Example of Helical Path:
An electron with a mass $9.11\times 10^{-31}\,{\rm kg}$ and charge of $1.6\times 10^{-19}\,{\rm C}$, projected into a uniform magnetic field of $0.2\,{\rm T}$ at a speed of $1.8\times 10^{6}\,{\rm m/s}$ in such a way its velocity makes an angle of $37^{\circ}$ with the field lines. Find the period, pitch, and radius of the helical path of the electron.
Solution:
Time period of the helix is given by \begin{align*}T&=\frac{2\pi\,m}{eB}\\&=\frac{2(3.14)(9.11\times 10^{-31})}{(1.6\times 10^{-19})(0.2)}\\&=1.78\times 10^{-10}\,{\rm s}\\&=0.17\,{\rm ns}\end{align*}
Pitch of the helical motion is obtained as \begin{align*} p&=\frac{2\pi\,mv\,\cos \theta}{e\,B}\\&=\frac{2(3.14)(9.11\times 10^{-31})(1.8\times 10^{6})\cos 37^{\circ}}{(1.6\times 10^{-19})(0.2)}\\&=0.257\,{\rm mm}\end{align*}
Radius of the helical path is determined as \begin{align*}R&=\frac{mv\,\sin\theta}{eB}\\&=\frac{(9.11\times 10^{-31})(1.8\times 10^{6})\,\sin 37^{\circ}}{(1.6\times 10^{-19})(0.2)}\\&=0.193\,{\rm mm}\end{align*}
Conclusion:
- A helical path is formed when a charged particle enters with an angle of $\theta$ other than $90^{\circ}$ into a uniform magnetic field. In the case of $\theta=90^{\circ}$, a circular motion is created.
- If the particle’s velocity has components parallel and perpendicular to the uniform magnetic field then it moves in a helical path.
- In the parallel case, there is no force on the particle but in the perpendicular one, there is a centripetal acceleration toward the center.
Last Update: 9/2/2020

 kinematic
kinematic
 Electrostatic
Electrostatic
 Magnetism
Magnetism