Solved Speed, Velocity, and Acceleration Problems
Simple problems on speed, velocity, and acceleration with descriptive answers are presented for the AP Physics 1 exam and college students. In each solution, you can find a brief tutorial.
Speed and velocity Problems:
Problem (1): What is the speed of a rocket that travels $8000\,{\rm m}$ in $13\,{\rm s}$?
Solution: Speed is defined in physics as the total distance divided by the elapsed time, so the rocket's speed is \[\text{speed}=\frac{8000}{13}=615.38\,{\rm m/s}\]
Problem (2): How long will it take if you travel $400\,{\rm km}$ with an average speed of $100\,{\rm m/s}$?
Solution: Average speed is the ratio of the total distance to the total time. Thus, the elapsed time is \begin{align*} t&=\frac{\text{total distance}}{\text{average speed}}\\ \\ &=\frac{400\times 10^{3}\,{\rm m}}{100\,{\rm m/s}}\\ \\ &=4000\,{\rm s}\end{align*} To convert it to hours, it must be divided by $3600\,{\rm s}$ which gives $t=1.11\,{\rm h}$.
Problem (3): A person walks $100\,{\rm m}$ in $5$ minutes, then $200\,{\rm m}$ in $7$ minutes, and finally $50\,{\rm m}$ in $4$ minutes. Find its average speed.
Solution: First find its total distance traveled ($D$) by summing all distances in each section, which gets $D=100+200+50=350\,{\rm m}$. Now, by definition of average speed, divide it by the total time elapsed $T=5+7+4=16$ minutes.
But keep in mind that since the distance is in SI units, so the time traveled must also be in SI units, which is $\rm s$. Therefore, we have\begin{align*}\text{average speed}&=\frac{\text{total distance} }{\text{total time} }\\ \\ &=\frac{350\,{\rm m}}{16\times 60\,{\rm s}}\\ \\&=0.36\,{\rm m/s}\end{align*}
Problem (4): A person walks $750\,{\rm m}$ due north, then $250\,{\rm m}$ due east. If the entire walk takes $12$ minutes, find the person's average velocity.
Solution: Average velocity, $\bar{v}=\frac{\Delta x}{\Delta t}$, is displacement divided by the elapsed time. Displacement is also a vector that obeys the addition vector rules. Thus, in this velocity problem, add each displacement to get the total displacement.
In the first part, displacement is $\Delta x_1=750\,\hat{j}$ (due north) and in the second part $\Delta x_2=250\,\hat{i}$ (due east). The total displacement vector is $\Delta x=\Delta x_1+\Delta x_2=750\,\hat{i}+250\,\hat{j}$ with magnitude of \begin{align*}|\Delta x|&=\sqrt{(750)^{2}+(250)^{2}}\\ \\&=790.5\,{\rm m}\end{align*} In addition, the total elapsed time is $t=12\times 60$ seconds. Therefore, the magnitude of the average velocity is \[\bar{v}=\frac{790.5}{12\times 60}=1.09\,{\rm m/s}\]
Problem (5): An object moves along a straight line. First, it travels at a velocity of $12\,{\rm m/s}$ for $5\,{\rm s}$ and then continues in the same direction with $20\,{\rm m/s}$ for $3\,{\rm s}$. What is its average speed?
Solution: Average velocity is displacement divided by elapsed time, i.e., $\bar{v}\equiv \frac{\Delta x_{tot}}{\Delta t_{tot}}$.
Here, the object goes through two stages with two different displacements, so add them to find the total displacement. Thus,\[\bar{v}=\frac{x_1 + x_2}{t_1 +t_2}\] Again, to find the displacement, we use the same equation as the average velocity formula, i.e., $x=vt$. Thus, displacements are obtained as $x_1=v_1\,t_1=12\times 5=60\,{\rm m}$ and $x_2=v_2\,t_2=20\times 3=60\,{\rm m}$. Therefore, we have \begin{align*} \bar{v}&=\frac{x_1+x_2}{t_1+t_2}\\ \\&=\frac{60+60}{5+3}\\ \\&=\boxed{15\,{\rm m/s}}\end{align*}
Problem (6): A plane flies the distance between two cities in $1$ hour and $30$ minutes with a velocity of $900\,{\rm km/h}$. Another plane covers that distance at $600\,{\rm km/h}$. What is the flight time of the second plane?
Solution: first find the distance between two cities using the average velocity formula $\bar{v}=\frac{\Delta x}{\Delta t}$ as below \begin{align*} x&=vt\\&=900\times 1.5\\&=1350\,{\rm km}\end{align*} where we wrote one hour and a half minutes as $1.5\,\rm h$. Now use again the same kinematic equation above to find the time required for another plane \begin{align*} t&=\frac xv\\ \\ &=\frac{1350\,\rm km}{600\,\rm km/h}\\ \\&=2.25\,{\rm h}\end{align*} Thus, the time for the second plane is $2$ hours and $0.25$ of an hour, which converts to minutes as $2$ hours and ($0.25\times 60=15$) minutes.
Problem (7): To reach a park located south of his jogging path, Henry runs along a 15-kilometer route. If he completes the journey in 1.5 hours, determine his speed and velocity.
Solution: Henry travels his route to the park without changing direction along a straight line. Therefore, the total distance traveled in one direction equals the displacement, i.e, \[\text{distance traveled}=\Delta x=15\,\rm km\]Velocity is displacement divided by the time of travel \begin{align*} \text{velocity}&=\frac{\text{displacement}}{\text{time of travel}} \\\\ &=\frac{15\,\rm km}{1.5\,\rm h} \\\\ &=\boxed{10\,\rm km/h}\end{align*} and by definition, its average speed is \begin{align*} \text{speed}&=\frac{\text{distance covered}}{\text{time interval}}\\\\&=\frac{15\,\rm km}{1.5\,\rm h}\\\\&=\boxed{10\,\rm km/h}\end{align*} Thus, Henry's velocity is $10\,\rm km/h$ to the south, and its speed is $10\,\rm km/h$. As you can see, speed is simply a positive number, with units but velocity specifies the direction in which the object is moving.
Problem (8): In 15 seconds, a football player covers the distance from his team's goal line to the opposing team's goal line and back to the midway point of the field having 100-yard-length. Find, (a) his average speed, and (b) the magnitude of the average velocity.
Solution: The total length of the football field is $100$ yards or in meters, $L=91.44\,\rm m$. Going from one goal's line to the other and back to the midpoint of the field takes $15\,\rm s$ and covers a distance of $D=100+50=150\,\rm yd$.
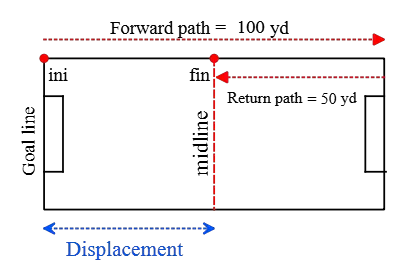
Distance divided by the time of travel gets the average speed, \[\text{speed}=\frac{150\times 0.91}{15}=9.1\,\rm m/s\] To find the average velocity, we must find the displacement of the player between the initial and final points.
The initial point is her own goal line and her final position is the midpoint of the field, so she has displaced a distance of $\Delta x=50\,\rm yd$ or $\Delta x=50\times 0.91=45.5\,\rm m$. Therefore, her velocity is calculated as follows \begin{align*} \text{velocity}&=\frac{\text{displacement}}{\text{time elapsed}} \\\\ &=\frac{45.5\,\rm m}{15\,\rm s} \\\\&=\boxed{3.03\quad \rm m/s}\end{align*} Contrary to the previous problem, here the motion is not in one direction, hence, the displacement is not equal to the distance traveled. Accordingly, the average speed is not equal to the magnitude of the average velocity.
Problem (9): You begin at a pillar and run towards the east (the positive $x$ direction) for $250\,\rm m$ at an average speed of $5\,\rm m/s$. After that, you run towards the west for $300\,\rm m$ at an average speed of $4\,\rm m/s$ until you reach a post. Calculate (a) your average speed from pillar to post, and (b) your average velocity from pillar to post.
Solution: First, you traveled a distance of $L_1=250\,\rm m$ toward east (or $+x$ direction) at $5\,\rm m/s$. Time of travel in this route is obtained as follows \begin{align*} t_1&=\frac{L_1}{v_1}\\\\ &=\frac{250}{5}\\\\&=50\,\rm s\end{align*} Likewise, traveling a distance of $L_2=300\,\rm m$ at $v_2=4\,\rm m/s$ takes \[t_2=\frac{300}{4}=75\,\rm s\]
(a) Average speed is defined as the distance traveled (or path length) divided by the total time of travel \begin{align*} v&=\frac{\text{path length}}{\text{time of travel}} \\\\ &=\frac{L_1+L_2}{t_1+t_2}\\\\&=\frac{250+300}{50+75} \\\\&=4.4\,\rm m/s\end{align*} Therefore, you travel between these two pillars in $125\,\rm s$ and with an average speed of $4.4\,\rm m/s$.
(b) Average velocity requires finding the displacement between those two points. In the first case, you move $250\,\rm m$ toward $+x$ direction, i.e., $L_1=+250\,\rm m$. Similarly, on the way back, you move $300\,\rm m$ toward the west ($-x$ direction) or $L_2=-300\,\rm m$. Adding these two gives us the total displacement between the initial point and the final point, \begin{align*} L&=L_1+L_2 \\\\&=(+250)+(-300) \\\\ &=-50\,\rm m\end{align*} The minus sign indicates that you are generally displaced toward the west.
Finally, the average velocity is obtained as follows: \begin{align*} \text{average velocity}&=\frac{\text{displacement}}{\text{time of travel}} \\\\ &=\frac{-50}{125} \\\\&=-0.4\,\rm m/s\end{align*} A negative average velocity indicating motion to the left along the $x$-axis.
This speed problem better makes it clear to us the difference between average speed and average speed. Unlike average speed, which is always a positive number, the average velocity in a straight line can be either positive or negative.
Problem (10): What is the average speed for the round trip of a car moving uphill at 40 km/h and then back downhill at 60 km/h?
Solution: Assuming the length of the hill to be $L$, the total distance traveled during this round trip is $2L$ since $L_{up}=L_{down}=L$. However, the time taken for going uphill and downhill was not provided. We can write them in terms of the hill's length $L$ as $t=\frac L v$.
Applying the definition of average speed gives us \begin{align*} v&=\frac{\text{distance traveled}}{\text{total time}} \\\\ &=\frac{L_{up}+L_{down}}{t_{up}+t_{down}} \\\\ &=\cfrac{2L}{\cfrac{L}{v_{up}}+\cfrac{L}{v_{down}}} \end{align*} By reorganizing this expression, we obtain a formula that is useful for solving similar problems in the AP Physics 1 exams. \[\text{average speed}=\frac{2v_{up} \times v_{down}}{v_{up}+v_{down}}\] Substituting the numerical values into this, yields \begin{align*} v&=\frac{2(40\times 60)}{40+60} \\\\ &=\boxed{48\,\rm m/s}\end{align*} What if we were asked for the average velocity instead? During this round trip, the car returns to its original position, and thus its displacement, which defines the average velocity, is zero. Therefore, \[\text{average velocity}=0\,\rm m/s\]
Acceleration Problems
Problem (9): A car moves from rest to a speed of $45\,\rm m/s$ in a time interval of $15\,\rm s$. At what rate does the car accelerate?
Solution: The car is initially at rest, $v_1=0$, and finally reaches $v_2=45\,\rm m/s$ in a time interval $\Delta t=15\,\rm s$. Average acceleration is the change in velocity, $\Delta v=v_2-v_1$, divided by the elapsed time $\Delta t$, so \[\bar{a}=\frac{45-0}{15}=\boxed{3\,\rm m/s^2} \]
Problem (10): A car moving at a velocity of $15\,{\rm m/s}$, uniformly slows down. It comes to a complete stop in $10\,{\rm s}$. What is its acceleration?
Solution: Let the car's uniform velocity be $v_1$ and its final velocity $v_2=0$. Average acceleration is the difference in velocities divided by the time taken, so we have: \begin{align*}\bar{a}&=\frac{\Delta v}{\Delta t}\\\\&=\frac{v_2-v_1}{\Delta t}\\\\&=\frac{0-15}{10}\\\\ &=\boxed{-1.5\,{\rm m/s^2}}\end{align*}The minus sign indicates the direction of the acceleration vector, which is toward the $-x$ direction.
Problem (11): A car moves from rest to a speed of $72\,{\rm km/h}$ in $4\,{\rm s}$. Find the acceleration of the car.
Solution: Known: $v_1=0$, $v_2=72\,{\rm km/h}$, $\Delta t=4\,{\rm s}$.
Average acceleration is defined as the difference in velocities divided by the time interval between those points \begin{align*}\bar{a}&=\frac{v_2-v_1}{t_2-t_1}\\\\&=\frac{20-0}{4}\\\\&=5\,{\rm m/s^2}\end{align*}
In above, we converted $\rm km/h$ to the SI unit of velocity ($\rm m/s$) as \[1\,\frac{km}{h}=\frac {1000\,m}{3600\,s}=\frac{10}{36}\, \rm m/s\] so we get
\[72\,\rm km/h=72\times \frac{10}{36}=20\,\rm m/s\]
Problem (12): A race car accelerates from an initial velocity of $v_i=10\,{\rm m/s}$ to a final velocity of $v_f = 30\,{\rm m/s}$ in a time interval of $2\,{\rm s}$. Determine its average acceleration.
Solution: A change in the velocity of an object $\Delta v$ over a time interval $\Delta t$ is defined as an average acceleration.
Known: $v_i=10\,{\rm m/s}$, $v_f = 30\,{\rm m/s}$, $\Delta t=2\,{\rm s}$.
Applying definition of average acceleration, we get \begin{align*}\bar{a}&=\frac{v_f-v_i}{\Delta t}\\&=\frac{30-10}{2}\\&=10\,{\rm m/s^2}\end{align*}
Problem (13): A motorcycle starts its trip along a straight line with a velocity of $10\,{\rm m/s}$ and ends with $20\,{\rm m/s}$ in the opposite direction in a time interval of $2\,{\rm s}$. What is the average acceleration of the car?
Solution: Known: $v_i=10\,{\rm m/s}$, $v_f=-20\,{\rm m/s}$, $\Delta t=2\,{\rm s}$, $\bar{a}=?$.
Using average acceleration definition we have \begin{align*}\bar{a}&=\frac{v_f-v_i}{\Delta t}\\\\&=\frac{(-20)-10}{2}\\\\ &=\boxed{-15\,{\rm m/s^2}}\end{align*}Recall that in the definition above, velocities are vector quantities. The final velocity is in the opposite direction from the initial velocity so a negative must be included.
Problem (14): A ball is thrown vertically up into the air by a boy. After $4$ seconds, it reaches the highest point of its path. How fast does the ball leave the boy's hand?
Solution: At the highest point, the ball has zero speed, $v_2=0$. It takes the ball $4\,\rm s$ to reach that point. In this problem, our unknown is the initial speed of the ball, $v_1=?$. Here, the ball accelerates at a constant rate of $g=-9.8\,\rm m/s^2$ in the presence of gravity.
When the ball is tossed upward, the only external force that acts on it is the gravity force.
Using the average acceleration formula $\bar{a}=\frac{\Delta v}{\Delta t}$ and substituting the numerical values into this, we will have \begin{gather*} \bar{a}=\frac{\Delta v}{\Delta t} \\\\ -9.8=\frac{0-v_1}{4} \\\\ \Rightarrow \boxed{v_1=39.2\,\rm m/s} \end{gather*} Note that $\Delta v=v_2-v_1$.
Problem (15): A child drops crumpled paper from a window. The paper hit the ground in $3\,\rm s$. What is the velocity of the crumpled paper just before it strikes the ground?
Solution: The crumpled paper is initially in the child's hand, so $v_1=0$. Let its speed just before striking be $v_2$. In this case, we have an object accelerating down in the presence of gravitational force at a constant rate of $g=-9.8\,\rm m/s^2$. Using the definition of average acceleration, we can find $v_2$ as below \begin{gather*} \bar{a}=\frac{\Delta v}{\Delta t} \\\\ -9.8=\frac{v_2-0}{3} \\\\ \Rightarrow v_2=3\times (-9.8)=\boxed{-29.4\,\rm m/s} \end{gather*} The negative shows us that the velocity must be downward, as expected!
Problem (16): A car travels along the $x$-axis for $4\,{\rm s}$ at an average velocity of $10\,{\rm m/s}$ and $2\,{\rm s}$ with an average velocity of $30\,{\rm m/s}$ and finally $4\,{\rm s}$ with an average velocity $25\,{\rm m/s}$. What is its average velocity across the whole path?
Solution: There are three different parts with different average velocities. Assume each trip is done in one dimension without changing direction. Thus, displacements associated with each segment are the same as the distance traveled in that direction and is calculated as below: \begin{align*}\Delta x_1&=v_1\,\Delta t_1\\&=10\times 4=40\,{\rm m}\\ \\ \Delta x_2&=v_2\,\Delta t_2\\&=30\times 2=60\,{\rm m}\\ \\ \Delta x_3&=v_3\,\Delta t_3\\&=25\times 4=100\,{\rm m}\end{align*}Now use the definition of average velocity, $\bar{v}=\frac{\Delta x_{tot}}{\Delta t_{tot}}$, to find it over the whole path\begin{align*}\bar{v}&=\frac{\Delta x_{tot}}{\Delta t_{tot}}\\ \\&=\frac{\Delta x_1+\Delta x_2+\Delta x_3}{\Delta t_1+\Delta t_2+\Delta t_3}\\ \\&=\frac{40+60+100}{4+2+4}\\ \\ &=\boxed{20\,{\rm m/s}}\end{align*}
Problem (17): An object moving along a straight-line path. It travels with an average velocity $2\,{\rm m/s}$ for $20\,{\rm s}$ and $12\,{\rm m/s}$ for $t$ seconds. If the total average velocity across the whole path is $10\,{\rm m/s}$, then find the unknown time $t$.
Solution: In this velocity problem, the whole path $\Delta x$ is divided into two parts $\Delta x_1$ and $\Delta x_2$ with different average velocities and times elapsed, so the total average velocity across the whole path is obtained as \begin{align*}\bar{v}&=\frac{\Delta x}{\Delta t}\\\\&=\frac{\Delta x_1+\Delta x_2}{\Delta t_1+\Delta t_2}\\\\&=\frac{\bar{v}_1\,t_1+\bar{v}_2\,t_2}{t_1+t_2}\\\\10&=\frac{2\times 20+12\times t}{20+t}\\\Rightarrow t&=80\,{\rm s}\end{align*}
Note: whenever a moving object, covers distances $x_1,x_2,x_3,\cdots$ in $t_1,t_2,t_3,\cdots$ with constant or average velocities $v_1,v_2,v_3,\cdots$ along a straight-line without changing its direction, then its total average velocity across the whole path is obtained by one of the following formulas
- Distances and times are known:\[\bar{v}=\frac{x_1+x_2+x_3+\cdots}{t_1+t_2+t_3+\cdots}\]
- Velocities and times are known: \[\bar{v}=\frac{v_1\,t_1+v_2\,t_2+v_3\,t_3+\cdots}{t_1+t_2+t_3+\cdots}\]
- Distances and velocities are known:\[\bar{v}=\frac{x_1+x_2+x_3+\cdots}{\frac{x_1}{v_1}+\frac{x_2}{v_2}+\frac{x_3}{v_3}+\cdots}\]
Problem (18): A car travels one-fourth of its path with a constant velocity of $10\,{\rm m/s}$, and the remaining with a constant velocity of $v_2$. If the total average velocity across the whole path is $16\,{\rm m/s}$, then find the $v_2$?
Solution: This is the third case of the preceding note. Let the length of the path be $L$ so \begin{align*}\bar{v}&=\frac{x_1+x_2}{\frac{x_1}{v_1}+\frac{x_2}{v_2}}\\\\16&=\frac{\frac 14\,L+\frac 34\,L}{\frac{\frac 14\,L}{10}+\frac{\frac 34\,L}{v_2}}\\\\\Rightarrow v_2&=20\,{\rm m/s}\end{align*}
Problem (19): An object moves along a straight-line path. It travels for $t_1$ seconds with an average velocity $50\,{\rm m/s}$ and $t_2$ seconds with a constant velocity of $25\,{\rm m/s}$. If the total average velocity across the whole path is $30\,{\rm m/s}$, then find the ratio $\frac{t_2}{t_1}$?
Solution: the velocities and times are known, so we have \begin{align*}\bar{v}&=\frac{v_1\,t_1+v_2\,t_2}{t_1+t_2}\\\\30&=\frac{50\,t_1+25\,t_2}{t_1+t_2}\\\\ \Rightarrow \frac{t_2}{t_1}&=4\end{align*}
Read more related articles:
Kinematics Equations: Problems and Solutions
In the following section, some sample AP Physics 1 problems on acceleration are provided.
Problem (20): An object moves with constant acceleration along a straight line. If its velocity at instant of $t_1 = 3\,{\rm s}$ is $10\,{\rm m/s}$ and at the moment of $t_2 = 8\,{\rm s}$ is $20\,{\rm m/s}$, then what is its initial speed?
Solution: Let the initial speed at time $t=0$ be $v_0$. Now apply average acceleration definition in the time intervals $[t_0,t_1]$ and $[t_0,t_2]$ and equate them.\begin{align*}\text{average acceleration}\ \bar{a}&=\frac{\Delta v}{\Delta t}\\\\\frac{v_1 - v_0}{t_1-t_0}&=\frac{v_2-v_0}{t_2-t_0}\\\\ \frac{10-v_0}{3-0}&=\frac{20-v_0}{8-0}\\\\ \Rightarrow v_0 &=4\,{\rm m/s}\end{align*} In the above, $v_1$ and $v_2$ are the velocities at moments $t_1$ and $t_2$, respectively.
Problem (21): For $10\,{\rm s}$, the velocity of a car that travels with a constant acceleration, changes from $10\,{\rm m/s}$ to $30\,{\rm m/s}$. How far does the car travel?
Solution: Known: $\Delta t=10\,{\rm s}$, $v_1=10\,{\rm m/s}$ and $v_2=30\,{\rm m/s}$.
Method (I) Without computing the acceleration: Recall that in the case of constant acceleration, we have the following kinematic equations for average velocity and displacement:\begin{align*}\text{average velocity}:\,\bar{v}&=\frac{v_1+v_2}{2}\\\text{displacement}:\,\Delta x&=\frac{v_1+v_2}{2}\times \Delta t\\\end{align*}where $v_1$ and $v_2$ are the velocities in a given time interval. Now we have \begin{align*} \Delta x&=\frac{v_1+v_2}{2}\\&=\frac{10+30}{2}\times 10\\&=200\,{\rm m}\end{align*}
Method (II) with computing acceleration: Using the definition of average acceleration, first determine it as below \begin{align*}\bar{a}&=\frac{\Delta v}{\Delta t}\\\\&=\frac{30-10}{10}\\\\&=2\,{\rm m/s^2}\end{align*} Since the velocities at the initial and final points of the problem are given so use the below time-independent kinematic equation to find the required displacement \begin{align*} v_2^{2}-v_1^{2}&=2\,a\Delta x\\\\ (30)^{2}-(10)^{2}&=2(2)\,\Delta x\\\\ \Rightarrow \Delta x&=\boxed{200\,{\rm m}}\end{align*}
Problem (22): A car travels along a straight line with uniform acceleration. If its velocity at the instant of $t_1=2\,{\rm s}$ is $36\,{\rm km/s}$ and at the moment $t_2=6\,{\rm s}$ is $72\,{\rm km/h}$, then find its initial velocity (at $t_0=0$)?
Solution: Use the equality of definition of average acceleration $a=\frac{v_f-v_i}{t_f-t_i}$ in the time intervals $[t_0,t_1]$ and $[t_0,t_2]$ to find the initial velocity as below \begin{align*}\frac{v_2-v_0}{t_2-t_0}&=\frac{v_1-v_0}{t_1-t_0}\\\\ \frac{20-v_0}{6-0}&=\frac{10-v_0}{2-0}\\\\ \Rightarrow v_0&=\boxed{5\,{\rm m/s}}\end{align*}
Summary:
All these kinematic problems on speed, velocity, and acceleration are easily solved by choosing an appropriate kinematic equation. Keep in mind that these motion problems in one dimension are of the uniform or constant acceleration type. Projectiles are also another type of motion in two dimensions with constant acceleration.
Author: Dr. Ali Nemati
Date Published: 9/6/2020
Updated: Jun 28, 2023
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
