Average Velocity and Speed: Definition and Solved Examples

In physics, we usually need to know at what rate the particle moves.

To answer this question, we define two important kinematics variables; average velocity, and average speed.

Average Velocity and Speed Definition:

Average speed is the total distance traveled divided by the total time taken \begin{align*} Average\ speed&=\frac{\text{distance traveled}}{\text{elapsed time}}\\&=\frac{D}{\Delta t}\end{align*}
but average velocity is defined as the total displacement divided by the total time elapsed
\[Average\ velocity=\frac{\text{displacement}}{\text{elapsed time}}\]

Difference between average velocity and average speed:

• Average speed is a scalar quantity that depends on distance traveled but average velocity is a vector in physics that depends on total displacement and its direction is determined by the total displacement vector.
• Average speed is always positive (since total distance and total time are both always positive) but average velocity could be positive or negative which sign indicates the direction of the motion of the moving object. 
• In a straight-line motion without changing direction, average speed and average velocity are equal.
• If an object changes its direction, then the average speed is greater than the magnitude of the average velocity. 

Average velocity is a more useful quantity than the other since it describes both how fast and in what direction the objects move. Therefore, in one direction, say along the $x$ axis, the average velocity is defined and denoted by the following formula
\[\bar{v}=\frac{\Delta x}{\Delta t}\] The SI unit of velocity is meters per second ($\rm m/s$).

Other common units are Kilometers per second ($\rm Km/h$), feet per second ($\rm ft/s$), and miles per hour ($\rm mi/h$).

The dimension of velocity is also $L/T$. 

---

Examples of average velocity and speed:

Example (1): A bird is flying $100\,{\rm m}$ due east at $10\,{\rm m/s}$ and then it turns around and flies west in $15\,{\rm s}$ at $20\,{\rm m/s}$. Find the average velocity and average speed during the overall time interval.

Solution: First we must find the overall time. The first and second parts are done in $\Delta t_1=\frac{\Delta x}{v}=\frac{100}{10}=10\,{\rm s}$ and $\Delta t_2=15\, {\rm s}$. Thus the overall time of flying of the bird is $\Delta t_{tot}=10+15=25\,{\rm s}$.

The distance traveled by the bird due west is $d_w=v\Delta t_2=20 \times 15=300\,{\rm m}$. Therefore, by definition of the average speed, we have
\[\text{Average speed}=\frac{(100+300)\,{\rm m}}{25\,{\rm s}}=16\ {\rm \frac ms}\] As we can see from the figure, the displacement vector is $\Delta x=x_f-x_i=-200-0=-200\,{\rm m}$. So the average velocity is found as \[\bar{v}=\frac{\Delta x}{\Delta t}=\frac{-200\,{\rm m}}{25\,{\rm s}}=-8\ {\rm m/s}\]The negative indicates that the average velocity is towards the $-x$ direction.

---

 

Example (2): An object travels $1200$ m in 30 s, what is its average velocity?

Solution: applying the average velocity definition, we get \begin{align*} \bar{v}&=\frac{\Delta x}{\Delta t}\\\\&=\frac {1200\,{\rm m}}{30\,{\rm s}}\\\\&=40\,{\rm m/s}\end{align*}

---

 

Example (3): An object travels 1000 m with an average velocity of 50 m/s, what is the total time of travel?

Solution: in the definition of average velocity, solving for $t$ we get \begin{align*} \Delta t&=\frac {\Delta x}{\bar{v}}\\\\&=\frac {1000\,{\rm m}}{50\,{\rm s}}\\\\&=20\,{\rm s}\end{align*}

---

Graphical Interpretation of Velocity:

To show the motion of a particle, usually a position–versus-time graph (or simply position graph) is used.

In such plots, every point in the plane represents the position and the corresponding time of a moving object. 

If you know the velocity of an object at any instant of time and plot them against the overall time interval, we arrive at a velocity-time graph.

The curves in the $x-t$ graph are not the path of the motion. As you can see later, the straight-line movement of a car does not yield a straight line!.

Further, time is specified on the horizontal axis. Using these graphs one can extract (or simplify) more information about the type of motion. Let's consider the velocity of a moving particle to be constant during any successive equal-time intervals, then its $x-t$ graph is a straight line. This type of motion is called uniform motion. 

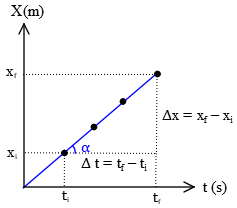
In this case, the average velocity is the slope of the position-versus-time graph. In one-dimensional motion, this is simply \[\bar{v}=\frac{\Delta x}{\Delta t}={\rm slope\ of\ the\ x-t\ graph}\] Therefore, from the mathematical viewpoint, in the uniform motion, equal displacements occur during any successive equal-time intervals.

If the velocity is not constant, the motion's graph is a curve as shown in the figure below (the actual path of the motion could be a straight line, this is a reason why the position graph is not a picture of the path!).

In such a case, the object's average velocity during each particular time interval is the slope of the $x-t$ graph that connects the initial and final points in that interval $\Delta t$.

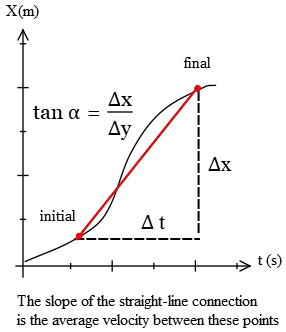
In mathematics, the slope of the line connecting two points $A$ and $B$, in a plane, defines as $\tan$ of a smaller angle with the $x$ axis. Therefore, we can relate the average speed or velocity (in which those two points get closer together) to the $\tan$ of a smaller angle as \[\text{average speed}=\text{slope of the line $AB$}=\tan \alpha\]

---

 

Example (4): An student arrives at her school, and first walks $900\,{\rm m}$ to the north then $300\,{\rm m}$ toward the east. Finally walks $500\,{\rm m}$ along the south. The total time of walking is $5$ minutes. 
(a) Find the distance traveled by her?
(b) Find the average velocity.

Solution:
(a) To find the total distance traveled, one should add the lengths of each part of the path with each other. So \begin{align*} \text{distance}&=AB+BC+CD\\&=900+300+500\\&=1700\,{\rm m} \end{align*}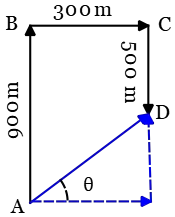
(b) As mentioned, average velocity is a vector quantity that depends on the total displacement of an object between initial and final points. Thus, draw a vector that connects those points to each other as the figure below \begin{align*} \text{displacement}\,:\, \overrightarrow{AD} &=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}\\\\|\overrightarrow{AD}|&=\sqrt{(300)^2 +(400)^2 }\\\\&=500\,{\rm m}\end{align*}
In the first line, the definition of displacement as a vector addition was represented, and using the Pythagorean theorem its magnitude was computed. Now, by definition of average velocity, its magnitude is \begin{align*}|\bar{v}|&=\frac{\text{displacement}}{\text{total time}}\\\\&=\frac{500\,{\rm m}}{5 \times 60\,{\rm s}}\\\\&=\frac {5}{3}\,{\rm \frac m s} \end{align*} We can go further and find its direction. Recall that the average velocity is a vector in the same direction as the displacement vector. Therefore,\begin{align*}\theta &=\tan^{-1} \left(\frac{\text{y-component of $\overrightarrow{AD}$}}{\text{x-component of $\overrightarrow{AD}$}} \right)\\\\&=\tan^{-1} \left(\frac{400}{300}\right)\\\\&\approx \,53^{\circ} \end{align*} 
Note: in everyday language, we usually define velocity as the distance traveled divided by the elapsed time, say here $v=\frac{1700}{5\times 60}=\frac{17}{3}\,{\rm m/s}$ but as you can see, velocity definition in physics is different because velocity is defined as a vector quantity. 

---

 

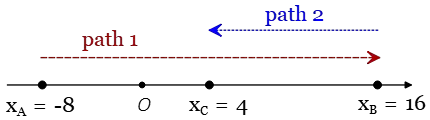
Example (5): A car moves along the $x$ axis as the following figure. Its position at instant $t_1=2\,{\rm s}$ is at $A$. It is positioned at $B$ at time $t_2=5\,{\rm s}$ then returns and passes through the point $C$ at $t_3=10\,{\rm s}$. 
(a) What are the average speed and velocity of the car between the times $t_1$ and $t_2$?
(b) Now find the above quantities in the time interval $t_1$ and $t_3$.

Solution:
(a) We denote the position of the car at any moment of time as $x_i(t)$ where subscript $i$ labels the location of the car. The distance ($D$) and magnitude of displacement ($\Delta x$) in interval $t_1$ and $t_2$ are \begin{align*} D &= x_B(t_B)-x_A(t_A) \\ &= 16-(-8) \\ &=24\,{\rm m}\\\\ \Delta x &= x_B(t_B)-x_A(t_A) \\ &= 16-(-8) \\&=24\,{\rm m}\end{align*}

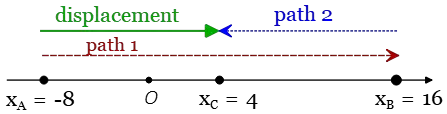
Since in the interval $t_1$ and $t_2$ the object moving along a straight-line and the direction of the movement is constant so distance $=\Delta x=24\,{\rm m}$. The average speed and average velocity $\bar{v}$ are also the same \begin{align*}\text{average speed}&=\bar{v}\\ &=\frac{\text{distance or displacement}}{\text{time interval}}\\\\&=\frac{24}{5-2}=8\,{\rm m/s} \end{align*}
b) If one connects the initial and final positions, the displacement vector $\Delta x$ is obtained which, in a subsequent step, dividing by $\Delta t=t_C-t_A$ get the average velocity $\bar{v}$.
\begin{align*}\Delta x_{AC}&=x_C-x_A\\&=4-(-8)=12\,{\rm m}\\\\ \therefore\, \bar{v} &=\frac{\Delta x_{AC}}{\Delta t}\\\\&=\frac{12}{10-2}=\frac{3}{2}\,{\rm \frac ms }\end{align*}But since in interval $t_1$ to $t_3$, the motion has a turning point $B$ (where the velocity of a moving object gets zero and reverse its direction) so distance is not equal with the magnitude of displacement.\begin{align*}\text{distance}&=|(x_B-x_A)|+|(x_C-x_B)|\\\\&=\left|16-(-8)\right|+\left|4-16\right|\\\\&=36\,{\rm m}\\\\ \text{average speed}&=\frac{\text{total distance}}{\text{total time}}\\\\&= \frac{36}{10-2}=4.5\,{\rm \frac m s}\end{align*} Recall that distance is a scalar quantity in physics so we should pick out its absolute value. 

Instantaneous Velocity Definition:

The average velocity is not a useful quantity for analyzing non-uniform motions.

Very often it is necessary to know the object's velocity at an instant in time. In this case, the 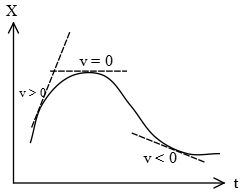instantaneous velocity can be defined. 

Instantaneous velocity or simply velocity is the limit of average velocity $\bar{v}=\frac{\Delta x}{\Delta t}$ as $\Delta t$ approaches zero.

In the language of calculus, this limit is called the derivative of $x$ with respect to $t$ and is written as $\frac{dx}{dt}$. Thus in the mathematical form, we can state \[v_x=\lim_{\Delta t \to 0}\frac{\Delta x}{\Delta t}=\frac{dx}{dt}\] Therefore, the instantaneous velocity at time $t$ is the slope of the line that is tangent to the position-versus-time graph at the instance $t$. The time interval $\Delta t$ is always positive, so $v_x$ has the same sign as $\Delta x$.

Solved Examples of Velocity: 

Example (1): An object travels at 10 m/s for 20 s, how far has it traveled?

Solution: The known quantities are: instantaneous velocity and time taken, so using the definition of velocity, we have \begin{align*} \Delta x &=\bar{v}\Delta t\\&={10\,{\rm \frac ms}}\times{20\,{\rm s}}\\&=200\,{\rm m}\end{align*}

Example (2): The position of a particle varies with time according to the equation $x=40-5t-5t^2$ where $x$ and $t$ are in $\rm m$ and $\rm s$, respectively. Find 
(a) The particle's average velocity between $t=1\,{\rm s}$ and $t=2\,{\rm s}$. 
(b) The instantaneous velocity at $t=2\,{\rm s}$.

Solution:
(a) By definition of the average velocity, we must first find the displacement during that interval\begin{align*}x(t=2\,{\rm s})&=40-5(2)-5(2)^2=10\ {\rm m}\\x(t=1\,{\rm s})&=40-5(1)-5(1)^2=30\ {\rm m}\\ \Delta x&=x(t=2\,{\rm s})-x(t=1\,{\rm s})\\&=10-30=-20\ {\rm m}\end{align*} Therefore, the average velocity becomes    \[\bar{v}=\frac{\Delta x}{\Delta t}=\frac{-20}{(2-1)}=-20\ {\rm m/s}\] The negative shows the direction of the velocity vector which is towards the negative $x$ axis.
(b) The instantaneous velocity is defined as the derivative of position with respect to time $v_x=\frac{dx}{dt}$ \begin{align*}v_x&=\frac{dx}{dt}\\&=\frac{d}{dt} (40-5t-5t^2)\\&=(-5-10\,t)\ {\rm \frac ms}\end{align*} Evaluating the velocity at $t=2\,{\rm s}$ gives \[v_x (t=2\,{\rm s})=-5-10(2)=-25\ {\rm m/s}\] In both cases, the negatives indicate the particle moves in the $-x$ direction. 

---

To master this topic, you should practice more problems on speed, velocity, and acceleration. Here we only presented a brief introduction with some examples.