- Home
- Physics Problems
- Problems
Solved Problems
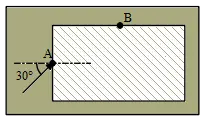
The drawing shows a rectangular block of glass (n=1.52) surrounded by liquid carbon disulfide (n=1.63). A ray of light is incident on the glass at point A with a $30^\circ $ angle of incidence.
At what angle of refraction does the ray leave the glass at point B?
Snell's law: describes how light bends when traveling from one medium to the 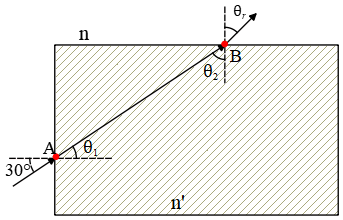 next. i.e. it states that $n_1\,{\sin {\theta }_1\ }=n_2\,{\sin {\theta }_2\ }$ , where $\theta $'s represents the angles the light makes with the normal in the mediums and $n$ is the refractive index of the object or medium.
next. i.e. it states that $n_1\,{\sin {\theta }_1\ }=n_2\,{\sin {\theta }_2\ }$ , where $\theta $'s represents the angles the light makes with the normal in the mediums and $n$ is the refractive index of the object or medium.
Now first use the Snell's law and find the refracted angle ${\theta }_1$ from the left side
\begin{align*} n\,{\sin {\theta }_i\ }&=n^{'}\,{\sin {\theta }_1\ } \\ 1.63\,{\sin 30{}^\circ \ }&=1.52\,{\sin {\theta }_1\ } \\ \to {\theta }_1&=32.42{}^\circ \end{align*}
From the geometry and the drawing above, we have \[{\theta }_1+{\theta }_2=90\Rightarrow \ {\theta }_2=90-32.42=57.58{}^\circ\]
By applying the Snell's law again at point B, we obtain
\begin{align*} n^{'}\,{\sin {\theta }_2\ }&=n\,{\sin {\theta }_r\ } \\ \to {\theta }_r&={{\sin}^{-1} \left(\frac{n^{'}}{n}{\sin {\theta }_2\ }\right)\ }\\ &=51.92\end{align*}
You are trying to photograph a bird sitting on a tree branch, but a tall hedge is blocking 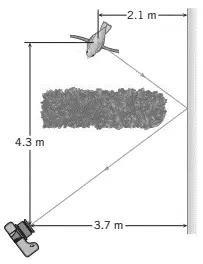 your view. However, as the drawing shows, a plane mirror reflects light from the bird into your camera. For what distance must you set the focus of the camera lens in order to snap a sharp picture of the bird's image.
your view. However, as the drawing shows, a plane mirror reflects light from the bird into your camera. For what distance must you set the focus of the camera lens in order to snap a sharp picture of the bird's image.
Solution 1: In plane mirrors, the angle of incidence ${\theta }_i$ equals the angle of reflection ${\theta }_r$ i.e. ${\theta }_i={\theta }_r$.
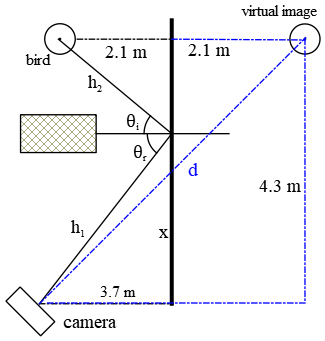
In order to get a sharp picture we must determine $h_1+h_2$ i.e. the direct distance of image from camera. As drawing shows
\[{\tan {\theta }_r\ }=\frac{x}{3.7}={\tan {\theta }_i\ }=\frac{4.3-x}{2.1}\ \ \ \Rightarrow \ \ x=\frac{3.7}{2.1}\left(4.3-x\right)=2.74\mathrm{m}\]
using the Pythagorean theorem, we can obtain the values of $h_1$ and $h_2$
\begin{gather*} h_1=\sqrt{x^2+{\left(3.7\right)}^2}=4.60 \\ h_2=\sqrt{{\left(4.3-x\right)}^2+{\left(2.1\right)}^2}=2.61 \\ \therefore\ h_1+h_2=7.21\ \mathrm{m}\end{gather*}
Solution 2: plane mirrors forms a virtual image! Therefore, camera sees a virtual image and the blue triangle in the drawing shows this image (using the Pythagorean Theorem)
\[d=\sqrt{{\left(3.7+2.1\right)}^2+{\left(4.3\right)}^2}=7.21\ \mathrm{m}\]
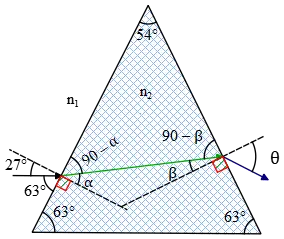
The drawing shows a horizontal beam of light that is incident on a prism made 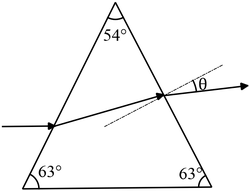 from ice. The base of the prism is also horizontal. The prism ($n=1.31$) is surrounded by oil whose index of refraction is $1.51$. Determine the angle $\theta $ that the exiting light makes with the normal to the right face of the prism.
from ice. The base of the prism is also horizontal. The prism ($n=1.31$) is surrounded by oil whose index of refraction is $1.51$. Determine the angle $\theta $ that the exiting light makes with the normal to the right face of the prism.
Use the ray diagram in the below and apply the Snell's law to determine $\theta $:
\[n_1\,{\sin 27{}^\circ \ }=n_2\,{\sin \alpha \ }\to \alpha ={{\sin}^{-1} \left(\frac{n_1}{n_2}{\sin 27{}^\circ \ }\right)\ }=31.55{}^\circ \]
From the geometry we have (the sum of the internal angles of a triangle is $180{}^\circ $):
\[\left(90-\alpha \right)+54+\left(90-\beta \right)=180{}^\circ \to \ \alpha +\beta =54\ \Longrightarrow \beta =22.45{}^\circ \]
\[n_2\,{\sin \beta \ }=n_1\,{\sin \theta \ }\to \theta ={{\sin}^{-1} \left(\frac{n_2}{n_1}{\sin \beta \ }\right)\ }=19.34{}^\circ \]
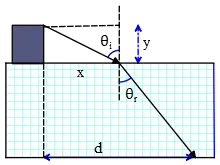
A spotlight on a boat is $y=2.7\,\mathrm{m}$ above the water ($n=1.33$), and 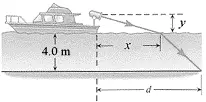 the light strike the water at a point that is $x=9.4\, \mathrm{m}$ horizontally displaced from the spotlight (see the drawing). The depth of the water is $4.0\, \mathrm{m}$. Determine the distance $d$, which locates the point where the light strikes the bottom from the boat.
the light strike the water at a point that is $x=9.4\, \mathrm{m}$ horizontally displaced from the spotlight (see the drawing). The depth of the water is $4.0\, \mathrm{m}$. Determine the distance $d$, which locates the point where the light strikes the bottom from the boat.
This is just a simple combination of geometry and Snell's law:
\[n\,{\sin {\theta }_i\ }=n_w\,{\sin {\theta }_r\ }\] \[\Rightarrow {\theta }_r={{\sin}^{-1} \left(\frac{n}{n_w}{\sin {\theta }_i\ }\right)\ }={{\sin}^{-1} \left(\frac{1}{1.33}\frac{9.4}{\sqrt{{9.4}^2+{2.7}^2}}\right)\ }=46.27{}^\circ \] using the definition of the Tangent of an angle in a right angled triangle, we can find the desired distance $d$ as follows:
\[{\tan {\theta }_r\ }=\frac{d-x}{4}\ \ \Rightarrow \ \ d=4\times {\tan 46.27{}^\circ \ }+x=4.18+9.4=13.58\ \mathrm{m}\]
A point source of light is submerged 2.2 m below the surface of a lake (n=1.33) and emits rays in all directions. On the surface of the lake, directly above the source, the area illuminated is a circle. What is the maximum area that this circle could have?
All the rays emitted from the point source, are refracted at various angles. If 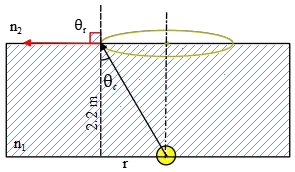 the incident angle ${\theta }_i$ is such that the refracted angle becomes $90{}^\circ $, then all of the energy of the ray transmitted parallel to the surface. This incident angle ${\theta }_c$ is called the critical angle.
the incident angle ${\theta }_i$ is such that the refracted angle becomes $90{}^\circ $, then all of the energy of the ray transmitted parallel to the surface. This incident angle ${\theta }_c$ is called the critical angle.
All the rays with an incident angle greater than ${\theta }_c$, will be reflected back into the medium from which they came (total reflection).
Therefore, we must find the critical angle and then from its geometry find the maximum area that forms.
\[{\sin {\theta }_c\ }=\frac{n_1}{n_2}=\frac{1}{1.33}\to {\theta }_c=48.75{}^\circ \]
\[{\tan {\theta }_c\ }=\frac{r}{2.2}\to r=2.2\,{\tan 48.75{}^\circ \ }=2.50\,\mathrm{m}\]
\[Area=\pi r^2=\pi {\left(2.50\right)}^2=19.77\ {\mathrm{m}}^{\mathrm{2}}\]
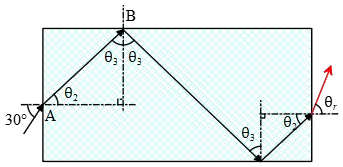
The drawing shows a rectangular block of glass (n=1.52) surrounded by liquid 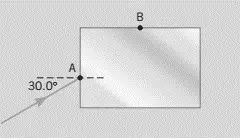 carbon disulfide (n=1.30). A ray of light is incident on the glass at point A with an angle of incidence of $30{}^\circ $.
carbon disulfide (n=1.30). A ray of light is incident on the glass at point A with an angle of incidence of $30{}^\circ $.
At what angle of refraction does the ray leave the glass at point B?
Let $n_1=1.30$ and $n_2=1.51$
Use Snell's law to find the refracted light at point A \[n_1\,{\sin 30{}^\circ \ }=n_2\,{\sin {\theta }_2\ }\to {\theta }_2=25.5{}^\circ \]
From the geometry, we have: \[{\theta }_2+{\theta }_3=90\to {\theta }_3=90-25.5=64.5{}^\circ \]
Now because the light passes from a higher refractive index ($n_2$) into a medium with a lower refractive index ($n_1$) we must first determine the critical angle.
If the incident angle is greater than ${\theta }_c$, then total internal reflection occurs.
The critical angle is found by the following formula: \[{\sin {\theta }_c\ }=\frac{n_1}{n_2}=\frac{1.30}{1.51}\to {\theta }_c=59.42{}^\circ \]
Because ${\theta }_3>{\theta }_c$ so total internal reflection occurs.
Light leaves B at angle ${\theta }_3$ and as shown in the figure, after occurring total internal reflection once again at the bottom side, the light ray leaves the block at angle ${\theta }_R$.
Therefore, use again the Snell's law at right side
\begin{align*} n_2\,{\sin {\theta }_2\ }&=n_1\,{\sin {\theta }_R\ }\\ \\ \to {\theta }_R&={{\sin}^{-1} \left(\frac{n_2}{n_1}{\sin {\theta }_2\ }\right)\ }\\ \\&={{\sin}^{-1} \left(\frac{1.51}{1.30}{\sin 25.5{}^\circ \ }\right)\ }\\ \\&=30{}^\circ \end{align*}
A narrow beam of ultrasonic waves reflects off a liver tumor as shown. If the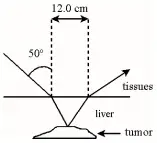 speed of the wave is $20\%$ less in the liver than in the surrounding tissues, determine the depth of the tumor.
speed of the wave is $20\%$ less in the liver than in the surrounding tissues, determine the depth of the tumor.
Note: the refractive index defines as 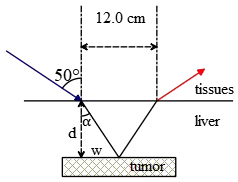
\[n=\frac{c}{v}\]
Where $c$ is the speed of light in the vacuum (which is constant) and $v$ is the velocity of light (or other waves) in the medium. So
From Snell's law:
\begin{align*} n_{tiss}\,{\sin 50\ }&=n_{liv}\,{\sin \alpha \ } \\ \\ \to \alpha &={{\sin}^{-1} \left(\frac{n_{tiss}}{n_{liv}}{\sin 50{}^\circ \ }\right)\ }\end{align*}
Since the refractive index of the mediums are not given so use the definition of the refractive index to find the ratio of the refractive index of the mediums in terms of velocities as follows
\[\frac{n_{tiss}}{n_{liv}}=\frac{v_{liv}}{v_{tiss}}=0.8\]
Now substitute it into $\alpha $
\[\alpha ={{\sin}^{-1} \left(0.8{\sin 50{}^\circ \ }\right)\ }=37.79{}^\circ \]
From the law of reflection, $w=\frac{12}{2}=6\ \mathrm{cm}$
\[\therefore {\tan \alpha \ }=\frac{w}{d}\ \Longrightarrow d=\frac{6}{{\tan 37.79{}^\circ \ }}=7.73\ \mathrm{cm}\]
A ray of light impinges from air onto a block of ice ($n=1.309$) at a $70{}^\circ $ angle of incidence. Assuming that this angle remains the same, find the difference ${\theta }_{2,ice}-{\theta }_{2,water}$ in the angles of refraction when the ice turns to water ($n=1.333$)
Use Snell's law to find the refracted ray in the second medium: \[n_1\,{\sin {\theta }_1\ }=n_2\,{\sin {\theta }_2\ }\to {\theta }_2={{\sin}^{-1} \left(\frac{n_1}{n_2}{\sin {\theta }_1\ }\right)\ }\mathrm{but}\ n_1=1\ \] Now substitute the values of the ice and water into the above relation and then subtract them from each other \begin{align*} \Rightarrow {\theta }_{2,ice}-{\theta }_{2,water} &={{\sin}^{-1} \left(\frac{{\sin {\theta }_1\ }}{n_{ice}}\right)-\ }{{\sin}^{-1} \left(\frac{{\sin {\theta }_1\ }}{n_{water}}\right)\ }\\ & ={{\sin}^{-1} \left(70{}^\circ \frac{1}{1.309}\right)\ }-{{\sin}^{-1} \left(70{}^\circ \frac{1}{1.333}\right)\ }=1.054{}^\circ \end{align*}
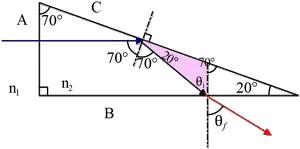
A horizontal beam of light is incident on face A of the prism ($n_2\ =\ 1.48$), 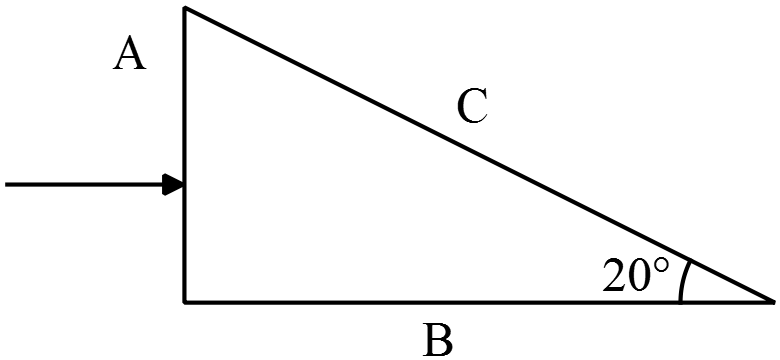 which is surrounded by water ($n_1 = 1.33$), as shown in the drawing. Find the angle that the beam emerges from the prism with respect to the normal.
which is surrounded by water ($n_1 = 1.33$), as shown in the drawing. Find the angle that the beam emerges from the prism with respect to the normal.
Light is incident at angle $70{}^\circ$ on the face $C$. Because light moves through a denser medium into a less dens one, then we must first determine the critical angle $\theta_{cri}$ as below \[{\sin {\theta }_{cri}\ }=\frac{n_1}{n_2}\to {\theta }_{cri}={{\sin}^{-1} \left(\frac{1.33}{1.48}\right)\ }\sim \ 64{}^\circ \] Since ${\theta }_{rc}>{\theta }_{cri}$ therefore total internal reflection can occur.
From the geometry (colored triangle), we can find the incident angle ${\theta }_i=50{}^\circ $ on the face $B$ and then using the Snell's law we obtain the refracted ray on face $B$
\[n_2\,{\sin {\theta }_i\ }=n_1\,{\sin {\theta }_f\ }\Rightarrow {\theta }_f={{\sin}^{-1} \left(\frac{n_2}{n_1}{\sin 50^\circ \ }\right)\ }=58.5^\circ \]
Note: the sum of the internal angles of a triangle is always $180^\circ $.
A piece of ice is cut into a square block as shown. Its index of refraction is 1.3. Light is incident on the top surface from the right as shown. What incident angle ${\theta }_c$ would lead to total internal reflection in the ice block, so no light would escape to the left?
Recall that two conditions are required to occur total internal reflection: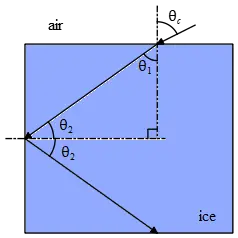
(a) The light propagating from a more dense medium into a less dense medium.
(b) The angle of incidence is greater than the critical angle.
Use Snell's law formula to find the ${\theta }_c$
\[n_a\,{\sin {\theta }_c\ }=n_i\,{\sin {\theta }_1\ }\Rightarrow (1.3)\,{\sin {\theta }_1\ }=1\,{\sin {\theta }_c\ }\]
Now calculate the critical angle for the ice-air boundary as \begin{align*}n_i\,{\sin {\theta }_{cri}\ }&=n_a\,{\sin 90{}^\circ \ }\\ \\ \Rightarrow {\sin {\theta }_{cri}\ }&=\frac{1}{1.3} \\ \\\Rightarrow {\theta }_{cri}\ \sim \ 50.28{}^\circ \end{align*} (For critical angle, the angle of refraction is $90{}^\circ $).
Therefore, if ${\theta }_2>{\theta }_{cri}$ then the total internal reflection occurs on the left side.
By supposing ${\theta }_2={\theta }_{cri}$ and using the figure, we have
\[{\theta }_1+{\theta }_2=90{}^\circ \Rightarrow {\theta }_1=90-50.28\ \sim \ 39.72{}^\circ \]
By substitute it into the following relation, we obtain the minimum angle that the total internal reflection can occur.
\begin{align*} (1.3)\,{\sin {\theta }_1\ }&=1\,{\sin {\theta }_c\ } \\ \Rightarrow {\theta }_c&={{\sin}^{-1} ((1.3){\sin 39.72^\circ})\ }\sim \ 56.17^\circ \end{align*}
Therefore, if ${\theta }_c>56.17{}^\circ $, total internal reflection occurs.
A rectangular slab of glass has an index of refraction for red light ($\lambda =700\,{\rm nm}$) of $1.724$ and for blue light ($\lambda =450\,{\rm nm}$) of $1.770$. The angle of refraction for the blue beam inside the glass is $20.24^\circ $. What is the angle of refraction for the red beam?
First, use the Snell's law to find the incident angle as
\begin{align*} n_i\,{\sin {\theta }_i}&=n_b\,{\sin {\theta }_{rb}}\\ \\ \Rightarrow {\theta }_i&={{\sin}^{-1} \left(\frac{n_b}{n_i}{\sin {\theta }_{rb}\ }\right)\ }\\ \\ &={{\sin}^{-1} \left(\frac{1.770}{1}{\sin 20.24{}^\circ \ }\right)\ }\\ \\&=37.75{}^\circ \end{align*} Now using Snell's law once again, calculate the reflected angle for red beam as \begin{align*} n_i\,{\sin {\theta }_i\ }&=n_r\,{\sin {\theta }_{rr}\ } \\ \\ \Rightarrow {\theta }_{rr}&={{\sin}^{-1} \left(\frac{n_i}{n_r}{\sin {\theta }_i\ }\right)\ }\\ \\ &={{\sin}^{-1} \left(\frac{1}{1.724}{\sin 37.75{}^\circ \ }\right)\ }\\ \\&=20.80{}^\circ \end{align*}
A deep-sea diver wearing a spherical plastic helmet of diameter 0.50 m looks directly at a fish, and the fish looks directly back. The fish is 2.00 m from the helmet, and the diver's eye is 0.20 m from the helmet. Ignore any refraction effects from the plastic helmet itself. The index of refraction of the water is 1.33.
(a) How far does the fish appear to be from the surface of the helmet as observed by the diver?
(b) How far does the diver's eye appear to be from the surface of the helmet as observed by the fish?
(a) In optics, images can form by reflection from a spherical mirrors or refraction by a refracting surface (thin lenses,$\dots$). For reflection from a spherical mirror with focal length $f$, the image $q$ and object $p$ distances are related together by the following relation
\[\frac{1}{p}+\frac{1}{q}=\frac{1}{f}\]
But the image and object distances from a spherical boundary of radius $R$ which is between the two transparent materials of indices of refraction $n_1$ and $n_2$ is given by the well-known equation below
\[\frac{n_1}{p}+\frac{n_2}{q}=\frac{n_2-n_1}{R}\]
The sketch of the problem is shown.
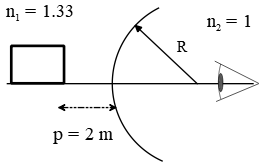
Using the above equation, we obtain
\begin{gather*} \frac{n_1}{p}+\frac{n_2}{q}=\frac{n_2-n_1}{+R} \\ \\ \frac{1.33}{2}+\frac{1}{q}=\frac{1-1.33}{0.5/2} \\ \\ \Rightarrow \frac{1}{q}=-\frac{0.33}{\frac{0.5}{2}}-\frac{1.33}{2}=1.985 \\ \\ \Rightarrow q=-0.503\quad {\rm m}\end{gather*}
The sign convention for refraction cases is the same as thin lenses. Since the center of curvature is on the refracted-light side of the surface so $R>0$.
The negative sign for $q$ indicates that the image is in front (incident-light side) of the helmet, in other words, it is in the same medium as the object.
Therefore, the image of the fish must be virtual and closer to the helmet than it actually is.
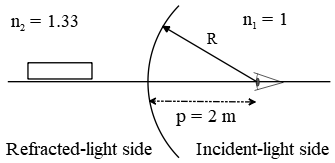
(b) In this case since the center of curvature is located in incident-light side of the refracting surface so $R<0$.
\begin{gather*} \frac{n_1}{p}+\frac{n_2}{q}=\frac{n_2-n_1}{-R} \\ \\ \frac{1}{0.2}+\frac{1.33}{q}=\frac{1.33-1}{-\left(\frac{0.5}{2}\right)} \\ \\ \Rightarrow q=-0.21\quad {\rm m}\end{gather*} The negative sign of $q$ means that the image of the diver's eye is on the same side of the object.
The relation $n_1{\,\sin {\theta }_1\ }=n_2{\,\sin {\theta }_2\ }$ which applies as a ray of light strikes an interface between two media, is known as:
(a) Gauss's law
(b) Snell's law
(c) Faraday's law
(d) Cole's law
(e) Law of sines
Snell's law describes the bending of a light ray as it passes from one medium to another. In the mathematical language is $n_1{\,\sin {\theta }_1\ }=n_2{\,\sin {\theta }_2\ }$ where n's are the refractive indices.
The correct answer is B.
The index of refraction of benzene is 1.80. The critical angle for total internal reflection, at a benzene-air interface, is about:
(a) $56^\circ $
(b) $47^\circ $
(c) $34^\circ $
(d) $22^\circ $
(e) $18^\circ $
When light passes from a medium of high index of refraction to a medium of lower index of refraction, a physical phenomenon called total internal reflection occurs. The critical angle $\theta_c$ at which this phenomenon occurs at the interface of the mediums is found as \[\sin \theta_c=\frac{n_2}{n_1}\quad ,\quad (n_1>n_2)\]
Benzene and air have indices of refraction $n_1=1.8\ ,\ n_2=1$, respectively. Thus the critical angle at which total internal reflection occurs when light travels from benzene to air is \begin{gather*} \sin \theta_c=\frac{n_2}{n_1}=\frac{1}{1.8} \\\\ \Rightarrow \quad \theta_c=33.7^\circ \end{gather*}
For more solved problems on the index of refractions refer, here.
Monochromatic light, at normal incidence, strikes a thin film in air. If $\lambda $ denotes the wavelength in the film, what is the thinnest film in which the reflected light will be a maximum?
(a) Much less than $\lambda $
(b) $\lambda /4$
(c) $\lambda /2$
(d) $3\lambda /4$
(e) $\lambda $
When a monochromatic light incident on a thin film of refractive index $n$ and thickness $t$, due to combination of the reflected rays from upper and lower surfaces of the film interference in the reflected rays can be occurred. In general, the condition for constructive interference in thin films is
\[2t=\left(m+\frac{1}{2}\right){\lambda }_n\ ,\ \ m=(0,1,2,\dots )\]
Where ${\lambda }_n$ is the wavelength of light in the film which is found by ${\lambda }_n=\lambda /n$. $\lambda $ is the wavelength in the vacuum.
Maximum pattern in the interference language means a constructive fringe. $m=0$ in the equation above, gives the thinnest film that is
\[t=\frac{\left(m+\frac{1}{2}\right){\lambda }_n}{2}=\frac{{\lambda }_n}{4}\]
The correct answer is B.
MOST USEFUL FORMULA IN REFRACTION:
Law of refraction (Snell's law):
\[n_1\sin \theta_i=n_2\sin \theta_r\]
where $n$s are the indexes of refraction of the materials.
$\theta_i$ and $\theta_r$ are the angles of incidence and refraction.
Total internal reflection:
when light travells from a medium with high refractive index to that with low refractive index this phenomena will occur. such as water to air.
Critical angle is the angle at which total internal reflection can be occured
\[\sin \theta_{cri}=\frac{n_b}{n_a} \quad , \quad n_a>n_b\]
If the angle of incidence $\theta_a$ in the dense medium is larger than or equal to $\theta_{cri}$ then total internal reflection will occur.
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
