Plane mirror- Definition, Properties and Ray Diagram

Mirrors are defined as one side-polished surface that can reflect the light rays.

Plane mirrors in physics are the ones that have a flat reflecting surface and produce always a virtual image.

In this tutorial, we review the most important topics in the plane (flat) mirrors in physics including image formation by ray diagrams, image properties of plane mirrors, proving the equality of image and object distance, and definition of lateral magnification in plane mirrors.

Image formation in the plane mirror by ray diagram :

Let's start to define some elements of the method of image formation by a plane mirror.

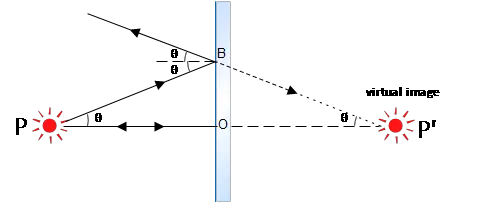
As shown in the figure all light rays emanating from a point source $P$ are reflected from a plane mirror so that the extensions of the reflected rays backward appear to come (or diverge) from point $P'$ (The rays do not actually pass through the mirror since the most mirrors in the market are opaque).

We call point $P$ an object point and point $P'$ the corresponding image point.

Virtual image in plane mirror
Now we're going to answer this question that why does a plane mirror create a virtual image?

By principle, in optics, an image is formed where reflected light rays actually intersect each other or where they appear to come from.

For flat mirrors, no light rays actually intersect at the point $P'$ (image point) but from the point of view of an observer appears that the light rays originate from that point and that's why we called this image a virtual image.

In other words, since the light rays don't intersect each other on a physical screen so proved that the image formed in a plane mirror is virtual. There are situations where reflected light rays actually meet each other such as a concave mirror.

By practicing a number of problems on the concave mirror, you can get a better understanding.

Another reason why the image is virtual in plane mirrors is that image is formed on the opposite side of the mirror where the object does not exist.

The above setup is based on one point source, to find the precise position of an image formed by a plane mirror, we must use at least two rays diverging from a point, say $P$, of an extended object, like an arrow in the figure. One of them incident normally on the mirror and the other strikes the mirror at an angle of incidence $\theta$ and is reflected at an equal angle with the normal (due to the law of reflection: all rays striking any surface (polished or rough) are reflected at an angle from the normal equal to the incident angle).

Extending those two reflected rays backward they intersect each other at point $P'$, at a distance $s'$, behind the plane mirror. The distance $s'$ which is the distance of the image from the plane mirror is called the image distance.

Now we geometrically prove another important question arising in plane mirrors using a ray diagram.

Why is the image distance and object distance equal in the plane mirror?

Answer: Suppose the two rays from the source point $P$ striking the mirror as shown in the figure, one of those rays follows the path $OP$ and the other follows the indirect path $PB$.

The backward extension of the ray $OP$ is along the horizontal axis. The $PB$ ray also reflects at an equal angle with the incident angle then extent backward it to meet the horizontal path. The intersection of the two backward rays lies along the horizontal axis, behind the mirror, where the image point $P'$ is formed. From this construction, one can observe that the two triangles $\Delta POB$ and $\Delta P'OB$ are similar since all angles between those are the same.

Recall from high school geometry that when two triangles are similar then there is a proportionality between their corresponding sides.

equality image and object distance geometry prove
Consequently, from similarity of triangles $\Delta POB$ and $\Delta P'OB$ we have the following ratios between the lengths of the triangles
\begin{align*}\frac {OP}{OP'}=\frac {OB}{OB} =1\\ \frac {PB}{P'B}=\frac {OB}{OB} =1 \end{align*}
From the first equality we can obtain the equality of distance object $OP$ with the image distance $OP'$ i.e. $OP=OP'$ which is the required result.

Now that the basics of image formation using a ray diagram in plane mirrors are reviewed, practice the following example.

Example: two mirrors set at an angle of $120{}^\circ$ to one another. A ray of light is incident at $50{}^\circ$ on the first mirror. What is the angle of refraction $\theta_r$, with respect to a perpendicular line to the second mirror, as shown?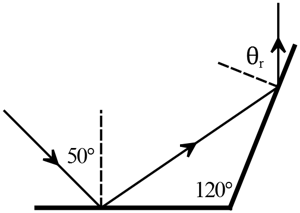 Two plane mirror intersect at some angle

Solution: By the law of reflection, the angle of incidence equals the angle of reflection, the reflected ray from the first incident on the horizontal mirror is at angle $50{}^\circ$.

In a triangle, the three interior angles always add up to $180{}^\circ$, so the reflected ray of the first mirror, which is served as the incident ray for the second mirror, strikes at an angle of $70{}^\circ$ with respect to the perpendicular line of the second mirror. Again using the law of reflection, the reflected ray from the latter mirror is $\theta_r=70{}^\circ$.

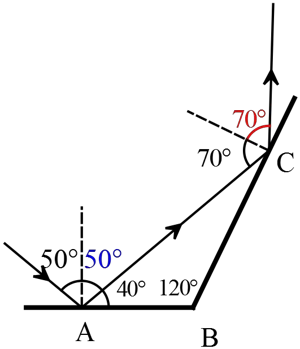
Solution intersection plane mirrors

Image properties in plane mirrors:

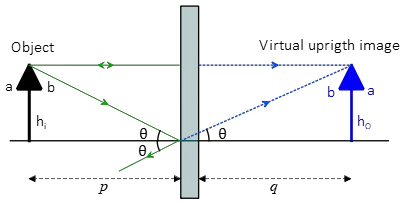
The following list is all properties of image formed in a plane mirror (All illustrated in the figure below)

The image distance $q$ is always equal to the object distance $p$ (proved above).
The image size $h_i$ is always equal to the object size $h_O$ i.e. $h_i=h_O$.
Image is always virtual (i.e. it is formed by the backward extension of the reflected rays behind the mirror) or Image and object lie on the opposite side of the flat mirror.
Image is always upright that is the upward direction of the tip of an arrow object is also upward in the image.
Image with respect to the object is always lateral inversion that is the right side of an object projected as a left side in the image (the object's right point $b$ is projected as image's left point $b$ in the figure below).

Illustration of image properties in plane mirror

Definition of lateral magnification:

In any image forming instruments, we can define a useful quantity which is the ratio of the image height $h_i$ to the object height $h_O$ and is called the lateral magnification $m$ \[m=\frac{\text{image height}}{\text{object height}}=\frac{h_i}{h_O}\]
The lateral magnification for a plane mirror is one ($m=1$) since the image height of an object in the plane mirror is the same size as the object i.e. $h_i=h_O$.

The above formula for lateral magnification is a general definition of any type of mirror or lens. We can extend the above magnification formula to include other mirrors as
\begin{align*} m \equiv \frac{\text{image height}}{\text{object height}}&=\frac{h_i}{h_O}\\\\ \text{Or}\\\\ m\equiv \frac{\text{image distance}}{\text{object distance}}&=-\frac{q}{p}\end{align*}To use this revised definition, we need some sign conventions to get the correct magnification size and sign.

Sign rule for the object distance: if the object is on the same side of the refracting or reflecting surface as the incoming light, then the object distance is positive $p>0$, otherwise, it is negative.
Sign rule for the image distance: when the image is on the same side of the refracting or reflecting surface (polished side) as the outgoing light, then the image distance is positive $q>0$, otherwise, it is negative.

Therefore, for plane mirrors, object and diverging light rays are on the same side of the mirror so the object distance is positive ($p>0$) but the image and outgoing (reflected) rays are on the opposite side of the mirror so the image distance is negative i.e. $q<0$ and proves that $m>0$

From the lateral magnification, we can deduce the orientation of the object’s image. When $m>0$, we say that the image is erect or upright. In the plane mirrors, we have always this case.

But there are situations (such as in the spherical mirror) in which the lateral magnifications are negative $m<0$. In these cases, the image is on the opposite side of the mirror (where the object does not exist) or the image is inverted.

Practice more problems: Mirrors and Lenses - Problems and solution

We end this course about plane mirrors in physics with the following question.

Which of the following statements are true for an image formed by a plane mirror?
(a) Image is sometimes erect.
(b) Image has sometimes apparent left-right reversal.
(c) Based on the position of the object, there is a situation where the image is real.
(d) Image has always a lateral magnification of one.

Answer: See the above section about properties of the plane mirror for the correct answer which is (d).

Last Update: 8/16/2020

Author: Ali Nemati