Concave Mirror: Problems with Answers for AP Physics 2
Here, using the mirror equation and magnification formula for curved mirrors a number of problems on the concave mirror are solved which is helpful for the AP Physics 2 exam.
We tried to illustrate all properties of the image formed by a concave mirror using equations and ray diagrams for a deeper understanding.
Summary of concave spherical mirrors
Mirror equation is \[\frac{1}{f}=\frac{1}{d_i}+\frac{1}{d_o}\] Where $f, d_i, d_o$ are the focal length, image distance and the object distance, respectively.
The magnification formula for spherical mirrors is also written as \[M=-\frac{d_i}{d_o}=\frac{h_i}{h_o}\] where $h_i, h_o$ are the image and object heights, respectively.
Sign Rules for Concave mirror:
- The focal length is positive $f>0$.
- The image distance must be inserted positive $d_i>0$ if the image is formed in front of the mirror.
- The image distance must be inserted negative $d_i<0$ if the image is formed back of the mirror.
Note: In front of the mirror is where the object is placed.
Concave Mirror Solved Problems:
Problem (1): A pencil is placed 6 cm in front of a concave mirror having a radius of curvature of 40 cm.
(a) What is its focal length?
(b) Determine the position of the image formed by this mirror.
(c) Draw a ray diagram and verify your previous results.
(d) What do we conclude from this problem?
Solution: (a) Recall that the focal length $f$ of a spherical mirror is related to the radius of curvature $R$ by the following formula \[f=\frac R2\] Substituting the known value into the above, we get \[f=\frac R2=\frac {40}{2}=20\quad {\rm cm}\]
(b) Using the mirror equation below and solving for unknowns such as image distance $d_i$ or object distance $d_o$, we complete our calculation. \[\frac{1}{d_i}+\frac{1}{d_o}=\frac{1}{f}\] To use mirror equation, we must note the sign rules involved in this equation:
- $f<0$ for convex mirror and $f>0$ for concave mirror.
- The image distance is always formed behind the convex mirror so $d_i<0$.
- In a concave mirror, if the image is formed on the same side of the object so $d_i>0$ otherwise $d_i<0$ must be inserted.
In this problem, the mirror is concave so focal length must be put with a plus sign $f>0$ in the mirror equation. \begin{align*} \frac{1}{f}&=\frac{1}{d_i}+\frac{1}{d_o}\\ \\ \frac{1}{20}&=\frac{1}{d_i}+\frac{1}{6}\\ \\ \Rightarrow \frac{1}{d_i}&=\frac{1}{20}-\frac{1}{6}\\\\&=\frac{6-20}{20\times 6}\\ \\ &=\frac{-14}{20\times 6}\end{align*} Flipping both sides of above relation, we get \[d_i=-\frac{120}{14}=8.57\quad {\rm cm}\] As you can see, we obtained a negative value for image distance for an object in front of a concave mirror. Thus, we conclude that the image must be formed on the opposite side of the mirror, or in other words, behind the mirror.
This image which is formed on the opposite side of the object is called a virtual image.
Therefore, the image of the above pencil is located about 9 cm behind the mirror.
(c) In the following figure, using two rays we obtained the image of the pencil.
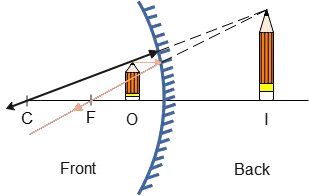
(d) In this problem, the object sits between the focal point and the concave mirror. As the ray diagram above showed, once there was such a case, we obtain a virtual, upright, and magnified image. But how much bigger? see next problem.
Problem (2): A candle 6 cm tall is placed at a distance of 8 cm in front of a concave mirror whose radius of curvature is 20 cm. Determine the position, size, orientation, and nature (real or virtual) of the image.
Solution: Known data is object' height $h_o=6\,{\rm cm}$, object distance $d_o=10\,{\rm cm}$, and the radius of curvature of the mirror $R=20\,{\rm cm}$. The focal length is obtained as below \[f=\frac R2=10\quad {\rm cm}\] As you can see, $d_o<f$ that is the object is located between the focal point and the concave mirror. In such cases, we have a virtual, upright, and bigger image (see the previous problem).
Applying the mirror equation get the position of the image $d_i$ as below \begin{align*} \frac{1}{f}&=\frac{1}{d_i}+\frac{1}{d_o}\\ \\ \frac{1}{10}&=\frac{1}{d_i}+\frac{1}{8}\\ \\ \Rightarrow \frac{1}{d_i}&=\frac{1}{10}-\frac{1}{8}\\\\&=\frac{8-10}{10\times 8}\\ \\ &=\frac{-2}{80}\end{align*} Reversing both sides of the above, we have $d_i=-40\,{\rm cm}$. Because image distance $d_i$ is negative, the image is on the opposite side of the mirror and hence is virtual.
To quantify how much bigger the image is in the curved mirrors, we use the magnification formula for curved mirrors as below \[M=\frac{h_i}{h_o}=-\frac{d_i}{d_o}\] Where $h_i$, $h_o$ are the image and object heights. \[M=-\frac{d_i}{d_o}=-\frac{-40}{8}=5\] Thus, the object is magnified as big as 5 times.
Problem (3): A certain concave spherical mirror has a focal length of 10 cm. An object is located 10 cm in front of it. Find the properties of the image.
Solution: Here, the object is at the focal point. Use the mirror equation to find the image position as below \begin{align*} \frac{1}{f}&=\frac{1}{d_i}+\frac{1}{d_o}\\ \\ \frac{1}{10}&=\frac{1}{d_i}+\frac{1}{10}\\ \\ \frac{1}{d_i}&=0 \\ \\ \Rightarrow d_i&=\infty \end{align*} Thus, the image is formed at infinity!. Using the magnification formula, we can see that it is also infinite.
From this problem, we conclude that when an object is placed at the focal point, its image is formed at infinity with infinite in size.
Problem (4): In front of a concave mirror whose radius of curvature is 20 cm we place a candle, 5 cm tall, at a distance of 25 cm away from it. Determine (a) the position,(b) the size, and (c) the nature (real or virtual) and orientation of the image.
Solution: All we need to find the image properties is to apply the mirror equation and magnification formula. In this problem, the radius of curvature of the concave curved mirror is given which is related to the focal length by the following formula \[f=\frac R2=\frac {20}{2}=10\,{\rm cm}\] The object is placed outside the center of the curvature of the concave mirror because $d_o>2f$. Now, we want to find the properties of the image formed by this object in this position.
(a) First of all, using the mirror equation we find the image distance from the concave mirror but recall that, according to mirror sign rules, for the concave mirror, the focal length must be inserted as $f>0$. \begin{align*} \frac{1}{f}&=\frac{1}{d_i}+\frac{1}{d_o}\\ \\ \frac{1}{10}&=\frac{1}{d_i}+\frac{1}{25}\\ \\ \frac{1}{d_i}&=\frac{1}{10}-\frac{1}{25}\\\\&=\frac{25-10}{10\times 25}\\\\&=\frac{15}{25} \\ \\ \Rightarrow d_i&=\frac{25}{15}=16.7\,{\rm cm} \end{align*} Because $d_i>0$, the image is in front of the mirror and is real (on the same side of the object). In other words, the image is formed between the focal point and the center of the curvature.
(b) Magnification in curved mirrors is the ratio of the image size to the object size or the ratio of the image distance to the object distance with a negative. \[M=\frac{h_i}{h_o}=-\frac{d_i}{d_o}\]
From the first expression, we can find the magnification of the mirror as \[M=-\frac{d_i}{d_o}=\frac{16.7}{25}=-0.6\] The image is 0.6 the size of the object.
The image height is also obtained by the second expression as below \begin{align*} M&=\frac{h_i}{h_o}\\\\ -0.6&=\frac{h_i}{5}\\\\ \Rightarrow h_i&=(-0.6)(5)=-3\,{\rm cm}\end{align*} The minus sign indicates that the image is inverted.
(c) Because $d_i>0$, the image is real. Since the magnification is negative $M<0$, the image is inverted.
All of the above findings can also be obtained by a concave mirror ray diagram as shown in the figure below.
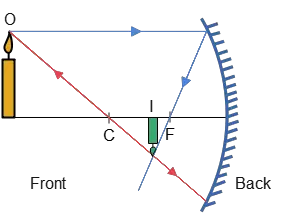
The notes we learn from this problem are that when an object is placed outside the center of curvature of a concave mirror, then the image is real, inverted, reduced in size, and is formed between focal point $f$ and center of curvature $C$.
For more practicing, you can also check out the following pages
Converging Lens Problems with Solution
Diverging Lens Problems with Solution
Author: Dr. Ali Nemati
Date Published: 5/14/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
