Spherical Mirrors: Definition, Solved Examples

One of the key properties of plane mirrors is that the object size is equal to the corresponding image size.

But there are mirrors that images formed by these are not equal to the object size. These mirrors are known as spherical mirrors or curved mirrors.

Spherical mirrors are a section cut out of a large spherical polished surface.

There are two types of spherical mirrors: concave and convex.

In the concave (convex) case, the outside (inner) of the mirror part is polished and reflecting.

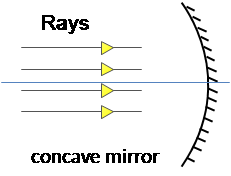
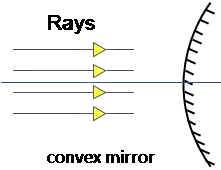
To study image formation by spherical mirrors, we need a few key concepts.

As illustrated in the figure below, the center of curvature of the mirror (the center of the sphere of which the mirror is a part of it) is at $C$ and the vertex of the mirror is at $V$.

The line joining the center of curvature to the vertex is called the optical (principal) axis.

The distance between $C$ and $V$ along the optical axis is the mirror's radius of curvature.

When a bundle of rays striking a concave mirror parallel to the optical axis, are reflected such that they come from the same point $f$ on the optical axis.

This point $f$ at which the parallel rays to the optical axis converge is called the focal point.

The distance from the vertex to the focal point is called focal length and is half of the radius of curvature $R$ i.e. $f=\frac{R}{2}$.

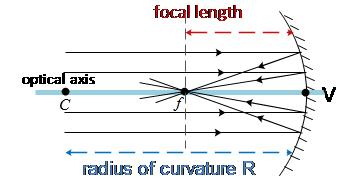
when the rays are too close and parallel to the principal axis they converge at the focal point $f$, in this case, we say that these rays are brought to a focus and are called the paraxial rays.

But if the rays diverging from the object are too far away from the optical axis they are brought to a focus ever closer to the mirror.

This lack of perfect focusing of a spherical mirror is called spherical aberration.

If a mirror has spherical aberration the image formed by it is blurred. The approximation in which we neglect the spherical aberration is called the paraxial approximation.

---

 

Parabolic Mirrors Definition

The parabolic mirror is a type of mirror in which the spherical aberration has been canceled. These mirrors are used to collect energy from a distant object such as incoming waves from a satellite or incoming starlight and bring them to a focal point.

The other commonplace application of these mirrors is in the car headlights. The car headlight consists of a light bulb that is placed at the focal point of a parabolic reflector.

According to the principles of reflection, when a point source (light bulb) is located at the focus, the rays emanating from it are reflected parallel to the optical axis.

---

 

Image formation by a spherical mirror

As shown in the figure, a bundle of rays from a point object $P$ reflects from a concave mirror and converges at point $P'$ (image point). Since the reflected rays actually pass through this point we say this image is called a real image.

By placing a photographic film at the image point we can take a photo from the object’s image.

This is in contrast to the virtual image formed by a plane mirror since in that case the image point is located behind the mirror and consequently no light rays actually emanate from it.

Thus real images are formed in front of the spherical mirrors.

To find the location of the image in the spherical mirrors by ray tracing, one must use the following special (principal) rays:

• The ray passing through the center of curvature is reflected on itself. From ordinary geometry, we know that these rays are perpendicular to the surface of the mirror. These rays are called Radial rays.
• The ray striking the mirror parallel to the principal axis reflects through the focal point $f$ (Parallel ray).
• The ray passing through the focal point is reflected parallel to the optical axis of the mirror (Focal ray)
• The ray striking the vertex of the mirror with a particular angle relative to the optical axis is reflected at the same angle as the incident ray. 

In the following figures, the different situations are shown for the concave mirror using ray diagrams.

Now use these special rays and find the location of images in different places of the object in a spherical mirror

•  If an extended object, say an arrow, is outside the center of curvature, its corresponding image is on the same side of the mirror (real image) as the incident rays and is larger and inverted as illustrated in the figure below.
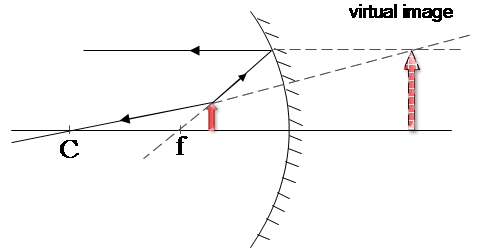
• When the object is placed inside the focal length, a virtual, erect, and larger image can be formed. As we can see, this image is located by the radial ray, which is reflected on itself, and the focal ray, which is reflected parallel to the optical axis. These reflected rays intersect each other at a point on the opposite side (behind) of the mirror. 
• If the object is between the center of curvature and the focal point, its image is real (on the same side as the incident rays), inverted, and larger.

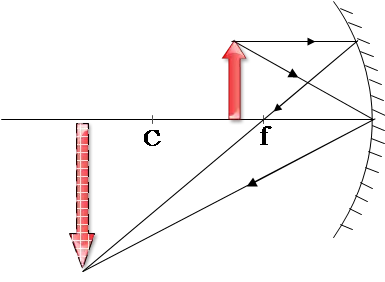
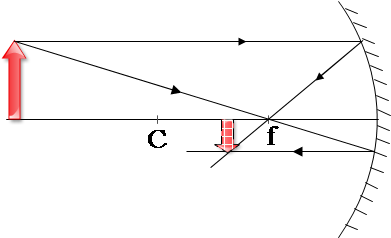
Using the geometrical arguments, we can find an equation that relates the object $s_o$ and image $s_i$ distances to the focal length $f$ of the spherical mirror. The mirror equation for curved mirrors is written below
\[\frac{1}{s_o} +\frac{1}{s_i}=\frac{1}{f}\]

Keep in mind that this equation is derived for paraxial rays and consequently is approximately correct.

The other important expression for the curved mirrors is the lateral magnification which is defined as the ratio of the image height $y_i$ to the object height $y_o$ or the ratio of the negative of image distance $s_i$ to the object distance $s_o$.
\[m=\frac{y_i}{y_o} =-\frac{s_i}{s_o}\]

The negative sign takes into account, as we can describe later since in the spherical mirrors the image and object can be on opposite sides of the mirror.

For plane mirrors, the radius of curvature is infinite. Thus the focal length is $f=\frac{R}{2}=\infty$. Using the mirror equation, we find $s_i=-s_o$, indicating that the image is behind the mirror at a distance equal to the object's distance.

Now by applying the lateral magnification equation, we can see that $m=+1$, indicating that the image is upright and the same size as the object, as we expected.

---

Sign Conventions for spherical mirrors

To apply the equation above, we must adopt a sign convention that is the same as the conventions for plane mirrors but for clarity, we have stated those for a spherical mirror as follows

• $s_o$ is positive if the object is on the incident-light side of the mirror. In this case, we say the object is real.
• $s_i$ is positive if the image is on the reflected-light side of the mirror. That is, we have a real image. 
• The radius of curvature $R$ (and thus the focal length $f$) is positive if the mirror is concave. 

If one of the above conventions does not satisfy that parameter must be negative.

 

Example Problem: the focal point of a concave mirror is 12 cm. Find the location and type of the image of an object that is placed on the optical axis in two following cases:
(a) At $20\,{\rm cm}$ in front of the mirror.
(b) At $4\,{\rm cm}$ in front of the mirror. 

Solution: (a) In this case, the object is placed between the focal point and the center of curvature. We expect its corresponding image must be real, inverted, larger, and formed outside the center of curvature. Using the mirror equation and applying the sign conventions, we have \begin{gather*} \frac{1}{s_o}+\frac{1}{s_i}=\frac{1}{f} \\ \\ \to \frac{1}{s_i}=\frac{1}{f}-\frac{1}{s_o} \\ \\ \Rightarrow \frac{1}{s_i}=\frac{1}{12}-\frac{1}{20}=\frac{5-3}{60}=\frac{1}{30}\\ \\ \Rightarrow s_i=+30\ {\rm cm}\end{gather*} As we can see the positive value of $s_i$ indicates that the image is real. Now by calculating the value of lateral magnification, we can observe the inverted image $m<0$. \[m=-\frac{s_i}{s_o}=-\frac{30}{20}=-1.5\]
(b) The object is placed inside the focal length, so use the mirror equation and lateral magnification to find the properties of the corresponding image.\begin{gather*} \frac{1}{s_o}+\frac{1}{s_i}=\frac{1}{f} \\ \\ \to \frac{1}{s_i}=\frac{1}{12}-\frac{1}{4}=\frac{1-3}{12}\\ \\ \Rightarrow s_i=-6\ {\rm cm}\end{gather*} Applying lateral magnification formula for curved mirrors, we get \[m=-\frac{s_i}{s_o}=-\frac{-6}{4}=+\frac{3}{2}\] Therefore, the image is formed behind the mirror (virtual since $s_i<0$) and is upright ($m>0$) and larger, as we expected.

Further Reading: 
Answered problems on the concave spherical mirror for AP physics

---

 

Convex mirrors

Up to now, all we said about curved mirrors were based on concave mirrors. There is another type of spherical mirror that is as important as concave mirrors. 

These mirrors which have the following properties are called convex mirrors. 

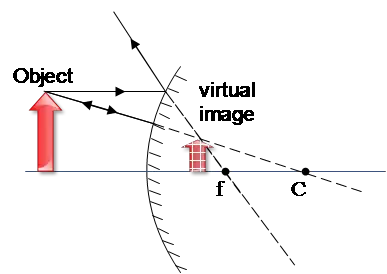
Images formed by a convex mirror is always virtual, upright, and smaller image.

A convex mirror never forms a real image of a real object.

The image is formed between the focal length and the vertex of the mirror as illustrated in the figure below.
Note: the focal length of this mirror is negative i.e. $f<0$

 

Example Problem (2): A candle 6 cm tall is placed 17 cm in front of a convex spherical mirror having a radius of curvature of 22 cm. 
(a) Draw a diagram and show the formation of the image. 
(b) Determine the position, size, orientation, and nature (real or virtual) of the image. 

Solution: (a) Ray diagram for the image formation of the candle in the convex spherical mirror is drawn below. 

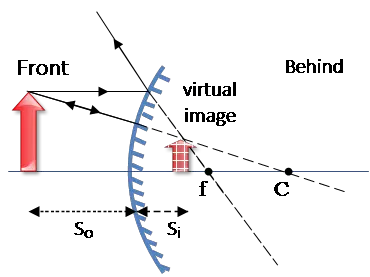
(b) To quantify the properties of the image formed above, first of all, we must recall the sign conventions for convex mirrors.

In the convex curved mirror, the image is formed behind the mirror where the focal length is, or in other words, on the opposite side of the object. In such curved mirrors, since the focal length and image location are behind the mirror so we adopt a negative for them in the mirror equation. Consequently, the mirror equation for a convex mirror is written as below \[\frac{1}{s_o}-\frac{1}{s_i}=-\frac{1}{f}\] Substituting the known values of object distance $s_o=0.17\,{\rm m}$ and the focal length $f=\frac r2=0.11\,{\rm m}$ into the convex mirror equation, we get \begin{align*} -\frac{1}{f}&=\frac{1}{s_o}-\frac{1}{s_i}\\ \\ -\frac{1}{0.11}&=\frac{1}{0.17}-\frac{1}{s_i}\\\\\Rightarrow \frac{1}{s_i}&=\frac{1}{0.17}+\frac{1}{0.11}=14.97 \\ \\\Rightarrow s_i&=6.68\,\quad {\rm cm}\end{align*} Thus, the image is formed about 6.68 cm behind the mirror. 

Now that we have the image and object distances, we can use the magnification formula \[M=\frac{h_i}{h_o}=-\frac{s_i}{s_o}\] to find the image size $h_i$ as below \begin{align*} \frac{h_i}{h_o}&=-\frac{s_i}{s_o} \\ \\ \frac{h_i}{6}&=-\frac{-6.68}{17} \\ \\ \Rightarrow h_i&=2.35\quad {\rm cm}\end{align*} As expected from the ray diagram in part (a). 

The object's orientation is clear from the ray diagram above as an erected image. There is another method to determine the image's orientation without drawing a ray diagram. 

Recall that in the curved mirrors, if we have $M>0$ then the image is formed as upright. Thus, we have \[M=-\frac{s_i}{s_o}=-\frac{-6.68}{17}>0\] As you can see, we obtained a positive magnification for this mirror so the image is erect.  

Note that, we must place a negative in front of the image distance $s_i$ in the magnification formula for the convex mirrors. 

Example Problem (3): A spherical mirror is used to form an image, five times as tall as an object, on a screen positioned 5 meters away from the mirror. 
(a) What type of curved mirror is used in this experiment?
(b) What is the location of the object relative to the mirror?
(c) Find the focal point of the unknown spherical mirror.

Solution: First list all known data as follows
magnification, which is defined as the negative of the ratio of the image distance to the object distance, was given as \[M=-\frac{s_i}{s_o}=\pm 5\] since the type of mirror is unknown, so we place a $\pm$ to incorporate both real and virtual images. 

The other data is the image distance from the unknown curved mirror, $s_i=5\,{\rm m}$. 

(a) From the magnification we can rule out the convex mirror with confidence, since as already said images in such mirrors are always smaller than the object.

(b) There are two situations in the concave mirror where the image size is larger than the object size. One is when the object is placed between the focal point and the concave mirror. The second is when the object is located between the center of curvature and the focal point.

In the first case, since the image is formed on the opposite side of the object we have a virtual image with negative image distance (see sign conventions above). 

In the second case, the larger image is formed on the same side of the object so, by definition, we have a real image with a positive image distance. 

In both cases above, according to the sign rules for curved mirrors, object distance, and focal length are positive. To find a positive object distance in the first case we must pick a positive sign for magnification in the magnification formula as below \begin{gather*} M=-\frac{s_i}{s_o} \\ \\ \to s_o=-\frac{s_i}{M} \\ \\ =-\frac{-5}{+5} \\ \\ \Rightarrow s_o=+1\,{\rm m}\end{gather*} Similarly for the second case, we must pick the negative sign for magnification to obtain a positive object distance as below \begin{gather*} M=-\frac{s_i}{s_o} \\ \\ \to s_o=-\frac{s_i}{M} \\ \\ =-\frac{+5}{-5} \\ \\ \Rightarrow s_o=+1\,{\rm m}\end{gather*} Therefore, the object is located 1 meter away from the concave mirror but where? we don't know until we have made a complete calculation (see below).

(c) Using mirror equation, $\frac{1}{s_i}+\frac{1}{s_o}=\frac{1}{f}$ where $s_i$ and $s_o$ are the image and object distances, and solving for the unknown focal length, we have \begin{align*} \frac{1}{f}&=\frac{1}{s_i}+\frac{1}{s_o} \\ \\ &=\frac{1}{+5}+\frac{1}{+1}\\\\&=\frac{6}{5}\\ \\ \Rightarrow f&=\frac 56=0.83\quad {\rm m}\end{align*} Note that in above if we chose a minus sign for image distance we get a negative for focal length which is a contradiction with the concave mirror. As a practice check this out. 

Further Reading: 
Converging Lens Problems with Solution
Diverging Lens Problems with Solution

---

Author: Ali Nemati
Last Modified: 5/10/2021