Average Acceleration: Solved Examples with Definition
In this article, some average acceleration worked examples are provided for high school physics.
Definition of Average Acceleration:
Objects move either with constant or varying velocities. For example, in everyday experience, you noticed when you step on the gas pedal of your car or brake one, the car's speed increases or decreases, Or in a turn your car's direction changes.
These changes in the magnitude of velocity or direction of a moving body, in physics, are described by acceleration.
In other words, the average acceleration is defined as the rate of change of the object's velocity and is given by the following formula:
\[\text{Average Acceleration}\equiv\frac{\text{change in velocity}}{\text{time elapsed}}\]
Typically average acceleration is denoted by $\bar a$ or $\vec{a}_{\text{ave}}$.
The units for acceleration are meters per squared second ($\rm \dfrac{m}{s^2}$).
Average Acceleration Examples:
Example (1): An automobile slows its speed from $25\,\rm m/s$ to $15\,\rm m/s$ in a time interval $2.5\,\rm s$, what is its acceleration?
Solution: the change in velocity of the automobile, $\Delta v=15-25=-10\,\rm m/s$, occurs in a time period of $\Delta t=2.5\,\rm s$. Thus, its average acceleration is found to be \[\bar{a}=\frac{-10}{2.5}=\boxed{-4\,\rm m/s^2}\] If we take the positive direction to be the right, then the average acceleration points to the left in the opposite direction to the velocity, meaning that the automobile has a slowing down motion. This is also an example of a decelerating motion.
One of the features of this motion is the moving object eventually comes to a rest or reverses its direction.
Keep in mind that the average acceleration is always in the same direction as the change in the velocity, but not always in the direction of the motion.
As you can see in this average acceleration example, the automobile is traveling to the right (the direction of the motion), but the direction of its average acceleration and change in velocity is toward the left.
Example (2): If a runner starts at rest and reaches a speed of $20\,\rm m/s$ in $2\,\rm s$, what is his average acceleration?
Solution: start at rest, so $v_1=0$, and finally reach a speed of $v_2=20\,\rm m/s$. Thus, the average acceleration is \[\bar{a}=\frac{20-0}{2}=\boxed{10\,\rm m/s^2}\] Assume the positive direction to be the right and the runner is moving in this direction. Its average acceleration is obtained positively, meaning the average acceleration is in the same direction as the motion.
Example (3): A car is accelerating from $20\,\rm m/s$ to rest in $1.0\,\rm s$. What is its average acceleration?
Solution: The initial and final velocities of the car, $v_1=20\,\rm m/s$ and $v_2=0$, in a time interval $1\,\rm s$ are given. Thus, the change in the car's velocity is $\Delta v=0-20=-20\,\rm m/s$.
According to the average acceleration formula, we have \[\bar{a}=\frac{-20}{1}=\boxed{-20\,\rm m/s^2}\] Assuming the positive direction to be the right and the car is moving toward this direction, the negative of average acceleration means that it points to the opposite direction of the motion. Thus, the car eventually will come to a stop, as expected.
Example (4): A car is traveling in a straight line along a highway at a constant speed of $80$ miles per hour for 10 seconds. Find its acceleration?
Solution: Average acceleration is a change in velocity divided by the time taken. Since the car's velocity (magnitude and direction) is constant over the entire course, so by definition of average acceleration, it is zero, i.e., $\bar{a}=0$.
Example (5): A plane has a take-off speed of $300\,{\rm \frac{km}{h}}$. What is the average acceleration (in $\rm \frac{m}{s^2}$) of the plane if the plane started from rest and took 45 seconds to take off?
Solution: Plane is initially at rest so $\vec{v_1}=0$ and its take off speed is $\vec{v_2}=300\,{\rm \frac{km}{h}}$. First off, convert ${\rm \frac{km}{h}}$ to SI units of velocity ${\rm \frac{m}{s}}$ as below\begin{align*} \rm{300\,\frac{km}{h}}&=\rm{300\,\frac{1000\,m}{3600\,s}}\\\\&=\rm{300\,\frac{1000}{3600}\,\frac{m}{s}}\\\\ &= \rm{83.4\,\frac{m}{s}} \end{align*} Now ratio of change in velocity, $\Delta \vec{v}=83.4\,{\rm \frac ms}$ over time elapsed $\Delta t=45\,\rm s$ is definition of average acceleration.\begin{align*} \bar{a}&=\frac{\Delta \vec{v}}{\Delta t} \\\\ &=\frac{83.4\,\rm{m/s}}{40\,{\rm s}}=2.085\,\rm{\frac{m}{s^2}} \end{align*}
Example (6): What average acceleration is needed to accelerate a car from $36\,{\rm \frac{km}{h}}$ to $72\,{\rm \frac{km}{h}}$ in $25$ seconds?
Solution: Initial and final velocities are $36\,{\rm \frac{km}{h}}$ and $72\,{\rm \frac{km}{h}}$, respectively. As before, convert them in SI units of the velocity as follows \begin{align*} \rm{\frac{km}{h}} &= \rm{\frac{1000\,m}{3600\,s}}\\ \\&= \rm{\frac{1000}{3600}\,\frac{m}{s}}\\\\ &= \rm{\frac{10}{36}\,\frac{m}{s}} \end{align*} In other words, multiply them by $\frac{10}{36}$. Then, $v_1=36\times\frac{10}{36}=10\,{\rm \frac ms}$ and $v_2=72\times\frac{10}{36}=20\,{\rm \frac ms}$. Now, by dividing the change of velocity, $\Delta v=20-10=10\,{\rm \frac ms}$ over the time elapsed $\Delta t=25\,{\rm s}$, we get the desired average acceleration \begin{align*} \bar{a}&=\frac{\Delta \vec{v}}{\Delta t} \\\\ &=\frac{20\,\rm{m/s}}{25\,{\rm s}}\\\\&=\boxed{0.8\,\rm m/s^2} \end{align*}
Example (7): Starting with a constant velocity of $50\,{\rm \frac{km}{h}}$, a car accelerates for 32 seconds at an acceleration of $0.5\,{\rm \frac{m}{s^2}}$. What is the velocity of the car at the end of the period of $32$ seconds of acceleration?
Solution: Here, the initial velocity, acceleration, and time interval over which this car accelerates are given, and the final velocity is requested. Therefore, using the definition of average acceleration we get, \begin{align*} \bar{a} &=\frac{\vec{v_2}-\vec{v_1}}{\Delta t} \\\\ 0.5 &= \frac{v_{2}-50\times\frac{10}{36}}{32}\\\\ 32\times 0.5 &= v_{2}-50\times\frac{10}{36}\\\\ \Rightarrow v_2 &=16+13.9=29.9\,\rm m/s \end{align*} For the second equality refer to Note $4$.
Example (8): A ball weighing $50\,\rm g$ with a speed of $25\,\rm m/s$ strike a wall and rebounds at $22\,\rm m/s$. Assuming the ball is in contact with the wall for $3.5\,\rm ms$, what is the magnitude of the average acceleration of the ball during this time interval?
Solution: Average acceleration is defined as the change in velocity divided by the time interval that this change occurs. Substituting the given numerical values into the average velocity formula get \begin{align*} \bar{a}&=\frac{v_2-v_1}{t_2-t_1}\\\\&=\frac{22-25}{3.5\times 10^{-3}} \\\\ &=\boxed{857.14\,\rm m/s^2} \end{align*} This is a very large acceleration.
Example (9): How long does it take to accelerate a car from a speed of $50\,{\rm \frac{km}{h}}$ to a speed of $100\,{\rm \frac{km}{h}}$ at a rate of $1\,{\rm \frac{m}{s^2}}$?
Solution: In this example, the unknown quantity is the time interval over which average acceleration occurs. Thus from definition of average acceleration along a straight line, we have \begin{align*} \bar{a} &=\frac{\vec{v_2}-\vec{v_1}}{\Delta t} \\\\ 1&=\frac{\left(100-50\right)\times \frac{10}{36}}{t}\\\\ \Rightarrow t&=\frac{\left(100-50\right)\times \frac{10}{36}}{1}\\\\ &=13.9\,{\rm s} \end{align*} In the second equality, kilometer/hour ($\rm km/h$) is converted into the meter/second ($\rm m/s$) by multiplying by $\frac{10}{36}$.
It is also possible to compute the acceleration of a moving object using a position versus time graph.
Example (10): A car start moving with a velocity of $-4\,{\rm m/s}$ from position $+4\,{\rm m}$. After $2\,{\rm s}$, its position is $-1\,{\rm m}$ with final velocity $-1\,{\rm m/s}$. Find:
(a) What is the displacement of the car?
(b) What is the average velocity of the car?
(c) What is the average acceleration of the car?
Solution:
(a) Displacement is defined as the change in position of an object \begin{align*}\Delta x&=x_2-x_1\\&=-1-4=-5\,{\rm m}\end{align*}
(b) Average velocity is $\bar{v}=\frac{\Delta x}{\Delta t}$ so \begin{align*}\bar{v}&=\frac{\Delta x}{\Delta t}\\\\ &=\frac{-5}{2}\\\\ &=-2.5\,{\rm m/s}\end{align*}
(c) By applying average acceleration formula $\bar{a}=\frac{\Delta v}{\Delta t}$, we get \begin{align*}\bar{a}&=\frac{\Delta v}{\Delta t}\\\\ &=\frac{-1-(-4)}{2} \\\\ &=+1.5\,{\rm m/s^2}\end{align*}In this example, the negatives of velocities indicates the car moves in the negative $x$ direction but the average acceleration is toward the positive $x$ direction. Consequently, the car is slowing down because $a.v<0$, so the motion is slowing down.
All these kinematics quantities are also found using a position vs. time graph.
Example (11): A $5-g$ ball is dropped from a height. It bounces off a brick wall at $10\,{\rm m/s}$ and rebounds at $8\,{\rm m/s}$. The ball is in contact with the wall for $2\,{\rm ms}$. Find the average acceleration of the ball during the contact time.
Solution: Let the positive direction be up so the given data are $v_1=-10\,{\rm m/s}$, $v_2=+8\,{\rm m/s}$ and $\Delta t=2\times 10^{-3}\,{\rm s}$ which we converted the milliseconds into seconds.
By applying average acceleration formula, we get \begin{align*}\bar{a}&=\frac{\Delta v}{\Delta t}\\\\&=\frac{v_2-v_1}{\Delta t}\\\\&=\frac{+8-(-10)}{2\times 10^{-3}}\\\\&=9\times 10^{3}\,{\rm m/s^2}\end{align*}
Example (12): A plastic bullet of $2\,{\rm g}$ from a rifle is fired at a brick wall. It strikes the wall with $20\,{\rm m/s}$ and returns at $18\,{\rm m/s}$. If the contact time of the ball with the wall is $3\,{\rm ms}$, what is the bullet's average acceleration?
Solution: suppose the positive direction is toward the positive $x$ direction. Thus, we have $v_1=+20\,{\rm m/s}$, $v_2=-18\,{\rm m/s}$ and $\Delta t=3\times 10^{-3}\,{\rm s}$. Therefore, the average acceleration definition gives \begin{align*}\bar{a}&=\frac{\Delta v}{\Delta t}\\\\&=\frac{v_2-v_1}{\Delta t}\\\\&=\frac{-18-(+20)}{3\times 10^{-3}}\\\\&=-12\times 10^{3}\,{\rm m/s^2}\end{align*} The minus sign of acceleration indicates its direction which is toward the negative $x$ axis.
Example (13): The velocity-time graph of a moving car along a straight path is shown below. Find its average acceleration during the first 2 seconds of motion.
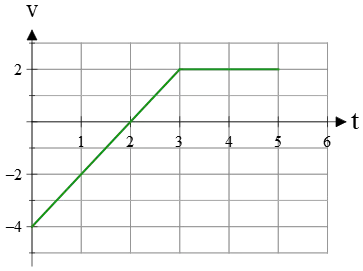
Solution: the slope of a line segment connecting two points on a velocity-time graph gives us the average acceleration.
The slope is also defined as the change in the vertical axis divided by a change in the horizontal axis. The starting point has coordinate $(v=-4\,{\rm m/s},t=0)$ and final point is $(v=0,t=2\,{\rm s})$. So, the slope of line joining these points is found as below \begin{align*}\text{slope=acceleration}&=\frac{\Delta x}{\Delta t}\\\\&=\frac{0-(-4)}{2-0}\\\\&=+2\quad {\rm m/s^2}\end{align*} Thus, the car increases its speed at a constant rate of $2\,{\rm m/s^2}$ in 2 s.
Average Acceleration Examples Tips:
Note $1$: Velocity is a vector quantity, meaning it has both a magnitude and a direction. If one of those changes over a period of time, then we have acceleration. Recall from uniform circular motion problems that an object with a uniform (constant) speed in a circular path can still have an acceleration like satellites around the Earth that move constantly but undergoes a type of acceleration called centripetal acceleration.
(On the page of vector practice problems, you can find how to calculate the magnitude and direction of a given vector)
Note $2$: Change in velocity is defined as the difference between initial ($\vec{v_1}$) and final ($\vec{v_2}$) velocities as below \[\Delta\vec{v}=\vec{v_2}-\vec{v_1}\]
Note $3$: If an object moves in a straight line since in this case there is no change in direction, the only part of the velocity vector changes is its magnitude. Thus, we can omit its direction sign, i.e., $\vec v=v$.
Note $4$: The average acceleration vector points in the same direction as the vector $\Delta \vec{v}$.
Summary:
According to vector definition in physics, velocity is a vector quantity with a magnitude and direction. If one of those changes during a finite period of time $\Delta t$, then we have average acceleration (vector) and is given by the following formula: \begin{align*} \vec{a}_\text{ave}&=\frac{\text{change in velocity vector}}{\text{elapsed time}}\\ &=\frac{\Delta \vec{v}}{\Delta t}\\ &=\frac{\vec{v}_2-\vec{v}_1}{t_2-t_1} \end{align*} SI unit of acceleration is meter per second per second ($m/s^2$) and its dimension is ${\rm L\,T^{-2}}$.
Practicing more problems on speed, velocity, and acceleration also helped a better understanding of the average acceleration concept.
Author: Dr. Ali Nemati
Last Update: Oct 1, 2022
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
