Definition of Vector in Physics with Solved Examples
Vector, in physics, is defined as any quantity that is described by both a number and a direction. Examples of a physical vector are displacement, velocity, and acceleration.
In contrast, there are quantities that are fully described merely by a number like distance, speed, temperature, time, and mass. These are called scalars.
Another definition of a vector in physics is a directed line segment in the plane (or space) which is constructed either by two arbitrary points or between the origin and another point somewhere with coordinate $B=(x,y)$ as shown in the figures below.
The ordered pair $(x,y)$ is called the components of the vector and the vector itself denoted by bold lowercase letters (such as $u$, $v$, $w$) or by an arrow or bar over a symbol (say, $\vec{u}$ or $\bar{u}$) for more convenient form when writing by hand.
Note: the length of a line segment is called the magnitude of a vector and the arrow at the endpoint indicates the direction of the vector.
Note: Any ordered triplet $(x,y,z)$, which is a list of three elements, both specify the location of a point in space and a vector in space.
Therefore, the vector constructed by two points $A=(x_1,y_1)$ and $B=(x_2,y_2)$ in the plane is as follows\[\vec{AB}=\left(x_2-x_1,y_2-y_1\right)\]
If your are getting ready for AP physics 1 exam, be sure check below:
AP Physics 1: vectors practice problems
Example Problem: Which of the following quantities are vectors in physics?
(a) 3 m , (b) 20 m/s due north, (c) 40 N at angle of $30^\circ$ with horizontal, (d) 3200 Calories, (e) 3 Amperes
Solution: Both options (b), (c) are defined as vectors in physics. There is no direction for any of the options (a), (d), and (e) so these are scalars in physics.
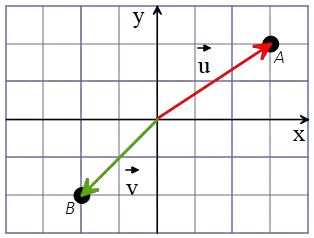
Example Problem : Given two vectors, $\vec{u}=(3,2)$ and $\vec{v}=(-2,-2)$. Using the definition of vector (in physics) as a directed line segment, draw those on a Cartesian coordinate.
Answer: when a vector is given in the form of an ordered pair $\vec{A}=(a,b)$, the numbers $a$ and $b$ indicates a point in the plane where the tail of the vector is placed at that location.
The two vectors above, are drawn in a graph paper as below.
Example Problem: In the following, some vector quantities in physics are described. Show graphically each vector in a graph paper.
(a) A 4.5-cm displacement vector that makes an angle of $122^\circ$ counterclockwise from $+x$ direction.
(b) A $12.2-{\rm m/s}$ velocity vector that makes an angle of $49^\circ$ clockwise from $-x$ direction.
Solution: The magnitude and direction of a physical vector are given, all things that are needed to draw a vector.
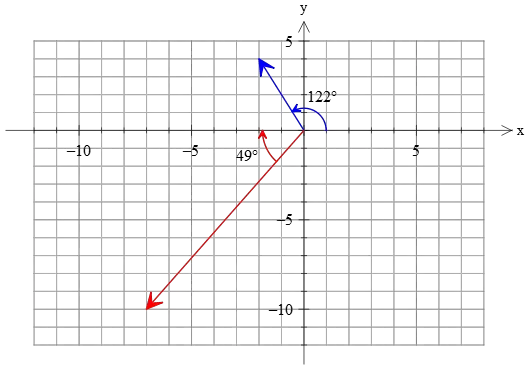
In the figures, pay attention to the angles from where they are measured.
Note that the displacement and velocity are representations of the definition of a vector in physics.
As you can see, all of these physical quantities make sense when either their direction and magnitude are known.
Magnitude of a vector:
The magnitude of the vector $\vec{A}$ with components $(A_x,A_y,A_z)$ is given by the following formula \[|\vec{A}|=\sqrt{A_x^2 + A_y^2 + A_z^2}\] where the magnitude is denoted by $|\ldots|$.
Example Problem: The components of a force vector in physics is specified as $F_x=9.8\,{\rm N}$ and $F_y=-6.4\,{\rm N}$. Find the magnitude of the given force vector.
Solution: First, write down the given components as an ordered pair like $\vec{F}=(9.8,-6.4)$. Now, by applying the above formula, we would have \[|\vec{F}|=\sqrt{(9.8)^2+(-6.4)^2}=11.7\quad {\rm N}\]
Direction of a vector:
Direction of the vector $\vec{A}=(A_x,A_y)$ (in plane) with respect to $+x$-axis in a counterclockwise direction is given by the formula below \[\tan \theta = \frac{\text{y-component}}{\text{x-component}}=\frac{A_y}{A_x}\] There are some things worth mentioning about this angle.
The angle that the above formula gives, is not always the correct angle. If the vector components are in the second and third quadrant, then the angle your calculator gives must be added to $180^\circ$.
Example Problem: The components of a displacement vector are $d_x=-86.6\,{\rm m}$ and $d_y=50\,{\rm m}$. Find the direction that the displacement vector makes with the positive $x$-axis.
Solution: substituting the components into the following formula gives \begin{align*} \theta &=\tan^{-1}\left(\frac{d_y}{d_x}\right)\\\\&=\tan^{-1}\left(\frac{50}{-86.6}\right)\\\\&=-30^\circ \end{align*} Because the components lie in the second quadrant so we must add $180^\circ$ to the given angle by calculator. \[\alpha=180^\circ+(-30^\circ)=150^\circ\] Hence, the displacement vector makes an angle of $150^\circ$ with $+x$-axis measured in a counterclockwise direction.
Unit Vector:
To indicate the direction of a vector in a plane or space, a new concept called a unit vector is used. The main features of unit vectors are as follows:
1) Its magnitude is unity irrespective of choice of coordinate system. In the other words, the vector $\vec{A}=(A_x,A_y,A_z)$ is a unit vector if and only if $|\vec{A}|=\sqrt{A_x^2 + A_y^2 +A_z^2}=1$.
2) It is a dimensionless quantity.
Example Problem: Consider the vector $\vec{A}=(a,a-1,a+1)$ be a unit vector. Find the value of $a$.
Answer: According to the definition of a unit vector, the magnitude of $\vec{A}$ must be unity, so we have \begin{align*}|\vec{A}|&=\sqrt{A_x^2 +A_y^2 + A_z^2}\\&=\sqrt{a^2 + (a-1)^2 +(a+1)^2}=1\\ & \Rightarrow \quad \sqrt{3a^2 + 2}=1\end{align*} Squaring both sides gives \begin{align*}3a^2 + 2 &=1\\3a^2 &=1 \\\Rightarrow a&=\pm\sqrt{\frac 1 3}\end{align*}
Note: There are an special unit vectors in the plane and the space along each of the coordinate axes which is shown in the figure. Those denoted as below \[ \hat{i}=(1,0,0) \ , \ \hat{j}=(0,1,0) \ , \ \hat{k}=(0,0,1)\]
Unit Vector Along an Arbitrary Vector
Once any vector is divided by its length, a unit vector in the same direction as the original vector is created.
In the other words, the unit vector $\hat{v}$ along the vector $\vec{v}$ is constructed by the following formula \[\hat{v}=\frac{\vec{v}}{|\vec{v}|}\]
Example Problem: Given the vector $\vec{OA}=(4,-3)$. Sketch the original vector and its unit vector.
Answer: Using the definition of a unit vector along an arbitrary vector, we must first calculate its length and then divide vector itself by its magnitude. \begin{align*}\text{vector magnitude}\quad |\overrightarrow{OA}|&=\sqrt{A_x^2 + A_y^2}\\&=\sqrt{4^2 + (-3)^2}\\&=5\end{align*}
Now we have, \begin{align*}\text{unit vector}\quad \widehat{OA}&=\frac{\overrightarrow {OA}}{|\overrightarrow {OA}|}\\\\&=\frac{(4,-3)}{5}\\\\ &=\left(\frac 45, \frac {-3}5\right)\end{align*}
Example Problem: let $\vec{a}=(-1,5,3)$. Find a unit vector in the same direction of $\vec{a}$.
Solution: The magnitude of any vector is computed as the square root of sum of its squared components. \[|\vec{a}|=\sqrt{(-1)^2 + 5^2 + 3^2}=\sqrt{35}\] The unit vector $\hat{a}$ in the same direction is constructed as below \begin{align*} \hat{a}&=\frac{\vec{a}}{|\vec{a}|}\\\\&=\frac{(-1\ ,5\ ,3)}{\sqrt{35}}\\\\&=\left(\frac{-1}{\sqrt{35}},\frac{5}{\sqrt{35}},\frac{3}{\sqrt{35}}\right) \end{align*}
Example Problem: Find a unit vector in the direction of the vector $\vec{v}=(2,-5)$.
Solution: The magnitude of the vector is $\sqrt{2^2 +(-5)^2}=\sqrt{29}$. Now divide vector itself by its magnitude to get a unit vector,$\hat{v}$, in the same direction. \begin{align*} \hat{v}&=\frac{\vec{v}}{|\vec{v}|}\\\\ &=\frac{(2,-5)}{\sqrt{29}}\\\\ &=\left(\frac{2}{\sqrt{29}},\frac{-5}{\sqrt{29}}\right) \end{align*} The unit vector is shown in the figure below in blue color.

You may also want to check out the following article about unit vectors in physics
Unit vectors with solved problems
Equal vectors:
Two vectors that have the same direction and the same magnitude are equal or equivalent. In the other words, two vectors $\vec{A}=(A_x,A_y)$ and $\vec{B}=(B_x,B_y)$ in the plane are equal if and only if their components are the same as follows \[ A_x=B_x \quad \text{and}\quad A_y=B_y\]
Example Problem of two equivalent vectors: Are vectors $\vec{u}$ and $\vec{w}$ equal?
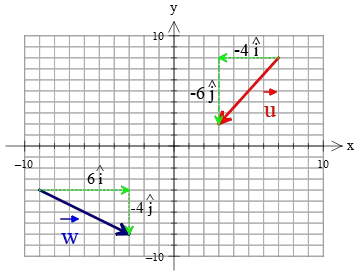
Solution: As you can see in the graph, because the two vectors are in different directions, so without any computation, we can deduce that the vectors are not equal or equivalent.
We can also prove this fact in detail as follows. First, using Pythagorean theorem find the magnitude of the vectors as below \begin{gather*} |\vec{u}|=\sqrt{(-4)^2+(-6)^2}=\sqrt{52}\\\\ |\vec{w}|=\sqrt{6^2+(-4)^2}=\sqrt{52}\end{gather*} As you can see, although the magnitude (size) of vectors are equal but each vector shows a different direction. Therefore, these vectors are not equal.
Operations On Vectors:
There are two quantities in physics. Vectors and scalars. Vectors are those that are completely specified with both a direction and a magnitude but scalars only with a number.
Vectors like scalars can be added or subtracted from each other or multiplied. To do these operations, we should learn some techniques.
Addition of vectors:
Consider two vectors with components $\vec{A}=(a_x,a_y)$ and $\vec{B}=(b_x,b_y)$ in a plane. The addition of two vectors, which is denoted by $\vec{A}+\vec{B}$, is another vector as $\vec{R}$ so that each of its components is determined as below \begin{align*} \vec{R}&=\vec{A}+\vec{B}\\&=(a_x+b_x \ ,\ a_y+b_y)\end{align*}
Note: The sum of vectors is also called the resultant vector or net vector.
Example Problem: You walk 3 km due north and then 4 km due west. Find (a) the resultant displacement in vector notation, (b) the angle of vector sum with the horizontal.
Solution: In physics displacement of an object due to the movement from one point to another point is defined as a vector sum of two (or any number) given vectors.
We are asked to find the displacement vector using components. First, write down each displacement as an individual vector as below \[\vec{d}_1=3\,\hat{j} \quad , \quad \vec{d}_2=4\,(-\hat{i})\] In the above, we used the definition of unit vectors along the $x$ and $y$ axes.
Note that in a plane, west corresponds to the negative $x$-axis whose unit vector is $-\hat{i}$.
(a) Let $\vec{d}$ be the resultant vector which is determined as below \begin{align*} \vec{d}&=\vec{d}_1+\vec{d}_2\\ &=3\,\hat{j} + 4\,(-\hat{i})\end{align*} Therefore, the displacement vector is obtained with components $\vec{d}=(-4\ , \ 3)$.
(b) The angle that a vector makes with the positive $x$-axis in a counterclockwise direction is found as below \begin{align*} \theta&=\tan^{-1}\left(\frac {d_y}{d_x}\right)\\\\&=\tan^{-1}\left(\frac{3}{-4}\right)\\\\&= -36.86^\circ\end{align*} Note that in finding the angle $\theta$ using the above formula, the angle given by your calculator is the right angle when the components of the vector lie in the first or fourth quadrant.
When the components lie in the second and third quadrant, the given angle (by your calculator) must be added to $180^\circ$ to get the correct answer.
In this problem, the components are in the second quadrant so the correct angle with the $+x$-direction is determined as below \[\alpha=-36.86^\circ+180^\circ=143.14^\circ\] Hence, the resultant displacement makes an angle of about $143^\circ$ counterclockwise from east.
In physics, this direction is also reading as $36^\circ$ north of west.
To find out more about the direction of a vector, practice these problems.
Properties of vector addition:
When two vectors are added together, the resultant vector has the following properties that can be proved by the algebra of components or graphically.
(1) \[\vec{A}+\vec{B}=\vec{B}+\vec{A}\]
(2) \[\vec{A}+(\vec{B}+\vec{C})=(\vec{A}+\vec{B})+\vec{C}\]
These properties tell us that the vector addition is commutative which means you can add vectors in any order you wish.
Not all vectors in physics obey this rule. Quantities like displacement and velocity respect this rule, but examples such as finite rotations in physics that do not obey this rule are not vectors.
Although rotations are fully described by a magnitude and a direction, finite rotations are not a vector and are examples of a scalar. In contrast, infinitesimal rotations about an arbitrary axis are vectors!
Geometric representation of vector addition:
To find the sum of two vectors (or any number), the following two methods can be used.
1) Triangle law for addition of two vectors:
If one constructs a triangle with the given two vectors so that the head of the second vector coincides with the tail of the first one, then the hypotenuse of this triangle is the sum of the two vectors.
This method is also called the tip-to-tail method.
2) Parallelogram Method:
Place the head of two vectors that coincide with each other. Then with these two vectors form a parallelogram. The sum of the two vectors is the diagonal of this parallelogram which is drawn from the origin to the tail of vectors as shown in the figure below.
Multiplication by a Scalar:
If $\vec{u}$ a vector and $k$ be a scalar (any number say, $2$,$-3$,...), then the multiplication of $k\vec{u}$ is a vector whose magnitude $k$ times greater and its direction depends on the sign of $k$.
If $k>0$ then $k\vec{u}$ is in the same direction of the original vector $\vec{u}$ and vice versa.
Example Problem: Find the magnitude and direction of the sum of vectors $2\vec{A}$ and $\vec{B}$.
Solution: Consider the components of the above vectors as $\vec{A}=(A_x,A_y)$ and $\vec{B}=(B_x,B_y)$. Thus, the magnitude of the resultant vector $\vec{C}=2\vec{A}+\vec{B}$ is obtained as \begin{align*} \vec{C}&=2\vec{A}+\vec{B}\\ &=2(A_x,A_y)+(B_x,B_y)\\&=(2A_x,2A_y)+(B_x,B_y)\\&=(2A_x+B_x , 2A_y+B_y)\end{align*} and its directions is defined as the ratio of $y$-component to the $x$-component, so \[\tan \theta = \frac{2A_y+B_y}{2A_x+B_x}\]
An example of a vector multiplied by a scalar in physics is force, $\vec{F}=m\vec{a}$, linear momentum, $\vec{p}=m\vec{v}$, and several other quantities.
Subtraction of Vectors:
The subtraction of two vectors $\vec{A}=(a_x,a_y)$ and $\vec{B}=(b_x,b_y)$ is given by the following formula \begin{align*}\vec{A}-\vec{B}&=\vec{A}+(-\vec{B})\\ &=(a_x-b_x,a_y-b_y) \end{align*}
As you can see, the difference between the two vectors does not have an independent definition.
Example Problem: In the following figure, two vectors $\vec{A}$ and $\vec{B}$ whose magnitudes are $A=5$ units and $B=2$ units are shown. Find the magnitude and direction of the $\vec{A}-\vec{B}$.
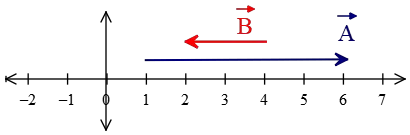
Answer: Recall that the definition of a vector in physics is a quantity that has both magnitude and direction.
In the problem, the magnitude of the vectors are given. Furthermore, in the figure, the directions are also specified. Combine all these information to construct, first, the vectors as below \[\vec{A}=5\,\hat{i} \quad ,\quad \vec{B}=2\,(-\hat{i})\] Now that the vectors are known in components, we can use the vector subtraction formula which yields \begin{align*}\vec{C}&=\vec{A}-\vec{B}\\&=5\,\hat{i}+2\,(-\hat{i})\\&=3\,\hat{i}\end{align*} Therefore, the difference vector is written as $\vec{C}=(3,0)$.
Scalar Multiplication:
There are situations in physics that a quantity is defined as a component of a vector in the direction of another vector. Work is an example of such definitions.
Remember that work is a scalar quantity in physics. Only a number completely specifies how much work is done by an object.
We also know that work is defined as the force component along the direction of an object's displacement. In this definition, two vectors are multiplied with each other and produce a scalar. But how?
The combination of magnitudes of two vectors and the cosine of the angle between them is called the scalar product of the vectors. This particular kind of multiplication of vectors in physics is written as $\vec{A}\cdot\vec{B}$ for two general vectors $\vec{A}$ and $\vec{B}$ and is defined by \[\vec{A}\cdot\vec{B}=|\vec{A}||\vec{B}|\cos\theta\] This product is also known as dot product.
Let the two vectors $\vec{A}=(a_x,a_y)$ and $\vec{B}=(b_x,b_y)$ are given. The scalar product between them is found as below formula \[\vec{A}\cdot\vec{B}=a_x b_x+a_y b_y\]
In Cartesian coordinate, the scalar product of two unit vectors are computed as below \begin{gather*} \hat{i}\cdot\hat{j}=\hat{k}\\\hat{j}\cdot\hat{k}=\hat{i}\\ \hat{k}\cdot\hat{i}=\hat{j}\end{gather*}
Example Problem: find the dot product of the following vectors.
(a) $\vec{A}=3\hat{i}-4\hat{j}$ and $\vec{B}=-4\hat{i}+2\hat{j}$
(b) $\vec{A}=3\hat{j}-2\hat{k}$ and $\vec{B}=2\hat{i}+\hat{j}$
Solution: Here, only the components of vectors are given so we can use the following formula.
(a) First, write each vector in a ordered pair as $\vec{A}=(3,-4,0)$ and $\vec{B}=(-4,2,0)$. Therefore, we have \begin{align*}\vec{A}\cdot\vec{B}&=a_x b_x+a_y b_y +a_z b_z\\&=(3)(-4)+(-4)(2)+0\\&=-20\end{align*}
(b) In a similar manner, $\vec{A}=(0,3,-2)$ and $\vec{B}=(2,1,0)$. \begin{align*}\vec{A}\cdot\vec{B}&=a_x b_x+a_y b_y +a_z b_z\\&=(0)(2)+(3)(1)+(-2)(0)\\&=3\end{align*}
Vector Multiplication:
There is another type of multiplication of two vectors that produces another vector. One of the prime examples, in physics, is torque.
Mathematically, the vector product of two vectors $\vec{A}$ and $\vec{B}$ is defined to be a vector $\vec{C}$ whose magnitude is a combination of magnitudes of the vectors and the sine of the angle between their direction.
The direction of vector cross product is found using the right-hand rule which is always a vector perpendicular to the plane of multiplied vectors.
This product symbolically is shown as $\vec{A}\times \vec{B}$ and for this reason, this is also known as the cross product.
Therefore, the cross product of two general vectors are defined as below \[\vec{A}\times\vec{B}=|\vec{A}||\vec{B}|\sin\theta\] In Cartesian coordinate, the cross product of unit vectors are given by \begin{align*}\hat{i}\times\hat{j}&=\hat{k} \\ \hat{j}\times\hat{k}&=\hat{i}\\\hat{k}\times\hat{i}&=\hat{j}\end{align*}
Example Problem: given two vectors $\vec{A}=2\hat{i}-3\hat{k}$ and $\vec{B}=\hat{j}+2\hat{k}$. Find $\vec{A}\times\vec{B}$.
Solution: \begin{align*}\vec{A}\times\vec{B}&=(2\hat{i}-3\hat{k})\times(\hat{j}+2\hat{k})\\\\&=2\,\underbrace{\hat{i}\times\hat{j}}_{\hat{k}}+4\,\underbrace{\hat{i}\times\hat{k}}_{-\hat{j}}\\\\&-3\,\underbrace{\hat{k}\times\hat{j}}_{-\hat{i}}-6\,\underbrace{\hat{k}\times\hat{k}}_{0}\\\\&=3\hat{i}-4\hat{j}+2\hat{k}\end{align*} As you can see, the cross product of the two given vectors is another vector.
Note that the division of a vector by a vector is not defined.
Summary:
In this long article, we presented a concise definition of a vector in physics along with numerous solved problems.
In physics, vectors have a well-defined magnitude and direction but scalars describe only by a number.
For practicing more problems about vectors, you can also see the page below
Practice problems on vectors for high schools
Author: Dr. Ali Nemati
Date Published: 8-2-2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
